北师大版七年级数学下册1.5平方差公式一课一练习题(Word版,含答案)
文档属性
| 名称 | 北师大版七年级数学下册1.5平方差公式一课一练习题(Word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 312.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-09 22:19:54 | ||
图片预览

文档简介
1.5《平方差公式》习题
一、选择题
1.下列各式不能运用平方差公式计算的是(
)
A.
B.
C.
D.
2.下列各式中,不能运用平方差公式计算的是(
)
A.
B.
C.
D.
3.下列各式中,不能用平方差公式计算的是(
)
A.B.
C.D.
4.能用平方差公式计算的是(
)
A.
B.
C.
D.
5.下列各式不能用平方差公式计算的是(
)
A.
B.
C.
D.
6.下列各多项式相乘:①(-2ab+5x)(5x+2ab);②(ax-y)(-ax-y);③(-ab-c)(ab-c);④(m+n)(-m-n).其中可以用平方差公式的有
(
)
A.4个
B.3个
C.2个
D.1个
7.下列乘法运算中不能用平方差公式计算的是(
)
A.(x+1)(x﹣1)
B.(x+1)(﹣x+1)
C.(﹣x+1)(﹣x﹣1)
D.(x+1)(﹣x﹣1)
8.若,则代数式的值为(
)
A.1
B.2
C.4
D.6
9.计算的正确结果是(
)
A.
B.
C.
D.
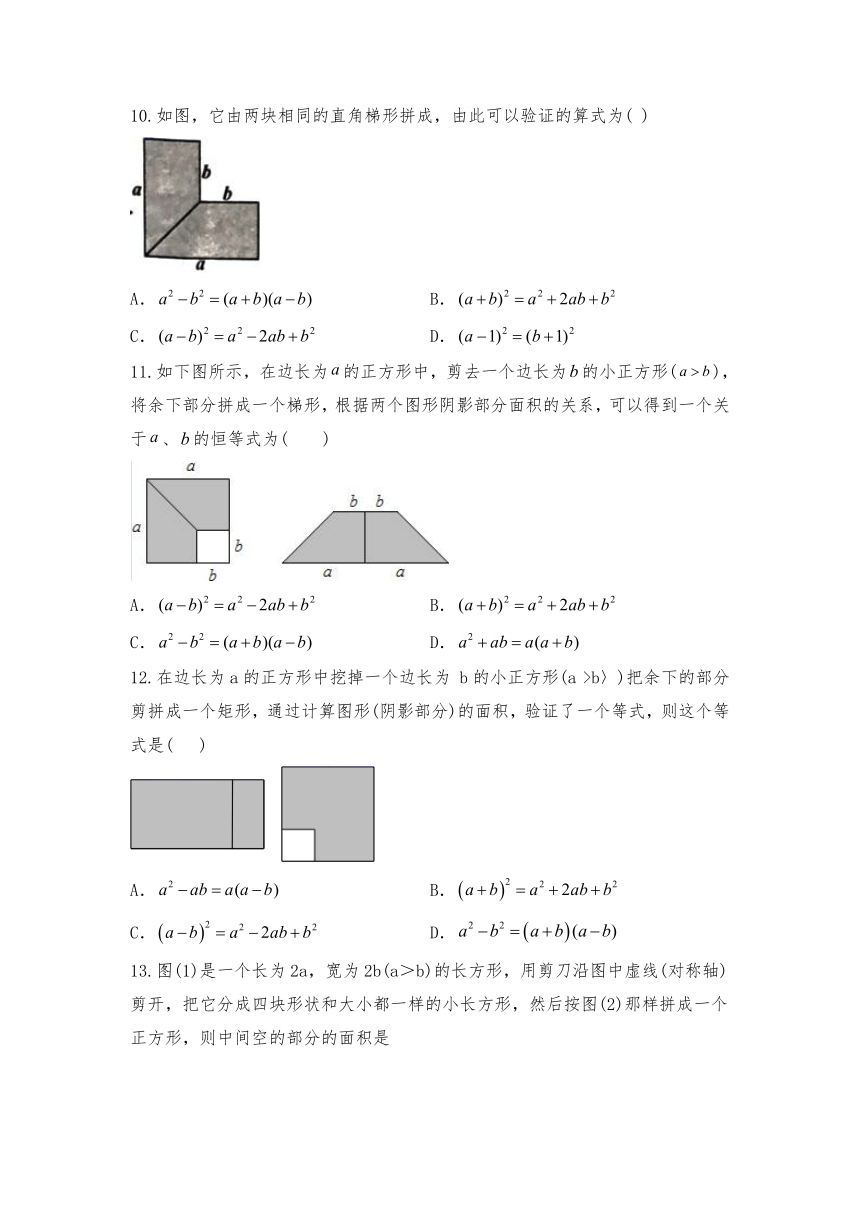
10.如图,它由两块相同的直角梯形拼成,由此可以验证的算式为(
)
A.
B.
C.
D.
11.如下图所示,在边长为的正方形中,剪去一个边长为的小正方形(),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于、的恒等式为(
)
A.
B.
C.
D.
12.在边长为a的正方形中挖掉一个边长为
b的小正方形(a
>b〉)把余下的部分剪拼成一个矩形,通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是(
)
A.
B.
C.
D.
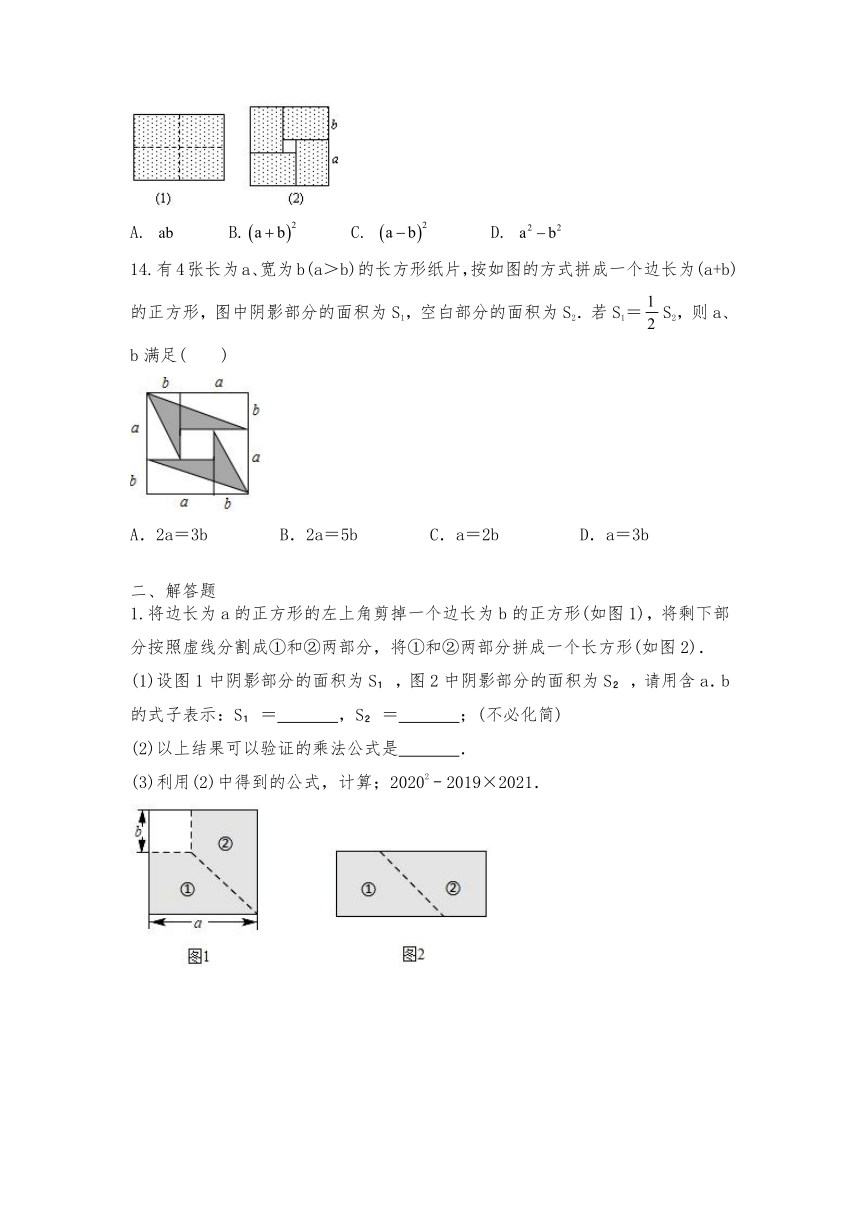
13.图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是
A.
B.
C.
D.
14.有4张长为a、宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中阴影部分的面积为S1,空白部分的面积为S2.若S1=S2,则a、b满足(
)
A.2a=3b
B.2a=5b
C.a=2b
D.a=3b
二、解答题
1.将边长为a的正方形的左上角剪掉一个边长为b的正方形(如图1),将剩下部分按照虚线分割成①和②两部分,将①和②两部分拼成一个长方形(如图2).
(1)设图1中阴影部分的面积为S?,图2中阴影部分的面积为S?,请用含a.b的式子表示:S?=
,S?=
;(不必化简)
(2)以上结果可以验证的乘法公式是
.
(3)利用(2)中得到的公式,计算;20202﹣2019×2021.
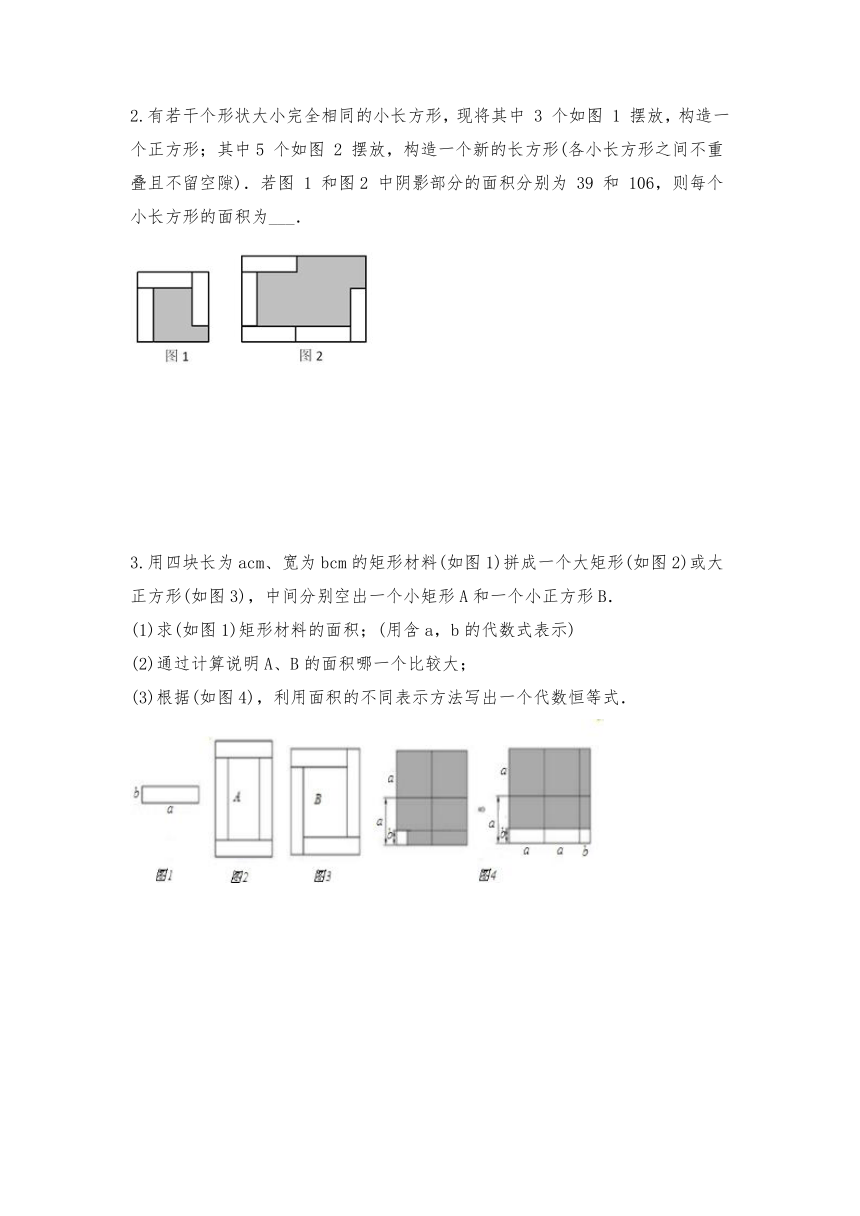
2.有若干个形状大小完全相同的小长方形,现将其中
3
个如图
1
摆放,构造一个正方形;其中5
个如图
2
摆放,构造一个新的长方形(各小长方形之间不重叠且不留空隙).若图
1
和图2
中阴影部分的面积分别为
39
和
106,则每个小长方形的面积为___.
3.用四块长为acm、宽为bcm的矩形材料(如图1)拼成一个大矩形(如图2)或大正方形(如图3),中间分别空出一个小矩形A和一个小正方形B.
(1)求(如图1)矩形材料的面积;(用含a,b的代数式表示)
(2)通过计算说明A、B的面积哪一个比较大;
(3)根据(如图4),利用面积的不同表示方法写出一个代数恒等式.
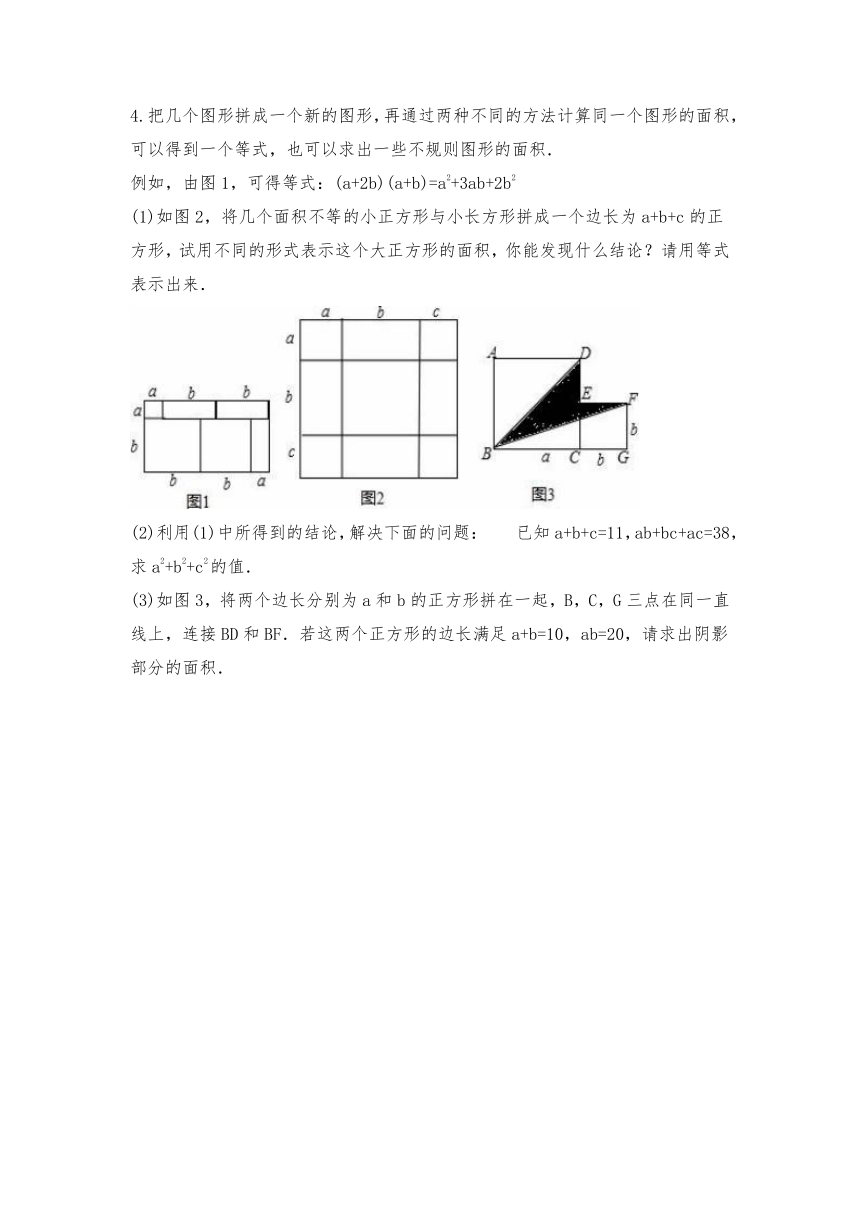
4.把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如,由图1,可得等式:(a+2b)(a+b)=a2+3ab+2b2
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来.
(2)利用(1)中所得到的结论,解决下面的问题:
已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=10,ab=20,请求出阴影部分的面积.
5.图1和图2的大正方形都是由一些长方形和小正方形组成的.观察图形,完成下列各题:
(1)如图1,求S大正方形的方法有两种:S大正方形=(x+y)2,同时,S大正方形=S①+S②+S③+S④=
.所以图1可以用来解释等式:
;同理图2可以用来解释等式:
.
(2)已知a+b+c=6,ab+bc+ca=11,利用上面得到的等式,求a2+b2+c2的值.
6.若x满足(x-4)
(x-9)=6,求(x-4)2+(x-9)2的值.
解:设x-4=a,x-9=b,则(x-4)(x-9)=ab=6,a-b=(x-4)-(x-9)=5,
∴(x-4)2+(x-9)2=a2+b2=(a-b)2+2ab=52+2×6=37
请仿照上面的方法求解下面问题:
(1)若x满足(x-2)(x-5)=10,求(x-2)2
+
(x-5)2的值
(2)已知正方形ABCD的边长为x,E,F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是15,分别以MF、DF作正方形,求阴影部分的面积.
7.(阅读材料)
我们知道,图形也是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系,而运用代数思想也能巧妙地解决一些图形问题.
在一次数学活动课上,张老师准备了若干张如图1所示的甲、乙、丙三种纸片,其中甲种纸片是边长为的正方形,乙种纸片是边长为的正方形,丙种纸片是长为,宽为的长方形,并用甲种纸片一张,乙种纸片一张,丙种纸片两张拼成了如图2所示的一个大正方形.
(理解应用)
(1)观察图2,用两种不同方式表示阴影部分的面积可得到一个等式,请你直接写出这个等式.
(拓展升华)
(2)利用(1)中的等式解决下列问题.
①已知,,求的值;
②已知,求的值.
8.某同学利用若干张正方形纸片进行以下操作:
(1)从边长为a的正方形纸片中减去一个边长为b的小正方形,如图1,再沿线段AB把纸片剪开,最后把剪成的两张纸片拼成如图2的等腰梯形,这一过程所揭示的公式是________.
(2)先剪出一个边长为a的正方形纸片和一个边长为b的正方形纸片,再剪出两张边长分别为a和b的长方形纸片,如图3,最后把剪成的四张纸片拼成如图4的正方形.这一过程你能发现什么代数公式?
答案
一、选择题
1.C.2.C.3.B.4.B.5.A.6.B.7.D.
8.D.9.B.10.A.11.C.12.D.13.C.14.C.
二、解答题
1.解:(1)根据图形以及正方形和长方形的面积计算公式可得:S?=a2﹣b2,S?=(a+b)(a﹣b)
故答案为:a2﹣b2,(a+b)(a﹣b);
(2)以上结果可以验证的乘法公式是a2﹣b2=(a+b)(a﹣b).
故答案为:(a+b)(a﹣b)=a2﹣b2.
(3)20202﹣2019×2021
=20202﹣(2020﹣1)×(2020+1)
=20202﹣(20202﹣1)
=20202﹣20202+1
=1.
2.解:设小长方形的长为a,宽为b,
在图1中,有:(a+b)2-3ab=39,
在图2中,有:(a+2b)(2a+b)-5ab=106,
分别整理得:a2+b2-ab=39,a2+b2=53,
将a2+b2=53代入a2+b2-ab=39中,
解得:ab=14,
故每个小长方形的面积为14,
故答案为:14.
3.(1)S=长×宽=ab;
(2)根据图形可得:矩形的长=(2b+a),宽=a;正方形的边长=a+b,
矩形的面积=2ab+a2,正方形的面积=a2+2ab+b2,
正方形面积-矩形的面积=b2,
∴矩形的面积大;
(3)根据图形可得:a2-b2=(a-b)(a+b).
4.(1)(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;
(2)∵a+b+c=11,ab+bc+ac=38,
∴a2+b2+c2
=(a+b+c)2﹣2(ab+ac+bc)=121﹣76=45;
(3)∵a+b=10,ab=20,
∴S阴影=a2+b2﹣(a+b)?b﹣a2
=a2+b2﹣ab
=(a+b)2﹣ab
=×102﹣×20
=50﹣30
=20.
5.(1)∵S③=S④=xy,S①=x2,S②=y2,
∴S大正方形=S①+S②+S③+S④=x2+2xy+y2.
∴(x+y)2=x2+2xy+y2.
∵图2大正方形的面积=(a+b+c)2,
同时图2大正方形的面积=a2+b2+c2+2ab+2ac+2bc;
∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
故答案为:x2+2xy+y2,(x+y)2=x2+2xy+y2,(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(2)∵(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,
∴a2+b2+c2=(a+b+c)2﹣2ab﹣2ac﹣2bc
=(a+b+c)2﹣2(ab+ac+bc)
=62﹣2×11
=14.
6.(1)设,,则,
∴
(2)根据题意可知正方形ABCD的边长为x,
∵EMFD是长方形,
∴MF=ED,
∴
,
,
设,,
则S长方形EMFD=,,
,得
∵S阴影部分=MF2-DF2,
即S阴影部分=
故阴影部分的面积是16.
7.(1).
(2)①由题意得:,
把,代入上式得:
.
②由题意得:
.
8.(1)图1的面积为a2-b2,图2的面积为
,
∴根据图1和图2的面积相等可得到;
(2)拼图前的面积为,拼图后的面积为,
因此可得;
(3)能拼成长方形.
等式:.
一、选择题
1.下列各式不能运用平方差公式计算的是(
)
A.
B.
C.
D.
2.下列各式中,不能运用平方差公式计算的是(
)
A.
B.
C.
D.
3.下列各式中,不能用平方差公式计算的是(
)
A.B.
C.D.
4.能用平方差公式计算的是(
)
A.
B.
C.
D.
5.下列各式不能用平方差公式计算的是(
)
A.
B.
C.
D.
6.下列各多项式相乘:①(-2ab+5x)(5x+2ab);②(ax-y)(-ax-y);③(-ab-c)(ab-c);④(m+n)(-m-n).其中可以用平方差公式的有
(
)
A.4个
B.3个
C.2个
D.1个
7.下列乘法运算中不能用平方差公式计算的是(
)
A.(x+1)(x﹣1)
B.(x+1)(﹣x+1)
C.(﹣x+1)(﹣x﹣1)
D.(x+1)(﹣x﹣1)
8.若,则代数式的值为(
)
A.1
B.2
C.4
D.6
9.计算的正确结果是(
)
A.
B.
C.
D.
10.如图,它由两块相同的直角梯形拼成,由此可以验证的算式为(
)
A.
B.
C.
D.
11.如下图所示,在边长为的正方形中,剪去一个边长为的小正方形(),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于、的恒等式为(
)
A.
B.
C.
D.
12.在边长为a的正方形中挖掉一个边长为
b的小正方形(a
>b〉)把余下的部分剪拼成一个矩形,通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是(
)
A.
B.
C.
D.
13.图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是
A.
B.
C.
D.
14.有4张长为a、宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中阴影部分的面积为S1,空白部分的面积为S2.若S1=S2,则a、b满足(
)
A.2a=3b
B.2a=5b
C.a=2b
D.a=3b
二、解答题
1.将边长为a的正方形的左上角剪掉一个边长为b的正方形(如图1),将剩下部分按照虚线分割成①和②两部分,将①和②两部分拼成一个长方形(如图2).
(1)设图1中阴影部分的面积为S?,图2中阴影部分的面积为S?,请用含a.b的式子表示:S?=
,S?=
;(不必化简)
(2)以上结果可以验证的乘法公式是
.
(3)利用(2)中得到的公式,计算;20202﹣2019×2021.
2.有若干个形状大小完全相同的小长方形,现将其中
3
个如图
1
摆放,构造一个正方形;其中5
个如图
2
摆放,构造一个新的长方形(各小长方形之间不重叠且不留空隙).若图
1
和图2
中阴影部分的面积分别为
39
和
106,则每个小长方形的面积为___.
3.用四块长为acm、宽为bcm的矩形材料(如图1)拼成一个大矩形(如图2)或大正方形(如图3),中间分别空出一个小矩形A和一个小正方形B.
(1)求(如图1)矩形材料的面积;(用含a,b的代数式表示)
(2)通过计算说明A、B的面积哪一个比较大;
(3)根据(如图4),利用面积的不同表示方法写出一个代数恒等式.
4.把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如,由图1,可得等式:(a+2b)(a+b)=a2+3ab+2b2
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来.
(2)利用(1)中所得到的结论,解决下面的问题:
已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=10,ab=20,请求出阴影部分的面积.
5.图1和图2的大正方形都是由一些长方形和小正方形组成的.观察图形,完成下列各题:
(1)如图1,求S大正方形的方法有两种:S大正方形=(x+y)2,同时,S大正方形=S①+S②+S③+S④=
.所以图1可以用来解释等式:
;同理图2可以用来解释等式:
.
(2)已知a+b+c=6,ab+bc+ca=11,利用上面得到的等式,求a2+b2+c2的值.
6.若x满足(x-4)
(x-9)=6,求(x-4)2+(x-9)2的值.
解:设x-4=a,x-9=b,则(x-4)(x-9)=ab=6,a-b=(x-4)-(x-9)=5,
∴(x-4)2+(x-9)2=a2+b2=(a-b)2+2ab=52+2×6=37
请仿照上面的方法求解下面问题:
(1)若x满足(x-2)(x-5)=10,求(x-2)2
+
(x-5)2的值
(2)已知正方形ABCD的边长为x,E,F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是15,分别以MF、DF作正方形,求阴影部分的面积.
7.(阅读材料)
我们知道,图形也是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系,而运用代数思想也能巧妙地解决一些图形问题.
在一次数学活动课上,张老师准备了若干张如图1所示的甲、乙、丙三种纸片,其中甲种纸片是边长为的正方形,乙种纸片是边长为的正方形,丙种纸片是长为,宽为的长方形,并用甲种纸片一张,乙种纸片一张,丙种纸片两张拼成了如图2所示的一个大正方形.
(理解应用)
(1)观察图2,用两种不同方式表示阴影部分的面积可得到一个等式,请你直接写出这个等式.
(拓展升华)
(2)利用(1)中的等式解决下列问题.
①已知,,求的值;
②已知,求的值.
8.某同学利用若干张正方形纸片进行以下操作:
(1)从边长为a的正方形纸片中减去一个边长为b的小正方形,如图1,再沿线段AB把纸片剪开,最后把剪成的两张纸片拼成如图2的等腰梯形,这一过程所揭示的公式是________.
(2)先剪出一个边长为a的正方形纸片和一个边长为b的正方形纸片,再剪出两张边长分别为a和b的长方形纸片,如图3,最后把剪成的四张纸片拼成如图4的正方形.这一过程你能发现什么代数公式?
答案
一、选择题
1.C.2.C.3.B.4.B.5.A.6.B.7.D.
8.D.9.B.10.A.11.C.12.D.13.C.14.C.
二、解答题
1.解:(1)根据图形以及正方形和长方形的面积计算公式可得:S?=a2﹣b2,S?=(a+b)(a﹣b)
故答案为:a2﹣b2,(a+b)(a﹣b);
(2)以上结果可以验证的乘法公式是a2﹣b2=(a+b)(a﹣b).
故答案为:(a+b)(a﹣b)=a2﹣b2.
(3)20202﹣2019×2021
=20202﹣(2020﹣1)×(2020+1)
=20202﹣(20202﹣1)
=20202﹣20202+1
=1.
2.解:设小长方形的长为a,宽为b,
在图1中,有:(a+b)2-3ab=39,
在图2中,有:(a+2b)(2a+b)-5ab=106,
分别整理得:a2+b2-ab=39,a2+b2=53,
将a2+b2=53代入a2+b2-ab=39中,
解得:ab=14,
故每个小长方形的面积为14,
故答案为:14.
3.(1)S=长×宽=ab;
(2)根据图形可得:矩形的长=(2b+a),宽=a;正方形的边长=a+b,
矩形的面积=2ab+a2,正方形的面积=a2+2ab+b2,
正方形面积-矩形的面积=b2,
∴矩形的面积大;
(3)根据图形可得:a2-b2=(a-b)(a+b).
4.(1)(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;
(2)∵a+b+c=11,ab+bc+ac=38,
∴a2+b2+c2
=(a+b+c)2﹣2(ab+ac+bc)=121﹣76=45;
(3)∵a+b=10,ab=20,
∴S阴影=a2+b2﹣(a+b)?b﹣a2
=a2+b2﹣ab
=(a+b)2﹣ab
=×102﹣×20
=50﹣30
=20.
5.(1)∵S③=S④=xy,S①=x2,S②=y2,
∴S大正方形=S①+S②+S③+S④=x2+2xy+y2.
∴(x+y)2=x2+2xy+y2.
∵图2大正方形的面积=(a+b+c)2,
同时图2大正方形的面积=a2+b2+c2+2ab+2ac+2bc;
∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
故答案为:x2+2xy+y2,(x+y)2=x2+2xy+y2,(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(2)∵(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,
∴a2+b2+c2=(a+b+c)2﹣2ab﹣2ac﹣2bc
=(a+b+c)2﹣2(ab+ac+bc)
=62﹣2×11
=14.
6.(1)设,,则,
∴
(2)根据题意可知正方形ABCD的边长为x,
∵EMFD是长方形,
∴MF=ED,
∴
,
,
设,,
则S长方形EMFD=,,
,得
∵S阴影部分=MF2-DF2,
即S阴影部分=
故阴影部分的面积是16.
7.(1).
(2)①由题意得:,
把,代入上式得:
.
②由题意得:
.
8.(1)图1的面积为a2-b2,图2的面积为
,
∴根据图1和图2的面积相等可得到;
(2)拼图前的面积为,拼图后的面积为,
因此可得;
(3)能拼成长方形.
等式:.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
