七年级数学下册试题 一课一练2.4《用尺规作角》 -北师大版(word版含答案)
文档属性
| 名称 | 七年级数学下册试题 一课一练2.4《用尺规作角》 -北师大版(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 505.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 00:00:00 | ||
图片预览




文档简介
2.4《用尺规作角》
一、解答题
1.如图,线段交于.
(1)尺规作图:以点为顶点,射线为一边,在的右侧作,使.(要求:不写作法,但保留作图痕迹并写出结论)
(2)判断与的位置关系并说明理由;
2.作图题:已知∠α,线段m、n,请按下列步骤完成作图(不需要写作法,保留作图痕迹)
(1)作∠MON=∠α
(2)在边OM上截取OA=m,在边ON上截取OB=n.
(3)作直线AB.
3.如图,已知中,,点在上.
(1)试用直尺和圆规在上找一点,使(不写作法,但需保留作图痕迹);
(2)在(1)的条件下,若;求证:.
4.如图,在线段MN上求作一点P,使∠APM=∠BPM,(保留作图痕迹,不必写出作法与证明).
5.用圆规、直尺作图,不写作法,但要保留作图痕迹.
如图,王师傅开车在一条公路上经过点B和点C处两次拐弯后继续前行,且前行方向和原来的方向AB相同.已知第一次的拐角为∠ABC,请借助圆规和直尺作出第二次拐弯后的拐角∠BCD.
6.如图所示,已知和.
(1)以为一边在的外部画,;
(2)画出的平分线;
(3)量一量,的度数是多少?
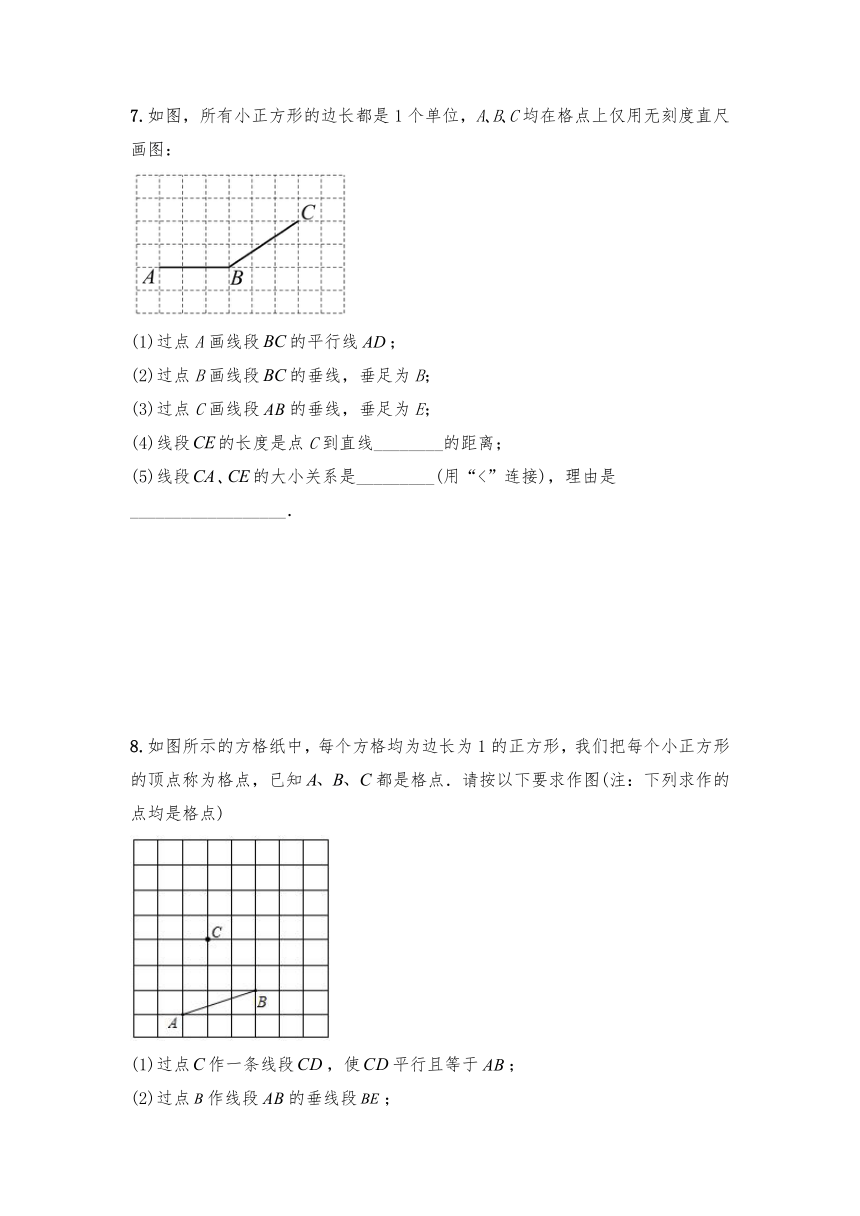
7.如图,所有小正方形的边长都是1个单位,A?B?C均在格点上仅用无刻度直尺画图:
(1)过点A画线段的平行线;
(2)过点B画线段的垂线,垂足为B;
(3)过点C画线段的垂线,垂足为E;
(4)线段的长度是点C到直线________的距离;
(5)线段?的大小关系是_________(用“<”连接),理由是__________________.
8.如图所示的方格纸中,每个方格均为边长为1的正方形,我们把每个小正方形的顶点称为格点,已知都是格点.请按以下要求作图(注:下列求作的点均是格点)
(1)过点作一条线段,使平行且等于;
(2)过点作线段的垂线段;
(3)过点作线段的垂线段,并判断与的位置关系;
(4)求的面积.
9.如图,点P是的边上的一点.
(1)过点P画的垂线,交于点E;
(2)过点P画的垂线,垂足为H;
(3)过点P画的平行线;
(4)若每个小正方形的边长是1,则点P到的距离是___________;
(5)线段的大小关系是_____________________(用“<”连接).
10.利用网格画图,每个小正方形边长均为1
(1)过点C画AB的平行线CD;
(2)仅用直尺,过点C画AB的垂线,垂足为E;
(3)连接CA、CB,在线段CA、CB、CE中,线段______最短,理由___________.
(4)直接写出△ABC的面积为
_________.
11.如图,所有小正方形的边长都是1个单位,A?B?C均在格点上仅用无刻度直尺画图:
(1)过点A画线段的平行线;
(2)过点B画线段的垂线,垂足为B;
(3)过点C画线段的垂线,垂足为E;
(4)线段的长度是点C到直线________的距离;
(5)线段?的大小关系是_________(用“<”连接),理由是__________________.
12.在如图所示的方格纸中,每个小正方形的顶点称为格点,点都在格点上.
找一格点,使得直线,画出直线;
找一格点,使得直线于点,画出直线,并注明垂足;
找一格点,使得直线,画出直线;
连接,则线段的大小关系是
(用“”连接).
13.已知方格纸上点O和线段AB,根据下列要求画图:
(1)画直线OA;
(2)过B点画直线OA的垂线,垂足为D;
(3)取线段AB的中点E,过点E画BD的平行线,交AO于点F.
14.如图,平面上有一条直线AB以及AB外一点P,请你只用一块含30°角的三角板经过P点画直线CD使CD∥AB,简单说明你的画法.
15.如图,都是射线,且.
(1)按要求画图:过画的垂线,垂足为,过画的平行线交于;
(2)在(1)画出的图形中,比较与的大小,并写出理由.
答案
一、解答题
1.解:(1)如图所示,∠EFG即为所求;
(2)
∥.理由,如图,
∵,
∴∠B=∠1,
∵由作图知∠B=∠F,
∴∠1=∠F,
∴∥.
2.解:(1)如图所示,
(2)如图所示,
(3)如图所示,
3.解:(1)如图所示.
(2)∵
∴
∵
∴
∴.
4.解:如图,点P即为所求.
5.
由题意得:,
,
根据作一个角等于已知角的尺规作图法作图如下:
则即为所求作.
6.
(1)(2)如图所示:、射线OD即为所求;
(3)利用量角器量得,.
7.(1)如图,直线即为所求;
(2)如图,直线即为所求
(3)如图,直线即为所求;
(4)
(5);垂线段最短.
8.(1)每个方格均为边长为1的正方形,结合题意,作图如下:
(2)如图,
∵,,
使,,
连接BE,线段即为所求;
(3)如图,连接CQ,直线CQ与AB相交于点F
即为线段的垂线段;
∵,且
∴
(4)如图
∵每个方格均为边长为1的正方形
∴正方形面积-
∴.
9.如图,点P是的边上的一点.
(1)过点P画的垂线,交于点E;
(2)过点P画的垂线,垂足为H;
(3)过点P画的平行线;
(4)由题意PH即点P到的距离,且PH=1,
∴答案为1;
(5)∵在RT△PHE中,PH是直角边,PE是斜边,
∴PH同理在RT△POE中,PE是直角边,OE是斜边,
∴PE∴线段,,的大小关系是.
故答案为PH10.解:
(1)直线CD即为所求;
(2)直线CE即为所求;
(3)在线段CA、CB、CE中,线段CE最短,理由:垂线段最短;
故答案为CE,垂线段最短;
(4)
S△ABC=18﹣×1×5﹣×1×3﹣×2×6=8,
∴△ABC的面积为8.
11.(1)如图,直线即为所求;
(2)如图,直线即为所求
(3)如图,直线即为所求;
(4)
(5);垂线段最短.
12.(1)如图所示,符合题意的格点有D1,D2两个,画出其中一个即可;
(2)如图所示:E点即为所求,垂足为F点;
(3)如图所示,点G即为所求;
(4)如图所示,显然,在中,;在中,,
故答案为:.
13.解:(1)作法:①连接OA,②作直线AO;
(2)作法:连接正方形AHGB的对角线BH交AG于点D;
(3)作法:①取线段AD的中点F,连接EF.
14.解:如下图所示,将三角板30°角的一边与直线AB重合,另一边过点P,沿着这边作直线EF,平移三角板,当30°角的顶点与点P重合时,沿着30°角的另一边画直线CD,根据同位角相等,两直线平行可得CD∥AB,
∴直线CD即为所求.
15.(1)如图所示;
(2)
理由:垂线段最短.
一、解答题
1.如图,线段交于.
(1)尺规作图:以点为顶点,射线为一边,在的右侧作,使.(要求:不写作法,但保留作图痕迹并写出结论)
(2)判断与的位置关系并说明理由;
2.作图题:已知∠α,线段m、n,请按下列步骤完成作图(不需要写作法,保留作图痕迹)
(1)作∠MON=∠α
(2)在边OM上截取OA=m,在边ON上截取OB=n.
(3)作直线AB.
3.如图,已知中,,点在上.
(1)试用直尺和圆规在上找一点,使(不写作法,但需保留作图痕迹);
(2)在(1)的条件下,若;求证:.
4.如图,在线段MN上求作一点P,使∠APM=∠BPM,(保留作图痕迹,不必写出作法与证明).
5.用圆规、直尺作图,不写作法,但要保留作图痕迹.
如图,王师傅开车在一条公路上经过点B和点C处两次拐弯后继续前行,且前行方向和原来的方向AB相同.已知第一次的拐角为∠ABC,请借助圆规和直尺作出第二次拐弯后的拐角∠BCD.
6.如图所示,已知和.
(1)以为一边在的外部画,;
(2)画出的平分线;
(3)量一量,的度数是多少?
7.如图,所有小正方形的边长都是1个单位,A?B?C均在格点上仅用无刻度直尺画图:
(1)过点A画线段的平行线;
(2)过点B画线段的垂线,垂足为B;
(3)过点C画线段的垂线,垂足为E;
(4)线段的长度是点C到直线________的距离;
(5)线段?的大小关系是_________(用“<”连接),理由是__________________.
8.如图所示的方格纸中,每个方格均为边长为1的正方形,我们把每个小正方形的顶点称为格点,已知都是格点.请按以下要求作图(注:下列求作的点均是格点)
(1)过点作一条线段,使平行且等于;
(2)过点作线段的垂线段;
(3)过点作线段的垂线段,并判断与的位置关系;
(4)求的面积.
9.如图,点P是的边上的一点.
(1)过点P画的垂线,交于点E;
(2)过点P画的垂线,垂足为H;
(3)过点P画的平行线;
(4)若每个小正方形的边长是1,则点P到的距离是___________;
(5)线段的大小关系是_____________________(用“<”连接).
10.利用网格画图,每个小正方形边长均为1
(1)过点C画AB的平行线CD;
(2)仅用直尺,过点C画AB的垂线,垂足为E;
(3)连接CA、CB,在线段CA、CB、CE中,线段______最短,理由___________.
(4)直接写出△ABC的面积为
_________.
11.如图,所有小正方形的边长都是1个单位,A?B?C均在格点上仅用无刻度直尺画图:
(1)过点A画线段的平行线;
(2)过点B画线段的垂线,垂足为B;
(3)过点C画线段的垂线,垂足为E;
(4)线段的长度是点C到直线________的距离;
(5)线段?的大小关系是_________(用“<”连接),理由是__________________.
12.在如图所示的方格纸中,每个小正方形的顶点称为格点,点都在格点上.
找一格点,使得直线,画出直线;
找一格点,使得直线于点,画出直线,并注明垂足;
找一格点,使得直线,画出直线;
连接,则线段的大小关系是
(用“”连接).
13.已知方格纸上点O和线段AB,根据下列要求画图:
(1)画直线OA;
(2)过B点画直线OA的垂线,垂足为D;
(3)取线段AB的中点E,过点E画BD的平行线,交AO于点F.
14.如图,平面上有一条直线AB以及AB外一点P,请你只用一块含30°角的三角板经过P点画直线CD使CD∥AB,简单说明你的画法.
15.如图,都是射线,且.
(1)按要求画图:过画的垂线,垂足为,过画的平行线交于;
(2)在(1)画出的图形中,比较与的大小,并写出理由.
答案
一、解答题
1.解:(1)如图所示,∠EFG即为所求;
(2)
∥.理由,如图,
∵,
∴∠B=∠1,
∵由作图知∠B=∠F,
∴∠1=∠F,
∴∥.
2.解:(1)如图所示,
(2)如图所示,
(3)如图所示,
3.解:(1)如图所示.
(2)∵
∴
∵
∴
∴.
4.解:如图,点P即为所求.
5.
由题意得:,
,
根据作一个角等于已知角的尺规作图法作图如下:
则即为所求作.
6.
(1)(2)如图所示:、射线OD即为所求;
(3)利用量角器量得,.
7.(1)如图,直线即为所求;
(2)如图,直线即为所求
(3)如图,直线即为所求;
(4)
(5);垂线段最短.
8.(1)每个方格均为边长为1的正方形,结合题意,作图如下:
(2)如图,
∵,,
使,,
连接BE,线段即为所求;
(3)如图,连接CQ,直线CQ与AB相交于点F
即为线段的垂线段;
∵,且
∴
(4)如图
∵每个方格均为边长为1的正方形
∴正方形面积-
∴.
9.如图,点P是的边上的一点.
(1)过点P画的垂线,交于点E;
(2)过点P画的垂线,垂足为H;
(3)过点P画的平行线;
(4)由题意PH即点P到的距离,且PH=1,
∴答案为1;
(5)∵在RT△PHE中,PH是直角边,PE是斜边,
∴PH
∴PE
故答案为PH
(1)直线CD即为所求;
(2)直线CE即为所求;
(3)在线段CA、CB、CE中,线段CE最短,理由:垂线段最短;
故答案为CE,垂线段最短;
(4)
S△ABC=18﹣×1×5﹣×1×3﹣×2×6=8,
∴△ABC的面积为8.
11.(1)如图,直线即为所求;
(2)如图,直线即为所求
(3)如图,直线即为所求;
(4)
(5);垂线段最短.
12.(1)如图所示,符合题意的格点有D1,D2两个,画出其中一个即可;
(2)如图所示:E点即为所求,垂足为F点;
(3)如图所示,点G即为所求;
(4)如图所示,显然,在中,;在中,,
故答案为:.
13.解:(1)作法:①连接OA,②作直线AO;
(2)作法:连接正方形AHGB的对角线BH交AG于点D;
(3)作法:①取线段AD的中点F,连接EF.
14.解:如下图所示,将三角板30°角的一边与直线AB重合,另一边过点P,沿着这边作直线EF,平移三角板,当30°角的顶点与点P重合时,沿着30°角的另一边画直线CD,根据同位角相等,两直线平行可得CD∥AB,
∴直线CD即为所求.
15.(1)如图所示;
(2)
理由:垂线段最短.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
