人教版六年级数学上册《数与形》课件(28张ppt)
文档属性
| 名称 | 人教版六年级数学上册《数与形》课件(28张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 10:13:57 | ||
图片预览





文档简介
(共28张PPT)
数
与
形
人教版六年级数学上册
1
探究新知
2
运用知识
3
数学练习
4
课后扩展
目
录
1
探究新知
1
1+3
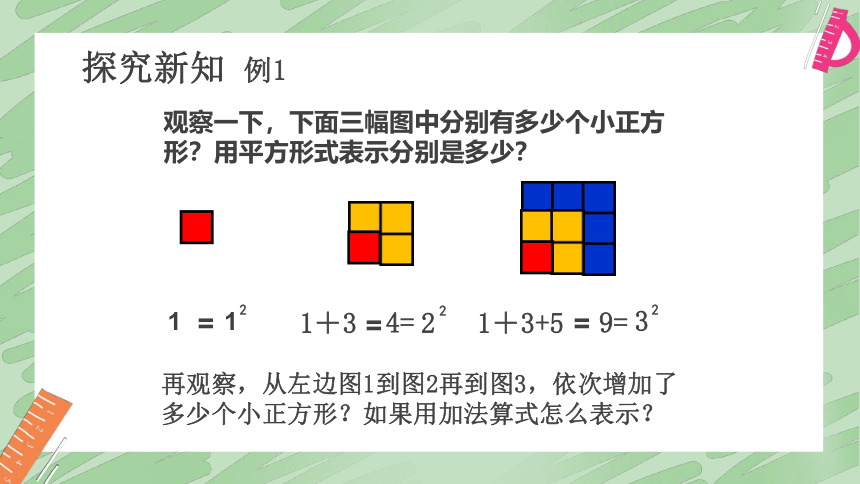
观察一下,下面三幅图中分别有多少个小正方形?用平方形式表示分别是多少?
探究新知
例1
2
1
2
2
2
3
1+3+5
=
=
=
再观察,从左边图1到图2再到图3,依次增加了多少个小正方形?如果用加法算式怎么表示?
4=
9=
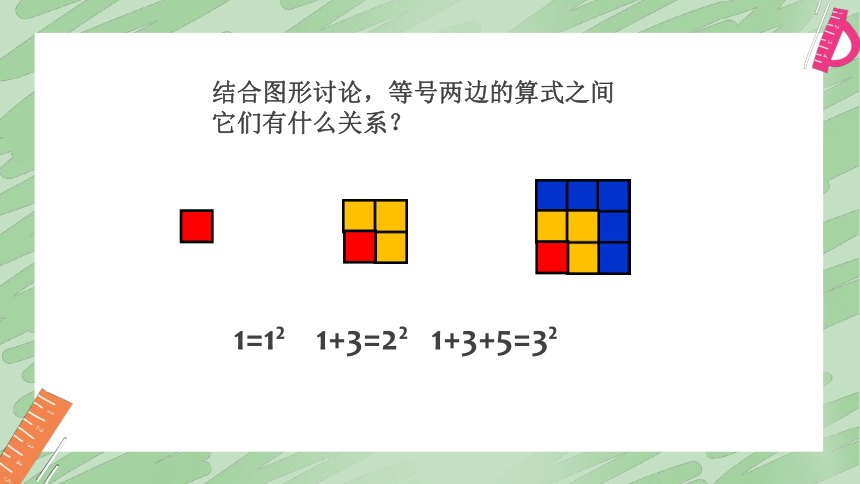
结合图形讨论,等号两边的算式之间它们有什么关系?
1=1?
1+3=2?
1+3+5=3?
如果继续这样摆下去,第4个、第5个大正方形各需要几个小正方形?
1+3+5+
2
1+3+5+7+
2
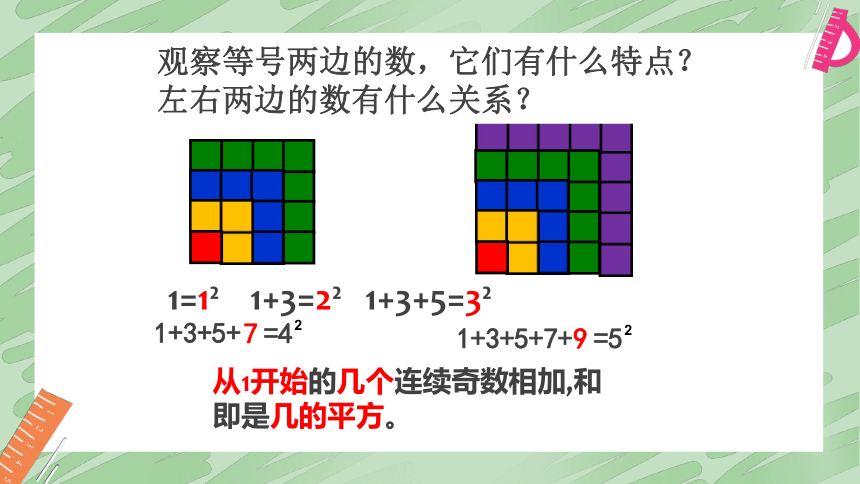
从1开始的几个连续奇数相加,和即是几的平方。
7
=4
9
=5
1=1?
1+3=2?
1+3+5=3?
观察等号两边的数,它们有什么特点?左右两边的数有什么关系?
2
运用知识
1+3+5+7=(
)
1+3+5+7+9+11+13
=(
)
1.
你能利用规律直接写一写吗?
4?
7?
1+3+5+7+9+11+13+15+17
=9?
运用知识
从1开始的n个连续奇数相加,和就是n的平方。
1+3+5+7+9+…=(
)
n个
n
2
1+3+5+7+5+3+1
=(
)
2.
请根据例1的结论算一算。
25
可以看成两部分:1+3+5+7=42
5+3+1=
32
42+
32
=25
运用知识
1+3+5+7+9+11+13+11+9+7+5+3+1=(
)
85
3.
请根据例1的结论算一算。
运用知识
1+3+5+7+5+3+1
=(
25)
6
2
7
2
1+3+7+9+11+13=(
)
可以这么看
1+3+5+7+9+11+13=72
7?-5=44
7?
-5
1+3+7+9+11=
1+3+7+9+11+13
=(
44
)
1+3+5+7+11+13+15+17
=(
)
9?-9
72
3
数学练习
1
1
2
1
1
4
1
8
1
32
+
64
+
+
16
+
+
+
……。
你能发现什么规律?
从第二个数开始,每个数是前一个数的
。
2
1
我一个一个加下去看看,
答案好像有点规律。
1
2
+
1
4
=
3
4
3
4
+
1
8
=
7
8
+
1
16
7
8
=
15
16
1
32
+
=
31
32
15
16
…
加下去,等号右边的分数
越来越接近于1。
计算。
探究新知
二、探究新知
1
1
2
1
1
4
1
8
1
32
+
64
+
+
16
+
+
+
……。
=1
1
2
+
1
4
=
3
4
3
4
+
1
8
=
7
8
+
1
16
7
8
=
15
16
1
32
+
=
15
16
…
31
32
2
1
4
1
16
1
8
1
…
32
1
8
7
4
3
16
15
32
31
64
63
128
127
计算。
1
2
+
=
1
4
3
4
1
2
1
4
3
4
3
4
+
=
1
8
7
8
7
8
1
8
7
8
+
=
16
1
16
15
16
1
32
1
16
15
32
1
16
15
+
=
32
31
32
31
64
63
128
127
1
2
+
1
4
+
1
8
+
16
1
+
32
1
+
64
1
+
……。
=1
…
…
计算。
计算。
二、探究新知
照这样画下去,第4个图形最外圈有(
)个小正方形。
照这样画下去,第5个图形最外圈有(
)个小正方形。
4.
下面每个图中最外圈有多少个小正方形?
40
3
-1=
8
2
5
-3
=
16
2
2
7
-5
=
24
2
2
11
-9
=
40
2
2
运用知识
32
9
-7
=
32
2
2
每个图中最外圈各有多少个小正方形?你能解释这其中的道理吗?
16
8
24
32
40
8n
1
3
6
10
15
21
照这样画下去,第10个图形下面的数字是多少?
拓展延伸
1
2
3
4
5
6
7
8
9
10
1+2+3+4+5+6+7+8+9+10=
(1+10)
×10÷2=55
1
3
6
10
15
21
由于数量为1、3、6、10、15……相同的小图形可以组成一个三角形,这些数也叫做“三角形数”。
16
25
9
4
1
由于数量为1、4、9、16、25……的小正方形可以组成一个大正方形,这些数也叫做“正方形数”。
杨辉三角的特征:它的两条斜边都是由数字1组成的,而其余的数则是等于它肩上的两个数之和
杨辉(宋代)
数形结合百般好,隔裂分家万事休。
——数学家华罗庚
4
课后扩展
拓展延伸
运用例1学到的思考方法,能直接算出下面式子的结果吗?
2+4+6+8+10+12+14+16+18+20=(
)
规律:从2开始的n个连续偶数的和等于
。
从2开始连续的偶数相加的情况如下:
2=2=1×2,
2+4=6=2×3,
2+4+6=12=3×4,
2+4+6+8=20=4×5,
(1)请猜想从2开始n个连续偶数相加的和是多少?
数
与
形
人教版六年级数学上册
1
探究新知
2
运用知识
3
数学练习
4
课后扩展
目
录
1
探究新知
1
1+3
观察一下,下面三幅图中分别有多少个小正方形?用平方形式表示分别是多少?
探究新知
例1
2
1
2
2
2
3
1+3+5
=
=
=
再观察,从左边图1到图2再到图3,依次增加了多少个小正方形?如果用加法算式怎么表示?
4=
9=
结合图形讨论,等号两边的算式之间它们有什么关系?
1=1?
1+3=2?
1+3+5=3?
如果继续这样摆下去,第4个、第5个大正方形各需要几个小正方形?
1+3+5+
2
1+3+5+7+
2
从1开始的几个连续奇数相加,和即是几的平方。
7
=4
9
=5
1=1?
1+3=2?
1+3+5=3?
观察等号两边的数,它们有什么特点?左右两边的数有什么关系?
2
运用知识
1+3+5+7=(
)
1+3+5+7+9+11+13
=(
)
1.
你能利用规律直接写一写吗?
4?
7?
1+3+5+7+9+11+13+15+17
=9?
运用知识
从1开始的n个连续奇数相加,和就是n的平方。
1+3+5+7+9+…=(
)
n个
n
2
1+3+5+7+5+3+1
=(
)
2.
请根据例1的结论算一算。
25
可以看成两部分:1+3+5+7=42
5+3+1=
32
42+
32
=25
运用知识
1+3+5+7+9+11+13+11+9+7+5+3+1=(
)
85
3.
请根据例1的结论算一算。
运用知识
1+3+5+7+5+3+1
=(
25)
6
2
7
2
1+3+7+9+11+13=(
)
可以这么看
1+3+5+7+9+11+13=72
7?-5=44
7?
-5
1+3+7+9+11=
1+3+7+9+11+13
=(
44
)
1+3+5+7+11+13+15+17
=(
)
9?-9
72
3
数学练习
1
1
2
1
1
4
1
8
1
32
+
64
+
+
16
+
+
+
……。
你能发现什么规律?
从第二个数开始,每个数是前一个数的
。
2
1
我一个一个加下去看看,
答案好像有点规律。
1
2
+
1
4
=
3
4
3
4
+
1
8
=
7
8
+
1
16
7
8
=
15
16
1
32
+
=
31
32
15
16
…
加下去,等号右边的分数
越来越接近于1。
计算。
探究新知
二、探究新知
1
1
2
1
1
4
1
8
1
32
+
64
+
+
16
+
+
+
……。
=1
1
2
+
1
4
=
3
4
3
4
+
1
8
=
7
8
+
1
16
7
8
=
15
16
1
32
+
=
15
16
…
31
32
2
1
4
1
16
1
8
1
…
32
1
8
7
4
3
16
15
32
31
64
63
128
127
计算。
1
2
+
=
1
4
3
4
1
2
1
4
3
4
3
4
+
=
1
8
7
8
7
8
1
8
7
8
+
=
16
1
16
15
16
1
32
1
16
15
32
1
16
15
+
=
32
31
32
31
64
63
128
127
1
2
+
1
4
+
1
8
+
16
1
+
32
1
+
64
1
+
……。
=1
…
…
计算。
计算。
二、探究新知
照这样画下去,第4个图形最外圈有(
)个小正方形。
照这样画下去,第5个图形最外圈有(
)个小正方形。
4.
下面每个图中最外圈有多少个小正方形?
40
3
-1=
8
2
5
-3
=
16
2
2
7
-5
=
24
2
2
11
-9
=
40
2
2
运用知识
32
9
-7
=
32
2
2
每个图中最外圈各有多少个小正方形?你能解释这其中的道理吗?
16
8
24
32
40
8n
1
3
6
10
15
21
照这样画下去,第10个图形下面的数字是多少?
拓展延伸
1
2
3
4
5
6
7
8
9
10
1+2+3+4+5+6+7+8+9+10=
(1+10)
×10÷2=55
1
3
6
10
15
21
由于数量为1、3、6、10、15……相同的小图形可以组成一个三角形,这些数也叫做“三角形数”。
16
25
9
4
1
由于数量为1、4、9、16、25……的小正方形可以组成一个大正方形,这些数也叫做“正方形数”。
杨辉三角的特征:它的两条斜边都是由数字1组成的,而其余的数则是等于它肩上的两个数之和
杨辉(宋代)
数形结合百般好,隔裂分家万事休。
——数学家华罗庚
4
课后扩展
拓展延伸
运用例1学到的思考方法,能直接算出下面式子的结果吗?
2+4+6+8+10+12+14+16+18+20=(
)
规律:从2开始的n个连续偶数的和等于
。
从2开始连续的偶数相加的情况如下:
2=2=1×2,
2+4=6=2×3,
2+4+6=12=3×4,
2+4+6+8=20=4×5,
(1)请猜想从2开始n个连续偶数相加的和是多少?
