人教版五年级数学上册课件 位 置(31页ppt)
文档属性
| 名称 | 人教版五年级数学上册课件 位 置(31页ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 11:10:17 | ||
图片预览








文档简介
(共31张PPT)
位
置
人教版部编版五年级数学上册
目
录
导入新课
1
巩固提升
3
新课讲解
2
课堂小结
4
01
导入新课
从前到后
横排叫做行。
导入新课
竖排叫做列
从左到右
导入新课
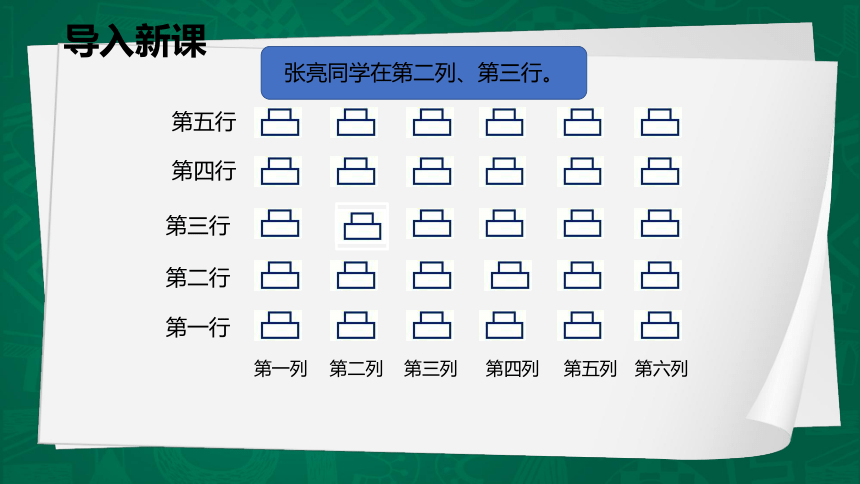
第一行
第二行
第三行
第四行
第五行
第一列
第二列
第三列
第四列
第五列
第六列
张亮同学在第二列、第三行。
导入新课
02
新课讲解
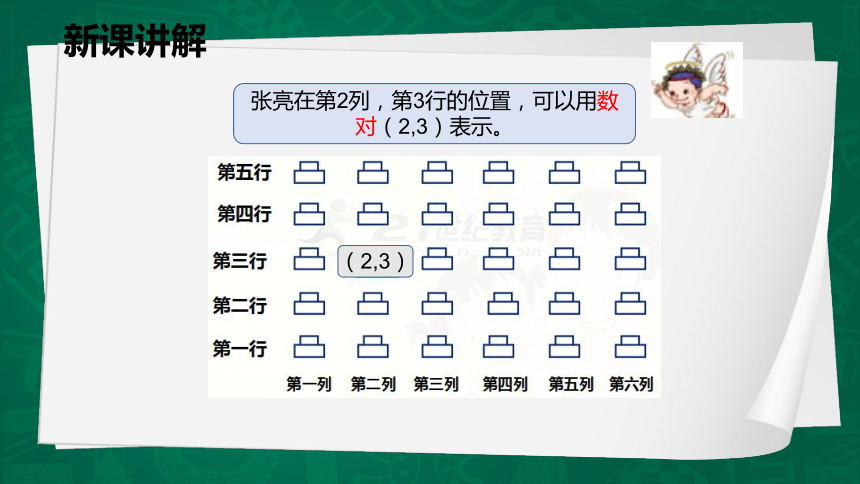
张亮在第2列,第3行的位置,可以用数对(2,3)表示。
(2,3)
新课讲解
什么是数对?
数对:由两个数组成,中间用逗号隔开,用括号括起来。
小组讨论
新课讲解
1、怎样用数对表示物体的位置?2、书写规律是什么?
1、用数对表示物体的位置,要先确定列数,再确定行数。
2、?括号;?列数再前,行数再后;?逗号再中间。
小组讨论
新课讲解
王艳同学的位置用数对表示为(
,
)
赵雪同学的位置用数对表示是(
,
)
看一看他们有什么不同?
3
4
4
3
他们所在的行和列都不同。
新课讲解
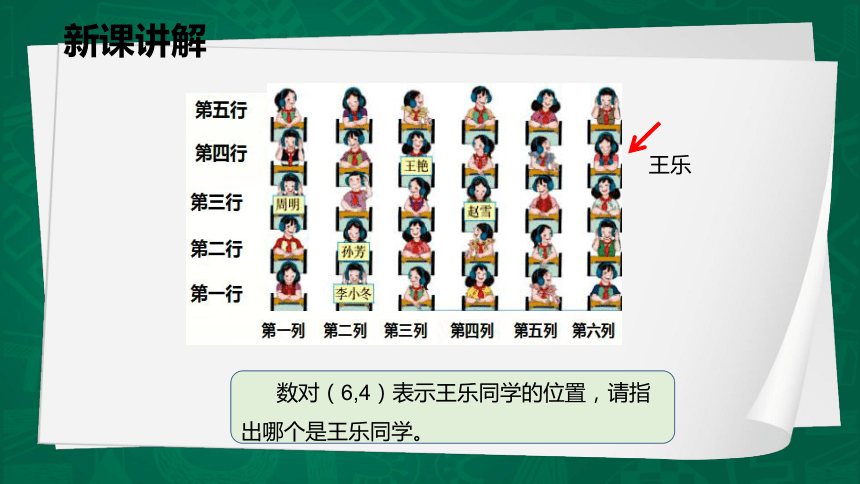
数对(6,4)表示王乐同学的位置,请指出哪个是王乐同学。
王乐
新课讲解
猜猜他是谁?
(2,4)
(4,2)
(1,4)
(4,1)
(3,5)
(5,3)
相同颜色的图片上的数对表示的是一个位置吗?
每组表示的不是同一个位置,行和列都不相同。
新课讲解
请第四列同学起立!
(
4
,
1
)
(
4
,
2
)
(
4
,
3
)
(
4
,
4
)
这些数对有什么特点?
(
1
,
2
)
(
2
,
2
)
(
3
,
2
)
(
4
,
2
)
这些数对表示的位置在哪里?
列数相同,行数不同。
都在第二行。
新课讲解
(
4
,
x
)
请符合要求的同学起立!
(
y
,
3
)
(
y
,
x
)
你为什么要起立?
(
x
,
x
)
我在第四列。
我在第三行。
我在的行、列不同。
我在的行、列相同。
新课讲解
用数对(3,2)表示。你能用数对表示其他几个图案吗?
(2
,
3)
(4
,
3)
(2
,
1)
(4
,
1)
新课讲解
你能用数对表示图中的场馆吗?
大
门
熊猫馆
猴
山
大象馆
海洋馆
(3,0)
(3,5)
(2,2)
(1,4)
(6,4)
新课讲解
在图上标出下列场馆的位置。
飞禽馆(1,1)
猩猩馆(0,3)狮虎山(4,3)
.飞禽馆
.猩猩馆
.狮虎山
观察上面各馆的位置,你有什么发现?
猩猩馆和狮虎山在同一行上,飞禽馆和大象馆在同一列上。
新课讲解
03
巩固提升
怎样在方格纸上用数对确定物体的位置?
在方格纸上用数对确定物体的位置,先找出数对表示的是第几行,第几列,然后在列数与行数相交处描点,表示为(列,行)。
小组讨论
巩固提升
照样子写出字母的位置。
A
B
C
D
(
2
,
5
)
(
5
,
2
)
(
8
,
5
)
(
5
,
8
)
巩固提升
描出下面各点并依次连成封闭图形,看看是什么图形。
A(
5,9
)
B(
2
,
1
)
C(
9
,
6
)
D(
1
,
6
)
E(
8
,
1
)
B
C
D
E
巩固提升
(1)先用数对表示三角形各定点的位置,再分别画出三角形向右平移和向上平移5个格后的图形。
(2)用数对表示所得图形定点的位置,并说说你的发现。
说说你的发现
2
3
2
3
(6,1)
(9,1)
(7,3)
(1,6)
(2,8)
(4,6)
物体向左、右平移,行不变,列数加上或减去平移的格数。
物体向上、下平移,列不变,行数加上或减去平移的格数。
巩固提升
看图完成下面的问题。
(1)用数对表示位置:
超
市(
,
)
学
校(
,
)
图书馆(
,
)。
(2)在图上标出下列地点位置:
游乐场(
5,2
)
地铁站(
3,7)
医
院(10,4)。
3
3
6
5
9
7
.
游乐场
.
地铁站
.
医院
巩固提升
铺地砖
1
2
3
4
5
6
7
8
9
10
11
10
9
8
7
6
5
4
3
2
1
把彩色地砖铺在以下位置:
(9,3)
(3,4)
(7,4)
(5,5)
(9,5)
(7,6)
巩固提升
这几块拼起来会是什么图形
1
2
3
4
5
6
7
8
9
10
11
10
9
8
7
6
5
4
3
2
1
(6,4)
(7,4)
(8,4)
(7,5)
(7,3)
巩固提升
五年级(2)班同学进行队列表演,每组人数相等,小明站在最后一组的最后一个,用数对表示是(8,6),请问他们班有多少人参加了队列表演?
8×6=48(人)
答:他们班有48人参加了队列表演。
巩固提升
围棋棋盘
象
棋
棋
盘
地图
巩固提升
法国著名数学家笛卡尔,有一天他正在反复思考一个问题:怎样才能把“点”和“数”联系起来呢?突然他看见屋角上的一只蜘蛛在上边左右拉丝。于是在蜘蛛的启示下,笛卡尔用一对有顺序的数表示平面上的一个点,并发明了数对。
巩固提升
04
课堂小结
你这节课有什么收获?
在直线上确定一个点只要一个数据,在平面上确定一个点,需要两个数据,就是今天学习的数对。大家想一想,在三位空间确定一个点需要几个数据
呢?
课堂小结
位
置
人教版部编版五年级数学上册
目
录
导入新课
1
巩固提升
3
新课讲解
2
课堂小结
4
01
导入新课
从前到后
横排叫做行。
导入新课
竖排叫做列
从左到右
导入新课
第一行
第二行
第三行
第四行
第五行
第一列
第二列
第三列
第四列
第五列
第六列
张亮同学在第二列、第三行。
导入新课
02
新课讲解
张亮在第2列,第3行的位置,可以用数对(2,3)表示。
(2,3)
新课讲解
什么是数对?
数对:由两个数组成,中间用逗号隔开,用括号括起来。
小组讨论
新课讲解
1、怎样用数对表示物体的位置?2、书写规律是什么?
1、用数对表示物体的位置,要先确定列数,再确定行数。
2、?括号;?列数再前,行数再后;?逗号再中间。
小组讨论
新课讲解
王艳同学的位置用数对表示为(
,
)
赵雪同学的位置用数对表示是(
,
)
看一看他们有什么不同?
3
4
4
3
他们所在的行和列都不同。
新课讲解
数对(6,4)表示王乐同学的位置,请指出哪个是王乐同学。
王乐
新课讲解
猜猜他是谁?
(2,4)
(4,2)
(1,4)
(4,1)
(3,5)
(5,3)
相同颜色的图片上的数对表示的是一个位置吗?
每组表示的不是同一个位置,行和列都不相同。
新课讲解
请第四列同学起立!
(
4
,
1
)
(
4
,
2
)
(
4
,
3
)
(
4
,
4
)
这些数对有什么特点?
(
1
,
2
)
(
2
,
2
)
(
3
,
2
)
(
4
,
2
)
这些数对表示的位置在哪里?
列数相同,行数不同。
都在第二行。
新课讲解
(
4
,
x
)
请符合要求的同学起立!
(
y
,
3
)
(
y
,
x
)
你为什么要起立?
(
x
,
x
)
我在第四列。
我在第三行。
我在的行、列不同。
我在的行、列相同。
新课讲解
用数对(3,2)表示。你能用数对表示其他几个图案吗?
(2
,
3)
(4
,
3)
(2
,
1)
(4
,
1)
新课讲解
你能用数对表示图中的场馆吗?
大
门
熊猫馆
猴
山
大象馆
海洋馆
(3,0)
(3,5)
(2,2)
(1,4)
(6,4)
新课讲解
在图上标出下列场馆的位置。
飞禽馆(1,1)
猩猩馆(0,3)狮虎山(4,3)
.飞禽馆
.猩猩馆
.狮虎山
观察上面各馆的位置,你有什么发现?
猩猩馆和狮虎山在同一行上,飞禽馆和大象馆在同一列上。
新课讲解
03
巩固提升
怎样在方格纸上用数对确定物体的位置?
在方格纸上用数对确定物体的位置,先找出数对表示的是第几行,第几列,然后在列数与行数相交处描点,表示为(列,行)。
小组讨论
巩固提升
照样子写出字母的位置。
A
B
C
D
(
2
,
5
)
(
5
,
2
)
(
8
,
5
)
(
5
,
8
)
巩固提升
描出下面各点并依次连成封闭图形,看看是什么图形。
A(
5,9
)
B(
2
,
1
)
C(
9
,
6
)
D(
1
,
6
)
E(
8
,
1
)
B
C
D
E
巩固提升
(1)先用数对表示三角形各定点的位置,再分别画出三角形向右平移和向上平移5个格后的图形。
(2)用数对表示所得图形定点的位置,并说说你的发现。
说说你的发现
2
3
2
3
(6,1)
(9,1)
(7,3)
(1,6)
(2,8)
(4,6)
物体向左、右平移,行不变,列数加上或减去平移的格数。
物体向上、下平移,列不变,行数加上或减去平移的格数。
巩固提升
看图完成下面的问题。
(1)用数对表示位置:
超
市(
,
)
学
校(
,
)
图书馆(
,
)。
(2)在图上标出下列地点位置:
游乐场(
5,2
)
地铁站(
3,7)
医
院(10,4)。
3
3
6
5
9
7
.
游乐场
.
地铁站
.
医院
巩固提升
铺地砖
1
2
3
4
5
6
7
8
9
10
11
10
9
8
7
6
5
4
3
2
1
把彩色地砖铺在以下位置:
(9,3)
(3,4)
(7,4)
(5,5)
(9,5)
(7,6)
巩固提升
这几块拼起来会是什么图形
1
2
3
4
5
6
7
8
9
10
11
10
9
8
7
6
5
4
3
2
1
(6,4)
(7,4)
(8,4)
(7,5)
(7,3)
巩固提升
五年级(2)班同学进行队列表演,每组人数相等,小明站在最后一组的最后一个,用数对表示是(8,6),请问他们班有多少人参加了队列表演?
8×6=48(人)
答:他们班有48人参加了队列表演。
巩固提升
围棋棋盘
象
棋
棋
盘
地图
巩固提升
法国著名数学家笛卡尔,有一天他正在反复思考一个问题:怎样才能把“点”和“数”联系起来呢?突然他看见屋角上的一只蜘蛛在上边左右拉丝。于是在蜘蛛的启示下,笛卡尔用一对有顺序的数表示平面上的一个点,并发明了数对。
巩固提升
04
课堂小结
你这节课有什么收获?
在直线上确定一个点只要一个数据,在平面上确定一个点,需要两个数据,就是今天学习的数对。大家想一想,在三位空间确定一个点需要几个数据
呢?
课堂小结
