小学数学人教版五年级上册教学课件《不规则图形的面积》(共16张PPT)
文档属性
| 名称 | 小学数学人教版五年级上册教学课件《不规则图形的面积》(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 461.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 16:10:47 | ||
图片预览




文档简介
(共16张PPT)
不规则图形的面积
人教版五年级上册第六单元
授课教师:稻壳儿
班级:五年级二班
教学目录
1.探索新知
2.当堂检测
4.课后作业
3.课堂总结
复习导入
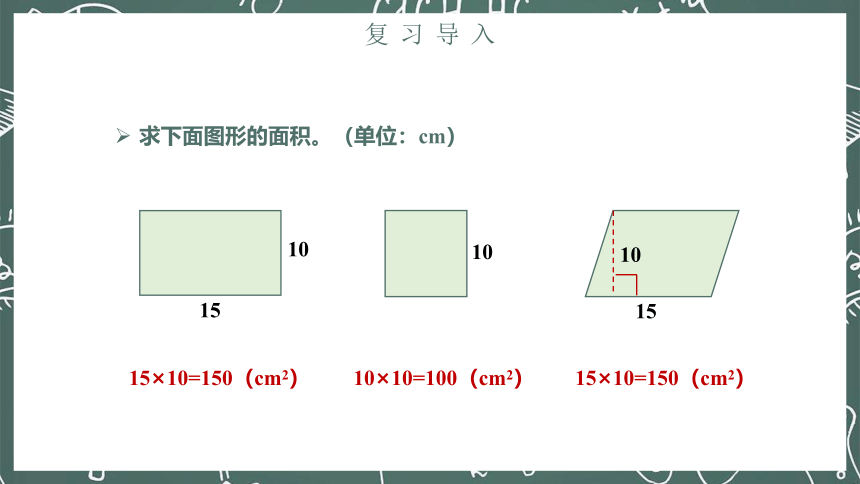
求下面图形的面积。(单位:cm)
10
15
10
15
10
15×10=150(cm2)
10×10=100(cm2)
15×10=150(cm2)
复习导入
求下面图形的面积。(单位:cm)
10
15
10
15
10
15×10÷2=75(cm2)
(10+15)×10÷2=125(cm2)
复习导入
我们已经会计算组合图形的面积了,那么生活中遇到不规则图形我们如何来估算它的面积呢?
这个图形的面积,大家知道该怎么估算么?
探索新知
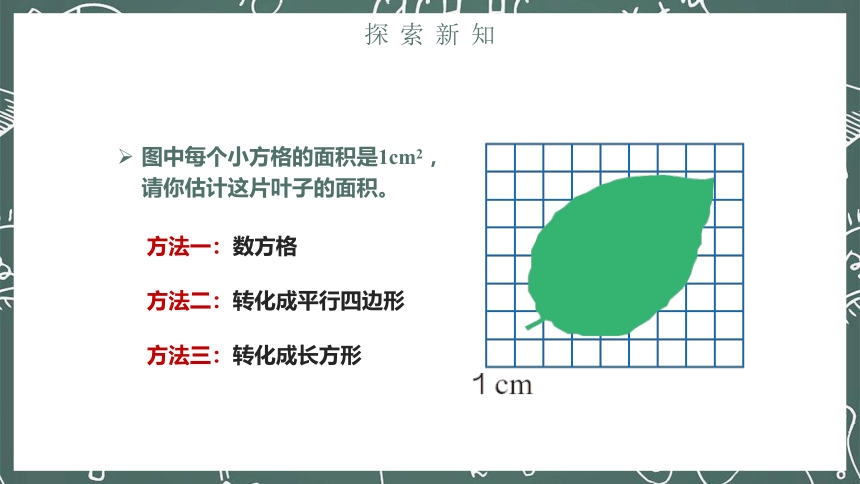
图中每个小方格的面积是1cm2
,请你估计这片叶子的面积。
方法一:数方格
方法二:转化成平行四边形
方法三:转化成长方形
探索新知
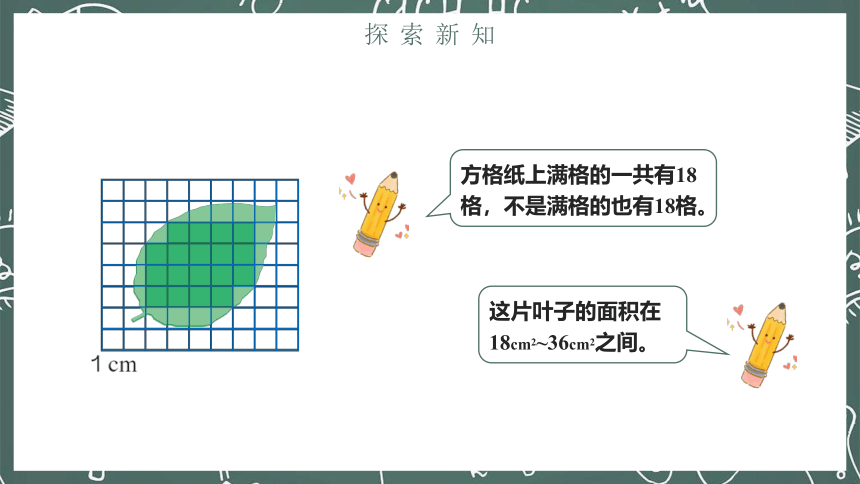
方格纸上满格的一共有18格,不是满格的也有18格。
这片叶子的面积在18cm2~36cm2之间。
探索新知
如果把不满一格的都按半格计算,这片叶子的面积大约是27cm2。
探索新知
用转化的方法,将叶子的图形近似转化成平行四边形,求出平行四边形的面积。
S
=
ah
=
5×6
=
30(cm2
)
因此,叶子的面积大约是30cm2。
探索新知
通过刚才的学习,今后我们再遇到不规则的图形,我们可以怎样估计它的面积呢?
先通过数方格确定图形面积的范围,再估算图形的面积。
不规则的图形可以转化为学过的图形进行估算。
当堂检测
图中每个小方格的面积为1m2
,计算阴影部分面积。
当堂检测
三角形
+
梯形
5×4÷2
+
(5+2)×4÷2
=
10
+
14
=
24(m2)
当堂检测
近似转化成长方形
8×4
=
32(
m2
)
阴影部分面积大约是
32
m2
。
当堂检测
有一块地近似平行四边形,底是43
m,高是20.1
m。这块地的面积约是多少平方米?(得数保留整数。)
43×20.1=864.3(m2)
≈864(m2)
答:这块地的面积约是864m2。
当堂检测
图中每个小方格的面积是1
cm2,计算阴影部分的面积。
(1)7×2÷2+(2+7)×6÷2=34(cm2)
(2)将该图形近似转化成梯形:
则S≈(4+7)×8÷2=44(cm2)
课后作业
请完成教材第101页练习二十二第1题、第2题、第3题、第6题、第7题、第10题。
请完成《学习资料》中习题,具体内容见习题册。
不规则图形的面积
人教版五年级上册第六单元
授课教师:稻壳儿
班级:五年级二班
教学目录
1.探索新知
2.当堂检测
4.课后作业
3.课堂总结
复习导入
求下面图形的面积。(单位:cm)
10
15
10
15
10
15×10=150(cm2)
10×10=100(cm2)
15×10=150(cm2)
复习导入
求下面图形的面积。(单位:cm)
10
15
10
15
10
15×10÷2=75(cm2)
(10+15)×10÷2=125(cm2)
复习导入
我们已经会计算组合图形的面积了,那么生活中遇到不规则图形我们如何来估算它的面积呢?
这个图形的面积,大家知道该怎么估算么?
探索新知
图中每个小方格的面积是1cm2
,请你估计这片叶子的面积。
方法一:数方格
方法二:转化成平行四边形
方法三:转化成长方形
探索新知
方格纸上满格的一共有18格,不是满格的也有18格。
这片叶子的面积在18cm2~36cm2之间。
探索新知
如果把不满一格的都按半格计算,这片叶子的面积大约是27cm2。
探索新知
用转化的方法,将叶子的图形近似转化成平行四边形,求出平行四边形的面积。
S
=
ah
=
5×6
=
30(cm2
)
因此,叶子的面积大约是30cm2。
探索新知
通过刚才的学习,今后我们再遇到不规则的图形,我们可以怎样估计它的面积呢?
先通过数方格确定图形面积的范围,再估算图形的面积。
不规则的图形可以转化为学过的图形进行估算。
当堂检测
图中每个小方格的面积为1m2
,计算阴影部分面积。
当堂检测
三角形
+
梯形
5×4÷2
+
(5+2)×4÷2
=
10
+
14
=
24(m2)
当堂检测
近似转化成长方形
8×4
=
32(
m2
)
阴影部分面积大约是
32
m2
。
当堂检测
有一块地近似平行四边形,底是43
m,高是20.1
m。这块地的面积约是多少平方米?(得数保留整数。)
43×20.1=864.3(m2)
≈864(m2)
答:这块地的面积约是864m2。
当堂检测
图中每个小方格的面积是1
cm2,计算阴影部分的面积。
(1)7×2÷2+(2+7)×6÷2=34(cm2)
(2)将该图形近似转化成梯形:
则S≈(4+7)×8÷2=44(cm2)
课后作业
请完成教材第101页练习二十二第1题、第2题、第3题、第6题、第7题、第10题。
请完成《学习资料》中习题,具体内容见习题册。
