2021-2022学年人教版六年级数学上册分数除法课件(50张PPT)
文档属性
| 名称 | 2021-2022学年人教版六年级数学上册分数除法课件(50张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 16:06:38 | ||
图片预览








文档简介
(共50张PPT)
分数除法
例1
分数除以整数
例2
一个数除以分数
例3
分数混合运算
一、复习导入
说出下面各数的倒数。
4
5
1
7
3
5
11
1
4
1
5
11
5
1
3
7
二、教学例1
分数除以整数
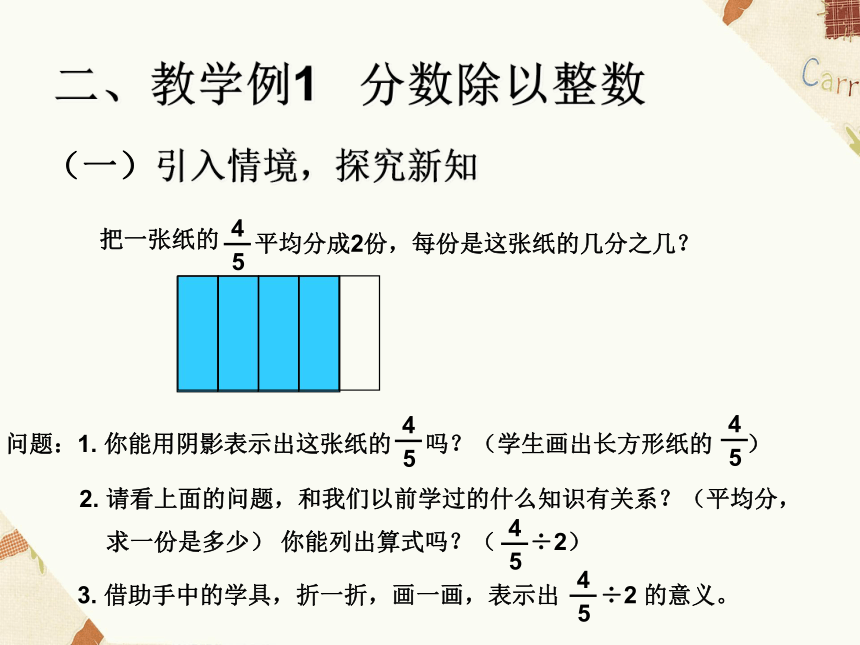
把一张纸的
平均分成2份,每份是这张纸的几分之几?
5
4
2.
请看上面的问题,和我们以前学过的什么知识有关系?(平均分,
求一份是多少)
你能列出算式吗?(
÷2)
5
4
问题:1.
你能用阴影表示出这张纸的
吗?(学生画出长方形纸的
)
5
4
5
4
3.
借助手中的学具,折一折,画一画,表示出
÷2
的意义。
5
4
(一)引入情境,探究新知
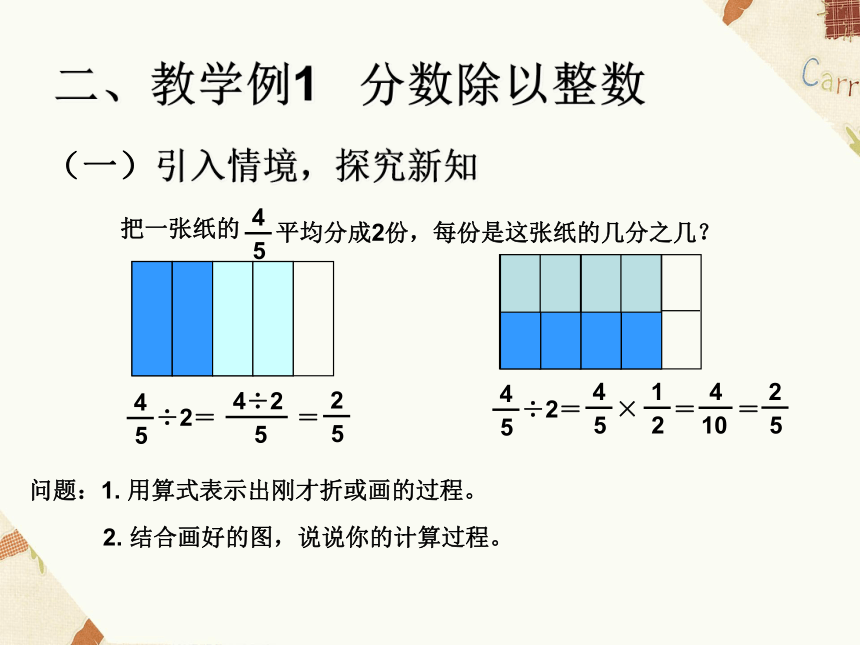
问题:1.
用算式表示出刚才折或画的过程。
2.
结合画好的图,说说你的计算过程。
把一张纸的
平均分成2份,每份是这张纸的几分之几?
5
4
5
4
÷2=
=
5
4÷2
5
2
5
4
÷2=
×
=
=
5
2
5
4
2
1
10
4
二、教学例1
分数除以整数
(一)引入情境,探究新知
(二)自主操作,深入理解
2.
用算式表示出刚才折或画的过程。
4.
比较两种解法,你有什么想法?
3.
结合画好的图,说说你的计算过程。
(出示预设1时)你遇到了什么问题?
5.
根据上面的折纸实验和算式,你能发现什么规律?
(出示预设2)说说你的想法。
把一张纸的
平均分成3份,每份是这张纸的几分之几?
5
4
预设1:
5
4
÷3=
=?
5
4÷3
预设2:
5
4
÷3=
×
=
5
4
3
1
15
4
问题:1.
借助手中的学具,折一折,画一画,表示出
÷3
的意义。
5
4
二、教学例1
分数除以整数
计算下面各题。
(三)巩固练习
10
9
÷3=
×
=
(
)
(
)
(
)
(
)
(
)
(
)
9
10
1
3
3
10
8
3
÷2=
×
=
(
)
(
)
(
)
(
)
(
)
(
)
3
8
1
2
3
16
二、教学例1
分数除以整数
(一)引入情境,探究新知
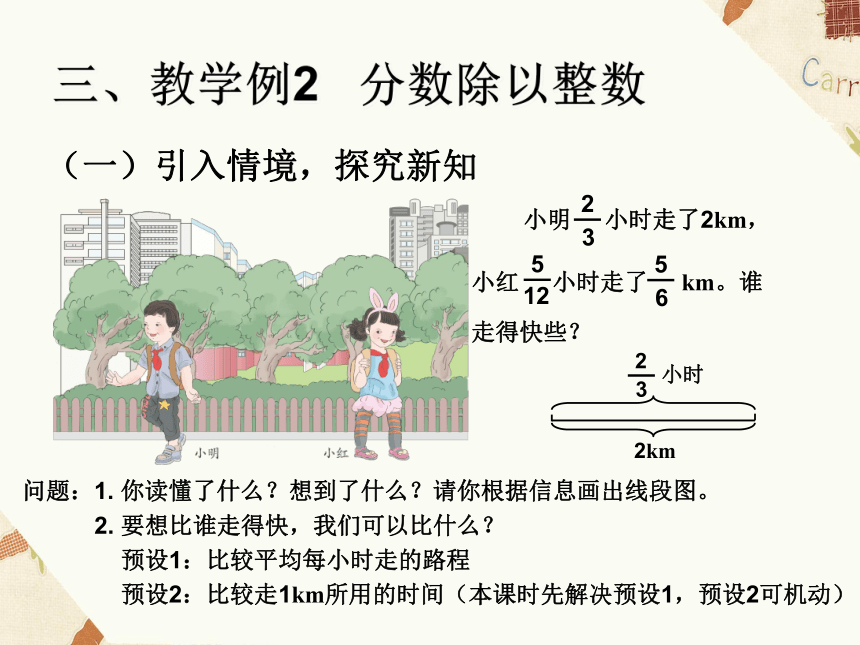
问题:1.
你读懂了什么?想到了什么?请你根据信息画出线段图。
2.
要想比谁走得快,我们可以比什么?
预设1:比较平均每小时走的路程
预设2:比较走1km所用的时间(本课时先解决预设1,预设2可机动)
小明
小时走了2km,
3
2
小红
小时走了
km。谁
走得快些?
12
5
6
5
2km
3
2
小时
三、教学例2
分数除以整数
(二)自主操作,深入理解
解决预设1:小明平均每小时走多少km?
2.
思考,在刚才的线段图上如何表示小明1小时走的路程?
2km
3
2
小时
问题:1.
怎样求上面的问题?用到了我们以前学过的什么知识?
(路程÷时间=速度)请你列出算式。(
)
2÷
3
2
三、教学例2
分数除以整数
小明平均每小时走多少km?
问题:1.
为什么要把2km平均分成2份?
2.
你是怎么想到要补充1份的?
3.
这部分表示什么?
4.
你能用算式表示出所画的意思吗?
5.
结合线段图,说说你是怎么计算的。
2km
3
2
小时
走多少km?
1小时
3
2
2÷
=2
×
×3=2×
=3
(km)
2
3
2
1
1
1
三、教学例2
分数除以整数
(二)自主操作,深入理解
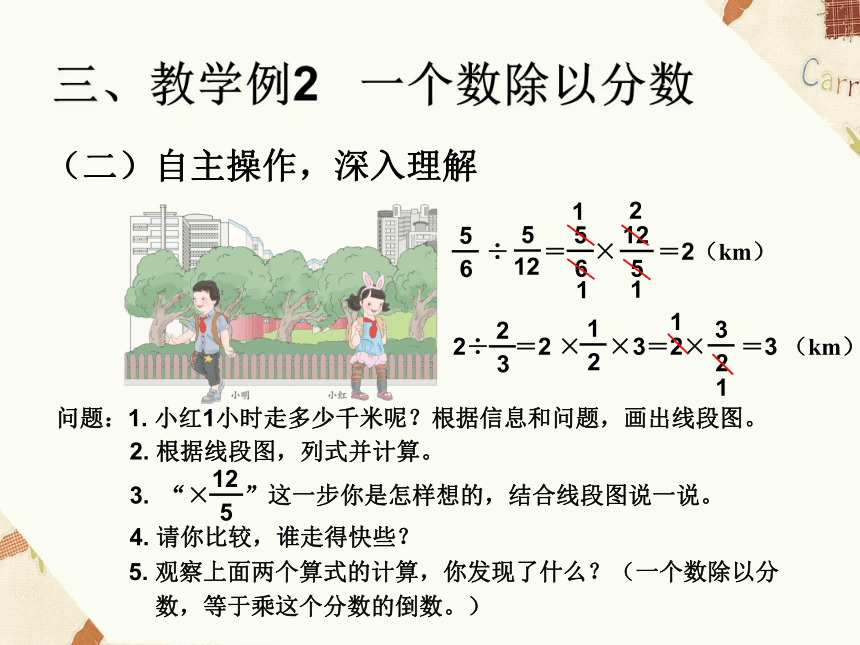
问题:1.
小红1小时走多少千米呢?根据信息和问题,画出线段图。
2.
根据线段图,列式并计算。
4.
请你比较,谁走得快些?
5.
观察上面两个算式的计算,你发现了什么?(一个数除以分
数,等于乘这个分数的倒数。)
3
2
2÷
=2
×
×3=2×
=3
(km)
2
3
2
1
1
1
÷
=
×
=2(km)
12
5
6
5
6
5
5
12
1
2
1
1
3.
“×
”这一步你是怎样想的,结合线段图说一说。
5
12
三、教学例2
一个数除以分数
(二)自主操作,深入理解
(三)巩固练习
1.
计算下面各题
9
8
24÷
=24
(
)
(
)
=(
)
×
9
8
27
5
4
÷
=
16
7
(
)
(
)
(
)
(
)
(
)
(
)
=
7
16
5
4
×
35
64
三、教学例2
一个数除以分数
(一)理解情境,解决问题
四、教学例3
分数乘除混合运算
3.
(出示方法一)谁读懂了它的意思?说一说。
4.
(出示方法二)谁读懂了它的意思?说一说。
问题:1.
你知道了什么?
2.
你能解决这个问题吗?用算式表达你的思考过程。
5.
上面的两种方法,请你用综合算式表示,并写出计算过程。
方法1:
×3
2
1
=
(片)
2
3
12÷
=12×
=8(天)
2
3
3
2
方法2:
12÷
=12×
=24(次)
2
1
1
2
24÷3=8(天)
3.
谁读懂了它的意思,说一说。
问题:1.
你知道了什么?
2.
你能解决这个问题吗?用算式表达你的思考过程。
(二)巩固练习
王叔叔家阁楼上的窗玻璃是梯形的,上底、
下底和高分别是
m、
m、
m。这块玻璃的
面积是多少?
5
3
5
4
4
3
5
3
(
+
)×
÷2
5
4
4
3
=
×
×
5
7
4
3
2
1
=
(
)
40
21
四、教学例3
分数乘除混合运算
五、布置作业
作业:第35页练习七,第7题、第8题。
分数除法
例4
已知一个数的几分之几
是多少求这个数
一、复习导入
阅读下面的句子,说说你的理解。
1.
男生人数占全班人数的
。
5
2
问题:1.
你知道了什么?(男生人数与全班人数比较:全班人数是
单位“1”,男生人数占全班人数的
。)
5
2
5
2
男生
“1”
2.
你还能想到什么?(女生人数占全班人数的
,男生人数
是女生人数的
,女生人数是男生人数的
,……)
5
3
3
2
2
3
二、引入情境,探究新知
(一)收集信息,明确条件问题
小明重多少千克?
问题:你知道了什么?(小明体内的水分重28kg,小明体内的水分占体重
的
,要求的是小明的体重。)
5
4
二、引入情境,探究新知
(二)画图分析,理解数量关系
根据题目的意思,画出线段图。
3.
成人的信息与问题有关系吗?
5
4
水分占体重的
水分28kg
体重?kg
问题:1.
看图,说明图意。(小明身体中水分的重量与体重做比较:小明的体
重是单位“1”,小明体内的水分占体重的
,求小明的体重是多少kg)
5
4
2.
你能列出一个等量关系吗?(小明的体重×
=小明体内水分的质量)
5
4
二、引入情境,探究新知
问题:1.
谁能结合线段图说说对这种解法的理解?
(三)读懂过程,感悟不同方法
2.
你还有其他的解法吗?
预设1:
预设2:
预设3:
解:设小明的体重是x
kg。
x=28
5
4
x=28÷
5
4
x=28×
4
5
x=35
=28÷
5
4
=28×
4
5
=35(kg)
28÷4×5
=7×5
=35(kg)
二、引入情境,探究新知
(四)回顾反思,沟通不同方法
2.
这些不同的算法中有什么相同点与不同点?(单位“1”
相同,数量之间的关系相同。)
解:设小明的体重是x
kg。
x=28
5
4
x=28÷
5
4
x=28×
4
5
x=35
=28÷
5
4
=28×
4
5
=35(kg)
28÷4×5
=7×5
=35(kg)
问题:1.
怎样检验结果是否正确?(35×
=28(kg))
5
4
1.
一杯约250mL的鲜牛奶大约含有
g的钙质,占一个成年人一天
所需钙质的
。一个成年人一天大约需要多少钙质?
4.
你还有别的方法吗?交流与反馈。
问题:1.
你知道了什么?
2.
根据题意画出线段图。
三、巩固练习,提升认识
3.
写出等量关系,列方程解决问题。
10
3
8
3
10
3
预设1:
解:设成年人一天大约需要x
g钙质。
5
4
x=
8
3
x=
÷
8
3
x=
×
x=
10
3
3
8
10
3
预设2:
5
4
÷
8
3
=
×
=
(g)
10
3
3
8
10
3
三、巩固练习,提升认识
16千米/时
2.自行车的速度是摩托车的
,摩托车每小时行多少千米?
5
2
预设1:
解:设摩托车每小时行x千米。
x=16
5
2
x=16÷
5
2
x=16×
x=40
2
5
预设2:
16÷
5
2
=16×
=40(千米)
2
5
问题:1.
你知道了什么?根据题意画出线段图。
2.
你画的线段图和前两道题有什么不同?
4.
谁读懂了它的意思,说一说。还有不同的想法吗?
3.
你能解决这个问题吗?写出你的思考过程。
三、巩固练习,提升认识
3.
(1)图书馆共有多少本书?
(2)图书馆有多少本故事书?
问题:1.
你知道了什么?
2.
解决“图书馆共有多少本书”需要哪个条件?
“图书馆有多少本故事书”呢?
三、巩固练习,提升认识
4.
解决类似的问题,我们要注意什么?(找准和问题对应的条件)
3.
你会解决这两个问题吗?
问题:
(1)图书馆共有多少本书?
(2)图书馆有多少本故事书?
(1)解:设图书馆共有x
本书。
x=320
5
2
x=320÷
5
2
x=320×
x=800
2
5
(2)解:设图书馆共有故事书x
本。
x=320
3
4
x=320÷
3
4
x=320×
x=240
4
3
3.
四、布置作业
作业:第39页练习八,第3题。
分数除法
例5
已知比一个数多(少)
几分之几是多少求这个数
一、复习导入,揭示课题
看图回答问题
问题:
①从图中你知道了什么?
女生人数
男生人数
4
1
多
“1”
②怎样理解“男生人数比女生人数多
”?
(男生人数与女生人数比较;女生人数是单位“1”;把女生人数
平均分成4份,男生人数是(4+1)份。)
4
1
③你能说说男、女生人数之间有怎样的等量关系?
(女生人数×(1+
)=男生人数。)
4
1
二、引入情境,探究新知
(一)阅读与理解
问题:
①从题目中你知道了什么?
③这道题怎样解答,请你根据题意先画出线段图,再找出爸爸
体重和小明体重之间的等量关系,最后列方程解答。
小明的体重是35kg,他的体重比爸爸的体重轻
,
小明爸爸的体重是多少千克?
15
8
②怎样理解“小明的体重比爸爸的体重轻
”?
(小明体重和爸爸体重在比较;爸爸的体重是“1”;把爸爸
体重平均分成15份,小明的体重就是(15-8)份;小明的
体重是爸爸体重的(1-
)。)
15
8
15
8
二、引入情境,探究新知
(二)分析与解答
爸爸的体重-小明比爸爸轻的部分=小明的体重
小明:
预设1:
爸爸:
“1”
小明的体重比爸爸轻
?千克
是爸爸体重的几分之几?
35千克
问题:
①你们能借助线段图理解这个等量关系式和方程的意思吗?
②图中哪部分是小明体重比爸爸轻的部分?
③他是怎样求小明体重比爸爸轻的部分的?
解:设爸爸的体重为x
kg。
x-
x=35
x=35
x=35×
x=75
15
8
15
7
7
15
二、引入情境,探究新知
(二)分析与解答
预设2:
小明的体重比爸爸轻
?千克
35千克
爸爸:
小明:
“1”
是爸爸体重的几分之几?
问题:
①你们能借助线段图理解这个数量关系式和方程的意思吗?
②图中小明的体重相当于爸爸体重的哪一部分?
③小明的体重相当于爸爸体重的几分之几?你是怎样得到的?
爸爸的体重×(1-
)=小明的体重
15
8
解:设爸爸的体重为x
kg。
(1-
)x=35
x=35
x=35×
x=75
15
8
15
7
7
15
二、引入情境,探究新知
(二)分析与解答
小结:
虽然两种解法不同,但是都是依据分数乘法的意义找到等量关系,用方程解答。
爸爸的体重-小明比爸爸轻的部分
=小明的体重
解:设爸爸的体重为x
kg。
x-
x=35
x=35
x=35×
x=75
15
8
15
7
7
15
爸爸的体重×(1-
)=小明的体重
15
8
解:设爸爸的体重为x
kg。
(1-
)x=35
x=35
x=35×
x=75
15
7
7
15
15
8
二、引入情境,探究新知
(三)回顾与反思
问题:
刚才同学们用两种不同的方法求出了爸爸的体重,那么对不对呢?都可以怎样检查?
15
7
预设1:
看看小明的体重是不是爸爸的
35
÷75
=
15
7
预设2:
看看小明的体重是不是比爸爸轻
(75-35
)÷75
=
15
8
15
8
看看小明的体重是不是35千克
预设3:
75
×(1-
)=35
15
8
三、巩固练习,提升认识
“1”
还剩
读了35页
?页
1.
这本课外读物一共有多少页?
这本课外读物我读了35页,还剩下
没读。
7
2
预设1:
解:设这本课外读物一共有x页。
x-
x=35
x=35
x=49
7
2
7
5
预设2:
解:设这本课外读物一共有x页。
(1-
)x=35
x=35
x=49
7
2
7
5
三、巩固练习,提升认识
30人
?人
“1”
篮球队人数:
足球队人数:
多
2.
学校足球队一共有30人,比篮球队的人数多
,篮球队有多少人?
5
1
解:设篮球队有x人。
x+
x=30
x=30
x=25
预设1:
5
1
5
6
预设2:
解:设篮球队有x人。
(1
+
)x=30
x=30
x=25
5
1
5
6
四、布置作业
作业:第47页练习十,第4题。
分数除法
例6
两个未知数的和倍问题
一、复习导入,揭示课题
看图回答问题
问题:
①从图中你知道了什么?
女生人数
男生人数
②根据线段图,你能说说男、女生人数间的数量关系吗?
(男生人数与女生人数比较;女生人数是单位“1”;把女生人数平
均分成4份,男生人数是5份;男生人数是女生人数的
。
女生人数与男生人数比较;男生人数是单位“1”;把男生人数平均
分成5份,女生人数是4份;女生人数是男生人数的
。)
4
5
5
4
③如果男生有x人,女生有多少人?你是怎样得到的?(女生
x人。)
如果女生有x人,男生有多少人?你是怎样得到的?(男生
x人。)
5
4
4
5
二、引入情境,探究新知
(一)阅读与理解
问题:
①从题目中你知道了什么?
③这道题怎样解答,请你根据题意画出线段图。
上半场和下半场各得多少分?
②怎样理解“下半场得分只有上半场的一半”这句话?
(下半场得分和上半场得分在比较;上半场得分看作单位“1”;
下半场得分是上半场的
。)
2
1
二、引入情境,探究新知
(二)分析与解答
问题:
①你们能借助线段图找出一个等量关系式吗?
②上半场和下半场的得分我们都不知道,那怎样设未知数?
(上半场得分+下半场得分=42分)
③请你依据等量关系列方程并解答。
上半场得分:
下半场得分:
“1”
?分
?分
2
1
42分
预设1:
解:设上半场得了x分,则下半场
得了
x分。
x+
x=42
x=42
x=42×
x=28
28×
=14(分)
2
1
2
1
2
3
3
2
2
1
二、引入情境,探究新知
(二)分析与解答
解:设下半场得了x分,则上半场
得了2x分。
x+2x=42
3x=42
x=42
÷3
x=14
42-14=28(分)
问题:
①如果设下半场得了x分,那么我们把谁看作是单位“1”?
②如果把下半场得分看作单位“1”,那么上半场得分是下半场的几倍?
③应该怎样设未知数?说说你列的方程。
(上半场得分+下半场得分=42分)
预设2:
“1”
上半场得分:
下半场得分:
42分
?分
?分
2倍
二、引入情境,探究新知
问题:
我们依据题意画出了相同的线段图,找到了相同的等量关系,为什么同学们列出的方程不一样呢?
(上半场得分+下半场得分=42分)
(上半场得分+下半场得分=42分)
解:设上半场得了x分,则下半场
得了
x分。
x+
x=42
x=42
x=42×
x=28
28×
=14(分)
2
1
2
1
2
3
3
2
2
1
解:设下半场得了x分,则上半场
得了2x分。
x+2x=42
3x=42
x=42
÷3
x=14
42-14=28(分)
(二)分析与解答
二、引入情境,探究新知
(三)回顾与反思
问题:
刚才同学们列出了两个不同的方程,分别求出了上、下半场的得分,那么对不对呢?可以怎样检验?
预设1:
看看上、下半场的得分和是不是42分
28
+14
=42(分)
预设2:
看看下半场得分是不是上半场的
14÷28
=
2
1
2
1
三、巩固练习,提升认识
108万台
“1”
下半年产量:
上半年产量:
?万台
?万台
上半年产量+下半年产量=全年产量
预设1:
1.
某电视厂去年全年生产电视机108万台,其中上
半年产量是下半年的
。这个电视机厂去年上
半年和下半年的产量分别是多少万台?
5
4
解:设下半年生产x万台,则上
半年生产
x万台。
x+
x=108
x=108
x=60
60
×
=48(万台)
5
4
5
4
5
9
5
4
三、巩固练习,提升认识
如果把上半年的产量看作是单位“1”那么下半年的产量是上半年的几分之几?应该怎样设未知数?
问题:
上半年产量+下半年产量=全年产量
预设2:
108万台
“1”
下半年产量:
上半年产量:
?万台
?万台
1.
某电视厂去年全年生产电视机108万台,其中上
半年产量是下半年的
。这个电视机厂去年上
半年和下半年的产量分别是多少万台?
5
4
解:设上半年生产x万台,则下半
年生产
x万台。
x+
x=108
x=108
x=48
108-48=60(万台)
4
5
4
5
4
9
三、巩固练习,提升认识
上衣和裤子各多少钱?
2.
上衣价钱:
裤子价钱:
“1”
?元
?元
300元
上衣价钱+裤子价钱=300元
预设1:
这套运动服共300元。
裤子价钱是上衣的
。
3
2
解:设上衣的价钱为x元,则裤
子的价钱为
x元。
x+
x=300
x=300
x=180
180
×
=120(元)
3
2
3
2
3
5
3
2
上衣价钱:
裤子价钱:
“1”
?元
?元
300元
三、巩固练习,提升认识
如果把裤子的价钱看作是单位“1”,那么上衣的价钱是裤子的几分之几?应该怎样设未知数?
问题:
上衣价钱+裤子价钱=300元
预设2:
上衣和裤子各多少钱?
2.
解:设裤子的价钱为x元,则上
衣的价钱为
x元。
x+
x=300
x=300
x=120
300-120=180(元)
2
3
2
3
2
5
这套运动服共300元。
裤子价钱是上衣的
。
3
2
分数除法
例1
分数除以整数
例2
一个数除以分数
例3
分数混合运算
一、复习导入
说出下面各数的倒数。
4
5
1
7
3
5
11
1
4
1
5
11
5
1
3
7
二、教学例1
分数除以整数
把一张纸的
平均分成2份,每份是这张纸的几分之几?
5
4
2.
请看上面的问题,和我们以前学过的什么知识有关系?(平均分,
求一份是多少)
你能列出算式吗?(
÷2)
5
4
问题:1.
你能用阴影表示出这张纸的
吗?(学生画出长方形纸的
)
5
4
5
4
3.
借助手中的学具,折一折,画一画,表示出
÷2
的意义。
5
4
(一)引入情境,探究新知
问题:1.
用算式表示出刚才折或画的过程。
2.
结合画好的图,说说你的计算过程。
把一张纸的
平均分成2份,每份是这张纸的几分之几?
5
4
5
4
÷2=
=
5
4÷2
5
2
5
4
÷2=
×
=
=
5
2
5
4
2
1
10
4
二、教学例1
分数除以整数
(一)引入情境,探究新知
(二)自主操作,深入理解
2.
用算式表示出刚才折或画的过程。
4.
比较两种解法,你有什么想法?
3.
结合画好的图,说说你的计算过程。
(出示预设1时)你遇到了什么问题?
5.
根据上面的折纸实验和算式,你能发现什么规律?
(出示预设2)说说你的想法。
把一张纸的
平均分成3份,每份是这张纸的几分之几?
5
4
预设1:
5
4
÷3=
=?
5
4÷3
预设2:
5
4
÷3=
×
=
5
4
3
1
15
4
问题:1.
借助手中的学具,折一折,画一画,表示出
÷3
的意义。
5
4
二、教学例1
分数除以整数
计算下面各题。
(三)巩固练习
10
9
÷3=
×
=
(
)
(
)
(
)
(
)
(
)
(
)
9
10
1
3
3
10
8
3
÷2=
×
=
(
)
(
)
(
)
(
)
(
)
(
)
3
8
1
2
3
16
二、教学例1
分数除以整数
(一)引入情境,探究新知
问题:1.
你读懂了什么?想到了什么?请你根据信息画出线段图。
2.
要想比谁走得快,我们可以比什么?
预设1:比较平均每小时走的路程
预设2:比较走1km所用的时间(本课时先解决预设1,预设2可机动)
小明
小时走了2km,
3
2
小红
小时走了
km。谁
走得快些?
12
5
6
5
2km
3
2
小时
三、教学例2
分数除以整数
(二)自主操作,深入理解
解决预设1:小明平均每小时走多少km?
2.
思考,在刚才的线段图上如何表示小明1小时走的路程?
2km
3
2
小时
问题:1.
怎样求上面的问题?用到了我们以前学过的什么知识?
(路程÷时间=速度)请你列出算式。(
)
2÷
3
2
三、教学例2
分数除以整数
小明平均每小时走多少km?
问题:1.
为什么要把2km平均分成2份?
2.
你是怎么想到要补充1份的?
3.
这部分表示什么?
4.
你能用算式表示出所画的意思吗?
5.
结合线段图,说说你是怎么计算的。
2km
3
2
小时
走多少km?
1小时
3
2
2÷
=2
×
×3=2×
=3
(km)
2
3
2
1
1
1
三、教学例2
分数除以整数
(二)自主操作,深入理解
问题:1.
小红1小时走多少千米呢?根据信息和问题,画出线段图。
2.
根据线段图,列式并计算。
4.
请你比较,谁走得快些?
5.
观察上面两个算式的计算,你发现了什么?(一个数除以分
数,等于乘这个分数的倒数。)
3
2
2÷
=2
×
×3=2×
=3
(km)
2
3
2
1
1
1
÷
=
×
=2(km)
12
5
6
5
6
5
5
12
1
2
1
1
3.
“×
”这一步你是怎样想的,结合线段图说一说。
5
12
三、教学例2
一个数除以分数
(二)自主操作,深入理解
(三)巩固练习
1.
计算下面各题
9
8
24÷
=24
(
)
(
)
=(
)
×
9
8
27
5
4
÷
=
16
7
(
)
(
)
(
)
(
)
(
)
(
)
=
7
16
5
4
×
35
64
三、教学例2
一个数除以分数
(一)理解情境,解决问题
四、教学例3
分数乘除混合运算
3.
(出示方法一)谁读懂了它的意思?说一说。
4.
(出示方法二)谁读懂了它的意思?说一说。
问题:1.
你知道了什么?
2.
你能解决这个问题吗?用算式表达你的思考过程。
5.
上面的两种方法,请你用综合算式表示,并写出计算过程。
方法1:
×3
2
1
=
(片)
2
3
12÷
=12×
=8(天)
2
3
3
2
方法2:
12÷
=12×
=24(次)
2
1
1
2
24÷3=8(天)
3.
谁读懂了它的意思,说一说。
问题:1.
你知道了什么?
2.
你能解决这个问题吗?用算式表达你的思考过程。
(二)巩固练习
王叔叔家阁楼上的窗玻璃是梯形的,上底、
下底和高分别是
m、
m、
m。这块玻璃的
面积是多少?
5
3
5
4
4
3
5
3
(
+
)×
÷2
5
4
4
3
=
×
×
5
7
4
3
2
1
=
(
)
40
21
四、教学例3
分数乘除混合运算
五、布置作业
作业:第35页练习七,第7题、第8题。
分数除法
例4
已知一个数的几分之几
是多少求这个数
一、复习导入
阅读下面的句子,说说你的理解。
1.
男生人数占全班人数的
。
5
2
问题:1.
你知道了什么?(男生人数与全班人数比较:全班人数是
单位“1”,男生人数占全班人数的
。)
5
2
5
2
男生
“1”
2.
你还能想到什么?(女生人数占全班人数的
,男生人数
是女生人数的
,女生人数是男生人数的
,……)
5
3
3
2
2
3
二、引入情境,探究新知
(一)收集信息,明确条件问题
小明重多少千克?
问题:你知道了什么?(小明体内的水分重28kg,小明体内的水分占体重
的
,要求的是小明的体重。)
5
4
二、引入情境,探究新知
(二)画图分析,理解数量关系
根据题目的意思,画出线段图。
3.
成人的信息与问题有关系吗?
5
4
水分占体重的
水分28kg
体重?kg
问题:1.
看图,说明图意。(小明身体中水分的重量与体重做比较:小明的体
重是单位“1”,小明体内的水分占体重的
,求小明的体重是多少kg)
5
4
2.
你能列出一个等量关系吗?(小明的体重×
=小明体内水分的质量)
5
4
二、引入情境,探究新知
问题:1.
谁能结合线段图说说对这种解法的理解?
(三)读懂过程,感悟不同方法
2.
你还有其他的解法吗?
预设1:
预设2:
预设3:
解:设小明的体重是x
kg。
x=28
5
4
x=28÷
5
4
x=28×
4
5
x=35
=28÷
5
4
=28×
4
5
=35(kg)
28÷4×5
=7×5
=35(kg)
二、引入情境,探究新知
(四)回顾反思,沟通不同方法
2.
这些不同的算法中有什么相同点与不同点?(单位“1”
相同,数量之间的关系相同。)
解:设小明的体重是x
kg。
x=28
5
4
x=28÷
5
4
x=28×
4
5
x=35
=28÷
5
4
=28×
4
5
=35(kg)
28÷4×5
=7×5
=35(kg)
问题:1.
怎样检验结果是否正确?(35×
=28(kg))
5
4
1.
一杯约250mL的鲜牛奶大约含有
g的钙质,占一个成年人一天
所需钙质的
。一个成年人一天大约需要多少钙质?
4.
你还有别的方法吗?交流与反馈。
问题:1.
你知道了什么?
2.
根据题意画出线段图。
三、巩固练习,提升认识
3.
写出等量关系,列方程解决问题。
10
3
8
3
10
3
预设1:
解:设成年人一天大约需要x
g钙质。
5
4
x=
8
3
x=
÷
8
3
x=
×
x=
10
3
3
8
10
3
预设2:
5
4
÷
8
3
=
×
=
(g)
10
3
3
8
10
3
三、巩固练习,提升认识
16千米/时
2.自行车的速度是摩托车的
,摩托车每小时行多少千米?
5
2
预设1:
解:设摩托车每小时行x千米。
x=16
5
2
x=16÷
5
2
x=16×
x=40
2
5
预设2:
16÷
5
2
=16×
=40(千米)
2
5
问题:1.
你知道了什么?根据题意画出线段图。
2.
你画的线段图和前两道题有什么不同?
4.
谁读懂了它的意思,说一说。还有不同的想法吗?
3.
你能解决这个问题吗?写出你的思考过程。
三、巩固练习,提升认识
3.
(1)图书馆共有多少本书?
(2)图书馆有多少本故事书?
问题:1.
你知道了什么?
2.
解决“图书馆共有多少本书”需要哪个条件?
“图书馆有多少本故事书”呢?
三、巩固练习,提升认识
4.
解决类似的问题,我们要注意什么?(找准和问题对应的条件)
3.
你会解决这两个问题吗?
问题:
(1)图书馆共有多少本书?
(2)图书馆有多少本故事书?
(1)解:设图书馆共有x
本书。
x=320
5
2
x=320÷
5
2
x=320×
x=800
2
5
(2)解:设图书馆共有故事书x
本。
x=320
3
4
x=320÷
3
4
x=320×
x=240
4
3
3.
四、布置作业
作业:第39页练习八,第3题。
分数除法
例5
已知比一个数多(少)
几分之几是多少求这个数
一、复习导入,揭示课题
看图回答问题
问题:
①从图中你知道了什么?
女生人数
男生人数
4
1
多
“1”
②怎样理解“男生人数比女生人数多
”?
(男生人数与女生人数比较;女生人数是单位“1”;把女生人数
平均分成4份,男生人数是(4+1)份。)
4
1
③你能说说男、女生人数之间有怎样的等量关系?
(女生人数×(1+
)=男生人数。)
4
1
二、引入情境,探究新知
(一)阅读与理解
问题:
①从题目中你知道了什么?
③这道题怎样解答,请你根据题意先画出线段图,再找出爸爸
体重和小明体重之间的等量关系,最后列方程解答。
小明的体重是35kg,他的体重比爸爸的体重轻
,
小明爸爸的体重是多少千克?
15
8
②怎样理解“小明的体重比爸爸的体重轻
”?
(小明体重和爸爸体重在比较;爸爸的体重是“1”;把爸爸
体重平均分成15份,小明的体重就是(15-8)份;小明的
体重是爸爸体重的(1-
)。)
15
8
15
8
二、引入情境,探究新知
(二)分析与解答
爸爸的体重-小明比爸爸轻的部分=小明的体重
小明:
预设1:
爸爸:
“1”
小明的体重比爸爸轻
?千克
是爸爸体重的几分之几?
35千克
问题:
①你们能借助线段图理解这个等量关系式和方程的意思吗?
②图中哪部分是小明体重比爸爸轻的部分?
③他是怎样求小明体重比爸爸轻的部分的?
解:设爸爸的体重为x
kg。
x-
x=35
x=35
x=35×
x=75
15
8
15
7
7
15
二、引入情境,探究新知
(二)分析与解答
预设2:
小明的体重比爸爸轻
?千克
35千克
爸爸:
小明:
“1”
是爸爸体重的几分之几?
问题:
①你们能借助线段图理解这个数量关系式和方程的意思吗?
②图中小明的体重相当于爸爸体重的哪一部分?
③小明的体重相当于爸爸体重的几分之几?你是怎样得到的?
爸爸的体重×(1-
)=小明的体重
15
8
解:设爸爸的体重为x
kg。
(1-
)x=35
x=35
x=35×
x=75
15
8
15
7
7
15
二、引入情境,探究新知
(二)分析与解答
小结:
虽然两种解法不同,但是都是依据分数乘法的意义找到等量关系,用方程解答。
爸爸的体重-小明比爸爸轻的部分
=小明的体重
解:设爸爸的体重为x
kg。
x-
x=35
x=35
x=35×
x=75
15
8
15
7
7
15
爸爸的体重×(1-
)=小明的体重
15
8
解:设爸爸的体重为x
kg。
(1-
)x=35
x=35
x=35×
x=75
15
7
7
15
15
8
二、引入情境,探究新知
(三)回顾与反思
问题:
刚才同学们用两种不同的方法求出了爸爸的体重,那么对不对呢?都可以怎样检查?
15
7
预设1:
看看小明的体重是不是爸爸的
35
÷75
=
15
7
预设2:
看看小明的体重是不是比爸爸轻
(75-35
)÷75
=
15
8
15
8
看看小明的体重是不是35千克
预设3:
75
×(1-
)=35
15
8
三、巩固练习,提升认识
“1”
还剩
读了35页
?页
1.
这本课外读物一共有多少页?
这本课外读物我读了35页,还剩下
没读。
7
2
预设1:
解:设这本课外读物一共有x页。
x-
x=35
x=35
x=49
7
2
7
5
预设2:
解:设这本课外读物一共有x页。
(1-
)x=35
x=35
x=49
7
2
7
5
三、巩固练习,提升认识
30人
?人
“1”
篮球队人数:
足球队人数:
多
2.
学校足球队一共有30人,比篮球队的人数多
,篮球队有多少人?
5
1
解:设篮球队有x人。
x+
x=30
x=30
x=25
预设1:
5
1
5
6
预设2:
解:设篮球队有x人。
(1
+
)x=30
x=30
x=25
5
1
5
6
四、布置作业
作业:第47页练习十,第4题。
分数除法
例6
两个未知数的和倍问题
一、复习导入,揭示课题
看图回答问题
问题:
①从图中你知道了什么?
女生人数
男生人数
②根据线段图,你能说说男、女生人数间的数量关系吗?
(男生人数与女生人数比较;女生人数是单位“1”;把女生人数平
均分成4份,男生人数是5份;男生人数是女生人数的
。
女生人数与男生人数比较;男生人数是单位“1”;把男生人数平均
分成5份,女生人数是4份;女生人数是男生人数的
。)
4
5
5
4
③如果男生有x人,女生有多少人?你是怎样得到的?(女生
x人。)
如果女生有x人,男生有多少人?你是怎样得到的?(男生
x人。)
5
4
4
5
二、引入情境,探究新知
(一)阅读与理解
问题:
①从题目中你知道了什么?
③这道题怎样解答,请你根据题意画出线段图。
上半场和下半场各得多少分?
②怎样理解“下半场得分只有上半场的一半”这句话?
(下半场得分和上半场得分在比较;上半场得分看作单位“1”;
下半场得分是上半场的
。)
2
1
二、引入情境,探究新知
(二)分析与解答
问题:
①你们能借助线段图找出一个等量关系式吗?
②上半场和下半场的得分我们都不知道,那怎样设未知数?
(上半场得分+下半场得分=42分)
③请你依据等量关系列方程并解答。
上半场得分:
下半场得分:
“1”
?分
?分
2
1
42分
预设1:
解:设上半场得了x分,则下半场
得了
x分。
x+
x=42
x=42
x=42×
x=28
28×
=14(分)
2
1
2
1
2
3
3
2
2
1
二、引入情境,探究新知
(二)分析与解答
解:设下半场得了x分,则上半场
得了2x分。
x+2x=42
3x=42
x=42
÷3
x=14
42-14=28(分)
问题:
①如果设下半场得了x分,那么我们把谁看作是单位“1”?
②如果把下半场得分看作单位“1”,那么上半场得分是下半场的几倍?
③应该怎样设未知数?说说你列的方程。
(上半场得分+下半场得分=42分)
预设2:
“1”
上半场得分:
下半场得分:
42分
?分
?分
2倍
二、引入情境,探究新知
问题:
我们依据题意画出了相同的线段图,找到了相同的等量关系,为什么同学们列出的方程不一样呢?
(上半场得分+下半场得分=42分)
(上半场得分+下半场得分=42分)
解:设上半场得了x分,则下半场
得了
x分。
x+
x=42
x=42
x=42×
x=28
28×
=14(分)
2
1
2
1
2
3
3
2
2
1
解:设下半场得了x分,则上半场
得了2x分。
x+2x=42
3x=42
x=42
÷3
x=14
42-14=28(分)
(二)分析与解答
二、引入情境,探究新知
(三)回顾与反思
问题:
刚才同学们列出了两个不同的方程,分别求出了上、下半场的得分,那么对不对呢?可以怎样检验?
预设1:
看看上、下半场的得分和是不是42分
28
+14
=42(分)
预设2:
看看下半场得分是不是上半场的
14÷28
=
2
1
2
1
三、巩固练习,提升认识
108万台
“1”
下半年产量:
上半年产量:
?万台
?万台
上半年产量+下半年产量=全年产量
预设1:
1.
某电视厂去年全年生产电视机108万台,其中上
半年产量是下半年的
。这个电视机厂去年上
半年和下半年的产量分别是多少万台?
5
4
解:设下半年生产x万台,则上
半年生产
x万台。
x+
x=108
x=108
x=60
60
×
=48(万台)
5
4
5
4
5
9
5
4
三、巩固练习,提升认识
如果把上半年的产量看作是单位“1”那么下半年的产量是上半年的几分之几?应该怎样设未知数?
问题:
上半年产量+下半年产量=全年产量
预设2:
108万台
“1”
下半年产量:
上半年产量:
?万台
?万台
1.
某电视厂去年全年生产电视机108万台,其中上
半年产量是下半年的
。这个电视机厂去年上
半年和下半年的产量分别是多少万台?
5
4
解:设上半年生产x万台,则下半
年生产
x万台。
x+
x=108
x=108
x=48
108-48=60(万台)
4
5
4
5
4
9
三、巩固练习,提升认识
上衣和裤子各多少钱?
2.
上衣价钱:
裤子价钱:
“1”
?元
?元
300元
上衣价钱+裤子价钱=300元
预设1:
这套运动服共300元。
裤子价钱是上衣的
。
3
2
解:设上衣的价钱为x元,则裤
子的价钱为
x元。
x+
x=300
x=300
x=180
180
×
=120(元)
3
2
3
2
3
5
3
2
上衣价钱:
裤子价钱:
“1”
?元
?元
300元
三、巩固练习,提升认识
如果把裤子的价钱看作是单位“1”,那么上衣的价钱是裤子的几分之几?应该怎样设未知数?
问题:
上衣价钱+裤子价钱=300元
预设2:
上衣和裤子各多少钱?
2.
解:设裤子的价钱为x元,则上
衣的价钱为
x元。
x+
x=300
x=300
x=120
300-120=180(元)
2
3
2
3
2
5
这套运动服共300元。
裤子价钱是上衣的
。
3
2
