北师大版 七年级数学下册试题 第五章 生活中的轴对称 单元复习卷(Word版 含答案)
文档属性
| 名称 | 北师大版 七年级数学下册试题 第五章 生活中的轴对称 单元复习卷(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 516.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 09:56:36 | ||
图片预览



文档简介
第五单元复习卷
一、选择题
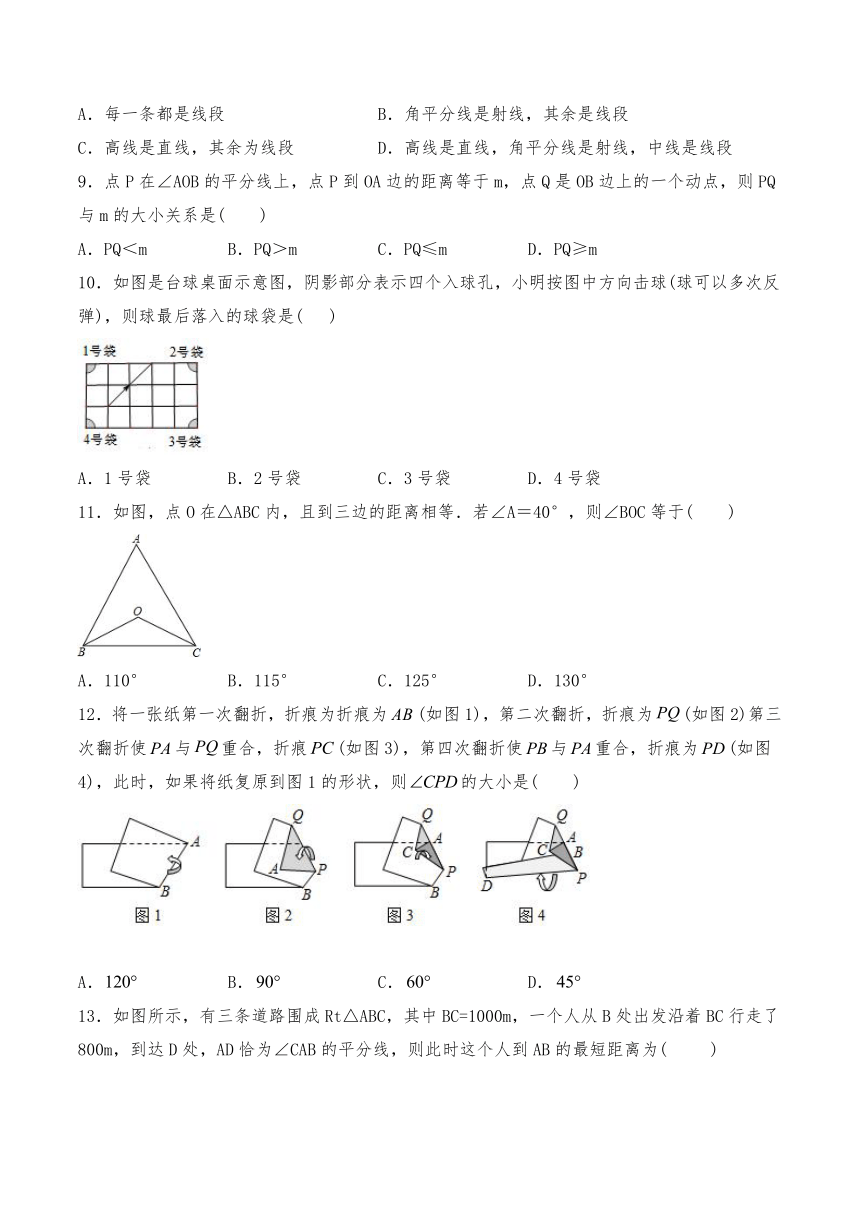
1.永州市教育部门高度重视校园安全教育,要求各级各类学校从认识安全警告标志入手开展安全教育,下列安全图标不是轴对称的是(
)
A.注意安全
B.水深危险
C.必须戴安全帽
D.注意通风
2.小明从平面镜里看到镜子对面电子钟的示数的像如图所示,这时的时刻应是(?
?
?
?
)
A.
B.
C.
D.
3.如图,已知与关于直线l对称,,则的度数为(
)
A.
B.
C.
D.
4.利用一张左、右两边已经破损的长方形纸片折纸,如图,将纸片沿折叠后,、两点分别落在、的位置,若,则的度数为(
)
A.
B.
C.
D.
5.如图①,已知,用尺规作它的角平分线(如图②).
尺规作图具体步骤如下,
第1步:以为圆心,以为半径画弧,分别交射线于点;
第2步:分别以为圆心,以为半径画弧,两弧在内部交于点;
第3步:画射线.射线即为所求.
下列说法正确的是(
)
A.有最小限制,无限制
B.的长
C.的长
D.连接,则垂直平分
6.如图,在△ABC中,∠C=90°,BD平分∠ABC,若CD=3,则点D到AB的距离为(
)
A.4
B.3
C.2.5
D.5
7.三条相互交叉的公路,现要建一个货物转运站,要求它到三条公路的距离相等,则可供选择的地址有(
).
A.1个
B.2个
C.3个
D.4个
8.三角形的角平分线、中线、高线(
)
A.每一条都是线段
B.角平分线是射线,其余是线段
C.高线是直线,其余为线段
D.高线是直线,角平分线是射线,中线是线段
9.点P在∠AOB的平分线上,点P到OA边的距离等于m,点Q是OB边上的一个动点,则PQ与m的大小关系是( )
A.PQ<m
B.PQ>m
C.PQ≤m
D.PQ≥m
10.如图是台球桌面示意图,阴影部分表示四个入球孔,小明按图中方向击球(球可以多次反弹),则球最后落入的球袋是(
)
A.1号袋
B.2号袋
C.3号袋
D.4号袋
11.如图,点O在△ABC内,且到三边的距离相等.若∠A=40°,则∠BOC等于( )
A.110°
B.115°
C.125°
D.130°
12.将一张纸第一次翻折,折痕为折痕为(如图1),第二次翻折,折痕为(如图2)第三次翻折使与重合,折痕(如图3),第四次翻折使与重合,折痕为(如图4),此时,如果将纸复原到图1的形状,则的大小是(
)
A.
B.
C.
D.
13.如图所示,有三条道路围成Rt△ABC,其中BC=1000m,一个人从B处出发沿着BC行走了800m,到达D处,AD恰为∠CAB的平分线,则此时这个人到AB的最短距离为(
)
A.1000m
B.800m
C.200m
D.1800m
14.如图,长方形纸片,将沿对角线折叠得,和相交于点E,将沿折叠得,若,则度数为(
)
A.
B.
C.
D.
二、填空题
15.如图,在3×3正方形网格中,黑色部分的图形构成一个轴对称图形,若在其余网格中再涂黑一个小正方形,使黑色部分的图形仍然构成一个轴对称图形,则可涂黑的小正方形共有______.
16.如图,在矩形中,,一发光电子开始置于边的点处,并设定此时为发光电子第一次与矩形的边碰撞,将发光电子沿着方向发射,碰撞到矩形的边时均反射,每次反射的反射角和入射角都等于45°,若发光电子与矩形的边碰撞次数经过2021次后,则它与边的碰撞次数是_________.
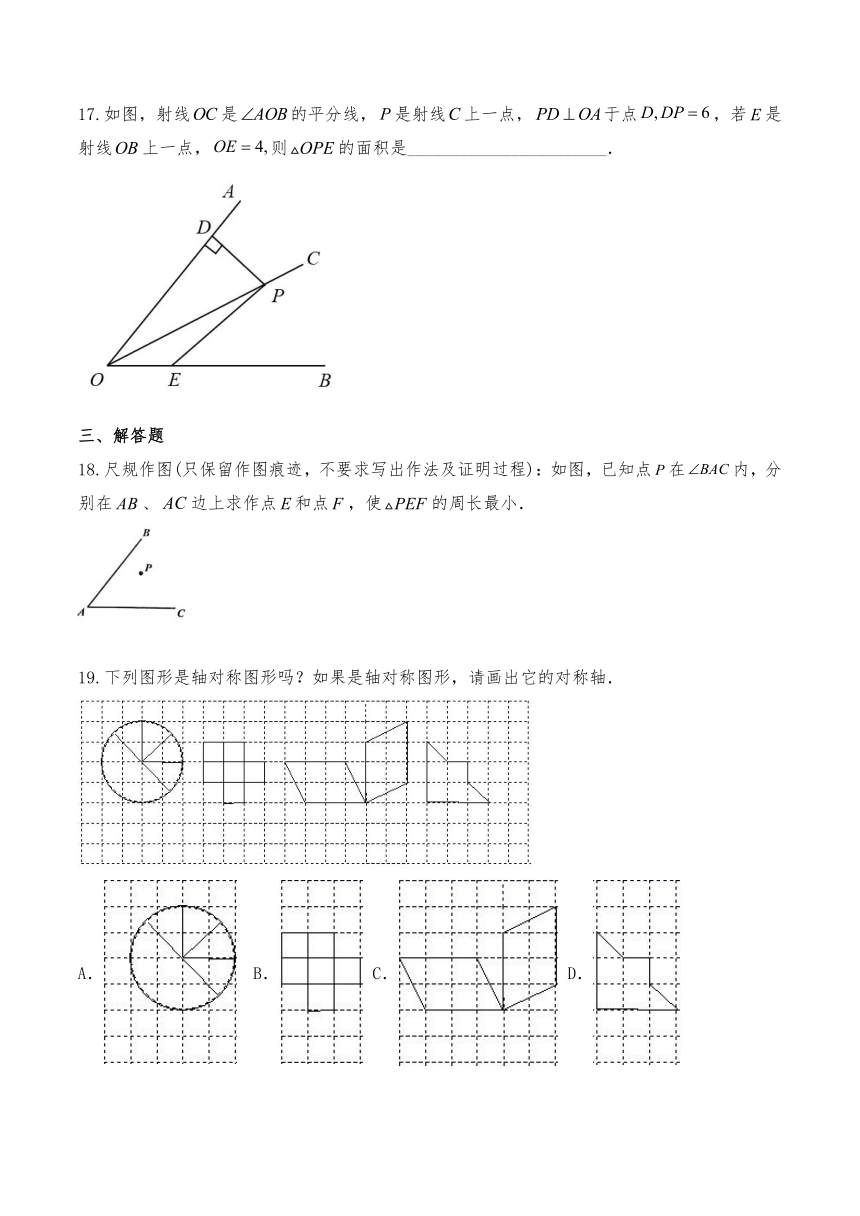
17.如图,射线是的平分线,是射线上一点,于点,若是射线上一点,则的面积是_______________________.
三、解答题
18.尺规作图(只保留作图痕迹,不要求写出作法及证明过程):如图,已知点在内,分别在、边上求作点和点,使的周长最小.
19.下列图形是轴对称图形吗?如果是轴对称图形,请画出它的对称轴.
A.
B.
C.
D.
20.小河AB的同旁有甲、乙两个村庄,现计划在河岸AB上建一个水泵站,向两村供水,用以解决村民生活用水问题.若要求水泵站到甲、乙两村庄的距离之和最小,水泵站M应建在河岸AB上的何处?(要求:不写作法,但要保留作图痕迹,并写出作图结果)
21.已知长方形纸片ABCD,点E在边AB上,点F、G在边CD上,连接EF、EG,将∠BEG对折,点B落在直线EG上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN.
(1)如图1,若点F与点G重合,求∠MEN的度数;
(2)如图2,若点G在点F的右侧,且∠FEG=30°,求∠MEN的度数;
22.如图,已知在一张纸条上画有一条数轴.
(1)沿过原点且垂直于数轴的直线折叠纸条,则表示-3的点与表示___________的点重合;
(2)为数轴上一点,沿过点且垂直于数轴的直线折叠纸条,当表示-3的点与表示1的点重合时,
①点所表示的数为__________;
②若数轴上的,两点也同时重合,且,求点所表示的数.
23.如图,在△ABC中,AB=AC,D,E是BC边上的点,连接AD,AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD'E,连接D'C,若BD=CD'.
(1)求证:△ABD≌△ACD'.
(2)若∠BAC=100°,求∠DAE的度数.
24.生活中,有人喜欢把传送的便条折成“”形状,折叠过程按图①?②?③?④的顺序进行(其中阴影部分表示纸条的反面):
如果由信纸折成的长方形纸条(图①)长为26厘米,分别回答下列问题:
(1)如果长方形纸条的宽为2厘米,并且开始折叠时起点与点的距离为3厘米,那么在图②中,__________厘米;在图③中,__________厘米;在图④中,__________厘米.
(2)如果长方形纸条的宽为厘米,现不但要折成图④的形状,而且为了美观,希望纸条两端超出点的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点与点的距离(结果用表示).
25.已知是的平分线,点是射线上一点,点C、D分别在射线、上,连接PC、PD.
(1)发现问题
如图①,当,时,则PC与PD的数量关系是________.
(2)探究问题
如图②,点C、D在射线OA、OB上滑动,且∠AOB=90°,∠OCP+∠ODP=180°,当时,PC与PD在(1)中的数量关系还成立吗?说明理由.
答案
一、选择题
1.D.2.D.3.B.4.A.5.B.6.B7.D.8.A.9.D.10.B.
11.A.12.B.13.C.14.C.
二、填空题
15.4.
16.674
17.12
三、解答题
18.解:如图:即为所求,
注:①作关于的对称点;
②作关于的对称点;
③连接P1P2.
④P1P2与AB的交点就是E,P1P2与BC的交点就是F.
19.图案C不是轴对称图形,图案A、B、D都是轴对称图形,对称轴如图所示:
20.根据题意画出如下图所示,图中的点即为水泵站的位置:
21.解:(1)∵EN平分∠AEF,EM平分∠BEF
∴∠NEF=∠AEF,∠MEF=∠BEF
∴∠MEN=∠NEF+∠MEF=∠AEF+∠BEF=(∠AEF+∠BEF)=∠AEB
∵∠AEB=180°
∴∠MEN=×180°=90°
(2)∵EN平分∠AEF,EM平分∠BEG
∴∠NEF=∠AEF,∠MEG=∠BEG
∴∠NEF+∠MEG=∠AEF+∠BEG=(∠AEF+∠BEG)=(∠AEB﹣∠FEG)
∵∠AEB=180°,∠FEG=30°
∴∠NEF+∠MEG=(180°﹣30°)=75°
∴∠MEN=∠NEF+∠FEG+∠MEG=75°+30°=105°.
22.解:(1)沿过原点且垂直于数轴的直线折叠纸条,则表示-3的点与表示3的点重合;
故答案为:3;
(2)①∵表示-3的点与表示1的点重合,
∴点表示的数是.
②∵,点表示的数是-1,
∴点表示的数是或.
23.解:(1)以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△A,
在△ABD与中,
(2)
,∠BAC==100°,
以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△A,
∠DAE.
24.解:(1)图②中BE=AB-AM-EM=26-3-2=21厘米,
图③中BF=26-3-2-2=19?厘米,
图④中BM=26-3-2-2-2-2=15厘米,
故答案为:21;19;15;
(2)因为图④为轴对称图形
所以,,
即开始折叠时点M与点A的距离是(13?x)厘米.
25.解:(1)∵OM是∠AOB的平分线,PC⊥OA,PD⊥OB,
∴PC=PD,
故答案为:PC=PD;
(2)PC=PD仍然成立.理由如下:
过P分别作PE⊥OB于E,PF⊥OA于F,
∴∠CFP=∠DEP=90°,
∵OM是∠AOB的平分线,∴PE=PF.
∵∠OCP+∠ODP=180°,又∠ODP+∠PDE=180°,
∴∠OCP=∠PDE,即∠FCP=∠PDE,
在△CFP和△DEP中,
,
∴△CFP≌△DEP(AAS),
∴PC=PD.
一、选择题
1.永州市教育部门高度重视校园安全教育,要求各级各类学校从认识安全警告标志入手开展安全教育,下列安全图标不是轴对称的是(
)
A.注意安全
B.水深危险
C.必须戴安全帽
D.注意通风
2.小明从平面镜里看到镜子对面电子钟的示数的像如图所示,这时的时刻应是(?
?
?
?
)
A.
B.
C.
D.
3.如图,已知与关于直线l对称,,则的度数为(
)
A.
B.
C.
D.
4.利用一张左、右两边已经破损的长方形纸片折纸,如图,将纸片沿折叠后,、两点分别落在、的位置,若,则的度数为(
)
A.
B.
C.
D.
5.如图①,已知,用尺规作它的角平分线(如图②).
尺规作图具体步骤如下,
第1步:以为圆心,以为半径画弧,分别交射线于点;
第2步:分别以为圆心,以为半径画弧,两弧在内部交于点;
第3步:画射线.射线即为所求.
下列说法正确的是(
)
A.有最小限制,无限制
B.的长
C.的长
D.连接,则垂直平分
6.如图,在△ABC中,∠C=90°,BD平分∠ABC,若CD=3,则点D到AB的距离为(
)
A.4
B.3
C.2.5
D.5
7.三条相互交叉的公路,现要建一个货物转运站,要求它到三条公路的距离相等,则可供选择的地址有(
).
A.1个
B.2个
C.3个
D.4个
8.三角形的角平分线、中线、高线(
)
A.每一条都是线段
B.角平分线是射线,其余是线段
C.高线是直线,其余为线段
D.高线是直线,角平分线是射线,中线是线段
9.点P在∠AOB的平分线上,点P到OA边的距离等于m,点Q是OB边上的一个动点,则PQ与m的大小关系是( )
A.PQ<m
B.PQ>m
C.PQ≤m
D.PQ≥m
10.如图是台球桌面示意图,阴影部分表示四个入球孔,小明按图中方向击球(球可以多次反弹),则球最后落入的球袋是(
)
A.1号袋
B.2号袋
C.3号袋
D.4号袋
11.如图,点O在△ABC内,且到三边的距离相等.若∠A=40°,则∠BOC等于( )
A.110°
B.115°
C.125°
D.130°
12.将一张纸第一次翻折,折痕为折痕为(如图1),第二次翻折,折痕为(如图2)第三次翻折使与重合,折痕(如图3),第四次翻折使与重合,折痕为(如图4),此时,如果将纸复原到图1的形状,则的大小是(
)
A.
B.
C.
D.
13.如图所示,有三条道路围成Rt△ABC,其中BC=1000m,一个人从B处出发沿着BC行走了800m,到达D处,AD恰为∠CAB的平分线,则此时这个人到AB的最短距离为(
)
A.1000m
B.800m
C.200m
D.1800m
14.如图,长方形纸片,将沿对角线折叠得,和相交于点E,将沿折叠得,若,则度数为(
)
A.
B.
C.
D.
二、填空题
15.如图,在3×3正方形网格中,黑色部分的图形构成一个轴对称图形,若在其余网格中再涂黑一个小正方形,使黑色部分的图形仍然构成一个轴对称图形,则可涂黑的小正方形共有______.
16.如图,在矩形中,,一发光电子开始置于边的点处,并设定此时为发光电子第一次与矩形的边碰撞,将发光电子沿着方向发射,碰撞到矩形的边时均反射,每次反射的反射角和入射角都等于45°,若发光电子与矩形的边碰撞次数经过2021次后,则它与边的碰撞次数是_________.
17.如图,射线是的平分线,是射线上一点,于点,若是射线上一点,则的面积是_______________________.
三、解答题
18.尺规作图(只保留作图痕迹,不要求写出作法及证明过程):如图,已知点在内,分别在、边上求作点和点,使的周长最小.
19.下列图形是轴对称图形吗?如果是轴对称图形,请画出它的对称轴.
A.
B.
C.
D.
20.小河AB的同旁有甲、乙两个村庄,现计划在河岸AB上建一个水泵站,向两村供水,用以解决村民生活用水问题.若要求水泵站到甲、乙两村庄的距离之和最小,水泵站M应建在河岸AB上的何处?(要求:不写作法,但要保留作图痕迹,并写出作图结果)
21.已知长方形纸片ABCD,点E在边AB上,点F、G在边CD上,连接EF、EG,将∠BEG对折,点B落在直线EG上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN.
(1)如图1,若点F与点G重合,求∠MEN的度数;
(2)如图2,若点G在点F的右侧,且∠FEG=30°,求∠MEN的度数;
22.如图,已知在一张纸条上画有一条数轴.
(1)沿过原点且垂直于数轴的直线折叠纸条,则表示-3的点与表示___________的点重合;
(2)为数轴上一点,沿过点且垂直于数轴的直线折叠纸条,当表示-3的点与表示1的点重合时,
①点所表示的数为__________;
②若数轴上的,两点也同时重合,且,求点所表示的数.
23.如图,在△ABC中,AB=AC,D,E是BC边上的点,连接AD,AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD'E,连接D'C,若BD=CD'.
(1)求证:△ABD≌△ACD'.
(2)若∠BAC=100°,求∠DAE的度数.
24.生活中,有人喜欢把传送的便条折成“”形状,折叠过程按图①?②?③?④的顺序进行(其中阴影部分表示纸条的反面):
如果由信纸折成的长方形纸条(图①)长为26厘米,分别回答下列问题:
(1)如果长方形纸条的宽为2厘米,并且开始折叠时起点与点的距离为3厘米,那么在图②中,__________厘米;在图③中,__________厘米;在图④中,__________厘米.
(2)如果长方形纸条的宽为厘米,现不但要折成图④的形状,而且为了美观,希望纸条两端超出点的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点与点的距离(结果用表示).
25.已知是的平分线,点是射线上一点,点C、D分别在射线、上,连接PC、PD.
(1)发现问题
如图①,当,时,则PC与PD的数量关系是________.
(2)探究问题
如图②,点C、D在射线OA、OB上滑动,且∠AOB=90°,∠OCP+∠ODP=180°,当时,PC与PD在(1)中的数量关系还成立吗?说明理由.
答案
一、选择题
1.D.2.D.3.B.4.A.5.B.6.B7.D.8.A.9.D.10.B.
11.A.12.B.13.C.14.C.
二、填空题
15.4.
16.674
17.12
三、解答题
18.解:如图:即为所求,
注:①作关于的对称点;
②作关于的对称点;
③连接P1P2.
④P1P2与AB的交点就是E,P1P2与BC的交点就是F.
19.图案C不是轴对称图形,图案A、B、D都是轴对称图形,对称轴如图所示:
20.根据题意画出如下图所示,图中的点即为水泵站的位置:
21.解:(1)∵EN平分∠AEF,EM平分∠BEF
∴∠NEF=∠AEF,∠MEF=∠BEF
∴∠MEN=∠NEF+∠MEF=∠AEF+∠BEF=(∠AEF+∠BEF)=∠AEB
∵∠AEB=180°
∴∠MEN=×180°=90°
(2)∵EN平分∠AEF,EM平分∠BEG
∴∠NEF=∠AEF,∠MEG=∠BEG
∴∠NEF+∠MEG=∠AEF+∠BEG=(∠AEF+∠BEG)=(∠AEB﹣∠FEG)
∵∠AEB=180°,∠FEG=30°
∴∠NEF+∠MEG=(180°﹣30°)=75°
∴∠MEN=∠NEF+∠FEG+∠MEG=75°+30°=105°.
22.解:(1)沿过原点且垂直于数轴的直线折叠纸条,则表示-3的点与表示3的点重合;
故答案为:3;
(2)①∵表示-3的点与表示1的点重合,
∴点表示的数是.
②∵,点表示的数是-1,
∴点表示的数是或.
23.解:(1)以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△A,
在△ABD与中,
(2)
,∠BAC==100°,
以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△A,
∠DAE.
24.解:(1)图②中BE=AB-AM-EM=26-3-2=21厘米,
图③中BF=26-3-2-2=19?厘米,
图④中BM=26-3-2-2-2-2=15厘米,
故答案为:21;19;15;
(2)因为图④为轴对称图形
所以,,
即开始折叠时点M与点A的距离是(13?x)厘米.
25.解:(1)∵OM是∠AOB的平分线,PC⊥OA,PD⊥OB,
∴PC=PD,
故答案为:PC=PD;
(2)PC=PD仍然成立.理由如下:
过P分别作PE⊥OB于E,PF⊥OA于F,
∴∠CFP=∠DEP=90°,
∵OM是∠AOB的平分线,∴PE=PF.
∵∠OCP+∠ODP=180°,又∠ODP+∠PDE=180°,
∴∠OCP=∠PDE,即∠FCP=∠PDE,
在△CFP和△DEP中,
,
∴△CFP≌△DEP(AAS),
∴PC=PD.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
