三角形复习

(共31张PPT)
《三角形》 复习
七年级数学第七章
襄州区城关一中 朱小平
创设情境 引入课题
电线杆
自行车
自我诊断 回顾知识
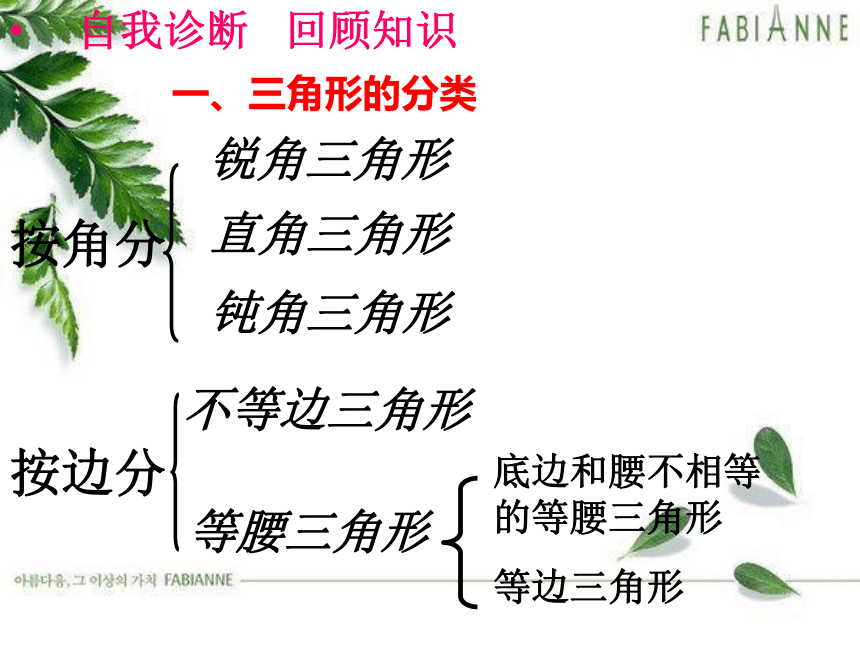
按角分
锐角三角形
直角三角形
钝角三角形
按边分
不等边三角形
等腰三角形
底边和腰不相等的等腰三角形
等边三角形
一、三角形的分类
1.下列长度的三条线段能否组成三角形？为什么？
（1） 3，4，8 （ ）
（2） 2，5，6 （ ）
（3） 5，6，10 （ ）
（4） 3，5，8 （ ）
不能
能
能
不能
二 、与三角形有关的线段
自我诊断 回顾知识
三角形的三边关系
三角形两边之和大于第三边，两边之差小于第三边
试一试
2.若三角形的两边长分别为3和5，则第三边X的取值范围是__________
3.各边长均为整数的三角形周长为12，这样的三角形有______个？各边分别是______________________按边分依次是___________________三角形。
自我诊断 回顾知识
三角形的高线、中线、角平分线定义
1.下列命题正确的是（ ）
A.三角形的中线就是过顶点平分对边的直线。
B.三角形的高线就是顶点到对边的距离。
C.三角形角平分线就是三角形内角的平分线。
D.三角形的三条中线必相交于一点。
二 、与三角形有关的线段
自我诊断 回顾知识
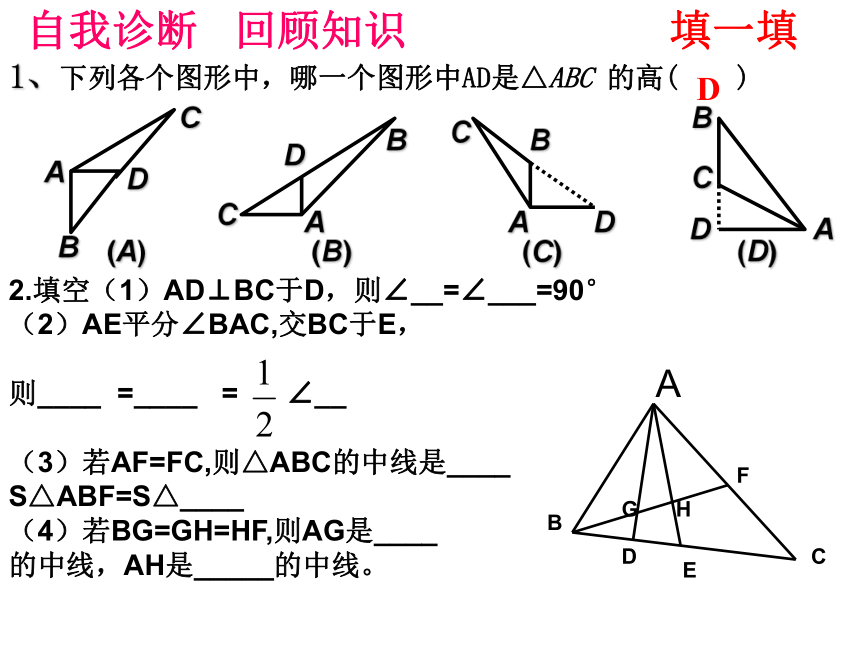
1、下列各个图形中，哪一个图形中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
(A)
(B)
(C)
(D)
填一填
D
2.填空（1）AD⊥BC于D，则∠__=∠___=90°
（2）AE平分∠BAC,交BC于E，
则____ =____ = ∠__
（3）若AF=FC,则△ABC的中线是____
S△ABF=S△____
（4）若BG=GH=HF,则AG是____
的中线，AH是_____的中线。
B
C
E
D
G
F
H
A
自我诊断 回顾知识
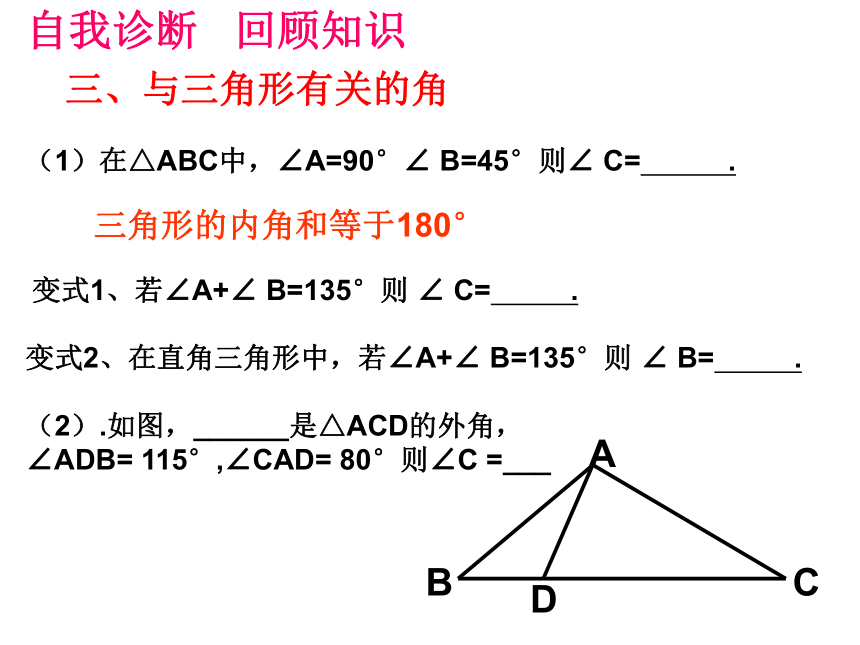
三、与三角形有关的角
（1）在△ABC中，∠A=90°∠ B=45°则∠ C= .
三角形的内角和等于180°
变式1、若∠A+∠ B=135°则 ∠ C= .
变式2、在直角三角形中，若∠A+∠ B=135°则 ∠ B= .
（2）.如图，______是△ACD的外角，
∠ADB= 115°,∠CAD= 80°则∠C =___
A
B
C
D
自我诊断 回顾知识
说一说
1、十二边形的内角和为 ________
2、一个正多边形每一个内角都是120o，这个多边形是（　　）
3、下列图形中能够用来作平面镶嵌的是( ) A.正八边形 B.正七边形 C.正六边形 D.正五边形
多边形的内角和（n-2)180°
多边形的外角和360°
镶嵌
自我诊断 回顾知识
(n-2) ×180°
三角形
与三角形有关的线段
a-b＜c＜a+b（a-b＞0）
高
三角形的边
三角形的三边关系
中线
角平分线的定义
位置、交点
三角形的内角和
多边形的内角和
多边形的外角和
三角形的外角和
多边形外角和为360°
镶嵌的原理
梳理知识 形成体系
三角形的角
三角形的分类
例1.已知等腰三角形的两边长分别为10和6，则三角形的周长为________
变式1：若改为一边长为4，另一边为10，则三 角形的周长为________
变式2：若等腰三角形的周长为18，一边长为8，则其它两边的长为____________
变式3：若等腰三角形的周长为18，一边长为6，则其它两边的长为____________
变式4：若等腰三角形的周长为18，一边长为4，则其它两边的长为____________
变式5：若腰AB=5，底BC=3，BD为一腰上的中线，则△ABC与△BCD的周长之差为__________
变式6：若中线BD将等腰三角形的周长分为15和6两部分，求这个等腰三角形的腰与底。
例题剖析 掌握方法
A
B
C
D
变式6：若中线BD将等腰三角形的周长分为15和6两部分，求这个等腰三角形的腰与底。
A
B
C
D
例题剖析 掌握方法
例2：如图，在△ABC中，∠ABC、∠ACB的平分线BD、CE交于O点.
1、若∠ABC=40°∠ACB=60° 则∠BOC=_____
变式（1）若∠ABC+∠ACB=100°则∠BOC=_____
变式（2）若 ∠A=80°则∠BOC=_____
变式（3）若 ∠BOC=100° 则∠A= ____
变式（4）你能找出∠A与∠BOC 之间的数量关系吗？
A
B
C
D
E
O
例题剖析 掌握方法
变式（4）你能找出∠A与∠BOC 之间的数量关系吗
A
B
C
D
E
O
变式（5）若换成两外角的平分线相交于O,
∠BOC与∠A又有怎样的关系？
A
B
C
D
E
O
变式（6）若换成一内角与一外角的平分线
相交于点O，∠O与∠A又有怎样的关系？
A
B
C
D
E
O
F
O
变式（7）若将△ABC的两条角平分线BD、CE改为高交于O点，∠A与∠BOC又有怎样的关系？
A
O
E
D
C
B
变式训练 提升能力
1.在△ABC中，∠B=40°，∠C=80°AE平分∠BAC,AD⊥BC于D，求∠EAD
变式1：若已知∠C-∠B=20°，求∠EAD
变式2：若∠C＞∠B，请写出∠EAD与∠B、∠C的关系。
A
B
C
D
E
∟
A
B
C
D
E
变式3：当AD移动到FD的位置时，FD⊥BC于D,其它条件不变，∠FDE与∠B、∠C又有怎样的关系？
A
B
C
D
E
F
变式4：将FD继续移到三角形外部，上述结论还成立吗？
A
B
C
D
E
F
D
变式5：若过点D作DG⊥AE于G,∠EDG与∠B,∠C又有怎样的关系？
A
B
C
D
E
G
A
B
C
D
E
G
F
A
E
B
C
D
G
F
1.有人说，自己步子大，一步能走3米多，你相信吗？说说你的理由！
考考你！
答：不能。如果此人一步能走3米多，由三角形三边的关系得，此人两腿得长大于3米多，这与实际情况相矛盾，所以它一步不能走3米多。
利用数学 走进生活
2.小亮从A点出发前进10米，向右转36°……
这样一直走下去，能回到点A 吗？若能，当他第一次回到点A时，一共走了多少米？若不能，说出理由。
A
利用数学 走进生活
归纳小结 布置作业
通过本节课的学习：
你对哪些知识掌握更牢固了？
你对哪些思想方法运用更自如了？
你还有哪些疑惑需要向我倾诉？
归纳小结 布置作业
作业：必做题
1、等腰三角形一边的长是5 cm，另一边的长是8cm，
求它的周长
2.如图, △ABC中, ∠A= ∠ABD,
∠C= ∠BDC= ∠ABC,求∠DBC的度数
A
B
C
D
3.如图1， ∠Ａ＝４５ ∠Ｂ＝２５ ° ∠Ｃ＝３０ °求∠Ｄ
变式2：如图， ∠Ａ＋∠Ｂ＋∠Ｃ＋∠Ｅ＋∠Ｆ=____
Ｂ
Ｃ
Ｄ
Ｅ
Ｅ
Ｅ
Ｆ
Ａ
Ｂ
Ｃ
Ｄ
探究题
有一六边形，截去一三角形，内角和会发生怎样变化？请画图说明。
利用镶嵌知识设计一幅美丽的图案。
兴趣题