1.1.2 探索勾股定理

1.1.2探索勾股定理
姓名：
一、回顾:
（1）勾股定理：
（2）求下列直角三角形的未知边的长
（3）在一个直角三角形中，两条直角边分别为，，斜边为：
如果，，则 ，面积为 ；
如果，，则三角形的周长为 ，面积为 ；
二、导学:（验证勾股定理）
（1）用两种方法求右图网格中所示正方形的面积：
因此，在左图中，4， 9，
通过上面的方法可求得 ，
∴可得
∵， ， ，
∴
（2）请用两种方法表示出如图所示的梯形的面积，由等面积法可验证勾股定理吗
方法一（公式法）：
方法二（看成几部分之和）：
验证：
三、提出问题
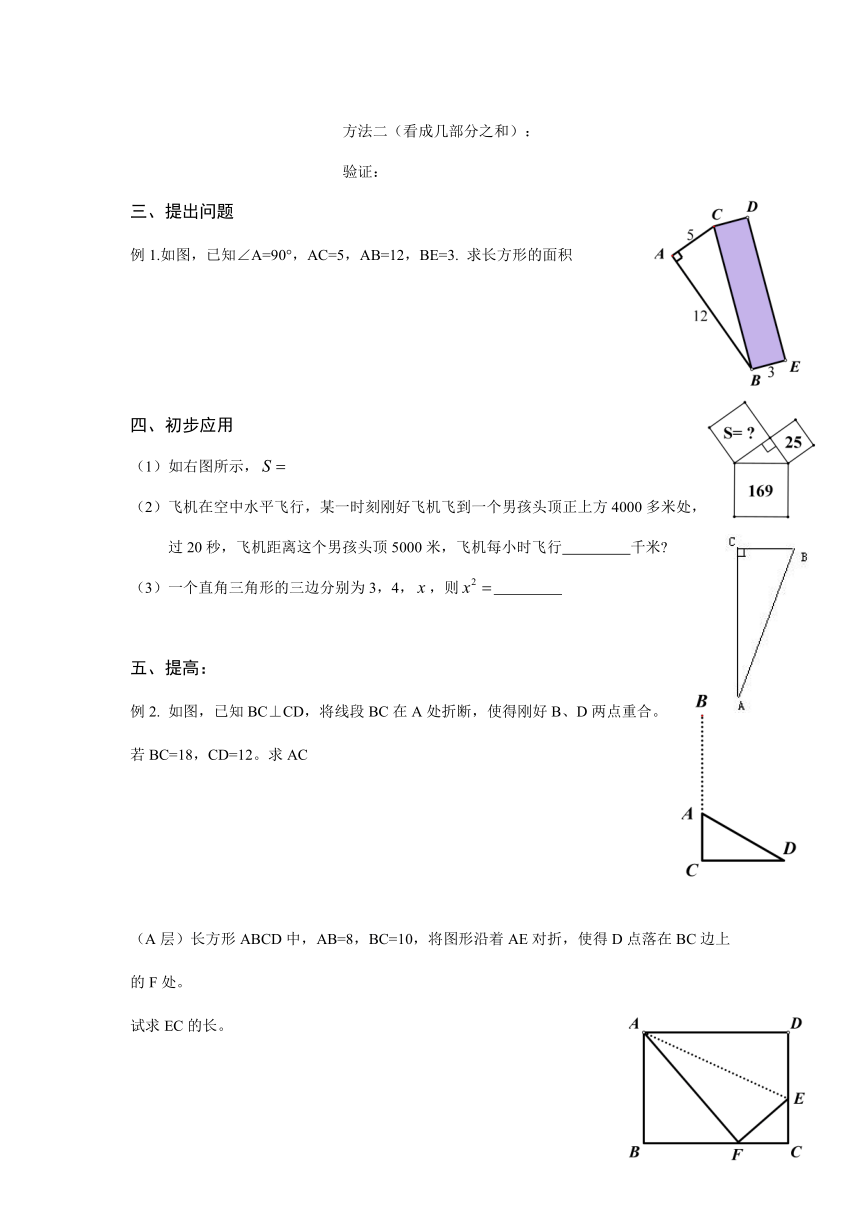
例1.如图，已知∠A=90°，AC=5，AB=12，BE=3. 求长方形的面积
四、初步应用
（1）如右图所示，
（2）飞机在空中水平飞行，某一时刻刚好飞机飞到一个男孩头顶正上方4000多米处，
过20秒，飞机距离这个男孩头顶5000米，飞机每小时飞行 千米
（3）一个直角三角形的三边分别为3，4，，则
五、提高：
例2. 如图，已知BC⊥CD，将线段BC在A处折断，使得刚好B、D两点重合。
若BC=18，CD=12。求AC
（A层）长方形ABCD中，AB=8，BC=10，将图形沿着AE对折，使得D点落在BC边上的F处。
试求EC的长。
六、小结：本节课你收获了什么 用自己的话整理下来
七、验收落实：
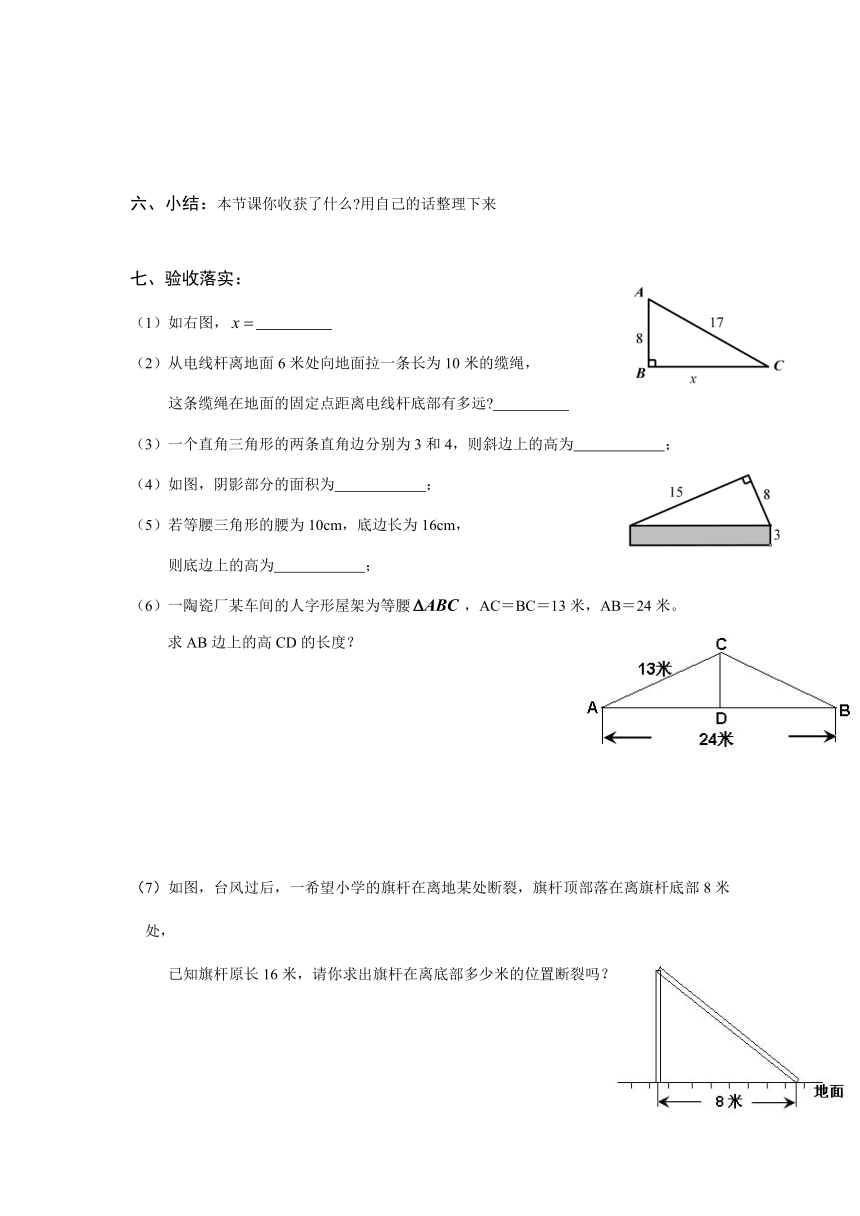
（1）如右图，
（2）从电线杆离地面6米处向地面拉一条长为10米的缆绳，
这条缆绳在地面的固定点距离电线杆底部有多远
（3）一个直角三角形的两条直角边分别为3和4，则斜边上的高为 ；
（4）如图，阴影部分的面积为 ；
（5）若等腰三角形的腰为10cm，底边长为16cm，
则底边上的高为 ；
（6）一陶瓷厂某车间的人字形屋架为等腰，AC＝BC＝13米，AB＝24米。
求AB边上的高CD的长度？
（7）如图，台风过后，一希望小学的旗杆在离地某处断裂，旗杆顶部落在离旗杆底部8米处，
已知旗杆原长16米，请你求出旗杆在离底部多少米的位置断裂吗？
答 案
一、回顾:
（1）直角三角形两直角边的平方之和等于斜边的平方
（2）
（3）在一个直角三角形中，两条直角边分别为，，斜边为：
如果，，则17，面积为60；
如果，，则三角形的周长为30，面积为30；
二、导学:（验证勾股定理）
（1）
方法一：
方法二：
（2） 方法一（公式法）：
方法二（看成几部分之和）：
验证：∴
∴
∴
三、提出问题
例1. 如图，已知∠A=90°，AC=5，AB=12，BE=3. 求长方形的面积
解：在Rt△ABC中，
∴ ∴BC=13
∴
四、初步应用
（1） （2）150 （3）25或7
五、提高：
例2. 已知BC⊥CD，将线段BC在A处折断，使得刚好B、D两点重合。
若BC=18，CD=12。求AC
解：设， ∴ ∴
∴ 在Rt△ACD中，由勾股定理可得：
∴ ，解得
∴ AC=5
长方形ABCD中，AB=8，BC=10，将图形沿着AE对折，使得D点落在BC边上的F处。
试求EC的长。
解：由折叠可知，AF=AD=AB=10，而AB=8
∴在Rt△ABF中，由勾股定理可得：
∴，解得，
∴ BF=6 ，∴CF=4
设， ∴ ∴
∴ 在Rt△CEF中，由勾股定理可得：
，解得
∴EC=5
七、验收落实：
（1） （2）8米 （3）2.4
（4）51 （5）6cm
（6）一陶瓷厂某车间的人字形屋架为等腰，AC＝BC＝13米，AB＝24米。
求AB边上的高CD的长度？
解：∵AB=BC 且CD是AB边上的高，
∴AD=AB=12米
∴在Rt△ACD中，由勾股定理可得：
∴，解得，
∴CD=5米
（7）如图，台风过后，一希望小学的旗杆在离地某处断裂，旗杆顶部落在离旗杆底部8米处，
已知旗杆原长16米，请你求出旗杆在离底部多少米的位置断裂吗？
解：设旗杆在离底部x米的位置断裂，
即AC=x米，则BC=米
∴在在Rt△ABC中，由勾股定理可得：
∴，解得
答：旗杆在离底部5米的位置断裂