六年级数学上册课件 第四单元比人教版(共27张PPT)
文档属性
| 名称 | 六年级数学上册课件 第四单元比人教版(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 13.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 16:19:04 | ||
图片预览






文档简介
(共27张PPT)
第1课时
比的意义
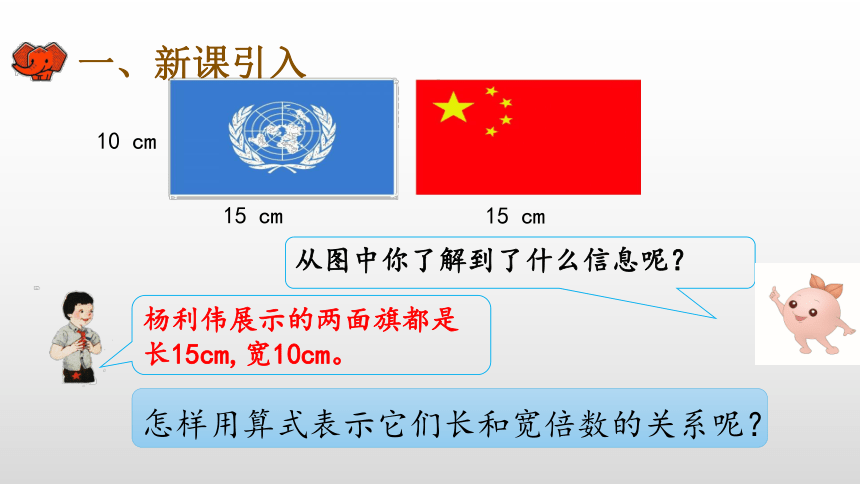
2003年10月15日,我国第一艘载人飞船“神舟”五号顺利升空。在太空中,执行此次任务的航天员杨利伟在飞船里向人们展示了联合国旗和中华人民共和国国旗。
一、新课引入
一、新课引入
杨利伟展示的两面旗都是长15cm,宽10cm。
怎样用算式表示它们长和宽倍数的关系呢?
从图中你了解到了什么信息呢?
15
cm
15
cm
10
cm
可以用“15÷10”表示长是宽的多少倍。
也可以用“10÷15”表示宽是长的几分之几。
有时我们也把这两个数量之间的关系说成:
长和宽的比是15比10,宽和长的比是10比15。
二、例题讲解
(一)同类量的比
(二)不同类量的比
“神舟”五号进入运行轨道后,在距地
350
km的高空做圆周运动,平均
90
分钟绕地球一周,大约运行
42252
km。
飞船进入轨道后平均每分钟飞行多少千米?用算式怎样表示?
二、例题讲解
我们也可以用比来表示路程和时间的关系:路程和时间的比是42252比90。
÷
速度可以用“路程
时间”表示。
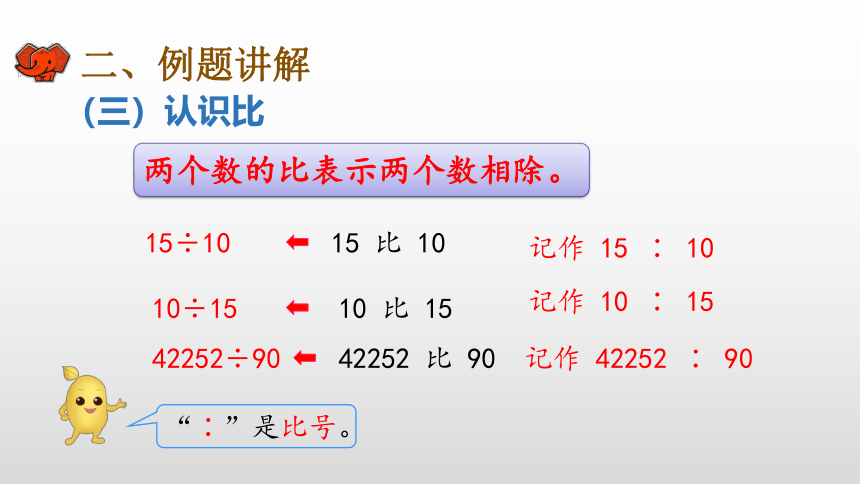
15÷10
15
比
10
10÷15
10
比
15
42252÷90
42252
比
90
记作
15
∶
10
记作
10
∶
15
记作
42252
∶
90
“∶”是比号。
二、例题讲解
(三)认识比
两个数的比表示两个数相除。
在两个数的比中,比号前面的数叫做比的前项,比号后面的数叫做比的后项。比的前项除以后项所得的商,叫做比值。例如:
比值通常用分数表示,也可以用小数或整数表示。
二、例题讲解
(三)认识比
15
∶
10
=
15
÷
10
=
……
前
项
……
比号
……
后项
……
比值
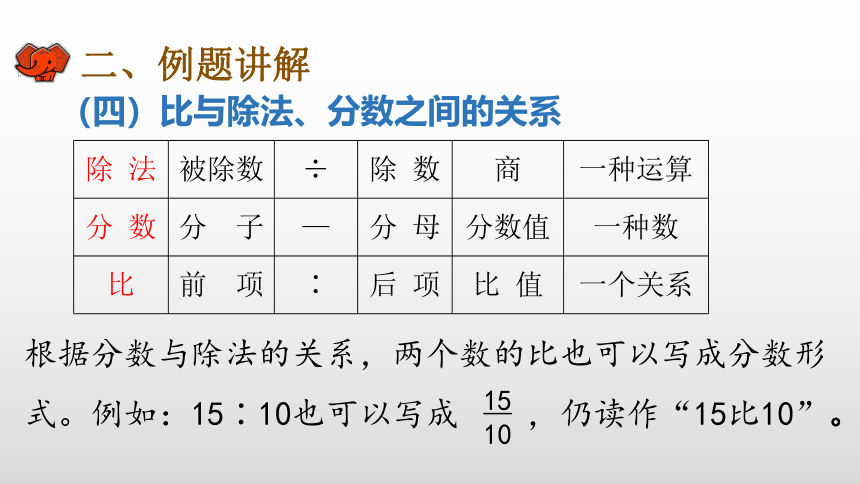
3
2
除
法
被除数
÷
除
数
商
一种运算
分
数
分
子
—
分
母
分数值
一种数
比
前
项
∶
后
项
比
值
一个关系
二、例题讲解
(四)比与除法、分数之间的关系
根据分数与除法的关系,两个数的比也可以写成分数形式。例如:15∶10也可以写成
,仍读作“15比10”。
15
10
二、例题讲解
(四)比与除法、分数之间的关系
因为比的后项相当于除法中的除数、分数中的分母,而除数和分母都不可以为0,所以比的后项也不能是0。
比的后项可以是0吗?
(1)小敏和小亮在文具店买同样的练习本。小敏买了6本,共花了1.8元。小亮买了8本,共花了2.4元。小敏和小亮买的练习本本数之比是(
)∶(
),比值是(
);花的钱数之比是
(
):(
),比值是(
)。
6
8
0.75
1.8
0.75
2.4
(2)
3∶(
)=
24
(
)∶8
=
0.5
1
8
4
三、新知运用
1.(教材P49做一做)认真填写。
4
8
0.9
0.3
=4÷8
=0.5
=0.9÷0.3
=3
=8÷2
=4
三、新知运用
2.说出下面每个比的前项和后项,并求出比值。
8
2
:
:
数的比是(
)∶(
),比值是(
)。女生与小组总人数的比是(
)∶(
),比值是(
)。
(3)汽车模型小组做的模型总数与人数的比是(
)∶(
),比值是
(
)。
14
10
16
8
10
26
18
12
三、新知运用
3.(教材P52第1题)
(1)航海模型小组男女生人数的比是(
)∶(
),比值是(
)。
(2)航空模型小组男女生人
回顾本节课的学习,你认为哪些内容很重要?你学会了吗?
四、课堂小结
1.两个数的比表示两个数相除。
2.在两个数的比中,比号前面的数叫做比的前项,比号后面的数叫做比的后项。比的前项除以后项所得的商,叫做比值。
3.比值通常用分数表示,也可以用小数或整数表示。
4.比的后项不能是0。
五、课后作业
完成课本“练习十一”第52页第2、3题。
第2课时
比的基本性质
谁折的速度快呢?
小明、小强、小丽都喜欢制作折纸。有一天,他们三人在争论谁每分钟折的纸鹤数多?
小明说:“我折的纸鹤数与时间(分)的比是6︰8。”
小强说:“我折的纸鹤数与时间(分)的比是3︰4。”
小丽说:“我折的纸鹤数与时间(分)的比是12︰16。”
一、新课引入
可以利用比和除法的关系来解决。
6︰8=6÷8=
=
3︰4=3÷4=
12︰16=12÷16=
=
6
8
3
4
3
4
12
16
3
4
一、新课引入
1.
这三个比有什么相同和不同之处?
2.
这三个比中有什么规律吗?这与除法中商不变的性质有什么联系呢?
先利用比和除法的关系来研究。
6∶8=6÷8=
=
6
8
3
4
12∶16=12÷16=
=
12
16
3
4
二、例题讲解
(一)探究比的基本性质
借助商不变的性质你发现比中有什么规律?
小结:比的前项和后项同时乘或除以相同的数(0除外),比值不变,这叫做比的基本性质。
6÷8
=(6×2)÷(8×2)=12÷16
6÷8
=(6÷2)÷(8÷2)=3÷4
6︰8
=(6×2)︰(8×2)
=12︰16
=(6÷2)︰(8÷2)
=3︰4
二、例题讲解
(一)探究比的基本性质
6︰8
(1)“神舟”五号搭载了两面联合国旗,一面长15cm,宽10cm(前面展示过),另一面长180cm,宽120cm(如图)。
1
15cm
10cm
180cm
120cm
二、例题讲解
(二)化简比
这两面联合国旗长和宽的最简单
的整数比分别是多少?
15∶10
=(15÷5)∶(10÷5)
=
3∶2
180∶120
=(180÷
)∶(120÷
)
=(
)∶(
)
想:5是15和10的什么数?为什么要除以5?
60
60
3
2
二、例题讲解
通过上面两个比的化简,你能说说化简整数比的方法吗?
根据比的基本性质,可以把比化简成最简单的整数比。
(2)把下面各比化成最简单的整数比
当一个比的前项和后项不是整数时,怎样把它化成最简单整数比?
0.75︰2
0.75︰2=(0.75×100)︰(2×100)
=75︰200
=(
)︰(
)
二、例题讲解
︰
1
6
2
9
2
9
2
9
1
6
×18
︰(
)=(
):(
)
1
6
︰
=(
)
×
18
为什么要乘18?
3
4
3
8
1.(教材P51做一做)把下面各比化成最简单的整数比。
32︰16
=2︰1
48︰40
=6︰5
0.15︰0.3
=1︰2
=5︰1
=14︰9
=1︰5
6
5
6
1
︰
8
3
︰
12
7
8
5
0.125︰
三、新知运用
2.判断正误。
(1)比的前项和后项同时乘或除一个相同的数,比值不变。
(
)
(2)10克盐溶解在100克水中,这时盐和盐水的比是1∶10。
(
)
×
×
三、新知运用
回顾本节课的学习,你认为哪些内容很重要?你学会了吗?
四、课堂小结
四、课堂小结
小数比的化简方法:
分数比的化简方法:
1.比的前项和后项同时乘它们分母的最小公倍数,转化成整数比,再进行化简。
2.利用求比值的方法也可以化简分数比,但结果必须写成比的形式。
先把比的前项和后项的小数点同时向右移动相同的位
数,转化成整数比,再按照整数比的化简方法进行化简。
五、课后作业
完成课本“练习十一”第53页第4题。
第1课时
比的意义
2003年10月15日,我国第一艘载人飞船“神舟”五号顺利升空。在太空中,执行此次任务的航天员杨利伟在飞船里向人们展示了联合国旗和中华人民共和国国旗。
一、新课引入
一、新课引入
杨利伟展示的两面旗都是长15cm,宽10cm。
怎样用算式表示它们长和宽倍数的关系呢?
从图中你了解到了什么信息呢?
15
cm
15
cm
10
cm
可以用“15÷10”表示长是宽的多少倍。
也可以用“10÷15”表示宽是长的几分之几。
有时我们也把这两个数量之间的关系说成:
长和宽的比是15比10,宽和长的比是10比15。
二、例题讲解
(一)同类量的比
(二)不同类量的比
“神舟”五号进入运行轨道后,在距地
350
km的高空做圆周运动,平均
90
分钟绕地球一周,大约运行
42252
km。
飞船进入轨道后平均每分钟飞行多少千米?用算式怎样表示?
二、例题讲解
我们也可以用比来表示路程和时间的关系:路程和时间的比是42252比90。
÷
速度可以用“路程
时间”表示。
15÷10
15
比
10
10÷15
10
比
15
42252÷90
42252
比
90
记作
15
∶
10
记作
10
∶
15
记作
42252
∶
90
“∶”是比号。
二、例题讲解
(三)认识比
两个数的比表示两个数相除。
在两个数的比中,比号前面的数叫做比的前项,比号后面的数叫做比的后项。比的前项除以后项所得的商,叫做比值。例如:
比值通常用分数表示,也可以用小数或整数表示。
二、例题讲解
(三)认识比
15
∶
10
=
15
÷
10
=
……
前
项
……
比号
……
后项
……
比值
3
2
除
法
被除数
÷
除
数
商
一种运算
分
数
分
子
—
分
母
分数值
一种数
比
前
项
∶
后
项
比
值
一个关系
二、例题讲解
(四)比与除法、分数之间的关系
根据分数与除法的关系,两个数的比也可以写成分数形式。例如:15∶10也可以写成
,仍读作“15比10”。
15
10
二、例题讲解
(四)比与除法、分数之间的关系
因为比的后项相当于除法中的除数、分数中的分母,而除数和分母都不可以为0,所以比的后项也不能是0。
比的后项可以是0吗?
(1)小敏和小亮在文具店买同样的练习本。小敏买了6本,共花了1.8元。小亮买了8本,共花了2.4元。小敏和小亮买的练习本本数之比是(
)∶(
),比值是(
);花的钱数之比是
(
):(
),比值是(
)。
6
8
0.75
1.8
0.75
2.4
(2)
3∶(
)=
24
(
)∶8
=
0.5
1
8
4
三、新知运用
1.(教材P49做一做)认真填写。
4
8
0.9
0.3
=4÷8
=0.5
=0.9÷0.3
=3
=8÷2
=4
三、新知运用
2.说出下面每个比的前项和后项,并求出比值。
8
2
:
:
数的比是(
)∶(
),比值是(
)。女生与小组总人数的比是(
)∶(
),比值是(
)。
(3)汽车模型小组做的模型总数与人数的比是(
)∶(
),比值是
(
)。
14
10
16
8
10
26
18
12
三、新知运用
3.(教材P52第1题)
(1)航海模型小组男女生人数的比是(
)∶(
),比值是(
)。
(2)航空模型小组男女生人
回顾本节课的学习,你认为哪些内容很重要?你学会了吗?
四、课堂小结
1.两个数的比表示两个数相除。
2.在两个数的比中,比号前面的数叫做比的前项,比号后面的数叫做比的后项。比的前项除以后项所得的商,叫做比值。
3.比值通常用分数表示,也可以用小数或整数表示。
4.比的后项不能是0。
五、课后作业
完成课本“练习十一”第52页第2、3题。
第2课时
比的基本性质
谁折的速度快呢?
小明、小强、小丽都喜欢制作折纸。有一天,他们三人在争论谁每分钟折的纸鹤数多?
小明说:“我折的纸鹤数与时间(分)的比是6︰8。”
小强说:“我折的纸鹤数与时间(分)的比是3︰4。”
小丽说:“我折的纸鹤数与时间(分)的比是12︰16。”
一、新课引入
可以利用比和除法的关系来解决。
6︰8=6÷8=
=
3︰4=3÷4=
12︰16=12÷16=
=
6
8
3
4
3
4
12
16
3
4
一、新课引入
1.
这三个比有什么相同和不同之处?
2.
这三个比中有什么规律吗?这与除法中商不变的性质有什么联系呢?
先利用比和除法的关系来研究。
6∶8=6÷8=
=
6
8
3
4
12∶16=12÷16=
=
12
16
3
4
二、例题讲解
(一)探究比的基本性质
借助商不变的性质你发现比中有什么规律?
小结:比的前项和后项同时乘或除以相同的数(0除外),比值不变,这叫做比的基本性质。
6÷8
=(6×2)÷(8×2)=12÷16
6÷8
=(6÷2)÷(8÷2)=3÷4
6︰8
=(6×2)︰(8×2)
=12︰16
=(6÷2)︰(8÷2)
=3︰4
二、例题讲解
(一)探究比的基本性质
6︰8
(1)“神舟”五号搭载了两面联合国旗,一面长15cm,宽10cm(前面展示过),另一面长180cm,宽120cm(如图)。
1
15cm
10cm
180cm
120cm
二、例题讲解
(二)化简比
这两面联合国旗长和宽的最简单
的整数比分别是多少?
15∶10
=(15÷5)∶(10÷5)
=
3∶2
180∶120
=(180÷
)∶(120÷
)
=(
)∶(
)
想:5是15和10的什么数?为什么要除以5?
60
60
3
2
二、例题讲解
通过上面两个比的化简,你能说说化简整数比的方法吗?
根据比的基本性质,可以把比化简成最简单的整数比。
(2)把下面各比化成最简单的整数比
当一个比的前项和后项不是整数时,怎样把它化成最简单整数比?
0.75︰2
0.75︰2=(0.75×100)︰(2×100)
=75︰200
=(
)︰(
)
二、例题讲解
︰
1
6
2
9
2
9
2
9
1
6
×18
︰(
)=(
):(
)
1
6
︰
=(
)
×
18
为什么要乘18?
3
4
3
8
1.(教材P51做一做)把下面各比化成最简单的整数比。
32︰16
=2︰1
48︰40
=6︰5
0.15︰0.3
=1︰2
=5︰1
=14︰9
=1︰5
6
5
6
1
︰
8
3
︰
12
7
8
5
0.125︰
三、新知运用
2.判断正误。
(1)比的前项和后项同时乘或除一个相同的数,比值不变。
(
)
(2)10克盐溶解在100克水中,这时盐和盐水的比是1∶10。
(
)
×
×
三、新知运用
回顾本节课的学习,你认为哪些内容很重要?你学会了吗?
四、课堂小结
四、课堂小结
小数比的化简方法:
分数比的化简方法:
1.比的前项和后项同时乘它们分母的最小公倍数,转化成整数比,再进行化简。
2.利用求比值的方法也可以化简分数比,但结果必须写成比的形式。
先把比的前项和后项的小数点同时向右移动相同的位
数,转化成整数比,再按照整数比的化简方法进行化简。
五、课后作业
完成课本“练习十一”第53页第4题。
