2021-2022学年高一下学期数学人教B版(2019)必修第四册第九章《解三角形》本章小结(21张PPT)
文档属性
| 名称 | 2021-2022学年高一下学期数学人教B版(2019)必修第四册第九章《解三角形》本章小结(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 585.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 17:21:03 | ||
图片预览







文档简介
(共21张PPT)
《解三角形》
本章小结
人教版普通高中数学B版必修第四册
第一章
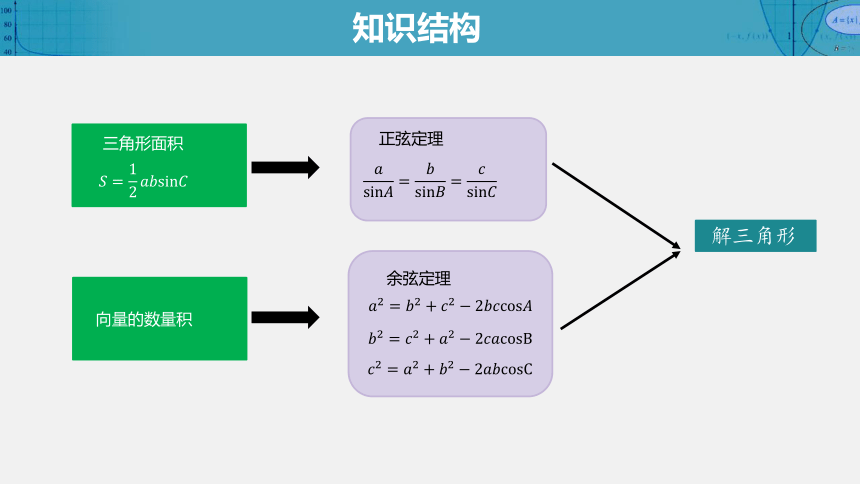
三角形面积
向量的数量积
正弦定理
余弦定理
解三角形
知识结构
知识结构--方法点睛
(2)根据题意画出示意图,将实际问题抽象成解三角形问题;
(3)选择正弦定理或余弦定理求解;
知识结构--方法点睛
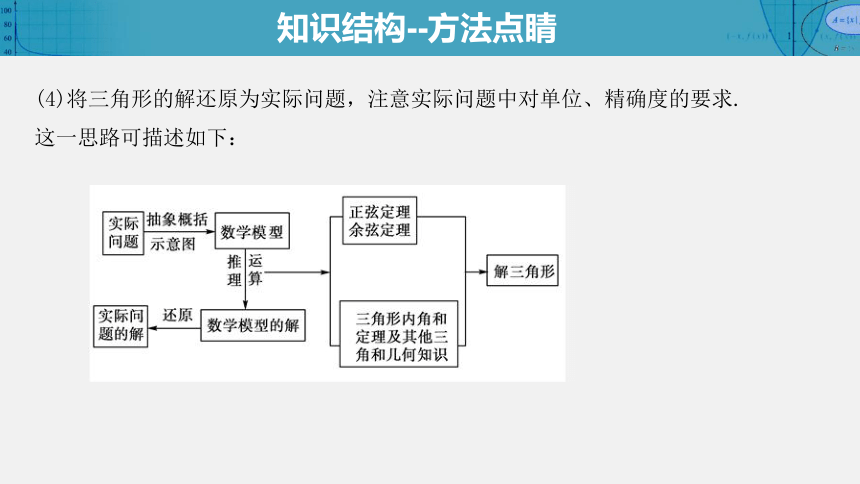
(4)将三角形的解还原为实际问题,注意实际问题中对单位、精确度的要求.这一思路可描述如下:
知识结构--方法点睛
1.每小组同学分工合作,利用网络或书籍查找已有的测角仪,并将手机的资料整理成演讲材料,并与其他同学交流。
2.尝试自己制作合适的测角仪
小秘密:如果是别人没有想到过的点子,可以申请专利哦
课题作业
题型一 应用正、余弦定理解三角形
这类问题一般要先审查题设条件,进行归类,根据题目类型确定应用哪个定理入手解决.
随堂练习
题型一 应用正、余弦定理解三角形
必修四教材19页A组1题
解:
随堂练习
题型一 应用正、余弦定理解三角形
必修四教材19页A组2题
解:
随堂练习
练习:在△ABC中,由已知条件解三角形,其中有两解的是( )
A.b=20,A=45°,C=80°
B.a=30,c=28,B=60°
C.a=14,b=16,A=45°
D.a=12,c=15,A=120°
随堂练习
[答案] C
随堂练习
题型二 判断三角形的形状
根据所给条件确定三角形的形状,主要有两条途径:(1)化边为角;(2)化角为边.
常见具体方法有:
①通过正弦定理实施边角转换;
②通过余弦定理实施边角转换;
③通过三角变换找出角之间的关系;
④通过三角函数值符号的判断及正、余弦函数有界性的讨论;另外要注意b2+c2-a2>0?A为锐角,b2+c2-a2=0?A为直角,b2+c2-a2<0?A为钝角.
随堂练习
题型二 判断三角形的形状
必修四教材19页A组4题
随堂练习
答案:
(2),(3),(4)
必修四教材20页B组1题
随堂练习
题型三 解三角形的应用题
解三角形应用题常见的几种情况:
(1)实际问题经抽象概括后,已知量与未知量全部集中在一个三角形中,可用正弦定理或余弦定理求解.
(2)实际问题经抽象概括后,已知量与未知量涉及到两个(或两个以上)三角形,这时需作出这些三角形,先解够条件的三角形,然后逐步求出其它三角形中的解,有时需设出未知量,从几个三角形中列出方程,解方程得出所要求的解.
常见题型有:测量距离问题、测量高度问题、测量角度问题、计算面积问题等.
随堂练习
题型三 解三角形的应用题
随堂练习
随堂练习
随堂练习
随堂练习
课堂小结
1.本章知识结构图
2.总结正弦定理、余弦定理的应用类型以及方法点睛
3.渗透数学抽象、数学运算和数学建模的学科素养.
谢
谢
看
观
谢
谢
看
观
谢
谢
看
观
《解三角形》
本章小结
人教版普通高中数学B版必修第四册
第一章
三角形面积
向量的数量积
正弦定理
余弦定理
解三角形
知识结构
知识结构--方法点睛
(2)根据题意画出示意图,将实际问题抽象成解三角形问题;
(3)选择正弦定理或余弦定理求解;
知识结构--方法点睛
(4)将三角形的解还原为实际问题,注意实际问题中对单位、精确度的要求.这一思路可描述如下:
知识结构--方法点睛
1.每小组同学分工合作,利用网络或书籍查找已有的测角仪,并将手机的资料整理成演讲材料,并与其他同学交流。
2.尝试自己制作合适的测角仪
小秘密:如果是别人没有想到过的点子,可以申请专利哦
课题作业
题型一 应用正、余弦定理解三角形
这类问题一般要先审查题设条件,进行归类,根据题目类型确定应用哪个定理入手解决.
随堂练习
题型一 应用正、余弦定理解三角形
必修四教材19页A组1题
解:
随堂练习
题型一 应用正、余弦定理解三角形
必修四教材19页A组2题
解:
随堂练习
练习:在△ABC中,由已知条件解三角形,其中有两解的是( )
A.b=20,A=45°,C=80°
B.a=30,c=28,B=60°
C.a=14,b=16,A=45°
D.a=12,c=15,A=120°
随堂练习
[答案] C
随堂练习
题型二 判断三角形的形状
根据所给条件确定三角形的形状,主要有两条途径:(1)化边为角;(2)化角为边.
常见具体方法有:
①通过正弦定理实施边角转换;
②通过余弦定理实施边角转换;
③通过三角变换找出角之间的关系;
④通过三角函数值符号的判断及正、余弦函数有界性的讨论;另外要注意b2+c2-a2>0?A为锐角,b2+c2-a2=0?A为直角,b2+c2-a2<0?A为钝角.
随堂练习
题型二 判断三角形的形状
必修四教材19页A组4题
随堂练习
答案:
(2),(3),(4)
必修四教材20页B组1题
随堂练习
题型三 解三角形的应用题
解三角形应用题常见的几种情况:
(1)实际问题经抽象概括后,已知量与未知量全部集中在一个三角形中,可用正弦定理或余弦定理求解.
(2)实际问题经抽象概括后,已知量与未知量涉及到两个(或两个以上)三角形,这时需作出这些三角形,先解够条件的三角形,然后逐步求出其它三角形中的解,有时需设出未知量,从几个三角形中列出方程,解方程得出所要求的解.
常见题型有:测量距离问题、测量高度问题、测量角度问题、计算面积问题等.
随堂练习
题型三 解三角形的应用题
随堂练习
随堂练习
随堂练习
随堂练习
课堂小结
1.本章知识结构图
2.总结正弦定理、余弦定理的应用类型以及方法点睛
3.渗透数学抽象、数学运算和数学建模的学科素养.
谢
谢
看
观
谢
谢
看
观
谢
谢
看
观
