7.2 离散型随机变量及其分布列 讲义-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(Word含答案)
文档属性
| 名称 | 7.2 离散型随机变量及其分布列 讲义-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(Word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 328.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 17:24:42 | ||
图片预览




文档简介
第七章 随机变量及其分布
第七章 随机变量及其分布
7.2离散型随机变量及其分布列
7.2离散型随机变量及其分布列
知识梳理
知识梳理
知识点一 随机变量的概念、表示及特征
概念:一般地,对于随机试验样本空间Ω中的每个样本点ω都有唯一的实数X(ω)与之对应,我们称X为随机变量.
表示:用大写英文字母表示随机变量,如X,Y,Z;用小写英文字母表示随机变量的取值,如x,y,z.
特征:随机试验中,每个样本点都有唯一的一个实数与之对应,随机变量有如下特征:
(1)取值依赖于样本点.
(2)所有可能取值是明确的.
知识点二 随机变量与函数有什么联系和区别?
共同点:随机变量和函数都是一种映射
区别: 随机变量把试验的结果映为实数,函数把实数映为实数
联系:试验结果的范围相当于函数的定义域,随机变量的取值范围相当与函数的值域;
注意:所有随机变量的取值范围的集合叫做随机变量的值域.
知识点三随机变量的分类:
1)离散型随机变量:
对于随机变量可能取的值,如果可以一一列出,这样的随机变量叫做离散型随机变量.
2)连续型随机变量:
随机变量可以取某一区间内的一切值,这样的随机变量叫做连续型随机变量.
知识点四离散型随机变量的分布列及其性质
1.定义:一般地,设离散型随机变量X的可能取值为x1,x2,…,xn,我们称X取每一个值xi的概率P(X=xi)=pi,i=1,2,3,…,n为X的概率分布列,简称分布列.
2.分布列的性质
(1)pi≥0,i=1,2,…,n.
(2)p1+p2+…+pn=1.
题型探究
题型探究
例1.学校趣味运动会上增加了一项射击比赛,比赛规则如下:向A、B两个靶子进行射击,先向A靶射击一次,命中得1分,没有命中得0分;再向B靶连续射击两次,如果只命中一次得2分,一次也没有命中得0分,如果连续命中两次则得5分.甲同学准备参赛,经过一定的训练,甲同学的射击水平显著提高,目前的水平是:向A靶射击,命中的概率是false;向B靶射击,命中的概率为false.假设甲同学每次射击结果相互独立.
(1)求甲同学恰好命中一次的概率;
(2)求甲同学获得的总分X的分布列及数学期望.
【答案】(1)false;(2)分布列见解析;期望为false.
【详解】
(1)记“甲同学恰好命中一次”为事件C,“甲射击命中A靶”为事件D,
“甲第一次射击B靶命中”为事件E,“甲第二次射击B靶命中”为事件F,由题意可知false,false.
由于false,
false.
(2)随机变量X的可能取值为:0,1,2,3,5,6.
false
false
false
false
false
false
X
0
1
2
3
5
6
P
false
false
false
false
false
false
false.
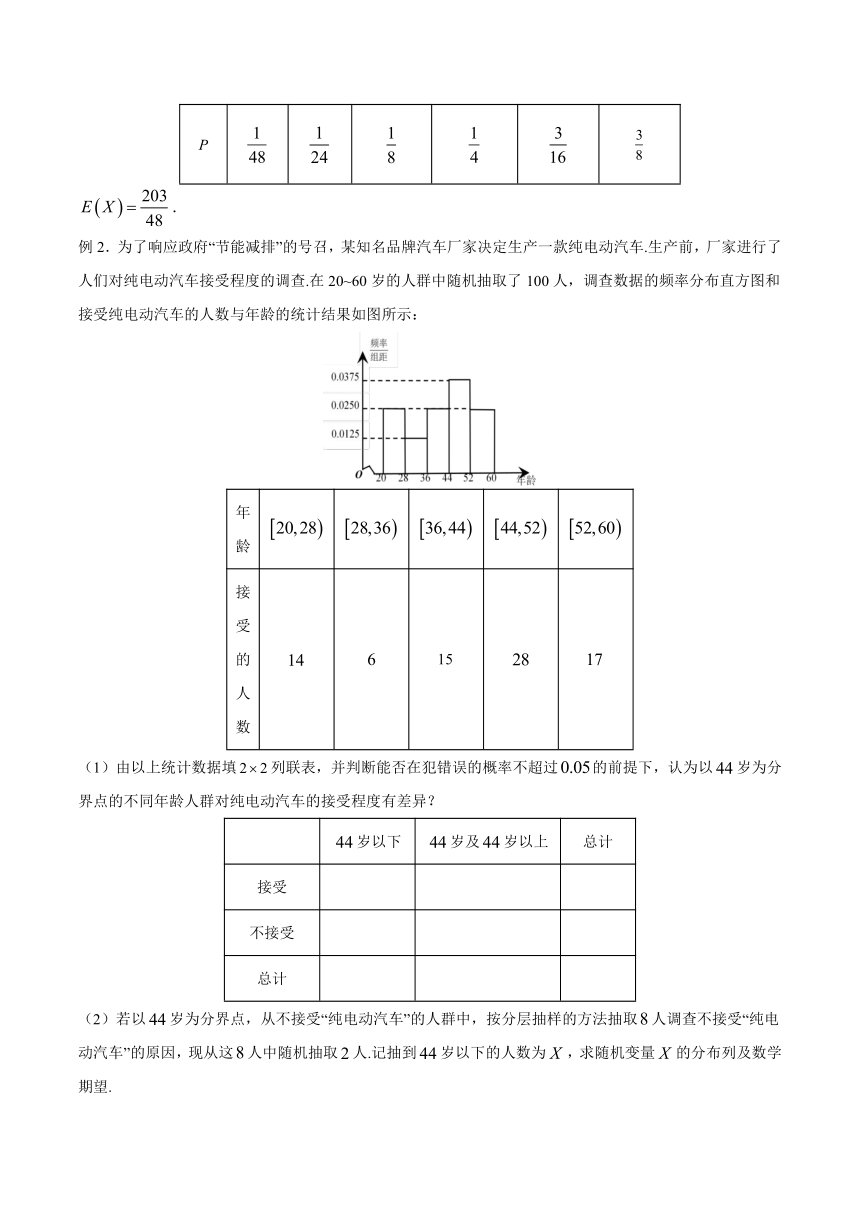
例2.为了响应政府“节能减排”的号召,某知名品牌汽车厂家决定生产一款纯电动汽车.生产前,厂家进行了人们对纯电动汽车接受程度的调查.在20~60岁的人群中随机抽取了100人,调查数据的频率分布直方图和接受纯电动汽车的人数与年龄的统计结果如图所示:
年龄
false
false
false
false
false
接受的人数
false
false
false
false
false
(1)由以上统计数据填false列联表,并判断能否在犯错误的概率不超过false的前提下,认为以false岁为分界点的不同年龄人群对纯电动汽车的接受程度有差异?
false岁以下
false岁及false岁以上
总计
接受
不接受
总计
(2)若以false岁为分界点,从不接受“纯电动汽车”的人群中,按分层抽样的方法抽取false人调查不接受“纯电动汽车”的原因,现从这false人中随机抽取false人.记抽到false岁以下的人数为false,求随机变量false的分布列及数学期望.
false
0.100
0.050
0.010
0.001
false
2.706
3.841
6.635
10.828
附:
false
【答案】(1)联表答案见解析,能在犯错误的概率不超过false的前提下,认为以false岁为分界点的不同人群对“纯电动汽车”的接受程度有差异;(2)分布列答案见解析,数学期望为false.
【详解】
解:(1)由题可得false联表如下:
false岁以下
false岁及false岁以上
总计
接受
35
45
80
不接受
15
5
20
总计
50
50
100
∵false.
∴能在犯错误的概率不超过false的前提下,认为以false岁为分界点的不同人群对“纯电动汽车”的接受程度有差异.
(2)由题意可知,抽取的false人中false岁以下的有false人,false岁及false岁以上的有false人,所以false的可能取值有false,false,false.
falsefalsefalse
所以随机变量false的分布列为:
false
false
false
false
false
false
false
false
false.
例3.某单位招考工作人员,须参加初试和复试,初试通过后组织考生参加复试,共5000人参加复试,复试共三道题,第一题考生答对得3分,答错得0分,后两题考生每答对一道题得5分,答错得0分,答完三道题后的得分之和为考生的复试成绩.
(1)通过分析可以认为考生初试成绩false服从正态分布false,其中false,false,试估计初试成绩不低于90分的人数;
(2)已知某考生已通过初试,他在复试中第一题答对的概率为false,后两题答对的概率均为false,且每道题回答正确与否互不影响.记该考生的复试试成绩为false,求false的分布列及数学期望.
附:若随机变量false服从正态分布false,则false,false,false.
【答案】(1)114人;(2)分布列见解析,false.
【详解】
(1)∵学生笔试成绩false服从正态分布false,其中false,false,
false
∴false
∴估计笔试成绩不低于90分的人数为false人
(2)false的取值分别为0,3,5,8,10,13,
则false
false
false
false
false
false
false的分布为
故false的分布列为:
false
0
3
5
8
10
13
false
false
false
false
false
false
false
false
例4.某篮球职业联赛分为常规赛和季后赛两个阶段.常规赛采用循环赛,分主场比赛和客场比赛两种,积分高的球队进入季后赛;季后赛采用五局三胜制进行淘汰赛,最终决出总冠军.(“false局false胜”制是指先胜false局者获得比赛胜利,比赛结束).下表是甲队在常规赛false场比赛中的比赛结果记录表.
季度
比赛次数
主场次数
获胜次数
主场获胜次数
1季度
23
13
16
11
2季度
27
11
21
8
3季度
30
16
23
13
(1)根据表中信息,能否在犯错误概率不超过false的前提下认为“主客场”与“胜负”之间有关?
(2)已知甲队和乙队在季后赛首轮比赛中相遇,假设每局比赛结果相互独立,以甲队常规赛false场比赛获胜的频率估计甲队在季后赛每局比赛获胜的概率,记false为本轮比赛结束时甲队和乙队所进行的比赛的局数,求false的分布列及甲队获得这轮比赛胜利的概率.
附:false,
P(K2≥k)
0.100
0.050
0.025
k
2.706
3.841
5.024
【答案】(1)不能在犯错误概率不超过false的前提下认为“主客场”与“比赛胜负”之间有关;(2)分布列答案见解析,概率为false.
【详解】
解:(1)根据表格信息列出2×2列联表如下
甲队胜
甲队负
合计
主场
32
8
40
客场
28
12
40
合计
60
20
80
false
所以不能在犯错误概率不超过0.100的前提下认为“主客场”与“比赛胜负”之间有关.
(2)依题意得甲队每局比赛获胜的概率估计值为false,
X的所有可能取值为false,false,false,
false
false
false
所以X的分布列为
X
3
4
5
P
false
false
false
“甲队获得这轮比赛胜利”的概率为false.
例5.抖音是一款音乐创意短视频社交软件,是一个专注年轻人的15秒音乐短视频社区,用户可以通过这款软件选择歌曲,拍摄15秒的音乐短视频,形成自己的作品.2018年6月首批25家央企集体入驻抖音,一调研员在某单位进行刷抖音时间的调查,若该单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人.
(1)应从甲、乙、丙三个部门的员工中分别抽取多少人?
(2)若抽出的7人中有3人是抖音迷,4人为非抖音迷,现从这7人中随机抽取3人做进一步的详细登记.
①用false表示抽取的3人中是抖音迷的员工人数,求随机变量false的分布列与数学期望;
②设false为事件“抽取的3人中,既有是抖音迷的员工,也有非抖音迷的员工’’,求事件false发生的概率.
【答案】(1)应从甲、乙、丙三个部门的员工中分别抽取3人,2人,2人;(2)①分布列详见解析,数学期望为false;(3)false.
【详解】
(1)由已知,甲、乙、丙三个部门的员工人数之比为false由于采用分层抽样的方法从中抽取7人,因此应从甲、乙、丙三个部门的员工中分别抽取3人,2人,2人.
(2)①随机变量X的所有可能取值为0,1,2,3.
false.
false,
false,
false,
false,
所以,随机变量false的分布列为
false
0
1
2
3
false
false
false
false
false
随机变量X的数学期望false.
②设事件false为“抽取的3人中,是抖音迷的员工有1人,非抖音迷的员工有2人”;事件false为“抽取的3人中,是抖音迷的员工有2人,非抖音迷的员工有1人”,则false,且false与false互斥,由(Ⅰ)知false,
false,
故false,
所以事件false发生的概率为false.
课后小练
课后小练
1.甲、乙是两名射击运动员,根据历史统计数据,甲一次射击命中 10 、 9 、 8 环的概率分别为 25 、 25 、 15 ,乙一次射击命中 10 、 9 环的概率分别为 16 、 56 .一轮射击中,甲、乙各射击一次.甲、乙射击相互独立,每次射击也互不影响.
(1)在一轮射击中,求甲命中的环数不高于乙命中的环数的概率;
(2)记一轮射击中,甲、乙命中的环数之和为 X ,求 X 的分布列;
(3)进行三轮射击,求甲、乙命中的环数之和不低于52环的概率.
2.受新冠肺炎疫情影响,本学期同学们在家上网课时间达三个多月,电脑屏幕代替了黑板,对同学们的视力造成了很大的损伤.某学校为了了解同学们现阶段的视力情况,对全校高三1000名学生的视力情况进行了调查,从中随机抽取了100名学生的体检表,绘制了频率分布直方图如图:
(1)求a的值,并估计这1000名学生视力的中位数(精确到0.01);
(2)为了进一步了解视力与学生成绩是否有关,对本年级名次在前50名与后50名的学生进行了调查,得到如下数据:
前50名
后50名
近视
42
32
不近视
8
18
根据表中数据,能否有95%把握认为视力与学习成绩有关?
(3)若报考某高校某专业的资格为:视力不低于5.0,以该样本数据来估计全市高三学生的视力,现从全市视力在4.8以上的同学中随机抽取4名同学,这4名同学中有资格报该校该专业的人数为 X ,求 X 的分布列及数学期望.
P(K2≥k)
0.10
0.05
0.025
0.010
0.005
k
2.706
3.841
5.024
6.635
7.879
3.2020年年初,新冠肺炎疫情防控工作全面有序展开.某社区对居民疫情防控知识进行了网上调研,调研成绩全部都在40分到100分之间.现从中随机选取200位居民的调研成绩进行统计,绘制了如图所示的频率分布直方图.
(1)求a的值,并估计这200位居民调研成绩的中位数;
(2)在成绩为 [40,50] , (90,100] 的两组居民中,用分层抽样的方法抽取6位居民,再从6位居民中随机抽取2位进行详谈.记X为2位居民的调研成绩在 [40,50] 的人数,求随机变量X的分布列.
4.为了了解学生的身体素质情况,现从某校学生中随机抽取10人进行体能测试,测试的分数(百分制)如茎叶图所示,根据有关国家标准成绩不低于79分的为优秀,将频率视为概率.
(1)另从我校学生中任取3人进行测试,求至少有1人成绩是“优秀”的概率;
(Ⅱ)从抽取的这10人(成绩见茎叶图)中随机选取3人,记X表示测试成绩为“优秀”的学生人数,求X的分布列和数学期望.
5.某单位组织“学习强国”知识竞赛,选手从6道备选题中随机抽取3道题.规定至少答对其中的2道题才能晋级.甲选手只能答对其中的4道题。
(1)求甲选手能晋级的概率;
(2)若乙选手每题能答对的概率都是 34 ,且每题答对与否互不影响,用数学期望分析比较甲、乙两选手的答题水平。
答案解析
1.【答案】 (1)解:设一次射击后,甲命中的环数为 ξ ,乙命中的环数为 η ,
则甲命中的环数不高于乙命中的环数为 P(ξ≤η)=P(ξ=8)+P(ξ=9)+P(ξ=10)P(η=10)=15+25+25×16=23 ;
(2)解:题意可知随机变量 X 的可能取值有 17 、 18 、 19 、 20 ,
P(X=17)=15×56=16 , P(X=18)=15×16+25×56=1130 ,
P(X=19)=25×16+25×56=25 , P(X=20)=25×16=115 ,
所以,随机变量 X 的分布列如下表所示:
X
17
18
19
20
P
16
1130
25
115
(3)解:每轮射击后,甲、乙命中的环数之和为17的概率为 p=15×56=16 ,
三轮射击后,甲、乙命中的环数之和最小为 17×3=51 ,
因此,进行三轮射击,求甲、乙命中的环数之和不低于52环的概率为 1?(16)3=215216 .
【解析】(1)设一次射击后,甲命中的环数为 ξ ,乙命中的环数为 η ,由题意可得 P(ξ≤η)=P(ξ=8)+P(ξ=9)+P(ξ=10)P(η=10) ,结合独立事件的概率乘法公式与互斥事件的概率公式可求得所求事件的概率;(2)由题意可知随机变量 X 的可能取值有17、18、19、20,利用独立事件的概率乘法公式可计算得出随机变量 X 在不同取值下的概率,可得出随机变量 X 的分布列;(3)求出每轮射击后,甲、乙命中的环数之和为17的概率,再利用独立事件的概率乘法公式以及对立事件的概率公式可求得所求事件的概率.
2.【答案】 (1)解: (0.25+0.5+2a+1+1.75)×0.2=1 ,所以 a=0.75 ,
视力在4.4以下的频率为: (0.5+0.75)×0.2=0.25 ,
视力在4.6以下的频率为: (0.5+0.75+1.75)×0.2=0.6 ,
所以中位数在4.4至4.6之间,设中位数为 x ,
则 (x?4.4)×1.75=0.5?0.25 , x≈4.54 ,故中位数为4.54.
(2)解:因为 K2 的观测值 k=100(42×18?8×32)250×50×74×26=2500481≈5.2>3.841 ,
所以有95%把握认为视力与学习成绩有关.
(3)解:视力在4.8以上的同学中,视力在5.0以上的同学所占的比例为: 0.250.25+0.75=14
所以从全市视力在4.8以上的同学中随机抽取4名同学,这4名同学中有资格报该校该专业的人数为 X~B(4,14) ,即 P(X=k)=C4k(14)k(34)4?k , k=0,1,2,3,4 ,
所以 P(X=0)=(34)4=81256 ,
P(X=1)=C41×14×(34)3=108256=2764 , P(X=2)=C42×(14)2×(34)2=54256=27128 ,
P(X=3)=C43×(14)3×34=12256=364 , P(X=4)=(14)4=1256 ,
所以 X 的分布列为:
X
0
1
2
3
4
P
81256
2764
27128
364
1256
E(X)=4×14=1 .
【解析】
(1)根据题意由频率分布直方图的性质能求出a和中位数.
(2)首先求出X2≈5.2>3.841,从而有95%把握认为视力与学习成绩有关.
(3)根据题意即可得出视力在4.8以上的同学中,视力在5.0以上的同学所占有比例为14 从全市视力在4.8以上的同学中随机抽取4名同学,这4名同学中有资格报该校专业的人数X~B(4,14) 由此能求出X的分布列和E(X).
3.【答案】 (1)解: (0.005+0.015+0.02+0.025×2+a)×10=1 ,
得 a=0.01 .
前3组的频率之和为 (0.005+0.015+0.02)×10=0.4 ,
第4组的频率为 0.025×10=0.25 ,
因为 0.4+0.25=0.65>0.5 ,所以中位数在第 4 组.
设中位数为 x ,则 (x?70)×0.025=0.1 ,解得 x=74 .
所以200位居民调研成绩的中位数为74分.
(2)解:成绩在 [40,50] , (90,100] 的居民人数分别为10人,20人,
所以在 [40,50] 的居民中应抽取 630×10=2 (人),
在 (90,100] 的居民中应抽取 630×20=4 (人).
X的可能取值为 0 , 1 , 2 ,
P(X=0)=C42C62=25 ,
P(X=1)=C41C21C62=815 ,
P(X=2)=C22C62=115 ,
所以X的分布列为:
X
0
1
2
P
25
815
115
【解析】(1)根据频率之和为1,由此算出a的值,利用频率分布直方图求中位数的方法设中位数为x,列式计算即可得出结论;(2)可知成绩在 [40,50] , (90,100] 的居民人数分别为10人,20人,根据分层抽样,可知抽取的6位中,成绩在 [40,50] 的人数为2人,成绩在 (90,100] 的人数为4人,则x的可能取值为0,1,2,求出相应概率,列出相应的分布列
4.【答案】 (1)解:(1)由茎叶图知,抽取的10人中成绩是“优秀”的有6人,频率为 35 ,依题意,从我校学生中任选1人,成绩是“优秀”的概率为 35 ,记事件 A 表示“在我校学生中任选3人,至少1人成绩是优良”,则 P(A)=1?C33(1?35)3=117125
(Ⅱ)由题意可得, X 的取值可能为0,1,2,3
P(X=0)=C43C103=130 ,
P(X=1)=C42C61C103=310 ,
P(X=2)=C41C62C103=12 ,
X
0
1
2
3
P
130
310
12
16 ?
P(X=3)=C63C103=16 ,
∴ 的分布列为:
期望 E(X)=95
【解析】
(1)根据去10人中有6人优秀,确定优秀的概率,即可根据对立事件,求出任取3人进行测试,求至少有1人成绩是“优秀”的概率;
(2)求出随机变量X的可能取值和相应的概率,列出分布列,求出数学期望即可.
5.【答案】
(1)解法一:记“甲选手答对 i 道题”为事件 Ai , i=1,2,3 ,“甲选手能晋级”为事件 A ,则 A=A2∪A3 。
P(A)=P(A2∪A3)=P(A2)+P(A3)=C42C21C63+C43C63=45 ;
解法二:(1)记“甲选手能晋级”为事件 A ,则 P(A)=1?C41C22C63=1?15=45 ;
(2)解:设乙选手答对的题目数量为 X ,则 X~B(3,34) ,故 E(X)=3×34=94 ,
设甲选手答对的数量为 Y ,则 Y 的可能取值为 1,2,3 ,
P(Y=1)=C41C22C63=15 , P(Y=2)=C42C21C63=35 , P(Y=3)=C43C63=15 ,
故随机变量 Y 的分布列为
Y
1
2
3
P
15
35
15
所以, E(Y)=1×15+2×35+3×15=2 ,则 E(X)>E(Y) ,
所以,乙选手比甲选手的答题水平高;
【解析】
(1)根据互斥事件概率的加法公式,求出甲选手答对2道题 和3道题的概率,即可得到甲选手晋级的概率;
(2)根据二项分布,代入公式,求出 乙选手答对的题目数量的数学期望,设甲选手答对的数量为 Y , 求出Y的可能取值和相应的概率,列出分布列,求出甲的数学期望进行比较即可.
第七章 随机变量及其分布
7.2离散型随机变量及其分布列
7.2离散型随机变量及其分布列
知识梳理
知识梳理
知识点一 随机变量的概念、表示及特征
概念:一般地,对于随机试验样本空间Ω中的每个样本点ω都有唯一的实数X(ω)与之对应,我们称X为随机变量.
表示:用大写英文字母表示随机变量,如X,Y,Z;用小写英文字母表示随机变量的取值,如x,y,z.
特征:随机试验中,每个样本点都有唯一的一个实数与之对应,随机变量有如下特征:
(1)取值依赖于样本点.
(2)所有可能取值是明确的.
知识点二 随机变量与函数有什么联系和区别?
共同点:随机变量和函数都是一种映射
区别: 随机变量把试验的结果映为实数,函数把实数映为实数
联系:试验结果的范围相当于函数的定义域,随机变量的取值范围相当与函数的值域;
注意:所有随机变量的取值范围的集合叫做随机变量的值域.
知识点三随机变量的分类:
1)离散型随机变量:
对于随机变量可能取的值,如果可以一一列出,这样的随机变量叫做离散型随机变量.
2)连续型随机变量:
随机变量可以取某一区间内的一切值,这样的随机变量叫做连续型随机变量.
知识点四离散型随机变量的分布列及其性质
1.定义:一般地,设离散型随机变量X的可能取值为x1,x2,…,xn,我们称X取每一个值xi的概率P(X=xi)=pi,i=1,2,3,…,n为X的概率分布列,简称分布列.
2.分布列的性质
(1)pi≥0,i=1,2,…,n.
(2)p1+p2+…+pn=1.
题型探究
题型探究
例1.学校趣味运动会上增加了一项射击比赛,比赛规则如下:向A、B两个靶子进行射击,先向A靶射击一次,命中得1分,没有命中得0分;再向B靶连续射击两次,如果只命中一次得2分,一次也没有命中得0分,如果连续命中两次则得5分.甲同学准备参赛,经过一定的训练,甲同学的射击水平显著提高,目前的水平是:向A靶射击,命中的概率是false;向B靶射击,命中的概率为false.假设甲同学每次射击结果相互独立.
(1)求甲同学恰好命中一次的概率;
(2)求甲同学获得的总分X的分布列及数学期望.
【答案】(1)false;(2)分布列见解析;期望为false.
【详解】
(1)记“甲同学恰好命中一次”为事件C,“甲射击命中A靶”为事件D,
“甲第一次射击B靶命中”为事件E,“甲第二次射击B靶命中”为事件F,由题意可知false,false.
由于false,
false.
(2)随机变量X的可能取值为:0,1,2,3,5,6.
false
false
false
false
false
false
X
0
1
2
3
5
6
P
false
false
false
false
false
false
false.
例2.为了响应政府“节能减排”的号召,某知名品牌汽车厂家决定生产一款纯电动汽车.生产前,厂家进行了人们对纯电动汽车接受程度的调查.在20~60岁的人群中随机抽取了100人,调查数据的频率分布直方图和接受纯电动汽车的人数与年龄的统计结果如图所示:
年龄
false
false
false
false
false
接受的人数
false
false
false
false
false
(1)由以上统计数据填false列联表,并判断能否在犯错误的概率不超过false的前提下,认为以false岁为分界点的不同年龄人群对纯电动汽车的接受程度有差异?
false岁以下
false岁及false岁以上
总计
接受
不接受
总计
(2)若以false岁为分界点,从不接受“纯电动汽车”的人群中,按分层抽样的方法抽取false人调查不接受“纯电动汽车”的原因,现从这false人中随机抽取false人.记抽到false岁以下的人数为false,求随机变量false的分布列及数学期望.
false
0.100
0.050
0.010
0.001
false
2.706
3.841
6.635
10.828
附:
false
【答案】(1)联表答案见解析,能在犯错误的概率不超过false的前提下,认为以false岁为分界点的不同人群对“纯电动汽车”的接受程度有差异;(2)分布列答案见解析,数学期望为false.
【详解】
解:(1)由题可得false联表如下:
false岁以下
false岁及false岁以上
总计
接受
35
45
80
不接受
15
5
20
总计
50
50
100
∵false.
∴能在犯错误的概率不超过false的前提下,认为以false岁为分界点的不同人群对“纯电动汽车”的接受程度有差异.
(2)由题意可知,抽取的false人中false岁以下的有false人,false岁及false岁以上的有false人,所以false的可能取值有false,false,false.
falsefalsefalse
所以随机变量false的分布列为:
false
false
false
false
false
false
false
false
false.
例3.某单位招考工作人员,须参加初试和复试,初试通过后组织考生参加复试,共5000人参加复试,复试共三道题,第一题考生答对得3分,答错得0分,后两题考生每答对一道题得5分,答错得0分,答完三道题后的得分之和为考生的复试成绩.
(1)通过分析可以认为考生初试成绩false服从正态分布false,其中false,false,试估计初试成绩不低于90分的人数;
(2)已知某考生已通过初试,他在复试中第一题答对的概率为false,后两题答对的概率均为false,且每道题回答正确与否互不影响.记该考生的复试试成绩为false,求false的分布列及数学期望.
附:若随机变量false服从正态分布false,则false,false,false.
【答案】(1)114人;(2)分布列见解析,false.
【详解】
(1)∵学生笔试成绩false服从正态分布false,其中false,false,
false
∴false
∴估计笔试成绩不低于90分的人数为false人
(2)false的取值分别为0,3,5,8,10,13,
则false
false
false
false
false
false
false的分布为
故false的分布列为:
false
0
3
5
8
10
13
false
false
false
false
false
false
false
false
例4.某篮球职业联赛分为常规赛和季后赛两个阶段.常规赛采用循环赛,分主场比赛和客场比赛两种,积分高的球队进入季后赛;季后赛采用五局三胜制进行淘汰赛,最终决出总冠军.(“false局false胜”制是指先胜false局者获得比赛胜利,比赛结束).下表是甲队在常规赛false场比赛中的比赛结果记录表.
季度
比赛次数
主场次数
获胜次数
主场获胜次数
1季度
23
13
16
11
2季度
27
11
21
8
3季度
30
16
23
13
(1)根据表中信息,能否在犯错误概率不超过false的前提下认为“主客场”与“胜负”之间有关?
(2)已知甲队和乙队在季后赛首轮比赛中相遇,假设每局比赛结果相互独立,以甲队常规赛false场比赛获胜的频率估计甲队在季后赛每局比赛获胜的概率,记false为本轮比赛结束时甲队和乙队所进行的比赛的局数,求false的分布列及甲队获得这轮比赛胜利的概率.
附:false,
P(K2≥k)
0.100
0.050
0.025
k
2.706
3.841
5.024
【答案】(1)不能在犯错误概率不超过false的前提下认为“主客场”与“比赛胜负”之间有关;(2)分布列答案见解析,概率为false.
【详解】
解:(1)根据表格信息列出2×2列联表如下
甲队胜
甲队负
合计
主场
32
8
40
客场
28
12
40
合计
60
20
80
false
所以不能在犯错误概率不超过0.100的前提下认为“主客场”与“比赛胜负”之间有关.
(2)依题意得甲队每局比赛获胜的概率估计值为false,
X的所有可能取值为false,false,false,
false
false
false
所以X的分布列为
X
3
4
5
P
false
false
false
“甲队获得这轮比赛胜利”的概率为false.
例5.抖音是一款音乐创意短视频社交软件,是一个专注年轻人的15秒音乐短视频社区,用户可以通过这款软件选择歌曲,拍摄15秒的音乐短视频,形成自己的作品.2018年6月首批25家央企集体入驻抖音,一调研员在某单位进行刷抖音时间的调查,若该单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人.
(1)应从甲、乙、丙三个部门的员工中分别抽取多少人?
(2)若抽出的7人中有3人是抖音迷,4人为非抖音迷,现从这7人中随机抽取3人做进一步的详细登记.
①用false表示抽取的3人中是抖音迷的员工人数,求随机变量false的分布列与数学期望;
②设false为事件“抽取的3人中,既有是抖音迷的员工,也有非抖音迷的员工’’,求事件false发生的概率.
【答案】(1)应从甲、乙、丙三个部门的员工中分别抽取3人,2人,2人;(2)①分布列详见解析,数学期望为false;(3)false.
【详解】
(1)由已知,甲、乙、丙三个部门的员工人数之比为false由于采用分层抽样的方法从中抽取7人,因此应从甲、乙、丙三个部门的员工中分别抽取3人,2人,2人.
(2)①随机变量X的所有可能取值为0,1,2,3.
false.
false,
false,
false,
false,
所以,随机变量false的分布列为
false
0
1
2
3
false
false
false
false
false
随机变量X的数学期望false.
②设事件false为“抽取的3人中,是抖音迷的员工有1人,非抖音迷的员工有2人”;事件false为“抽取的3人中,是抖音迷的员工有2人,非抖音迷的员工有1人”,则false,且false与false互斥,由(Ⅰ)知false,
false,
故false,
所以事件false发生的概率为false.
课后小练
课后小练
1.甲、乙是两名射击运动员,根据历史统计数据,甲一次射击命中 10 、 9 、 8 环的概率分别为 25 、 25 、 15 ,乙一次射击命中 10 、 9 环的概率分别为 16 、 56 .一轮射击中,甲、乙各射击一次.甲、乙射击相互独立,每次射击也互不影响.
(1)在一轮射击中,求甲命中的环数不高于乙命中的环数的概率;
(2)记一轮射击中,甲、乙命中的环数之和为 X ,求 X 的分布列;
(3)进行三轮射击,求甲、乙命中的环数之和不低于52环的概率.
2.受新冠肺炎疫情影响,本学期同学们在家上网课时间达三个多月,电脑屏幕代替了黑板,对同学们的视力造成了很大的损伤.某学校为了了解同学们现阶段的视力情况,对全校高三1000名学生的视力情况进行了调查,从中随机抽取了100名学生的体检表,绘制了频率分布直方图如图:
(1)求a的值,并估计这1000名学生视力的中位数(精确到0.01);
(2)为了进一步了解视力与学生成绩是否有关,对本年级名次在前50名与后50名的学生进行了调查,得到如下数据:
前50名
后50名
近视
42
32
不近视
8
18
根据表中数据,能否有95%把握认为视力与学习成绩有关?
(3)若报考某高校某专业的资格为:视力不低于5.0,以该样本数据来估计全市高三学生的视力,现从全市视力在4.8以上的同学中随机抽取4名同学,这4名同学中有资格报该校该专业的人数为 X ,求 X 的分布列及数学期望.
P(K2≥k)
0.10
0.05
0.025
0.010
0.005
k
2.706
3.841
5.024
6.635
7.879
3.2020年年初,新冠肺炎疫情防控工作全面有序展开.某社区对居民疫情防控知识进行了网上调研,调研成绩全部都在40分到100分之间.现从中随机选取200位居民的调研成绩进行统计,绘制了如图所示的频率分布直方图.
(1)求a的值,并估计这200位居民调研成绩的中位数;
(2)在成绩为 [40,50] , (90,100] 的两组居民中,用分层抽样的方法抽取6位居民,再从6位居民中随机抽取2位进行详谈.记X为2位居民的调研成绩在 [40,50] 的人数,求随机变量X的分布列.
4.为了了解学生的身体素质情况,现从某校学生中随机抽取10人进行体能测试,测试的分数(百分制)如茎叶图所示,根据有关国家标准成绩不低于79分的为优秀,将频率视为概率.
(1)另从我校学生中任取3人进行测试,求至少有1人成绩是“优秀”的概率;
(Ⅱ)从抽取的这10人(成绩见茎叶图)中随机选取3人,记X表示测试成绩为“优秀”的学生人数,求X的分布列和数学期望.
5.某单位组织“学习强国”知识竞赛,选手从6道备选题中随机抽取3道题.规定至少答对其中的2道题才能晋级.甲选手只能答对其中的4道题。
(1)求甲选手能晋级的概率;
(2)若乙选手每题能答对的概率都是 34 ,且每题答对与否互不影响,用数学期望分析比较甲、乙两选手的答题水平。
答案解析
1.【答案】 (1)解:设一次射击后,甲命中的环数为 ξ ,乙命中的环数为 η ,
则甲命中的环数不高于乙命中的环数为 P(ξ≤η)=P(ξ=8)+P(ξ=9)+P(ξ=10)P(η=10)=15+25+25×16=23 ;
(2)解:题意可知随机变量 X 的可能取值有 17 、 18 、 19 、 20 ,
P(X=17)=15×56=16 , P(X=18)=15×16+25×56=1130 ,
P(X=19)=25×16+25×56=25 , P(X=20)=25×16=115 ,
所以,随机变量 X 的分布列如下表所示:
X
17
18
19
20
P
16
1130
25
115
(3)解:每轮射击后,甲、乙命中的环数之和为17的概率为 p=15×56=16 ,
三轮射击后,甲、乙命中的环数之和最小为 17×3=51 ,
因此,进行三轮射击,求甲、乙命中的环数之和不低于52环的概率为 1?(16)3=215216 .
【解析】(1)设一次射击后,甲命中的环数为 ξ ,乙命中的环数为 η ,由题意可得 P(ξ≤η)=P(ξ=8)+P(ξ=9)+P(ξ=10)P(η=10) ,结合独立事件的概率乘法公式与互斥事件的概率公式可求得所求事件的概率;(2)由题意可知随机变量 X 的可能取值有17、18、19、20,利用独立事件的概率乘法公式可计算得出随机变量 X 在不同取值下的概率,可得出随机变量 X 的分布列;(3)求出每轮射击后,甲、乙命中的环数之和为17的概率,再利用独立事件的概率乘法公式以及对立事件的概率公式可求得所求事件的概率.
2.【答案】 (1)解: (0.25+0.5+2a+1+1.75)×0.2=1 ,所以 a=0.75 ,
视力在4.4以下的频率为: (0.5+0.75)×0.2=0.25 ,
视力在4.6以下的频率为: (0.5+0.75+1.75)×0.2=0.6 ,
所以中位数在4.4至4.6之间,设中位数为 x ,
则 (x?4.4)×1.75=0.5?0.25 , x≈4.54 ,故中位数为4.54.
(2)解:因为 K2 的观测值 k=100(42×18?8×32)250×50×74×26=2500481≈5.2>3.841 ,
所以有95%把握认为视力与学习成绩有关.
(3)解:视力在4.8以上的同学中,视力在5.0以上的同学所占的比例为: 0.250.25+0.75=14
所以从全市视力在4.8以上的同学中随机抽取4名同学,这4名同学中有资格报该校该专业的人数为 X~B(4,14) ,即 P(X=k)=C4k(14)k(34)4?k , k=0,1,2,3,4 ,
所以 P(X=0)=(34)4=81256 ,
P(X=1)=C41×14×(34)3=108256=2764 , P(X=2)=C42×(14)2×(34)2=54256=27128 ,
P(X=3)=C43×(14)3×34=12256=364 , P(X=4)=(14)4=1256 ,
所以 X 的分布列为:
X
0
1
2
3
4
P
81256
2764
27128
364
1256
E(X)=4×14=1 .
【解析】
(1)根据题意由频率分布直方图的性质能求出a和中位数.
(2)首先求出X2≈5.2>3.841,从而有95%把握认为视力与学习成绩有关.
(3)根据题意即可得出视力在4.8以上的同学中,视力在5.0以上的同学所占有比例为14 从全市视力在4.8以上的同学中随机抽取4名同学,这4名同学中有资格报该校专业的人数X~B(4,14) 由此能求出X的分布列和E(X).
3.【答案】 (1)解: (0.005+0.015+0.02+0.025×2+a)×10=1 ,
得 a=0.01 .
前3组的频率之和为 (0.005+0.015+0.02)×10=0.4 ,
第4组的频率为 0.025×10=0.25 ,
因为 0.4+0.25=0.65>0.5 ,所以中位数在第 4 组.
设中位数为 x ,则 (x?70)×0.025=0.1 ,解得 x=74 .
所以200位居民调研成绩的中位数为74分.
(2)解:成绩在 [40,50] , (90,100] 的居民人数分别为10人,20人,
所以在 [40,50] 的居民中应抽取 630×10=2 (人),
在 (90,100] 的居民中应抽取 630×20=4 (人).
X的可能取值为 0 , 1 , 2 ,
P(X=0)=C42C62=25 ,
P(X=1)=C41C21C62=815 ,
P(X=2)=C22C62=115 ,
所以X的分布列为:
X
0
1
2
P
25
815
115
【解析】(1)根据频率之和为1,由此算出a的值,利用频率分布直方图求中位数的方法设中位数为x,列式计算即可得出结论;(2)可知成绩在 [40,50] , (90,100] 的居民人数分别为10人,20人,根据分层抽样,可知抽取的6位中,成绩在 [40,50] 的人数为2人,成绩在 (90,100] 的人数为4人,则x的可能取值为0,1,2,求出相应概率,列出相应的分布列
4.【答案】 (1)解:(1)由茎叶图知,抽取的10人中成绩是“优秀”的有6人,频率为 35 ,依题意,从我校学生中任选1人,成绩是“优秀”的概率为 35 ,记事件 A 表示“在我校学生中任选3人,至少1人成绩是优良”,则 P(A)=1?C33(1?35)3=117125
(Ⅱ)由题意可得, X 的取值可能为0,1,2,3
P(X=0)=C43C103=130 ,
P(X=1)=C42C61C103=310 ,
P(X=2)=C41C62C103=12 ,
X
0
1
2
3
P
130
310
12
16 ?
P(X=3)=C63C103=16 ,
∴ 的分布列为:
期望 E(X)=95
【解析】
(1)根据去10人中有6人优秀,确定优秀的概率,即可根据对立事件,求出任取3人进行测试,求至少有1人成绩是“优秀”的概率;
(2)求出随机变量X的可能取值和相应的概率,列出分布列,求出数学期望即可.
5.【答案】
(1)解法一:记“甲选手答对 i 道题”为事件 Ai , i=1,2,3 ,“甲选手能晋级”为事件 A ,则 A=A2∪A3 。
P(A)=P(A2∪A3)=P(A2)+P(A3)=C42C21C63+C43C63=45 ;
解法二:(1)记“甲选手能晋级”为事件 A ,则 P(A)=1?C41C22C63=1?15=45 ;
(2)解:设乙选手答对的题目数量为 X ,则 X~B(3,34) ,故 E(X)=3×34=94 ,
设甲选手答对的数量为 Y ,则 Y 的可能取值为 1,2,3 ,
P(Y=1)=C41C22C63=15 , P(Y=2)=C42C21C63=35 , P(Y=3)=C43C63=15 ,
故随机变量 Y 的分布列为
Y
1
2
3
P
15
35
15
所以, E(Y)=1×15+2×35+3×15=2 ,则 E(X)>E(Y) ,
所以,乙选手比甲选手的答题水平高;
【解析】
(1)根据互斥事件概率的加法公式,求出甲选手答对2道题 和3道题的概率,即可得到甲选手晋级的概率;
(2)根据二项分布,代入公式,求出 乙选手答对的题目数量的数学期望,设甲选手答对的数量为 Y , 求出Y的可能取值和相应的概率,列出分布列,求出甲的数学期望进行比较即可.
