8.2 一元线性回归模型及其应用 讲义-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(Word含答案)
文档属性
| 名称 | 8.2 一元线性回归模型及其应用 讲义-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(Word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 356.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 17:27:03 | ||
图片预览




文档简介
第八章 成对数据的统计分析
第八章 成对数据的统计分析
8.2一元线性回归模型及其应用
8.2一元线性回归模型及其应用
知识梳理
知识梳理
知识点一 一元线性回归模型
称为Y关于x的一元线性回归模型.其中Y称为因变量或响应变量,x称为自变量或解释变量,a称为截距参数,b称为斜率参数;e是Y与bx+a之间的随机误差,如e=0,那么Y与x之间的关系就可以用一元线性函数模型来描述.
知识点二最小二乘法
线性回归方程与最小二乘法
将=x+称为Y关于x的经验回归方程,也称经验回归函数,其图形称为经验回归直线,这种求经验回归方程的方法叫最小二乘法,求得的,叫做b,a的最小二乘估计,其中=,=-.
知识点三残差与残差分析
残差
对于响应变量Y,通过观测得到的数据称为观测值,通过经验回归方程得到的称为预测值,观测值减去预测值称为残差.
残差分析
残差是随机误差的估计结果,残差的分析可以判断模型刻画数据效果和判断原始数据中是否存在可疑数据等,称为残差分析.
知识点四对模型刻画数据效果的分析
残差图法
残差图中,如残差比较均匀地集中在以横轴为对称轴的水平带状区域内,说明经验回归方程较好地刻画两个变量的关系.
残差平方和法
残差平方和(yi-i)2越小,模型的拟合效果越好.
题型探究
题型探究
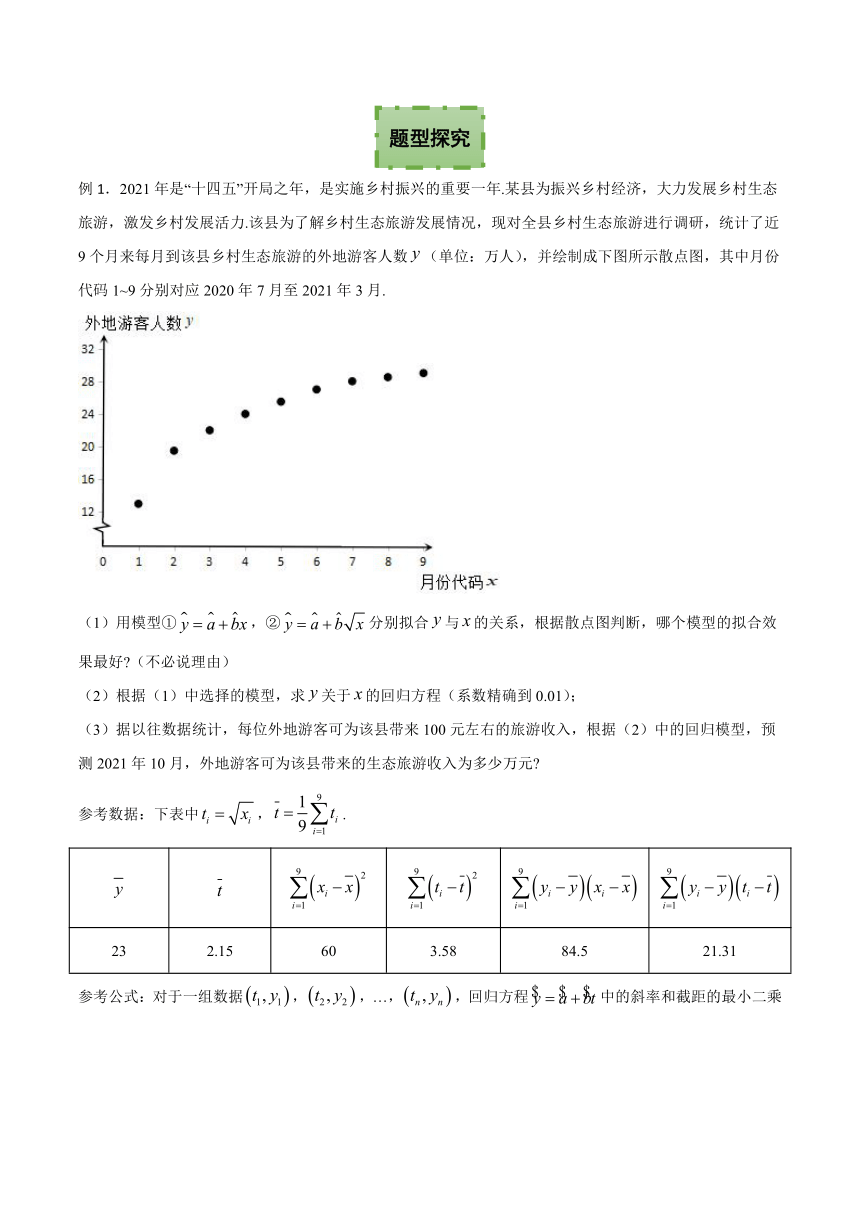
例1.2021年是“十四五”开局之年,是实施乡村振兴的重要一年.某县为振兴乡村经济,大力发展乡村生态旅游,激发乡村发展活力.该县为了解乡村生态旅游发展情况,现对全县乡村生态旅游进行调研,统计了近9个月来每月到该县乡村生态旅游的外地游客人数false(单位:万人),并绘制成下图所示散点图,其中月份代码1~9分别对应2020年7月至2021年3月.
(1)用模型①false,②false分别拟合false与false的关系,根据散点图判断,哪个模型的拟合效果最好?(不必说理由)
(2)根据(1)中选择的模型,求false关于false的回归方程(系数精确到0.01);
(3)据以往数据统计,每位外地游客可为该县带来100元左右的旅游收入,根据(2)中的回归模型,预测2021年10月,外地游客可为该县带来的生态旅游收入为多少万元?
参考数据:下表中false,false.
false
false
false
false
false
false
23
2.15
60
3.58
84.5
21.31
参考公式:对于一组数据false,false,…,false,回归方程false中的斜率和截距的最小二乘估计公式分别为false,false.
【答案】(1)模型②false的拟合效果最好;(2)false;(3)3400万元.
【详解】
(1)模型②false的拟合效果最好.
(2)令false,知false与false可用线性方false拟合,则
false,false,
所以,false关于false的线性回归方程为false,
故false关于x的回归方程为false.
(3)2021年10月,即false时,false(万人),
此时,外地游客可为该县带来的生态旅游收入为3400万元.
例2.2021年,我国脱贫攻坚战取得了全面胜利.为了巩固拓展脱贫攻坚成果,不断提高群众的幸福感,某县继续推进山羊养殖项目.为了建设相应的配套项目,该县主管部门对该县近年来山羊养殖业的规模进行了跟踪调查,得到了该县每年售卖山羊数量false(单位:万只)与相应年份代码false的数据如下表:
年份
2015
2016
2017
2018
2019
2020
年份代码false
1
2
3
4
5
6
售卖山羊数量false(万只)
11
13
16
15
20
21
(1)由表可知false与false有较强的线性相关关系,求false关于false的线性回归方程;
(2)已知该县养殖的山羊品种只有甲、乙两种,且甲品种山羊与乙品种山羊的数量之比为false,甲品种山羊达到售卖标准后的出售价为2500元/只,乙品种山羊达到售卖标准后的出售价为2700元/只.为了解养殖山羊所需要的时间,该县主管部门随机抽取了甲品种山羊和乙品种山羊各100只进行调查,得到要达到售卖标准所需的养殖时间如下表:
养殖时间(月数)
6
7
8
9
甲品种山羊(只)
20
35
35
10
乙品种山羊(只)
10
30
40
20
以上述样本统计的养殖山羊所需时间情况估计全县养殖山羊所需时间(即以各养殖时间的频率作为各养殖时间的概率),且每月每只山羊的养殖成本为300元,结合(1)中所求回归方程,试求2022年该县养殖山羊所获利润的期望(假设山羊达到售卖标准后全部及时卖完).(利润=卖山羊的收入一山羊的养殖成本)
参考公式及数据:回归直线方程为false,其中false,false.
【答案】(1)false;(2)8800万元.
【详解】
(1)因为false,false,
所以false,
可得false.
所以false与false之间的线性回归方程为false.
(2)由false可知,当false时,可得false,
其中甲品种山羊有false万只,乙品种山羊有false万只.
由频率估计概率,可得甲品种山羊达到售卖标准需要的养殖时间为6个月,7个月,8个月和9个月的概率分别为0.2,0.35,0.35和0.1,
所以甲品种山羊要达到售卖标准需要养殖时间的期望为false(月).
由频率估计概率,可得乙品种山羊达到售卖标准需要的养殖时间为6个月,7个月,8个月和9个月的概率分别为0.1,0.3,0.4和0.2,
所以乙品种山羊要达到售卖标准需要养殖时间的期望为false(月).
养殖每只甲品种山羊利润的期望为false(元),
养殖每只乙品种山羊利润的期望为false(元),
故2022年该县售卖的山羊所获利润的期望为false(万元).
例3.false年false月false日,在全国脱贫攻坚总结表彰大会上,习近平总书记庄严宣告:我国脱贫攻坚战取得全面胜利.目前,河南省false个贫困县已经全部脱贫摘帽,退出贫困县序列.false年起,我省某贫困地区创新开展产业扶贫,响应第三产业的扶贫攻坚政策,经济收入逐年增加.该地的经济收入变化及构成比例如图所示:
年份
false年
false年
false年
false年
false年
年份代号false
false
false
false
false
false
经济收入false
(单位:百万元)
false
false
false
false
false
(1)根据以上图表,试分析:与false年相比,false年第三产业与种植业收入变化情况;
(2)求经济收入false关于false的线性回归方程,并预测false年该地区的经济收入.
参考公式:对于一组具有线性相关关系的数据falsefalse,其回归直线false的斜率和截距的最小二乘估计分别为:false,false.
【答案】(1)答案见解析;(2)false;false年该地区的经济收入预测为false百万元.
【详解】
解:(1)①与false年相比,false年第三产业的收入占比大幅度增加;
②false年第三产业的收入为false百万元,false年第三产业的收入为false百万元,收入大幅度增加;
③与false年相比,种植业收入占比减少,但种植业收入依然保持增长;
(2)由表格中的数据可知,false,false,
false,false,
则false,
所以false,
故经济收入false关于false的线性回归方程为false,
当false时,false,则false年该地区的经济收入预测为false百万元.
例4.随着工业化以及城市车辆的增加,城市的空气污染越来越严重,空气质量指数API一直居高不下,对人体的呼吸系统造成了严重的影响.现调查了某市500名居民的工作场所和呼吸系统健康情况,得到2×2列联表如下:
?
室外工作
室内工作
总计
有呼吸系统疾病
150
?
?
无呼吸系统疾病
?
100
?
总 计
200
?
?
(1)补全2×2列联表;
(2)能否在犯错误的概率不超过0.05的前提下认为感染呼吸系统疾病与工作场所有关?
(3)现采用分层抽样从室内工作的居民中抽取一个容量为6的样本,将该样本看成一个总体,从中随机地抽取两人,求两人都有呼吸系统疾病的概率.
【答案】(1)列联表见解析;(2)能在犯错误的概率不超过0.05的前提下认为感染呼吸系统疾病与工作场所有关;(3)false.
【详解】
(1)列联表如下:
?
室外工作
室内工作
总计
有呼吸系统疾病
150
200
350
无呼吸系统疾病
50
100
150
总 计
200
300
500
(2)χ2=false≈3.968>3.841.
所以能在犯错误的概率不超过0.05的前提下认为感染呼吸系统疾病与工作场所有关.
(3)采用分层抽样从室内工作的居民中抽取6名,其中有呼吸系统疾病的抽4人,无呼吸系统疾病的抽2人,设A为“从中随机地抽取两人,两人都有呼吸系统疾病”,则
P(A)=false.
例5.为确保我国如期全面建成小康社会,实现第一个百年奋斗目标打下了坚实的基础.在产业扶贫政策的大力支持下,某玩具厂对原有的生产线进行技术升级,为了更好地对比升级前和升级后的效果,其中甲生产线继续使用旧的生产模式,乙生产线采用新的生产模式.质检部门随机抽检了甲、乙两条生产线的各100件玩具,在抽取的200件玩具中,根据检测结果将它们分为“A”、“B”、“C”三个等级,false等级都是合格品,C等级是次品,统计结果如表所示:
等级
A
B
C
频数
100
75
25
(表二)
合格品
次品
合计
甲
80
乙
5
合计
在相关政策扶持下,确保每件合格品都有对口销售渠道,但从安全起见,所有的次品必须由厂家自行销毁.
(1)请根据所提供的数据,完成上面的false列联表(表二),并判断是否有false的把握认为产品的合格率与技术升级有关?
(2)每件玩具的生产成本为20元,false等级产品的出厂单价分别为m元、40元.若甲生产线抽检的玩具中有35件为A等级,用样本的频率估计概率,若进行技术升级后,平均生产一件玩具比技术升级前多盈利12元,则A等级产品的出产单价为多少元?
附:false,其中false.
false
0.05
0.025
0.010
0.005
0.001
false
3.841
5.024
6.635
7.879
10.828
【答案】(1)列联表见解析;有false的把握认为产品的合格率与技术升级有关;(2)60元.
【详解】
解:(1)根据所提供的数据,可得false列联表:
合格品
次品
合计
甲
80
20
100
乙
95
5
100
合计
175
25
200
设false产品的合格率与技术升级无关.
由false,
可得false.
false,故有false的把握认为产品的合格率与技术升级有关.
(2)法一:甲生产线抽检的产品中有35件false等级,45件false等级,20件false等级,
对于甲生产线,单件产品利润false的取值可能为false,
false的分布列如下:
false
false
20
false
false
false
false
false
则false,
乙生产线抽检的产品中有65件false等级,30件false等级,5件false等级;
对于乙生产线,单位产品利润false的取值可能为false,
false的分布列如下:
false
false
20
false
false
false
false
false
则false,
依题意.false,
false,所以,false等级产品的出产单价为60元.
法二:甲生产线抽检的产品中有35件false等级,45件false等级,20件false等级,
乙生产线抽检的产品中有65件false等级,30件false等级,5件false等级;
因为用样本的频率估计概率
所以对于甲生产线,单件产品的利润false
对于乙生产线,单件产品的利润false
依题意.false,
false,所以,false等级产品的出产单价为60元.
课后小练
课后小练
1.为了迎接十四运,提高智慧城市水平,西安公交公司近期推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,x表示活动推出的天数,y表示每天使用扫码支付的人次(单位:十人次),统计数据如表下所示:
x
1
2
3
4
5
6
7
y
6
11
21
34
66
101
196
根据以上数据,绘制了散点图.
(1)根据散点图判断,在推广期内, y=a+bx 与 y=c?dx ( c,?d 均为大于零的常数),哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由);
(2)根据(1)的判断结果及表1中的数据,建立y与x的回归方程,并预测活动推出第8天使用扫码支付的人次;
(3)推广期结束后,车队对乘客的支付方式进行统计,结果如下表:
支付方式
现金
乘车卡
扫码
比例
10%
60%
30%
西安公交六公司车队为缓解周边居民出行压力,以90万元的单价购进了一批新车,根据以往的经验可知,每辆车每个月的运营成本约为0.66万元.已知该线路公交车票价为2元,使用现金支付的乘客无优惠,使用乘车卡支付的乘客享受8折优惠,扫码支付的乘客随机优惠,根据统计结果得知,使用扫码支付的乘客中有 16 的概率享受7折优惠,有 13 的概率享受8折优惠,有 12 的概率享受9折优惠.预计该车队每辆车每个月有2万人次乘车,根据所给数据以事件发生的频率作为相应事件发生的概率,在不考虑其它因素的条件下,按照上述收费标准,请你估计这批车辆需要几年(结果取整数年)才能盈利?
参考数据:
y
v
i=17xiyi
i=17xivi
100.54
62.14
1.54
2535
50.12
3.47
其中其中 vi=lgyi , v=17i=17vi ,
参考公式:对于一组数据 (u1,?v1) , (u2,?v2) ,…, (un,?vn) ,其回归直线 v=α+βu 的斜率和截距的最小二乘估计公式分别为: β=i=1nuivi?nu?vi=1nui2?nu2 , α=v?βu .
2.某公司为一所山区小学安装了价值2万元的一台饮用水净化设备,每年都要为这台设备支出保养维修费用,我们称之为设备年度保养维修费.下表是该公司第 x 年为这台设备支出的年度保养维修费 y (单位:千元)的部分数据:
x
2
3
4
5
6
y
2.1
3.4
5.9
6.6
7.0
画出散点图如下:
通过计算得 y 与 x 的相关系数 r≈0.96 .由散点图和相关系数 r 的值可知, y 与 x 的线性相关程度很高.
附: b=i=1n(xi?x)(yi?y)i=1n(xi?x)2 , a=y?bx .
(1)建立 y 关于 x 的线性回归方程 y=bx+a ;
(2)若设备年度保养维修费不超过1.93万元就称该设备当年状态正常,根据(1)得到的线性回归方程,估计这台设备有多少年状态正常?
3.2021年2月25日,在全国脱贫攻坚总结表彰大会上,习近平总书记庄严宣告:我国脱贫攻坚战取得全面胜利.目前,陕西省56个贫困县已经全部脱贫摘帽,退出贫困县序列.2016年起,我省某贫困地区创新开展产业扶贫,响应第三产业的扶贫攻坚政策,经济收入逐年增加.该地的经济收入变化及构成比例如下表所示:
年份
2016年
2017年
2018年
2019年
2020年
年份代号 x
1
2
3
4
5
经济收人 y (单位:百万元)
5
8
13
18
20
2016年?2020年经济收入构成比例:
年份
类别
种植收人
养殖收人
第三产业收人
其他收人
2016年
60%
30%
6%
4%
2020年
34%
30%
30%
6%
参考公式:对于一组具有线性相关关系的数据 (xi,yi)(i=1,2,3,?,n) ,其回归直线 y=bx+a 的斜率和截距的最小二计分别为 b=i=1n(xi?x)(yi?y)i=1n(xi?x)2=i=1nxiyi?nxyi=1nxi2?nx2,a=y?bx
(1)根据上表,试分析:与2016年相比,2020年第三产业?种植业收入变化情况;
(2)求经济收入y关于x的线性回归方程,并预测2025年该地区的经济收入.
4.某公司研发了一种帮助家长解决孩子早教问题的萌宠机器人.萌宠机器人语音功能让它就像孩子的小伙伴一样和孩子交流,记忆功能还可以记住宝宝的使用习惯,很快找到宝宝想听的内容.同时提供快乐儿歌、国学经典、启蒙英语等早期教育内容,且云端内容可以持续更新.萌宠机器人一投放市场就受到了很多家长欢迎.为了更好地服务广大家长,该公司研究部门从流水线上随机抽取100件萌宠机器人(以下简称产品),统计其性能指数并绘制频率分布直方图(如图1):
产品的性能指数在 [50,70) 的适合托班幼儿使用(简称A类产品),在 [70,90) 的适合小班和中班幼儿使用(简称B类产品),在 [90,110] 的适合大班幼儿使用(简称C类产品),A,B,C,三类产品的销售利润分别为每件1.5,3.5,5.5(单位:元).以这100件产品的性能指数位于各区间的频率代替产品的性能指数位于该区间的概率.
参考公式:对于一组数据 (u1,υ1),(u2,υ2),?,(un,υn) ,其回归直线 υ=α+βu 的斜率和截距的最小二乘估计分别为 β=i=1n(ui?u)(υi?υ)i=1n(ui?u)2 , α=υ?βu .
(1)求每件产品的平均销售利润;
(2)该公司为了解年营销费用 x (单位:万元)对年销售量 y (单位:万件)的影响,对近5年的年营销费用 xi ,和年销售量 yi(i=1,2,3,4,5) 数据做了初步处理,得到的散点图(如图2)及一些统计量的值.
i=15ui
i=15υi
i=15(ui?u)(υi?υ)
i=15(ui?u)2
16.30
24.87
0.41
1.64
表中 ui=lnxi , υi=lnyi , u=15i=15ui , υ=15i=15υi .
根据散点图判断, y=a?xb 可以作为年销售量 y (万件)关于年营销费用 x (万元)的回归方程.
(i)建立 y 关于 x 的回归方程;
(ii)用所求的回归方程估计该公司应投入多少营销费,才能使得该产品一年的收益达到最大?
(收益=销售利润-营销费用,取 e4.159=64 ).
5.某地一公司的市场研究人员为了解公司生产的某产品的使用情况,从两个方面进行了调查统计,一是产品的质量参数x,二是产品的使用时间t(单位:千小时),经统计分析,质量参数x服从正态分布 N(0.8,0.0152) ,使用时间t与质量参数x之间有如下关系:
质量参数x
0.65
0.70
0.75
0.80
0.85
0.90
0.95
使用时间t
2.60
2.81
3.05
3.10
3.25
3.35
3.54
附:参考数据: x=0.8,t=3.1,i=17xi2=4.55,i=17ti2=67.88,0.115=0.339 .若 ξ?N(μ,σ2) ,则 P(μ?σ<ξ≤μ+σ)=0.6828,P(μ?2σ<ξ≤μ+2σ)=0.9544
参考公式:相关系数 r=i=1n(xi?x)(ti?t)i=1n(xi?x)2i=1n(ti?t)2 ;
回归直线方程为 t=bx+a ,其中 b=i=1n(xi?x)(ti?t)i=1n(xi?x)2,a=y?bx .
(1)该地监管部门对该公司的该产品进行检查,要求质量参数在0.785以上的产品为合格产品.现抽取20件该产品进行校验,求合格产品的件数的数学期望;
(2)该公司研究人员根据最小二乘法求得线性回归方程为 t=2.92x+0.76 ,请用相关系数说明使用时间t与质量参数x之间的关系是否可用线性回归模型拟合.
答案解析
【答案】
(1)根据散点图判断,在推广期内, y=c?dx ( c,?d 均为大于零的常数),适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型;
(2)根据(1)的判断结果 y=c?dx ,两边取对数得: lgy=lgc+lgd?x ,
其中 vi=lgyi , v=17i=17vi=1.54 , i=17xivi=50.12 , x=4 , i=17xi2=140 ,
∴β=lgd=i=17xivi?nx?vi=1nxi2?nx2=0.25 , α=lgc=v?βx=0.54 ,
∴lgy=0.54+0.25x , ∴y=100.54+0.25?x=3.47×100.25x .
当 x=8 时, y=100.54+0.25?8=3.47×102=347 ,
∴活动推出第8天使用扫码支付的人次为3470人;
(3)设一名乘客一次乘车的费用为 ξ 元,
由题意知: ξ 所有可能取值为:1.4,1.6,1.8,2,
∴P(ξ=1.4)=0.3×16=0.05 , P(ξ=1.6)=0.6+0.3×13=0.7 , P(ξ=1.8)=0.3×12=0.15 , P(ξ=2)=0.1 ,
∴E(ξ)=1.4×0.05+1.6×0.7+1.8×0.15+2×0.1=1.66 ,
假设这批车需要 n(n∈N?) 年才能开始盈利,则 1.66×2×12×n≥90+0.66×12×n ,
解得: n≥2.82 ,∴需要3年才能盈利.
【解析】
(1)根据散点图知 y=c?dx适宜作 y与x 的回归方程类型;
(2)对 y=c?dx两边同时取常用对数,化为线性回归方程,求出对应的系数,写出 y与x 的回归方程,再利用方程求出x=8时对应的函数值.
2.【答案】
(1)解: x=15×(2+3+4+5+6)=4 ,
y=15×(2.1+3.4+5.9+6.6+7)=5 .
b=i=15(xi?x)(yi?y)i=15(xi?x)2=1310=1.3 .
∴a=y?bx=5?1.3×4=?0.2 .
∴ 线性回归方程为 y=1.3x?0.2 .
(2)解:设这台设备有 x 年状态正常,由已知得 y≤19.3 ,即 1.3x?0.2≤19.3 .
解 1.3x?0.2≤19.3 得 x≤15 .
∴ 估计该设备有 15 年状态正常
【解析】
(1)根据已知条件求出x=15×(2+3+4+5+6)=4y=15×(2.1+3.4+5.9+6.6+7)=5 , 再根据公式可求出 ?b^,a^即可得出 ?y?关于?x?的线性回归方程;?
(2) 设这台设备有?x?年状态正常,由已知得?y≤19.3?,即?1.3x?0.2≤19.3?解不等式即可得出。
3.【答案】 (1)解:①与2016年相比,2020年第三产业的收入占比大幅度增加;2016年第三产业的收入为0.3百万元,2020年第三产业的收入为6百万元,收入大幅度增加;
②与2016年相比,种植业收入占比减少,但种植业收入依然保持增长;
(2)解: x=1+2+3+4+55=3,y=5+8+13+18+205=12.8
i=15xi2=12+22+32+42+52=55,i=15xiyi=1×5+2×8+3×13+4×18+5×20=232 b∧=i=15xiyi?5xyi=15xi2?5x2=232?5×3×12.855?5×3×3=4
∴a=y?bx=12.8?4×3=0.8
故经济收入 y 关于 x 的线性回归方程为 y=0.8+4x.
当 x=10 时, y=40.8 ,则2025年该地区的经济收入预测为40.8百万元.
【解析】
直接由表格中数据分析与2016 年相比, 2020年第三产业、种植业收入变化情况即可。
(2) 由已知数据求得 a^与b^的值 可得线性回归方程,取 x=10 求得 y^ 可得2025年该地区的经济收入.
4.【答案】
(1)解:设每件产品的销售利润为 ξ 元,则 ξ 的所有可能取值为1.5,3.5,5.5,
由直方图可得, A , B , C 三类产品的频率分别为0.15、0.45、0.4,
所以, P(ξ=1.5)=0.15 , P(ξ=3.5)=0.45 , P(ξ=5.5)=0.4 ,
所以随机变量 ξ 的分布列为:
ξ
1.5
3.5
5.5
P
0.15
0.45
0.4
所以, Eξ=1.5×0.15+3.5×0.45+5.5×0.4=4 ,
故每件产品的平均销售利润为4元;
(2)解:(i)由 y=a?xb 得, lny=ln(a?xb)=lna+blnx ,
令 u=lnx , υ=lny , c=lna ,则 υ=c+bu ,
由表中数据可得, b=i=15(ui?u)(υi?υ)i=15(ui?u)2=0.411.61=0.25 ,
则 c=υ?bu=24.875?0.25×16.305=4.159 ,
所以, υ=4.159+0.25u ,
即 lny=4.159+0.25lnx=ln(e4.159?x14) ,
因为 e4.159=64 ,所以 y=64x14 ,
故所求的回归方程为 y=64x14 ;
(ii)设年收益为 z 万元,则 z=(Eξ)?y?x=256x14?x ,
设 t=x14 , f(t)=256t?t4 ,
则 f'(t)=256?4t3=4(64?t3) ,
当 t∈(0,4) 时, f'(t)>0 , f(t) 在 (0,4) 单调递增,
当 t∈(4,+∞) 时, f'(t)<0 , f(t) 在 (4,+∞) 单调递减,
所以,当 t=4 ,即 x=256 时, z 有最大值为768,
即该厂应投入256万元营销费,能使得该产品一年的收益达到最大768万元.
【解析】
(1)设每件产品的销售利润为ξ元,则ξ的所有可能取值为1.5,3.5,5.5,求出概率,得到分布列,然后求解期望;
(2)(i)由y=a?xb得,lny=ln(a?xb)=lna+blnx,令u=lnx,υ=lny,c=lna,可得υ=c+bu,求出回归直线方程的系数,然后求解y关于x的回归方程;
(ii)设年收益为z万元,则 z=(Eξ)?y?x=256x14?x?, 利用换元法,以及函数的导数,判断函数的单调性,求解函数的最值,推出结果.
5.【答案】
(1)解:一件产品的质量参数在0.785以上的概率 p=1?1?0.68282=0.8414 ,
设抽取20件该产品中为合格产品的件数为 ξ ,则 ξ~B(20?,?0.8414) ,
则 E(ξ)=20×0.8414=16.828 .
(2)解: i=1n(xi?x)2=i=1nxi2?2xi=1nxi+nx2=i=1nxi2?2x?nx+nx2=i=1nxi2?nx2 ,
同理, i=1n(ti?t)2==i=1nti2?nt2 ,
∵b=i=1n(xi?x)(ti?t)i=1n(xi?x)2 , ∴i=1n(xi?x)(ti?t)=bi=1n(xi?x)2 ,
∴r=i=1n(xi?x)(ti?t)i=1n(xi?x)2(ti?t)2=bi=1n(xi?x)2i=1n(xi?x)2(ti?t)2=bi=1n(xi?x)2i=1n(ti?t)2
=bi=1nxi2?nx2i=1nti2?nt2=2.92×4.55?7×0.8267.88?7×3.12=2.92×0.070.61
=2.92×0.114=2.92×0.337≈0.98
所以使用时间 t 与质量参数 x 之间具有较强的线性相关关系,可用线性回归模型拟合.
【解析】
(1)根据题意由概率的定义结合已知条件求出结果,再由正太分布的数值结合期望公式计算出答案即可。
(2)结合已知条件把数值代入到公式计算出参考数据,由此得到线性回归方程并代入数值计算出 使用时间 t 与质量参数 x 之间具有较强的线性相关关系,可用线性回归模型拟合.
第八章 成对数据的统计分析
8.2一元线性回归模型及其应用
8.2一元线性回归模型及其应用
知识梳理
知识梳理
知识点一 一元线性回归模型
称为Y关于x的一元线性回归模型.其中Y称为因变量或响应变量,x称为自变量或解释变量,a称为截距参数,b称为斜率参数;e是Y与bx+a之间的随机误差,如e=0,那么Y与x之间的关系就可以用一元线性函数模型来描述.
知识点二最小二乘法
线性回归方程与最小二乘法
将=x+称为Y关于x的经验回归方程,也称经验回归函数,其图形称为经验回归直线,这种求经验回归方程的方法叫最小二乘法,求得的,叫做b,a的最小二乘估计,其中=,=-.
知识点三残差与残差分析
残差
对于响应变量Y,通过观测得到的数据称为观测值,通过经验回归方程得到的称为预测值,观测值减去预测值称为残差.
残差分析
残差是随机误差的估计结果,残差的分析可以判断模型刻画数据效果和判断原始数据中是否存在可疑数据等,称为残差分析.
知识点四对模型刻画数据效果的分析
残差图法
残差图中,如残差比较均匀地集中在以横轴为对称轴的水平带状区域内,说明经验回归方程较好地刻画两个变量的关系.
残差平方和法
残差平方和(yi-i)2越小,模型的拟合效果越好.
题型探究
题型探究
例1.2021年是“十四五”开局之年,是实施乡村振兴的重要一年.某县为振兴乡村经济,大力发展乡村生态旅游,激发乡村发展活力.该县为了解乡村生态旅游发展情况,现对全县乡村生态旅游进行调研,统计了近9个月来每月到该县乡村生态旅游的外地游客人数false(单位:万人),并绘制成下图所示散点图,其中月份代码1~9分别对应2020年7月至2021年3月.
(1)用模型①false,②false分别拟合false与false的关系,根据散点图判断,哪个模型的拟合效果最好?(不必说理由)
(2)根据(1)中选择的模型,求false关于false的回归方程(系数精确到0.01);
(3)据以往数据统计,每位外地游客可为该县带来100元左右的旅游收入,根据(2)中的回归模型,预测2021年10月,外地游客可为该县带来的生态旅游收入为多少万元?
参考数据:下表中false,false.
false
false
false
false
false
false
23
2.15
60
3.58
84.5
21.31
参考公式:对于一组数据false,false,…,false,回归方程false中的斜率和截距的最小二乘估计公式分别为false,false.
【答案】(1)模型②false的拟合效果最好;(2)false;(3)3400万元.
【详解】
(1)模型②false的拟合效果最好.
(2)令false,知false与false可用线性方false拟合,则
false,false,
所以,false关于false的线性回归方程为false,
故false关于x的回归方程为false.
(3)2021年10月,即false时,false(万人),
此时,外地游客可为该县带来的生态旅游收入为3400万元.
例2.2021年,我国脱贫攻坚战取得了全面胜利.为了巩固拓展脱贫攻坚成果,不断提高群众的幸福感,某县继续推进山羊养殖项目.为了建设相应的配套项目,该县主管部门对该县近年来山羊养殖业的规模进行了跟踪调查,得到了该县每年售卖山羊数量false(单位:万只)与相应年份代码false的数据如下表:
年份
2015
2016
2017
2018
2019
2020
年份代码false
1
2
3
4
5
6
售卖山羊数量false(万只)
11
13
16
15
20
21
(1)由表可知false与false有较强的线性相关关系,求false关于false的线性回归方程;
(2)已知该县养殖的山羊品种只有甲、乙两种,且甲品种山羊与乙品种山羊的数量之比为false,甲品种山羊达到售卖标准后的出售价为2500元/只,乙品种山羊达到售卖标准后的出售价为2700元/只.为了解养殖山羊所需要的时间,该县主管部门随机抽取了甲品种山羊和乙品种山羊各100只进行调查,得到要达到售卖标准所需的养殖时间如下表:
养殖时间(月数)
6
7
8
9
甲品种山羊(只)
20
35
35
10
乙品种山羊(只)
10
30
40
20
以上述样本统计的养殖山羊所需时间情况估计全县养殖山羊所需时间(即以各养殖时间的频率作为各养殖时间的概率),且每月每只山羊的养殖成本为300元,结合(1)中所求回归方程,试求2022年该县养殖山羊所获利润的期望(假设山羊达到售卖标准后全部及时卖完).(利润=卖山羊的收入一山羊的养殖成本)
参考公式及数据:回归直线方程为false,其中false,false.
【答案】(1)false;(2)8800万元.
【详解】
(1)因为false,false,
所以false,
可得false.
所以false与false之间的线性回归方程为false.
(2)由false可知,当false时,可得false,
其中甲品种山羊有false万只,乙品种山羊有false万只.
由频率估计概率,可得甲品种山羊达到售卖标准需要的养殖时间为6个月,7个月,8个月和9个月的概率分别为0.2,0.35,0.35和0.1,
所以甲品种山羊要达到售卖标准需要养殖时间的期望为false(月).
由频率估计概率,可得乙品种山羊达到售卖标准需要的养殖时间为6个月,7个月,8个月和9个月的概率分别为0.1,0.3,0.4和0.2,
所以乙品种山羊要达到售卖标准需要养殖时间的期望为false(月).
养殖每只甲品种山羊利润的期望为false(元),
养殖每只乙品种山羊利润的期望为false(元),
故2022年该县售卖的山羊所获利润的期望为false(万元).
例3.false年false月false日,在全国脱贫攻坚总结表彰大会上,习近平总书记庄严宣告:我国脱贫攻坚战取得全面胜利.目前,河南省false个贫困县已经全部脱贫摘帽,退出贫困县序列.false年起,我省某贫困地区创新开展产业扶贫,响应第三产业的扶贫攻坚政策,经济收入逐年增加.该地的经济收入变化及构成比例如图所示:
年份
false年
false年
false年
false年
false年
年份代号false
false
false
false
false
false
经济收入false
(单位:百万元)
false
false
false
false
false
(1)根据以上图表,试分析:与false年相比,false年第三产业与种植业收入变化情况;
(2)求经济收入false关于false的线性回归方程,并预测false年该地区的经济收入.
参考公式:对于一组具有线性相关关系的数据falsefalse,其回归直线false的斜率和截距的最小二乘估计分别为:false,false.
【答案】(1)答案见解析;(2)false;false年该地区的经济收入预测为false百万元.
【详解】
解:(1)①与false年相比,false年第三产业的收入占比大幅度增加;
②false年第三产业的收入为false百万元,false年第三产业的收入为false百万元,收入大幅度增加;
③与false年相比,种植业收入占比减少,但种植业收入依然保持增长;
(2)由表格中的数据可知,false,false,
false,false,
则false,
所以false,
故经济收入false关于false的线性回归方程为false,
当false时,false,则false年该地区的经济收入预测为false百万元.
例4.随着工业化以及城市车辆的增加,城市的空气污染越来越严重,空气质量指数API一直居高不下,对人体的呼吸系统造成了严重的影响.现调查了某市500名居民的工作场所和呼吸系统健康情况,得到2×2列联表如下:
?
室外工作
室内工作
总计
有呼吸系统疾病
150
?
?
无呼吸系统疾病
?
100
?
总 计
200
?
?
(1)补全2×2列联表;
(2)能否在犯错误的概率不超过0.05的前提下认为感染呼吸系统疾病与工作场所有关?
(3)现采用分层抽样从室内工作的居民中抽取一个容量为6的样本,将该样本看成一个总体,从中随机地抽取两人,求两人都有呼吸系统疾病的概率.
【答案】(1)列联表见解析;(2)能在犯错误的概率不超过0.05的前提下认为感染呼吸系统疾病与工作场所有关;(3)false.
【详解】
(1)列联表如下:
?
室外工作
室内工作
总计
有呼吸系统疾病
150
200
350
无呼吸系统疾病
50
100
150
总 计
200
300
500
(2)χ2=false≈3.968>3.841.
所以能在犯错误的概率不超过0.05的前提下认为感染呼吸系统疾病与工作场所有关.
(3)采用分层抽样从室内工作的居民中抽取6名,其中有呼吸系统疾病的抽4人,无呼吸系统疾病的抽2人,设A为“从中随机地抽取两人,两人都有呼吸系统疾病”,则
P(A)=false.
例5.为确保我国如期全面建成小康社会,实现第一个百年奋斗目标打下了坚实的基础.在产业扶贫政策的大力支持下,某玩具厂对原有的生产线进行技术升级,为了更好地对比升级前和升级后的效果,其中甲生产线继续使用旧的生产模式,乙生产线采用新的生产模式.质检部门随机抽检了甲、乙两条生产线的各100件玩具,在抽取的200件玩具中,根据检测结果将它们分为“A”、“B”、“C”三个等级,false等级都是合格品,C等级是次品,统计结果如表所示:
等级
A
B
C
频数
100
75
25
(表二)
合格品
次品
合计
甲
80
乙
5
合计
在相关政策扶持下,确保每件合格品都有对口销售渠道,但从安全起见,所有的次品必须由厂家自行销毁.
(1)请根据所提供的数据,完成上面的false列联表(表二),并判断是否有false的把握认为产品的合格率与技术升级有关?
(2)每件玩具的生产成本为20元,false等级产品的出厂单价分别为m元、40元.若甲生产线抽检的玩具中有35件为A等级,用样本的频率估计概率,若进行技术升级后,平均生产一件玩具比技术升级前多盈利12元,则A等级产品的出产单价为多少元?
附:false,其中false.
false
0.05
0.025
0.010
0.005
0.001
false
3.841
5.024
6.635
7.879
10.828
【答案】(1)列联表见解析;有false的把握认为产品的合格率与技术升级有关;(2)60元.
【详解】
解:(1)根据所提供的数据,可得false列联表:
合格品
次品
合计
甲
80
20
100
乙
95
5
100
合计
175
25
200
设false产品的合格率与技术升级无关.
由false,
可得false.
false,故有false的把握认为产品的合格率与技术升级有关.
(2)法一:甲生产线抽检的产品中有35件false等级,45件false等级,20件false等级,
对于甲生产线,单件产品利润false的取值可能为false,
false的分布列如下:
false
false
20
false
false
false
false
false
则false,
乙生产线抽检的产品中有65件false等级,30件false等级,5件false等级;
对于乙生产线,单位产品利润false的取值可能为false,
false的分布列如下:
false
false
20
false
false
false
false
false
则false,
依题意.false,
false,所以,false等级产品的出产单价为60元.
法二:甲生产线抽检的产品中有35件false等级,45件false等级,20件false等级,
乙生产线抽检的产品中有65件false等级,30件false等级,5件false等级;
因为用样本的频率估计概率
所以对于甲生产线,单件产品的利润false
对于乙生产线,单件产品的利润false
依题意.false,
false,所以,false等级产品的出产单价为60元.
课后小练
课后小练
1.为了迎接十四运,提高智慧城市水平,西安公交公司近期推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,x表示活动推出的天数,y表示每天使用扫码支付的人次(单位:十人次),统计数据如表下所示:
x
1
2
3
4
5
6
7
y
6
11
21
34
66
101
196
根据以上数据,绘制了散点图.
(1)根据散点图判断,在推广期内, y=a+bx 与 y=c?dx ( c,?d 均为大于零的常数),哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由);
(2)根据(1)的判断结果及表1中的数据,建立y与x的回归方程,并预测活动推出第8天使用扫码支付的人次;
(3)推广期结束后,车队对乘客的支付方式进行统计,结果如下表:
支付方式
现金
乘车卡
扫码
比例
10%
60%
30%
西安公交六公司车队为缓解周边居民出行压力,以90万元的单价购进了一批新车,根据以往的经验可知,每辆车每个月的运营成本约为0.66万元.已知该线路公交车票价为2元,使用现金支付的乘客无优惠,使用乘车卡支付的乘客享受8折优惠,扫码支付的乘客随机优惠,根据统计结果得知,使用扫码支付的乘客中有 16 的概率享受7折优惠,有 13 的概率享受8折优惠,有 12 的概率享受9折优惠.预计该车队每辆车每个月有2万人次乘车,根据所给数据以事件发生的频率作为相应事件发生的概率,在不考虑其它因素的条件下,按照上述收费标准,请你估计这批车辆需要几年(结果取整数年)才能盈利?
参考数据:
y
v
i=17xiyi
i=17xivi
100.54
62.14
1.54
2535
50.12
3.47
其中其中 vi=lgyi , v=17i=17vi ,
参考公式:对于一组数据 (u1,?v1) , (u2,?v2) ,…, (un,?vn) ,其回归直线 v=α+βu 的斜率和截距的最小二乘估计公式分别为: β=i=1nuivi?nu?vi=1nui2?nu2 , α=v?βu .
2.某公司为一所山区小学安装了价值2万元的一台饮用水净化设备,每年都要为这台设备支出保养维修费用,我们称之为设备年度保养维修费.下表是该公司第 x 年为这台设备支出的年度保养维修费 y (单位:千元)的部分数据:
x
2
3
4
5
6
y
2.1
3.4
5.9
6.6
7.0
画出散点图如下:
通过计算得 y 与 x 的相关系数 r≈0.96 .由散点图和相关系数 r 的值可知, y 与 x 的线性相关程度很高.
附: b=i=1n(xi?x)(yi?y)i=1n(xi?x)2 , a=y?bx .
(1)建立 y 关于 x 的线性回归方程 y=bx+a ;
(2)若设备年度保养维修费不超过1.93万元就称该设备当年状态正常,根据(1)得到的线性回归方程,估计这台设备有多少年状态正常?
3.2021年2月25日,在全国脱贫攻坚总结表彰大会上,习近平总书记庄严宣告:我国脱贫攻坚战取得全面胜利.目前,陕西省56个贫困县已经全部脱贫摘帽,退出贫困县序列.2016年起,我省某贫困地区创新开展产业扶贫,响应第三产业的扶贫攻坚政策,经济收入逐年增加.该地的经济收入变化及构成比例如下表所示:
年份
2016年
2017年
2018年
2019年
2020年
年份代号 x
1
2
3
4
5
经济收人 y (单位:百万元)
5
8
13
18
20
2016年?2020年经济收入构成比例:
年份
类别
种植收人
养殖收人
第三产业收人
其他收人
2016年
60%
30%
6%
4%
2020年
34%
30%
30%
6%
参考公式:对于一组具有线性相关关系的数据 (xi,yi)(i=1,2,3,?,n) ,其回归直线 y=bx+a 的斜率和截距的最小二计分别为 b=i=1n(xi?x)(yi?y)i=1n(xi?x)2=i=1nxiyi?nxyi=1nxi2?nx2,a=y?bx
(1)根据上表,试分析:与2016年相比,2020年第三产业?种植业收入变化情况;
(2)求经济收入y关于x的线性回归方程,并预测2025年该地区的经济收入.
4.某公司研发了一种帮助家长解决孩子早教问题的萌宠机器人.萌宠机器人语音功能让它就像孩子的小伙伴一样和孩子交流,记忆功能还可以记住宝宝的使用习惯,很快找到宝宝想听的内容.同时提供快乐儿歌、国学经典、启蒙英语等早期教育内容,且云端内容可以持续更新.萌宠机器人一投放市场就受到了很多家长欢迎.为了更好地服务广大家长,该公司研究部门从流水线上随机抽取100件萌宠机器人(以下简称产品),统计其性能指数并绘制频率分布直方图(如图1):
产品的性能指数在 [50,70) 的适合托班幼儿使用(简称A类产品),在 [70,90) 的适合小班和中班幼儿使用(简称B类产品),在 [90,110] 的适合大班幼儿使用(简称C类产品),A,B,C,三类产品的销售利润分别为每件1.5,3.5,5.5(单位:元).以这100件产品的性能指数位于各区间的频率代替产品的性能指数位于该区间的概率.
参考公式:对于一组数据 (u1,υ1),(u2,υ2),?,(un,υn) ,其回归直线 υ=α+βu 的斜率和截距的最小二乘估计分别为 β=i=1n(ui?u)(υi?υ)i=1n(ui?u)2 , α=υ?βu .
(1)求每件产品的平均销售利润;
(2)该公司为了解年营销费用 x (单位:万元)对年销售量 y (单位:万件)的影响,对近5年的年营销费用 xi ,和年销售量 yi(i=1,2,3,4,5) 数据做了初步处理,得到的散点图(如图2)及一些统计量的值.
i=15ui
i=15υi
i=15(ui?u)(υi?υ)
i=15(ui?u)2
16.30
24.87
0.41
1.64
表中 ui=lnxi , υi=lnyi , u=15i=15ui , υ=15i=15υi .
根据散点图判断, y=a?xb 可以作为年销售量 y (万件)关于年营销费用 x (万元)的回归方程.
(i)建立 y 关于 x 的回归方程;
(ii)用所求的回归方程估计该公司应投入多少营销费,才能使得该产品一年的收益达到最大?
(收益=销售利润-营销费用,取 e4.159=64 ).
5.某地一公司的市场研究人员为了解公司生产的某产品的使用情况,从两个方面进行了调查统计,一是产品的质量参数x,二是产品的使用时间t(单位:千小时),经统计分析,质量参数x服从正态分布 N(0.8,0.0152) ,使用时间t与质量参数x之间有如下关系:
质量参数x
0.65
0.70
0.75
0.80
0.85
0.90
0.95
使用时间t
2.60
2.81
3.05
3.10
3.25
3.35
3.54
附:参考数据: x=0.8,t=3.1,i=17xi2=4.55,i=17ti2=67.88,0.115=0.339 .若 ξ?N(μ,σ2) ,则 P(μ?σ<ξ≤μ+σ)=0.6828,P(μ?2σ<ξ≤μ+2σ)=0.9544
参考公式:相关系数 r=i=1n(xi?x)(ti?t)i=1n(xi?x)2i=1n(ti?t)2 ;
回归直线方程为 t=bx+a ,其中 b=i=1n(xi?x)(ti?t)i=1n(xi?x)2,a=y?bx .
(1)该地监管部门对该公司的该产品进行检查,要求质量参数在0.785以上的产品为合格产品.现抽取20件该产品进行校验,求合格产品的件数的数学期望;
(2)该公司研究人员根据最小二乘法求得线性回归方程为 t=2.92x+0.76 ,请用相关系数说明使用时间t与质量参数x之间的关系是否可用线性回归模型拟合.
答案解析
【答案】
(1)根据散点图判断,在推广期内, y=c?dx ( c,?d 均为大于零的常数),适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型;
(2)根据(1)的判断结果 y=c?dx ,两边取对数得: lgy=lgc+lgd?x ,
其中 vi=lgyi , v=17i=17vi=1.54 , i=17xivi=50.12 , x=4 , i=17xi2=140 ,
∴β=lgd=i=17xivi?nx?vi=1nxi2?nx2=0.25 , α=lgc=v?βx=0.54 ,
∴lgy=0.54+0.25x , ∴y=100.54+0.25?x=3.47×100.25x .
当 x=8 时, y=100.54+0.25?8=3.47×102=347 ,
∴活动推出第8天使用扫码支付的人次为3470人;
(3)设一名乘客一次乘车的费用为 ξ 元,
由题意知: ξ 所有可能取值为:1.4,1.6,1.8,2,
∴P(ξ=1.4)=0.3×16=0.05 , P(ξ=1.6)=0.6+0.3×13=0.7 , P(ξ=1.8)=0.3×12=0.15 , P(ξ=2)=0.1 ,
∴E(ξ)=1.4×0.05+1.6×0.7+1.8×0.15+2×0.1=1.66 ,
假设这批车需要 n(n∈N?) 年才能开始盈利,则 1.66×2×12×n≥90+0.66×12×n ,
解得: n≥2.82 ,∴需要3年才能盈利.
【解析】
(1)根据散点图知 y=c?dx适宜作 y与x 的回归方程类型;
(2)对 y=c?dx两边同时取常用对数,化为线性回归方程,求出对应的系数,写出 y与x 的回归方程,再利用方程求出x=8时对应的函数值.
2.【答案】
(1)解: x=15×(2+3+4+5+6)=4 ,
y=15×(2.1+3.4+5.9+6.6+7)=5 .
b=i=15(xi?x)(yi?y)i=15(xi?x)2=1310=1.3 .
∴a=y?bx=5?1.3×4=?0.2 .
∴ 线性回归方程为 y=1.3x?0.2 .
(2)解:设这台设备有 x 年状态正常,由已知得 y≤19.3 ,即 1.3x?0.2≤19.3 .
解 1.3x?0.2≤19.3 得 x≤15 .
∴ 估计该设备有 15 年状态正常
【解析】
(1)根据已知条件求出x=15×(2+3+4+5+6)=4y=15×(2.1+3.4+5.9+6.6+7)=5 , 再根据公式可求出 ?b^,a^即可得出 ?y?关于?x?的线性回归方程;?
(2) 设这台设备有?x?年状态正常,由已知得?y≤19.3?,即?1.3x?0.2≤19.3?解不等式即可得出。
3.【答案】 (1)解:①与2016年相比,2020年第三产业的收入占比大幅度增加;2016年第三产业的收入为0.3百万元,2020年第三产业的收入为6百万元,收入大幅度增加;
②与2016年相比,种植业收入占比减少,但种植业收入依然保持增长;
(2)解: x=1+2+3+4+55=3,y=5+8+13+18+205=12.8
i=15xi2=12+22+32+42+52=55,i=15xiyi=1×5+2×8+3×13+4×18+5×20=232 b∧=i=15xiyi?5xyi=15xi2?5x2=232?5×3×12.855?5×3×3=4
∴a=y?bx=12.8?4×3=0.8
故经济收入 y 关于 x 的线性回归方程为 y=0.8+4x.
当 x=10 时, y=40.8 ,则2025年该地区的经济收入预测为40.8百万元.
【解析】
直接由表格中数据分析与2016 年相比, 2020年第三产业、种植业收入变化情况即可。
(2) 由已知数据求得 a^与b^的值 可得线性回归方程,取 x=10 求得 y^ 可得2025年该地区的经济收入.
4.【答案】
(1)解:设每件产品的销售利润为 ξ 元,则 ξ 的所有可能取值为1.5,3.5,5.5,
由直方图可得, A , B , C 三类产品的频率分别为0.15、0.45、0.4,
所以, P(ξ=1.5)=0.15 , P(ξ=3.5)=0.45 , P(ξ=5.5)=0.4 ,
所以随机变量 ξ 的分布列为:
ξ
1.5
3.5
5.5
P
0.15
0.45
0.4
所以, Eξ=1.5×0.15+3.5×0.45+5.5×0.4=4 ,
故每件产品的平均销售利润为4元;
(2)解:(i)由 y=a?xb 得, lny=ln(a?xb)=lna+blnx ,
令 u=lnx , υ=lny , c=lna ,则 υ=c+bu ,
由表中数据可得, b=i=15(ui?u)(υi?υ)i=15(ui?u)2=0.411.61=0.25 ,
则 c=υ?bu=24.875?0.25×16.305=4.159 ,
所以, υ=4.159+0.25u ,
即 lny=4.159+0.25lnx=ln(e4.159?x14) ,
因为 e4.159=64 ,所以 y=64x14 ,
故所求的回归方程为 y=64x14 ;
(ii)设年收益为 z 万元,则 z=(Eξ)?y?x=256x14?x ,
设 t=x14 , f(t)=256t?t4 ,
则 f'(t)=256?4t3=4(64?t3) ,
当 t∈(0,4) 时, f'(t)>0 , f(t) 在 (0,4) 单调递增,
当 t∈(4,+∞) 时, f'(t)<0 , f(t) 在 (4,+∞) 单调递减,
所以,当 t=4 ,即 x=256 时, z 有最大值为768,
即该厂应投入256万元营销费,能使得该产品一年的收益达到最大768万元.
【解析】
(1)设每件产品的销售利润为ξ元,则ξ的所有可能取值为1.5,3.5,5.5,求出概率,得到分布列,然后求解期望;
(2)(i)由y=a?xb得,lny=ln(a?xb)=lna+blnx,令u=lnx,υ=lny,c=lna,可得υ=c+bu,求出回归直线方程的系数,然后求解y关于x的回归方程;
(ii)设年收益为z万元,则 z=(Eξ)?y?x=256x14?x?, 利用换元法,以及函数的导数,判断函数的单调性,求解函数的最值,推出结果.
5.【答案】
(1)解:一件产品的质量参数在0.785以上的概率 p=1?1?0.68282=0.8414 ,
设抽取20件该产品中为合格产品的件数为 ξ ,则 ξ~B(20?,?0.8414) ,
则 E(ξ)=20×0.8414=16.828 .
(2)解: i=1n(xi?x)2=i=1nxi2?2xi=1nxi+nx2=i=1nxi2?2x?nx+nx2=i=1nxi2?nx2 ,
同理, i=1n(ti?t)2==i=1nti2?nt2 ,
∵b=i=1n(xi?x)(ti?t)i=1n(xi?x)2 , ∴i=1n(xi?x)(ti?t)=bi=1n(xi?x)2 ,
∴r=i=1n(xi?x)(ti?t)i=1n(xi?x)2(ti?t)2=bi=1n(xi?x)2i=1n(xi?x)2(ti?t)2=bi=1n(xi?x)2i=1n(ti?t)2
=bi=1nxi2?nx2i=1nti2?nt2=2.92×4.55?7×0.8267.88?7×3.12=2.92×0.070.61
=2.92×0.114=2.92×0.337≈0.98
所以使用时间 t 与质量参数 x 之间具有较强的线性相关关系,可用线性回归模型拟合.
【解析】
(1)根据题意由概率的定义结合已知条件求出结果,再由正太分布的数值结合期望公式计算出答案即可。
(2)结合已知条件把数值代入到公式计算出参考数据,由此得到线性回归方程并代入数值计算出 使用时间 t 与质量参数 x 之间具有较强的线性相关关系,可用线性回归模型拟合.
