8.3 列联表与独立性检验 讲义-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(Word含答案)
文档属性
| 名称 | 8.3 列联表与独立性检验 讲义-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(Word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 330.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 17:27:22 | ||
图片预览




文档简介
第八章 成对数据的统计分析
第八章 成对数据的统计分析
8.3列联表与独立性检验
8.3列联表与独立性检验
知识梳理
知识梳理
知识点1.分类变量与列联表
分类变量
为了方便,会使用一种特殊的随机变量,区别不同的现象或性质,这随机变量称为分类变量.分类变量的取值可以用实数表示.
列联表
(1).2×2列联表给出了成对分类变量数据的交叉分类频数.
(2).定义一对分类变量X和Y,我们整理数据如下表所示:
X
Y
合计
Y=0
Y=1
X=0
a
b
a+b
X=1
c
d
c+d
合计
a+c
b+d
n=a+b+c+d
像这种形式的数据统计表称为2×2列联表.
3.两个分类变量之间关联关系的定性分析方法
(1)频率分析法:通过对样本的分类变量的不同类别事件发生的频率大小进行分析分类变量之间是否有关联关系.通常通过列联表列出两个分类变量的频数表来进行分析.
(2)图形分析法:与表格相比,图形更能直观地反映两个分类变量间是否互相影响,常用等高堆积条形图展示列联表数据的频率特征.
知识点2.独立性检验
1.定义:利用χ2的取值推断分类变量X和Y是否独立的方法称为χ2独立性检验,读作“卡方独立性检验”.简称独立性检验.
2.χ2=,其中n=a+b+c+d.
3.独立性检验解决实际问题的主要环节
(1)提出零假设H0:X和Y相互独立,并给出在问题中的解释.
(2)根据抽样数据整理出2×2列联表,计算χ2的值,并与临界值xα比较.
(3)根据检验规则得出推断结论.
(4)在X和Y不独立的情况下,根据需要,通过比较相应的频率,分析X和Y间的影响规律.
题型探究
题型探究
例1.为了解国内不同年龄段的民众旅游消费基本情况,某旅游网站从其数据库中随机抽取了100条客户信息进行分析,这些客户一年的旅游消费金额如下表:
旅游消费(千元)
false
false
false
false
false
false
合计
年轻人(人)
9
10
9
7
3
2
40
中老年(人)
5
9
13
13
11
9
60
(1)分别估计年轻人和中老年人的旅游消费的平均数(同一组中的数据用该组区间的中点值作代表)(精确到0.01);
(2)把一年旅游消费金额满8千元的称为“高消费”,否则称为“低消费”.
(i)从这些“低消费”客户中随机选一人,估计该客户是年轻人的概率;
(ii)完成false列联表,并判断能否有97.5%的把握认为旅游消费高低与年龄有关.
低消费
高消费
合计
年轻人(人)
中老年(人)
合计
参考公式:false,其中false.
附临界值表:
false
0.100
0.050
0.025
0.010
0.001
false
2.706
3.841
5.024
6.635
10.828
【答案】(1)年轻人旅游消费的平均数为:false(千元),中老年人旅游消费的平均数为:false(千元);(2)(i)false;(ii)列联表答案见解析,有97.5%的把握认为旅游消费高低与年龄有关.
【详解】
解:(1)由表格可知,年轻人旅游消费的平均数为:
false(千元).
中老年人旅游消费的平均数为:
false(千元).
(2)(i)由表格可知,样本中“低消费”总客户数为false,
其中“低消费”的年轻人有false人.
所以随机选一人该客户是年轻人的概率为false.
(ii)false列联表如下:
低消费
高消费
合计
年轻人(人)
35
5
40
中老年(人)
40
20
60
合计
75
25
100
因为false,
所以有97.5%的把握认为旅游消费高低与年龄有关.
例2.高考在即,进行适量的体育锻炼有助于缓解考试压力,为了解高三年级同学们每天放学后主动参加体育锻炼的情况,随机调查了false名高三学生,通过调查把这false人每天锻炼的时间(单位:分钟)绘制成频数分布表,如下表所示:
锻炼时间
false
false
false
false
false
false
人数
false
false
false
false
false
false
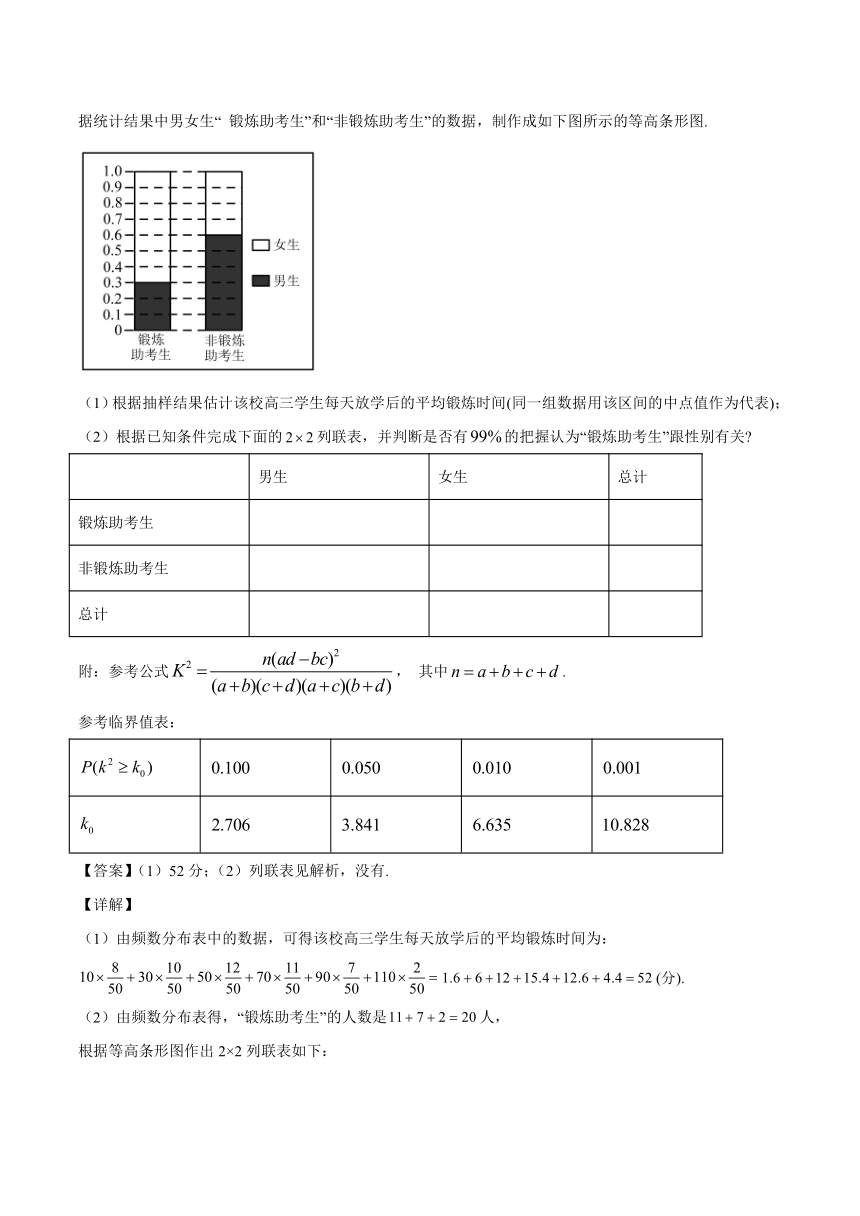
若把每天锻炼时间在false分钟以上(含false分钟)的同学称为“ 锻炼助考生”,余下的称为“非锻炼助考生”,根据统计结果中男女生“ 锻炼助考生”和“非锻炼助考生”的数据,制作成如下图所示的等高条形图.
(1)根据抽样结果估计该校高三学生每天放学后的平均锻炼时间(同一组数据用该区间的中点值作为代表);
(2)根据已知条件完成下面的false列联表,并判断是否有false的把握认为“锻炼助考生”跟性别有关?
男生
女生
总计
锻炼助考生
非锻炼助考生
总计
附:参考公式false, 其中false.
参考临界值表:
false
false
false
false
false
false
false
false
false
false
【答案】(1)52分;(2)列联表见解析,没有.
【详解】
(1)由频数分布表中的数据,可得该校高三学生每天放学后的平均锻炼时间为:
falsefalse(分).
(2)由频数分布表得,“锻炼助考生”的人数是false人,
根据等高条形图作出2×2列联表如下:
男生
女生
总计
锻炼助考生
false
false
false
非锻炼助考生
false
false
false
总计
false
false
false
可得false,
所以没有false的把握认为“锻炼助考生”跟性别有关.
例3.目前,我国大学生、白领和工薪阶层是网购人数最多的群体,一项调查显示女性网民成为网络购物的活跃人群,网购用户年龄大多集中在18~35岁,月收入集中在1500~3500元网购大额产品的用户中,男性多于女性;收入更高的用户,网购金额和频率更高;35~45岁的网民,在各年龄段的用户中网络购物频率和金额最高.若全年网购超过40次定义为热衷于网购,现对某市网民进行“热衷网购与性别分布”的调查,采用随机抽样的方法抽取一个容量为200的样本,其中热衷网购的占比false.
(Ⅰ)请根据图表中的数据,完成false联表,并根据列联表判断是否有99.9%的把握认为热衷于网购与性别有关?
热衷网购
非热衷网购
总计
女性
120
男性
30
总计
200
(Ⅱ)若在热衷网购网民中按照分层抽样的方法抽取的5名网民,再从中随机抽取2名网民,求这2人中恰有1人为男性的概率.
参考公式:false,false.
附表:
false
0.100
0.050
0.010
0.005
0.001
false
2.706
3.841
6.635
7.879
10.828
【答案】(Ⅰ)列联表见解析,有99.9%的把握认为热衷网购与性别有关;(Ⅱ)false.
【详解】
(Ⅰ)依题意抽取一个容量为200的样本,其中热衷网购的占比false,故热衷网购的总人数为150人,补充完整的false列联表如表所示:
热衷网购
非热衷网购
总计
女性
120
20
140
男性
30
30
60
总计
150
50
200
false,故有99.9%的把握认为热衷网购与性别有关.
(Ⅱ)在热衷网购网民中按照分层抽样的方法抽取的5名网民,其中女性为4人,男性为1人,设4名女性网民分别为false,false,false,false,1名男性网民为false,从5人中随机抽取2人,则有false,false,false,false,false,false,false,false,false,false,共10种基本事件.
这2人中恰有1人为男性的基本事件为false,false,false,false,共4种情况,
故抽取5名网民,再从中随机抽取2名网民恰有1人为男性的概率false.
例4.2020年3月,工业和信息化部信息通信发展司发布《工业和信息化部关于推动5G加快发展的通知》鼓励基础电信企业通过套餐升级优惠?信用购机等举措,促进5G终端消费,加快用户向5G迁移.为了落实通知要求,掌握用户升级迁移情况及电信企业服务措施,某市调研部门随机选取了甲?乙两个电信企业的用户共165户作为样本进行满意度调查,并针对企业服务措施设置了达标分数线,按照不低于80分的定为满意,低于80分的为不满意,调研人员制作了如图所示的false列联表.已知从样本的165户中随机抽取1户为满意的概率是false.
满意
不满意
合计
甲企业用户
75
乙企业用户
20
合计
(1)将false列联表补充完整,并判断能否有95%的把握认为“满意度与电信企业服务措施有关系”?
(2)视样本的频率为概率,在该市乙企业的所有用户中任取3户,记取出的3户中不满意的户数为false,求false的分布列和数学期望.
下面临界值表仅供参考:
false
0.15
0.10
0.05
0.025
0.010
0.005
0.001
false
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:false,其中false)
【答案】(1)列联表答案见解析,有95%的把握认为“满意度与电信企业服务措施有关系”;(2)分布列答案见解析,数学期望:false.
【详解】
(1)设样本中乙企业用户中满意的有false户,结合列联表知false,解得false,
所以,false列联表是:
满意
不满意
合计
甲企业用户
75
10
85
乙企业用户
60
20
80
合计
135
30
165
false
故可以判断有95%的把握认为“满意度与电信企业服务措施有关系”
(2)设“从样本中的乙企业用户中任取一户为不满意”为事件A,则false
由题意可知:false的可能值为0,1,2,3,false,
则false,false,
false,false
所以false的分布列为
false
0
1
2
3
false
false
false
false
false
从而false的数学期望为false.
例5.为了解小学生的体能情况,现抽取某小学六年级false名学生进行跳绳测试,观察记录学生们一分钟内的跳绳个数,将所得的数据整理后画出如图所示的频率分布直方图,跳绳个数落在区间false,false,false内的频数之比为false.若规定某学生一分钟内的跳绳个数大于或等于false个,则成绩优秀;否则,成绩为非优秀.
(1)求这些学生中成绩优秀的人数;
(2)已知这false名小学生中女生占false,且成绩优秀的女生有false人,请根据以上调查结果将下面的false列联表补充完整,并判断能否有false的把握认为成绩“优秀”与性别有关.
成绩“优秀”
成绩“非优秀”
总计
男生
女生
总计
附:false,false.
false
0.050
0.025
0.010
0.001
false
3.841
5.024
6.635
10.828
【答案】(1)false;(2)列联表见解析,没有false的把握认为成绩“优秀”与性别有关.
【详解】
(1)设区间false内的频率为false,则false,false内的频率分别为false和false,
false,解得:false.
false区间false和false内的频率为false和false,
false这些学生中成绩优秀的人数为false.
(2)由题意知:女生有false人,男生有false人,
可得false列联表如下:
成绩“优秀”
成绩“非优秀”
总计
男生
false
false
false
女生
false
false
false
总计
false
false
false
false,
false没有false的把握认为成绩“优秀”与性别有关.
课后小练
课后小练
1.某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12],试估计该校学生每周平均体育运动时间的平均数.
(3)已知在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成下面的列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间超过4小时与性别有关”.
附:K2= n(ad?bc)2(a+b)(c+d)(a+c)(b+d) .
每周平均体育运动时间超过4小时
每周平均体育运动时间不超过4小时
总计
男
女
60
总计
300
2.为进一步提升学生学习数学的热情,学校举行了数学学科知识竞赛.为了解学生对数学竞赛的喜爱程度是否与性别有关,对高中部200名学生进行了问卷调查,得到如下 2×2 列联表:
喜欢数学竞赛
不喜欢数学竞赛
合计
男生
70
女生
30
合计
已知在这200名学生中随机抽取1人,抽到喜欢数学竞赛的概率为0.6.
参考公式及数据: K2=n(ad?bc)2(a+b)(c+d)(a+c)(b+d)
P(K2≥k)
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.01
0.005
0.001
k
0.46
0.71
1.32
2.07
2.71
3.84
5.024
6.635
7.879
10.828
(1)将 2×2 列联表补充完整,并判断是否有90%的把握认为喜欢数学竞赛与性别有关?
(2)从上述不喜欢数学竞赛的学生中用分层抽样的方法抽取8名学生,再在这8人中抽取3人调查其喜欢的活动类型,用 X 表示3人中女生的人数,求 X 的分布列及数学期望.
3.新型冠状病毒的传染性是非常强的,而且可以通过接触传播或者是呼吸道飞沫传播,感染人群年龄大多数是40岁以上的人群.该病毒进入人体后有潜伏期,并且潜伏期越长,感染他人的可能性越高,现对100个病例的潜伏期(单位:天)进行调查,统计发现潜伏期中位数为5,平均数为7.21,方差为5.08.如果认为超过8天的潜伏期属于“长潜伏期”.按照年龄统计样本得到下面的列联表:
长潜伏期
非长潜伏期
40岁以上
15
55
40岁及以下
10
20
附: K2=n(ad?bc)2(a+b)(c+d)(a+c)(b+d) .
K2≥k
0.1
0.05
k
2.706
3.841
若随机变量 Z 服从正态分布 N(μ,σ2) ,则 P(μ?σ(1)能否有90%以上的把握认为“长潜伏期”与年龄有关;
(2)假设潜伏期 Z 服从正态分布 N(μ,σ2) ,其中 μ 近似为样本平均数, σ2 近似为样本方差,现在很多省份对入境旅客一律要求隔离14天,请用概率的知识解释其合理性;
(3)以题目中的样本频率估计概率,并计算4个病例中有 X(X∈N?) 个进入“长潜伏期”的期望与方差.
4.这一年来人类与新型冠状病毒的“战争”让人们逐渐明白一个道理,人类社会组织模式的差异只是小事情,病毒在地球上存在了三四十亿年,而人类的文明史不过只有几千年而已,人类无法消灭病毒,只能与之共存,或者病毒自然消亡,在病毒面前,个体自由要服从于集体或者群体生命的价值.在传染病学中,通常把从致病刺激物侵入机体内或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期,因此我们应该注意做好良好的防护措施和隔离措施.某研究团队统计了某地区10000名患者的相关信息,得到如表表格:
潜伏期(天)
(0,2]
(2,4]
(4,6]
(6,8]
(8,10]
(10,12]
(12,14]
人数
600
1900
3000
2500
1600
250
150
附: K2=n(ad?bc)2(a+b)(c+d)(a+c)(b+d) .
P(K2≥k0)
0.150
0.100
0.050
0.025
0.010
0.005
0.001
k0
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(1)新冠肺炎的潜伏期受诸多因素的影响,为研究潜伏期与年龄的关系,通过分层抽样从10000名患者中抽取200人进行研究,完成下面的2×2列联表,并判断能否在犯错误的概率不超过0.001的前提下认为潜伏期与患者年龄有关?
潜伏期 ≤8 天
潜伏期 >8 天
总计
60岁以上(含60岁)
150
60岁以下
30
总计
200
(2)依据上述数据,将频率作为概率,且每名患者的潜伏期是否超过8天相互独立.为了深入研究,该团队在这一地区抽取了20名患者,其中潜伏期不超过8天的人数最有可能是多少?
5.在新冠肺炎疫情得到有效控制后,某公司迅速复工复产,为扩大销售额,提升产品品质,现随机选取了100名顾客到公司体验产品,并对体验的满意度进行评分(满分100分).体验结束后,该公司将评分制作成如图所示的直方图.
(1)将评分低于80分的为“良”,80分及以上的为“优”.根据已知条件完成下面 2×2 列联表,能否在犯错误的概率不超过0.10的前提下认为体验评分为“优良”与性别有关.
良
优
合计
男
40
女
40
合计
(2)为答谢顾客参与产品体验活动,在体验度评分为 [50,60) 和 [90,100] 的顾客中用分层抽样的方法选取了6名顾客发放优惠卡.若在这6名顾客中,随机选取4名再发放纪念品,记体验评分为 [50,60) 的顾客获得纪念品数为随机变量 X ,求 X 的分布列和数学期望.
附表及公式: K2=n(ad?bc)2(a+b)(c+d)(a+c)(b+d)
P(K2≥k0)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.072
2.076
3.841
5.024
6.635
7.879
10.828
答案解析
1.【答案】 (1)解: 300×450015000=90
∴应收集90位女生的样本数据;
(2)解: (1×0.025+3×0.100+5×0.150+7×0.125+9×0.075+11×0.025)×2=5.8
∴该校学生每周平均体育运动时间的平均数约为5.8小时;
(3)解:
每周平均体育运动时间超过4小时
每周平均体育运动时间不超过4小时
总计
男
165
45
210
女
60
30
90
总计
225
75
300
∴ K2=300×(45×60?165×30)2210×90×75×225≈4.762>3.841
∴有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
【解析】
(1)根据分层抽样的定义直接求解即可;
(2)根据直方图,利用公式x=x1p1+x2p2+??+xnpn直接求解即可;
(3)根据独立性检验公式直接求解即可.
2.【答案】
(1)解:由200名学生中抽取一人抽到喜欢数学竞赛的概率为0.6,可得喜欢数学竞赛的总人数为 200×0.6=120 ,
所以
喜欢数学竞赛
不喜欢数学竞赛
合计
男生
70
50
120
女生
50
30
80
合计
120
80
200
∴k2=200×(70×30?50×50)2120×120×80×80≈0.35<2.71 ,
∴ 没有90%的把握认为喜欢数学竞赛与性别有关;
(2)解:由题意可知抽取不喜欢数学竞赛的男生有5人,女生有3人,
∴X 的可能取值为0,1,2,3,
P(X=0)=C53C83=1056=528 ;
P(X=1)=C52C31C83=3056=1528 ;
P(X=2)=C51C32C83=1556 ;
P(X=3)=C33C83=156 ;
所以X的分布列为:
X
0
1
2
3
P
528
1528
1556
156
E(X)=0×528+1×1528+2×1556+3×156=98 .
【解析】
(1)利用已知条件补充完整 2×2 列联表,再利用独立性检验的方法判断出没有90%的把握认为喜欢数学竞赛与性别有关。
(2)利用已知条件求出随机变量X可能的取值,再利用组合数公式结合古典概型求概率公式,进而求出随机变量X的分布列,再利用随机变量X的分布列结合数学期望公式,进而求出随机变量X的数学期望。
3.【答案】
(1)解: K2=n(ad?bc)2(a+b)(c+d)(a+c)(b+d)=100×(15×20?55×10)270×30×25×75≈1.587 ,
由于 1.587<2.706 ,
故没有90%以上的把握认为“长潜伏期”与年龄有关;
(2)解:若潜伏期 Z?N(7.21,2.252) ,
此时 μ+3σ=7.21+3×2.25=13.96 ,
由 P(Z≥13.96)=1?0.99742=0.0013 ,
显然潜伏期超过14天的概率很低,
因此隔离14天是合理的.
(3)解:由于100个病例中有25个属于长潜伏期,
若以样本频率估计概率,英特患者属于“长潜伏期”的概率是 14 ,
因为 X~B(4,14) ,
所以期望 E(X)=np=4×14=1 ;
方差 D(X)=np(1?p)=4×14×34=34 .
【解析】
(1)利用已知条件结合独立性检验的方法,进而判断出没有90%以上的把握认为“长潜伏期”与年龄有关。
(2)利用潜伏期 Z 服从正态分布 N(μ,σ2) , 再结合正态分布对应的函数的图象的对称性,再利用已知条件求出 P(Z≥13.96)=0.0013 ,显然潜伏期超过14天的概率很低,因此隔离14天是合理的。
(3) 以样本频率估计概率结合频率等于频数除以样本容量的公式,再结合已知条件得出英特患者属于“长潜伏期”的概率是 14 , 再利用随机变量X服从二项分布,再结合二项分布求数学期望公式和方差公式,进而求出4个病例中有 X(X∈N?) 个进入“长潜伏期”的期望与方差。?
4.【答案】
(1)解:由表中数据可知,潜伏期大于8天的人数为 1600+250+15010000×200=40 人,
补充完整的2×2列联表如下,
潜伏期 ≤8 天
潜伏期 >8 天
总计
60岁以上(含60岁)
130
20
150
60岁以下
30
20
50
总计
160
40
200
所以 K2=200×(130×20?30×20)2150×50×160×40≈16.667>10.828 ,
故能在犯错误的概率不超过0.001的前提下认为潜伏期与患者年龄有关.
(2)解:该地区10000名患者中潜伏期不超过8天的人数为 600+1900+3000+2500=8000 名,
将频率视为概率,潜伏期不超过8天的概率为 800010000=45 ,
所以抽取的20名患者中潜伏期不超过8天的人数最有可能是 20×45=16 名
【解析】
(1)先计算潜伏期大于8天的人数,完成2×2列联表,再计算K的观测值K2 , 并与附表中的数据对比,即可作出判断;
(2)将频率作为概率,计算该地区10000名患者中潜伏期不超过8天的概率,即可得解.
5.【答案】
(1)解:根据题意,评分低于80分的有 (0.01+0.01+0.02)×10×100=40 人,即评分为“良”的有 40 人,所以列联表如下:
良
优
合计
男
20
20
40
女
20
40
60
合计
40
60
100
由题得, K2=100(20×40?20×20)240×60×60×40=259≈2.78>2.706
所以,能在犯错误的概率不超过0.10的前提下认为体验评分为“优良”与性别有关.
(2)解:由已知得体验度评分为 [50,60) 和 [90,100] 的顾客分别有10人,20人,则在随机抽取的6人中评分为 [50,60) 有2人,评分为 [90,100] 有4人.
则 X 可能的取值有0,1,2.
P(X=0)=C44C64=115 , P(X=1)=C21?C43C64=815 , P(X=2)=C22?C42C64=615 ,
则 X 的分布列为
X
0
1
2
P
115
815
615
所以, E(X)=0×115+1×815+2×615=43 .
【解析】
(1)根据题意填写列联表,计算K2 , 对照附表得出结论;
(2)利用分层抽样法与列举法求出基本事件数,计算所求的概率值.
第八章 成对数据的统计分析
8.3列联表与独立性检验
8.3列联表与独立性检验
知识梳理
知识梳理
知识点1.分类变量与列联表
分类变量
为了方便,会使用一种特殊的随机变量,区别不同的现象或性质,这随机变量称为分类变量.分类变量的取值可以用实数表示.
列联表
(1).2×2列联表给出了成对分类变量数据的交叉分类频数.
(2).定义一对分类变量X和Y,我们整理数据如下表所示:
X
Y
合计
Y=0
Y=1
X=0
a
b
a+b
X=1
c
d
c+d
合计
a+c
b+d
n=a+b+c+d
像这种形式的数据统计表称为2×2列联表.
3.两个分类变量之间关联关系的定性分析方法
(1)频率分析法:通过对样本的分类变量的不同类别事件发生的频率大小进行分析分类变量之间是否有关联关系.通常通过列联表列出两个分类变量的频数表来进行分析.
(2)图形分析法:与表格相比,图形更能直观地反映两个分类变量间是否互相影响,常用等高堆积条形图展示列联表数据的频率特征.
知识点2.独立性检验
1.定义:利用χ2的取值推断分类变量X和Y是否独立的方法称为χ2独立性检验,读作“卡方独立性检验”.简称独立性检验.
2.χ2=,其中n=a+b+c+d.
3.独立性检验解决实际问题的主要环节
(1)提出零假设H0:X和Y相互独立,并给出在问题中的解释.
(2)根据抽样数据整理出2×2列联表,计算χ2的值,并与临界值xα比较.
(3)根据检验规则得出推断结论.
(4)在X和Y不独立的情况下,根据需要,通过比较相应的频率,分析X和Y间的影响规律.
题型探究
题型探究
例1.为了解国内不同年龄段的民众旅游消费基本情况,某旅游网站从其数据库中随机抽取了100条客户信息进行分析,这些客户一年的旅游消费金额如下表:
旅游消费(千元)
false
false
false
false
false
false
合计
年轻人(人)
9
10
9
7
3
2
40
中老年(人)
5
9
13
13
11
9
60
(1)分别估计年轻人和中老年人的旅游消费的平均数(同一组中的数据用该组区间的中点值作代表)(精确到0.01);
(2)把一年旅游消费金额满8千元的称为“高消费”,否则称为“低消费”.
(i)从这些“低消费”客户中随机选一人,估计该客户是年轻人的概率;
(ii)完成false列联表,并判断能否有97.5%的把握认为旅游消费高低与年龄有关.
低消费
高消费
合计
年轻人(人)
中老年(人)
合计
参考公式:false,其中false.
附临界值表:
false
0.100
0.050
0.025
0.010
0.001
false
2.706
3.841
5.024
6.635
10.828
【答案】(1)年轻人旅游消费的平均数为:false(千元),中老年人旅游消费的平均数为:false(千元);(2)(i)false;(ii)列联表答案见解析,有97.5%的把握认为旅游消费高低与年龄有关.
【详解】
解:(1)由表格可知,年轻人旅游消费的平均数为:
false(千元).
中老年人旅游消费的平均数为:
false(千元).
(2)(i)由表格可知,样本中“低消费”总客户数为false,
其中“低消费”的年轻人有false人.
所以随机选一人该客户是年轻人的概率为false.
(ii)false列联表如下:
低消费
高消费
合计
年轻人(人)
35
5
40
中老年(人)
40
20
60
合计
75
25
100
因为false,
所以有97.5%的把握认为旅游消费高低与年龄有关.
例2.高考在即,进行适量的体育锻炼有助于缓解考试压力,为了解高三年级同学们每天放学后主动参加体育锻炼的情况,随机调查了false名高三学生,通过调查把这false人每天锻炼的时间(单位:分钟)绘制成频数分布表,如下表所示:
锻炼时间
false
false
false
false
false
false
人数
false
false
false
false
false
false
若把每天锻炼时间在false分钟以上(含false分钟)的同学称为“ 锻炼助考生”,余下的称为“非锻炼助考生”,根据统计结果中男女生“ 锻炼助考生”和“非锻炼助考生”的数据,制作成如下图所示的等高条形图.
(1)根据抽样结果估计该校高三学生每天放学后的平均锻炼时间(同一组数据用该区间的中点值作为代表);
(2)根据已知条件完成下面的false列联表,并判断是否有false的把握认为“锻炼助考生”跟性别有关?
男生
女生
总计
锻炼助考生
非锻炼助考生
总计
附:参考公式false, 其中false.
参考临界值表:
false
false
false
false
false
false
false
false
false
false
【答案】(1)52分;(2)列联表见解析,没有.
【详解】
(1)由频数分布表中的数据,可得该校高三学生每天放学后的平均锻炼时间为:
falsefalse(分).
(2)由频数分布表得,“锻炼助考生”的人数是false人,
根据等高条形图作出2×2列联表如下:
男生
女生
总计
锻炼助考生
false
false
false
非锻炼助考生
false
false
false
总计
false
false
false
可得false,
所以没有false的把握认为“锻炼助考生”跟性别有关.
例3.目前,我国大学生、白领和工薪阶层是网购人数最多的群体,一项调查显示女性网民成为网络购物的活跃人群,网购用户年龄大多集中在18~35岁,月收入集中在1500~3500元网购大额产品的用户中,男性多于女性;收入更高的用户,网购金额和频率更高;35~45岁的网民,在各年龄段的用户中网络购物频率和金额最高.若全年网购超过40次定义为热衷于网购,现对某市网民进行“热衷网购与性别分布”的调查,采用随机抽样的方法抽取一个容量为200的样本,其中热衷网购的占比false.
(Ⅰ)请根据图表中的数据,完成false联表,并根据列联表判断是否有99.9%的把握认为热衷于网购与性别有关?
热衷网购
非热衷网购
总计
女性
120
男性
30
总计
200
(Ⅱ)若在热衷网购网民中按照分层抽样的方法抽取的5名网民,再从中随机抽取2名网民,求这2人中恰有1人为男性的概率.
参考公式:false,false.
附表:
false
0.100
0.050
0.010
0.005
0.001
false
2.706
3.841
6.635
7.879
10.828
【答案】(Ⅰ)列联表见解析,有99.9%的把握认为热衷网购与性别有关;(Ⅱ)false.
【详解】
(Ⅰ)依题意抽取一个容量为200的样本,其中热衷网购的占比false,故热衷网购的总人数为150人,补充完整的false列联表如表所示:
热衷网购
非热衷网购
总计
女性
120
20
140
男性
30
30
60
总计
150
50
200
false,故有99.9%的把握认为热衷网购与性别有关.
(Ⅱ)在热衷网购网民中按照分层抽样的方法抽取的5名网民,其中女性为4人,男性为1人,设4名女性网民分别为false,false,false,false,1名男性网民为false,从5人中随机抽取2人,则有false,false,false,false,false,false,false,false,false,false,共10种基本事件.
这2人中恰有1人为男性的基本事件为false,false,false,false,共4种情况,
故抽取5名网民,再从中随机抽取2名网民恰有1人为男性的概率false.
例4.2020年3月,工业和信息化部信息通信发展司发布《工业和信息化部关于推动5G加快发展的通知》鼓励基础电信企业通过套餐升级优惠?信用购机等举措,促进5G终端消费,加快用户向5G迁移.为了落实通知要求,掌握用户升级迁移情况及电信企业服务措施,某市调研部门随机选取了甲?乙两个电信企业的用户共165户作为样本进行满意度调查,并针对企业服务措施设置了达标分数线,按照不低于80分的定为满意,低于80分的为不满意,调研人员制作了如图所示的false列联表.已知从样本的165户中随机抽取1户为满意的概率是false.
满意
不满意
合计
甲企业用户
75
乙企业用户
20
合计
(1)将false列联表补充完整,并判断能否有95%的把握认为“满意度与电信企业服务措施有关系”?
(2)视样本的频率为概率,在该市乙企业的所有用户中任取3户,记取出的3户中不满意的户数为false,求false的分布列和数学期望.
下面临界值表仅供参考:
false
0.15
0.10
0.05
0.025
0.010
0.005
0.001
false
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:false,其中false)
【答案】(1)列联表答案见解析,有95%的把握认为“满意度与电信企业服务措施有关系”;(2)分布列答案见解析,数学期望:false.
【详解】
(1)设样本中乙企业用户中满意的有false户,结合列联表知false,解得false,
所以,false列联表是:
满意
不满意
合计
甲企业用户
75
10
85
乙企业用户
60
20
80
合计
135
30
165
false
故可以判断有95%的把握认为“满意度与电信企业服务措施有关系”
(2)设“从样本中的乙企业用户中任取一户为不满意”为事件A,则false
由题意可知:false的可能值为0,1,2,3,false,
则false,false,
false,false
所以false的分布列为
false
0
1
2
3
false
false
false
false
false
从而false的数学期望为false.
例5.为了解小学生的体能情况,现抽取某小学六年级false名学生进行跳绳测试,观察记录学生们一分钟内的跳绳个数,将所得的数据整理后画出如图所示的频率分布直方图,跳绳个数落在区间false,false,false内的频数之比为false.若规定某学生一分钟内的跳绳个数大于或等于false个,则成绩优秀;否则,成绩为非优秀.
(1)求这些学生中成绩优秀的人数;
(2)已知这false名小学生中女生占false,且成绩优秀的女生有false人,请根据以上调查结果将下面的false列联表补充完整,并判断能否有false的把握认为成绩“优秀”与性别有关.
成绩“优秀”
成绩“非优秀”
总计
男生
女生
总计
附:false,false.
false
0.050
0.025
0.010
0.001
false
3.841
5.024
6.635
10.828
【答案】(1)false;(2)列联表见解析,没有false的把握认为成绩“优秀”与性别有关.
【详解】
(1)设区间false内的频率为false,则false,false内的频率分别为false和false,
false,解得:false.
false区间false和false内的频率为false和false,
false这些学生中成绩优秀的人数为false.
(2)由题意知:女生有false人,男生有false人,
可得false列联表如下:
成绩“优秀”
成绩“非优秀”
总计
男生
false
false
false
女生
false
false
false
总计
false
false
false
false,
false没有false的把握认为成绩“优秀”与性别有关.
课后小练
课后小练
1.某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12],试估计该校学生每周平均体育运动时间的平均数.
(3)已知在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成下面的列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间超过4小时与性别有关”.
附:K2= n(ad?bc)2(a+b)(c+d)(a+c)(b+d) .
每周平均体育运动时间超过4小时
每周平均体育运动时间不超过4小时
总计
男
女
60
总计
300
2.为进一步提升学生学习数学的热情,学校举行了数学学科知识竞赛.为了解学生对数学竞赛的喜爱程度是否与性别有关,对高中部200名学生进行了问卷调查,得到如下 2×2 列联表:
喜欢数学竞赛
不喜欢数学竞赛
合计
男生
70
女生
30
合计
已知在这200名学生中随机抽取1人,抽到喜欢数学竞赛的概率为0.6.
参考公式及数据: K2=n(ad?bc)2(a+b)(c+d)(a+c)(b+d)
P(K2≥k)
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.01
0.005
0.001
k
0.46
0.71
1.32
2.07
2.71
3.84
5.024
6.635
7.879
10.828
(1)将 2×2 列联表补充完整,并判断是否有90%的把握认为喜欢数学竞赛与性别有关?
(2)从上述不喜欢数学竞赛的学生中用分层抽样的方法抽取8名学生,再在这8人中抽取3人调查其喜欢的活动类型,用 X 表示3人中女生的人数,求 X 的分布列及数学期望.
3.新型冠状病毒的传染性是非常强的,而且可以通过接触传播或者是呼吸道飞沫传播,感染人群年龄大多数是40岁以上的人群.该病毒进入人体后有潜伏期,并且潜伏期越长,感染他人的可能性越高,现对100个病例的潜伏期(单位:天)进行调查,统计发现潜伏期中位数为5,平均数为7.21,方差为5.08.如果认为超过8天的潜伏期属于“长潜伏期”.按照年龄统计样本得到下面的列联表:
长潜伏期
非长潜伏期
40岁以上
15
55
40岁及以下
10
20
附: K2=n(ad?bc)2(a+b)(c+d)(a+c)(b+d) .
K2≥k
0.1
0.05
k
2.706
3.841
若随机变量 Z 服从正态分布 N(μ,σ2) ,则 P(μ?σ
(2)假设潜伏期 Z 服从正态分布 N(μ,σ2) ,其中 μ 近似为样本平均数, σ2 近似为样本方差,现在很多省份对入境旅客一律要求隔离14天,请用概率的知识解释其合理性;
(3)以题目中的样本频率估计概率,并计算4个病例中有 X(X∈N?) 个进入“长潜伏期”的期望与方差.
4.这一年来人类与新型冠状病毒的“战争”让人们逐渐明白一个道理,人类社会组织模式的差异只是小事情,病毒在地球上存在了三四十亿年,而人类的文明史不过只有几千年而已,人类无法消灭病毒,只能与之共存,或者病毒自然消亡,在病毒面前,个体自由要服从于集体或者群体生命的价值.在传染病学中,通常把从致病刺激物侵入机体内或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期,因此我们应该注意做好良好的防护措施和隔离措施.某研究团队统计了某地区10000名患者的相关信息,得到如表表格:
潜伏期(天)
(0,2]
(2,4]
(4,6]
(6,8]
(8,10]
(10,12]
(12,14]
人数
600
1900
3000
2500
1600
250
150
附: K2=n(ad?bc)2(a+b)(c+d)(a+c)(b+d) .
P(K2≥k0)
0.150
0.100
0.050
0.025
0.010
0.005
0.001
k0
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(1)新冠肺炎的潜伏期受诸多因素的影响,为研究潜伏期与年龄的关系,通过分层抽样从10000名患者中抽取200人进行研究,完成下面的2×2列联表,并判断能否在犯错误的概率不超过0.001的前提下认为潜伏期与患者年龄有关?
潜伏期 ≤8 天
潜伏期 >8 天
总计
60岁以上(含60岁)
150
60岁以下
30
总计
200
(2)依据上述数据,将频率作为概率,且每名患者的潜伏期是否超过8天相互独立.为了深入研究,该团队在这一地区抽取了20名患者,其中潜伏期不超过8天的人数最有可能是多少?
5.在新冠肺炎疫情得到有效控制后,某公司迅速复工复产,为扩大销售额,提升产品品质,现随机选取了100名顾客到公司体验产品,并对体验的满意度进行评分(满分100分).体验结束后,该公司将评分制作成如图所示的直方图.
(1)将评分低于80分的为“良”,80分及以上的为“优”.根据已知条件完成下面 2×2 列联表,能否在犯错误的概率不超过0.10的前提下认为体验评分为“优良”与性别有关.
良
优
合计
男
40
女
40
合计
(2)为答谢顾客参与产品体验活动,在体验度评分为 [50,60) 和 [90,100] 的顾客中用分层抽样的方法选取了6名顾客发放优惠卡.若在这6名顾客中,随机选取4名再发放纪念品,记体验评分为 [50,60) 的顾客获得纪念品数为随机变量 X ,求 X 的分布列和数学期望.
附表及公式: K2=n(ad?bc)2(a+b)(c+d)(a+c)(b+d)
P(K2≥k0)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.072
2.076
3.841
5.024
6.635
7.879
10.828
答案解析
1.【答案】 (1)解: 300×450015000=90
∴应收集90位女生的样本数据;
(2)解: (1×0.025+3×0.100+5×0.150+7×0.125+9×0.075+11×0.025)×2=5.8
∴该校学生每周平均体育运动时间的平均数约为5.8小时;
(3)解:
每周平均体育运动时间超过4小时
每周平均体育运动时间不超过4小时
总计
男
165
45
210
女
60
30
90
总计
225
75
300
∴ K2=300×(45×60?165×30)2210×90×75×225≈4.762>3.841
∴有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
【解析】
(1)根据分层抽样的定义直接求解即可;
(2)根据直方图,利用公式x=x1p1+x2p2+??+xnpn直接求解即可;
(3)根据独立性检验公式直接求解即可.
2.【答案】
(1)解:由200名学生中抽取一人抽到喜欢数学竞赛的概率为0.6,可得喜欢数学竞赛的总人数为 200×0.6=120 ,
所以
喜欢数学竞赛
不喜欢数学竞赛
合计
男生
70
50
120
女生
50
30
80
合计
120
80
200
∴k2=200×(70×30?50×50)2120×120×80×80≈0.35<2.71 ,
∴ 没有90%的把握认为喜欢数学竞赛与性别有关;
(2)解:由题意可知抽取不喜欢数学竞赛的男生有5人,女生有3人,
∴X 的可能取值为0,1,2,3,
P(X=0)=C53C83=1056=528 ;
P(X=1)=C52C31C83=3056=1528 ;
P(X=2)=C51C32C83=1556 ;
P(X=3)=C33C83=156 ;
所以X的分布列为:
X
0
1
2
3
P
528
1528
1556
156
E(X)=0×528+1×1528+2×1556+3×156=98 .
【解析】
(1)利用已知条件补充完整 2×2 列联表,再利用独立性检验的方法判断出没有90%的把握认为喜欢数学竞赛与性别有关。
(2)利用已知条件求出随机变量X可能的取值,再利用组合数公式结合古典概型求概率公式,进而求出随机变量X的分布列,再利用随机变量X的分布列结合数学期望公式,进而求出随机变量X的数学期望。
3.【答案】
(1)解: K2=n(ad?bc)2(a+b)(c+d)(a+c)(b+d)=100×(15×20?55×10)270×30×25×75≈1.587 ,
由于 1.587<2.706 ,
故没有90%以上的把握认为“长潜伏期”与年龄有关;
(2)解:若潜伏期 Z?N(7.21,2.252) ,
此时 μ+3σ=7.21+3×2.25=13.96 ,
由 P(Z≥13.96)=1?0.99742=0.0013 ,
显然潜伏期超过14天的概率很低,
因此隔离14天是合理的.
(3)解:由于100个病例中有25个属于长潜伏期,
若以样本频率估计概率,英特患者属于“长潜伏期”的概率是 14 ,
因为 X~B(4,14) ,
所以期望 E(X)=np=4×14=1 ;
方差 D(X)=np(1?p)=4×14×34=34 .
【解析】
(1)利用已知条件结合独立性检验的方法,进而判断出没有90%以上的把握认为“长潜伏期”与年龄有关。
(2)利用潜伏期 Z 服从正态分布 N(μ,σ2) , 再结合正态分布对应的函数的图象的对称性,再利用已知条件求出 P(Z≥13.96)=0.0013 ,显然潜伏期超过14天的概率很低,因此隔离14天是合理的。
(3) 以样本频率估计概率结合频率等于频数除以样本容量的公式,再结合已知条件得出英特患者属于“长潜伏期”的概率是 14 , 再利用随机变量X服从二项分布,再结合二项分布求数学期望公式和方差公式,进而求出4个病例中有 X(X∈N?) 个进入“长潜伏期”的期望与方差。?
4.【答案】
(1)解:由表中数据可知,潜伏期大于8天的人数为 1600+250+15010000×200=40 人,
补充完整的2×2列联表如下,
潜伏期 ≤8 天
潜伏期 >8 天
总计
60岁以上(含60岁)
130
20
150
60岁以下
30
20
50
总计
160
40
200
所以 K2=200×(130×20?30×20)2150×50×160×40≈16.667>10.828 ,
故能在犯错误的概率不超过0.001的前提下认为潜伏期与患者年龄有关.
(2)解:该地区10000名患者中潜伏期不超过8天的人数为 600+1900+3000+2500=8000 名,
将频率视为概率,潜伏期不超过8天的概率为 800010000=45 ,
所以抽取的20名患者中潜伏期不超过8天的人数最有可能是 20×45=16 名
【解析】
(1)先计算潜伏期大于8天的人数,完成2×2列联表,再计算K的观测值K2 , 并与附表中的数据对比,即可作出判断;
(2)将频率作为概率,计算该地区10000名患者中潜伏期不超过8天的概率,即可得解.
5.【答案】
(1)解:根据题意,评分低于80分的有 (0.01+0.01+0.02)×10×100=40 人,即评分为“良”的有 40 人,所以列联表如下:
良
优
合计
男
20
20
40
女
20
40
60
合计
40
60
100
由题得, K2=100(20×40?20×20)240×60×60×40=259≈2.78>2.706
所以,能在犯错误的概率不超过0.10的前提下认为体验评分为“优良”与性别有关.
(2)解:由已知得体验度评分为 [50,60) 和 [90,100] 的顾客分别有10人,20人,则在随机抽取的6人中评分为 [50,60) 有2人,评分为 [90,100] 有4人.
则 X 可能的取值有0,1,2.
P(X=0)=C44C64=115 , P(X=1)=C21?C43C64=815 , P(X=2)=C22?C42C64=615 ,
则 X 的分布列为
X
0
1
2
P
115
815
615
所以, E(X)=0×115+1×815+2×615=43 .
【解析】
(1)根据题意填写列联表,计算K2 , 对照附表得出结论;
(2)利用分层抽样法与列举法求出基本事件数,计算所求的概率值.
