第八章 成对数据的统计分析 讲义-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(Word含答案)
文档属性
| 名称 | 第八章 成对数据的统计分析 讲义-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(Word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 589.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 17:28:21 | ||
图片预览



文档简介
第八章 成对数据的统计分析
第八章 成对数据的统计分析
知识点1.列联表
(1).2×2列联表给出了成对分类变量数据的交叉分类频数.
(2).定义一对分类变量X和Y,我们整理数据如下表所示:
X
Y
合计
Y=0
Y=1
X=0
a
b
a+b
X=1
c
d
c+d
合计
a+c
b+d
n=a+b+c+d
像这种形式的数据统计表称为2×2列联表.
知识点2.独立性检验解决实际问题的主要环节
(1)提出零假设H0:X和Y相互独立,并给出在问题中的解释.
(2)根据抽样数据整理出2×2列联表,计算χ2的值,并与临界值xα比较.
(3)根据检验规则得出推断结论.
(4)在X和Y不独立的情况下,根据需要,通过比较相应的频率,分析X和Y间的影响规律.
知识点3.相关关系的分类
按变量间的增减性分为正相关和负相关.
①正相关:当一个变量的值增加时,另一个变量的相应值也增加
②负相关:当一个变量的值增加时,另一个变量的相应值也减少
按变量间是否有线性特征分为线性相关和非线性相关(曲线相关).
①线性相关:如果两个变量的取值呈现正相关或负相关,而且散点落在一条直线附近,我们称这两个变量线性相关;
②非线性相关或曲线相关:如果两个变量具有相关性,但不是线性相关,我们称这两个变量非线性相关
知识点4.一元线性回归模型
称为Y关于x的一元线性回归模型.其中Y称为因变量或响应变量,x称为自变量或解释变量,a称为截距参数,b称为斜率参数;e是Y与bx+a之间的随机误差,如e=0,那么Y与x之间的关系就可以用一元线性函数模型来描述.
知识点5.对模型刻画数据效果的分析
残差图法
残差图中,如残差比较均匀地集中在以横轴为对称轴的水平带状区域内,说明经验回归方程较好地刻画两个变量的关系.
残差平方和法
残差平方和(yi-i)2越小,模型的拟合效果越好.
题型探究
题型探究
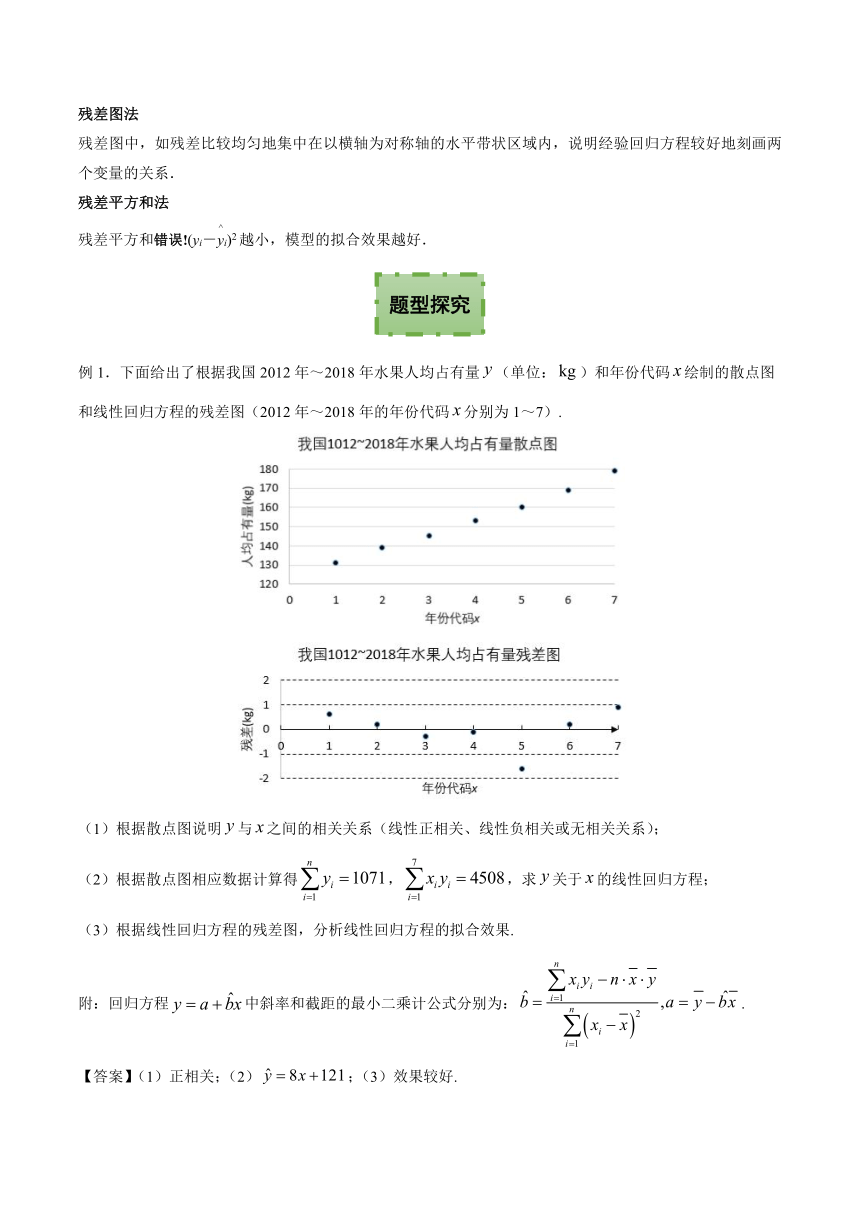
例1.下面给出了根据我国2012年~2018年水果人均占有量false(单位:false)和年份代码false绘制的散点图和线性回归方程的残差图(2012年~2018年的年份代码false分别为1~7).
(1)根据散点图说明false与false之间的相关关系(线性正相关、线性负相关或无相关关系);
(2)根据散点图相应数据计算得false,false,求false关于false的线性回归方程;
(3)根据线性回归方程的残差图,分析线性回归方程的拟合效果.
附:回归方程false中斜率和截距的最小二乘计公式分别为:false.
【答案】(1)正相关;(2)false;(3)效果较好.
【详解】
(1)false与false之间线性正相关;
(2)false,false
false
false,false
所以false关于false的线性回归方程为false.
(3)由残差图知,残差的绝对值相对于false较小,残差图均匀分布在一个较窄的带形区域内,故线性回归方程的拟合效果较好.
例2.某机构为了了解不同年龄的人对一款智能家电的评价,随机选取了50名购买该家电的消费者,让他们根据实际使用体验进行评分.
(Ⅰ)设消费者的年龄为false,对该款智能家电的评分为false.若根据统计数据,用最小二乘法得到false关于false的线性回归方程为false,且年龄false的方差为false,评分false的方差为false.求false与false的相关系数false,并据此判断对该款智能家电的评分与年龄的相关性强弱.
(Ⅱ)按照一定的标准,将50名消费者的年龄划分为“青年”和“中老年”,评分划分为“好评”和“差评”,整理得到如下数据,请判断是否有false的把握认为对该智能家电的评价与年龄有关.
好评
差评
青年
8
16
中老年
20
6
附:线性回归直线false的斜率false;相关系数false,独立性检验中的false,其中false.
临界值表:
false
0.050
0.010
0.001
false
3.841
6.635
10.828
【答案】(Ⅰ)false,相关性较强;(Ⅱ)有false的把握认为对该智能家电的评价与年龄有关.
【详解】
(Ⅰ)相关系数false
false
false.
故对该款智能家电的评分与年龄的相关性较强.
(Ⅱ)由列联表可得
false.
故有false的把握认为对该智能家电的评价与年龄有关.
例3.false指数是用体重公斤数除以身高米数的平方得出的数字,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.对于高中男体育特长生而言,当false数值大于或等于20.5时,我们说体重较重,当false数值小于20.5时,我们说体重较轻,身高大于或等于false我们说身高较高,身高小于170cm我们说身高较矮.
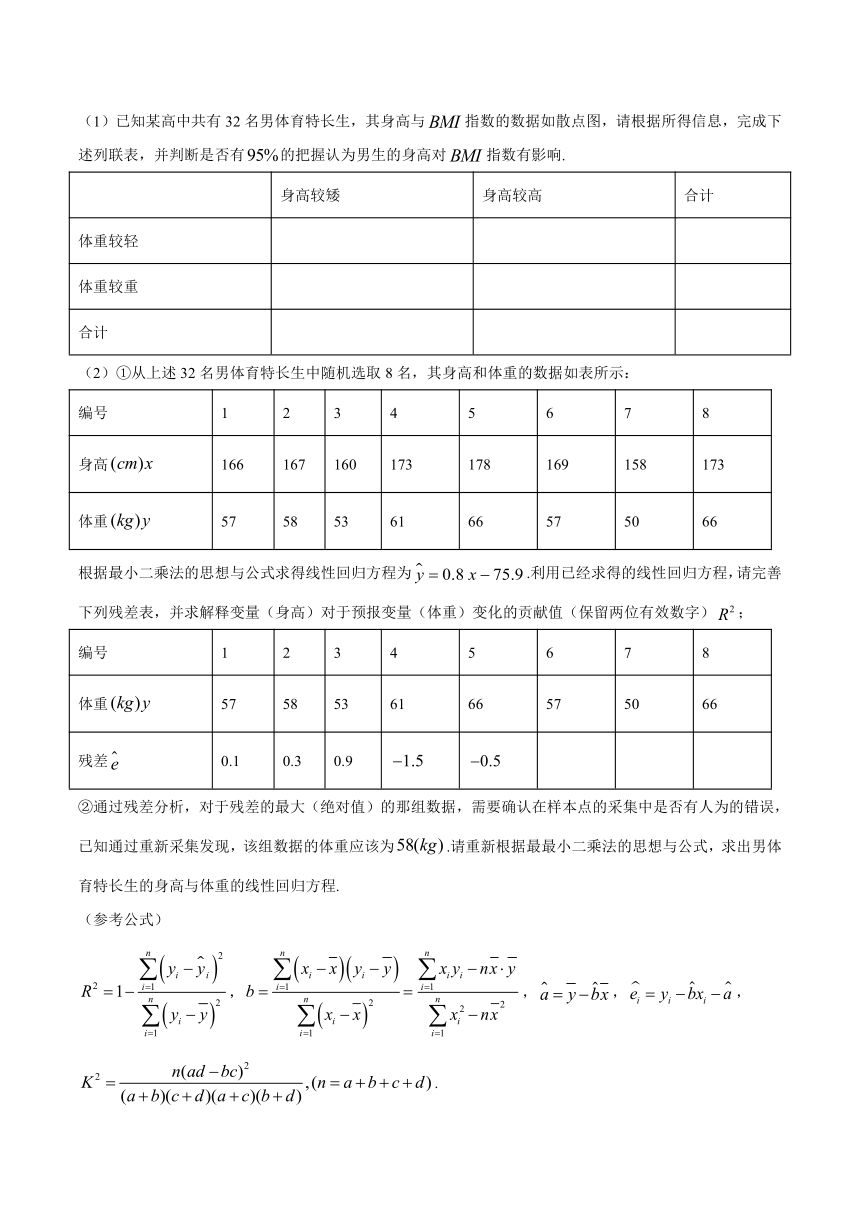
(1)已知某高中共有32名男体育特长生,其身高与false指数的数据如散点图,请根据所得信息,完成下述列联表,并判断是否有false的把握认为男生的身高对false指数有影响.
身高较矮
身高较高
合计
体重较轻
体重较重
合计
(2)①从上述32名男体育特长生中随机选取8名,其身高和体重的数据如表所示:
编号
1
2
3
4
5
6
7
8
身高false
166
167
160
173
178
169
158
173
体重false
57
58
53
61
66
57
50
66
根据最小二乘法的思想与公式求得线性回归方程为false.利用已经求得的线性回归方程,请完善下列残差表,并求解释变量(身高)对于预报变量(体重)变化的贡献值(保留两位有效数字)false;
编号
1
2
3
4
5
6
7
8
体重false
57
58
53
61
66
57
50
66
残差false
0.1
0.3
0.9
false
false
②通过残差分析,对于残差的最大(绝对值)的那组数据,需要确认在样本点的采集中是否有人为的错误,已知通过重新采集发现,该组数据的体重应该为false.请重新根据最最小二乘法的思想与公式,求出男体育特长生的身高与体重的线性回归方程.
(参考公式)
false,false,false,false,false.
(参考数据)
false,false,false,false,false.
false
0.10
0.05
0.01
0.005
false
2.706
3.811
6.635
7.879
【答案】(1)列联表见解析,没有;(2)①残差表见解析,0.91;②false
【详解】
(1)
身高较矮
身高较高
合计
体重较轻
6
15
21
体重较重
6
5
11
合计
12
20
32
由于false,
因此没有false的把握认为男生的身高对false指数有影响.
(2)①,对编号为6的数据:false,对编号为7的数据:false,对编号为8的数据false,完成残差表如下所示:
编号
1
2
3
4
5
6
7
8
体重false
57
58
53
61
66
57
50
66
残差false
0.1
0.3
0.9
false
false
false
false
3.5
falsefalse.
所以解释变量(身高)对于预报变量(体重)变化的贡献值false约为0.91.
②由①可知,第八组数据的体重应为58.
此时false,又false,false,false,
false,
false,
所以重新采集数据后,男体育特长生的身高与体重的线性回归方程为false.
例4.随着科学技术的飞速发展,网络也已经逐渐融入了人们的日常生活,网购作为一种新的消费方式,因其具有快捷、商品种类齐全、性价比高等优势而深受广大消费者认可.某网购公司统计了近五年在本公司网购的人数,得到如下的相关数据(其中“x=1”表示2015年,“x=2”表示2016年,依次类推;y表示人数):
x
1
2
3
4
5
y(万人)
20
50
100
150
180
(1)试根据表中的数据,求出y关于x的线性回归方程,并预测到哪一年该公司的网购人数能超过300万人;
(2)该公司为了吸引网购者,特别推出“玩网络游戏,送免费购物券”活动,网购者可根据抛掷骰子的结果,操控微型遥控车在方格图上行进. 若遥控车最终停在“胜利大本营”,则网购者可获得免费购物券500元;若遥控车最终停在“失败大本营”,则网购者可获得免费购物券200元. 已知骰子出现奇数与偶数的概率都是false,方格图上标有第0格、第1格、第2格、…、第20格。遥控车开始在第0格,网购者每抛掷一次骰子,遥控车向前移动一次.若掷出奇数,遥控车向前移动一格(从false到false)若掷出偶数遥控车向前移动两格(从false到false),直到遥控车移到第19格胜利大本营)或第20格(失败大本营)时,游戏结束。设遥控车移到第false格的概率为false,试证明false是等比数列,并求网购者参与游戏一次获得免费购物券金额的期望值.
附:在线性回归方程false中,false.
【答案】(1)false,预计到2022年该公司的网购人数能超过300万人;
(2)约400元.
【详解】
解:(1)false
false
false
false
故false 从而false
所以所求线性回归方程为false,
令false,解得false.
故预计到2022年该公司的网购人数能超过300万人
(2)遥控车开始在第0格为必然事件,false,第一次掷骰子出现奇数,遥控车移到第一格,其概率为false,即false.遥控车移到第false(false)格的情况是下列两种,而且也只有两种.
①遥控车先到第false格,又掷出奇数,其概率为false
②遥控车先到第false格,又掷出偶数,其概率为false
所以false,false
false当false时,数列false是公比为false的等比数列
false
以上各式相加,得falsefalse
false(false),
false获胜的概率false
失败的概率false
false设参与游戏一次的顾客获得优惠券金额为false元,false或false
falseX的期望false
false参与游戏一次的顾客获得优惠券金额的期望值为false,约400元.
课后小练
课后小练
1.某市消防部门对辖区企业员工进行了一次消防安全知识问卷调查,通过随机抽样,得到参加问卷调查的500人(其中300人为女性)的得分(满分100false数据,统计结果如表所示:
得分
false
false
false
false
false
false
男性人数
20
60
40
40
30
10
女性人数
10
70
60
75
50
35
(1)把员工分为对消防知识“比较熟悉”(不低于70分的)和“不太熟悉”(低于70分的)两类,请完成如下false列联表,并判断是否有false的把握认为该企业员工对消防知识的熟悉程度与性别有关?
不太熟悉
比较熟悉
合计
男性
女性
合计
(2)为增加员工消防安全知识及自救?自防能力,现将企业员工分成两人一组开展“消防安全技能趣味知识”竞赛.在每轮比赛中,小组两位成员各答两道题目,若他们答对题目个数和不少于3个,则小组积1分,否则积0分.已知false与false在同一小组,false答对每道题的概率为false答对每道题的概率为false,且false,理论上至少要进行多少轮比赛才能使false所在的小组的积分的期望值不少于5分?附:参考公式及false检验临界值表
false
false
false
false
false
false
false
false
false
false
false
false
false
false
false
false
false
2.2021年2月25日举行的全国脱贫攻坚总结表彰大会上,国家电网共有23名(个)先进个人、先进集体获得表彰.其中,国网西藏电力有限公司农电工作部从习近平总书记手中接过了“全国脱贫攻坚楷模”奖牌.过去8年,在党中央坚强领导下,经过世界规模最大、力度最强的脱贫攻坚战,近1亿人摆脱绝对贫困.长期以来贫困地区的农产品面临“种得出卖不出”“酒香也怕巷子深”的困境.深谙互联网思维的国家电网人,搭平台、建渠道,以一款APP让众多贫困地区的产品销售易如反掌.2020年“6.18”期间,带货主播和直播运营两大岗位高达去年同期的11.6倍.针对这一市场现象,为了加强监管,相关管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出100次成功交易,并对其评价进行统计,对商品的好评率为0.6,对商品和服务都做出好评的交易为40次,对商品和服务部不满意的交易为5次.
(1)请完成关于商品和服务评价的false列联表,并判断能否在犯错误的概率不超过0.025的前提下,认为商品好与服务好评有关?
对服务好评
对服务不满意
合计
对商品好评
40
对商品不满意
5
合计
100
(2)从“对服务不满意”的评价中分层选出10个,再从这10个评价中随机选出6个,记其中“对商品不满意”的个数为false,求false的分布列及数学期望.
附:false,false.
false
0.15
0.10
0.05
0.025
0.010
0.005
0.001
false
2.072
2.706
3.841
5.024
6.635
7.879
10.828
3.2021年1月1日,新中国成立以来第一部以“法典”命名的法律《中华人民共和国民法典》颁布施行,我国将正式迈入“民法典”时代,为深入了解《民法典》,大力营造学法守法用法的良好氛围,高三年级从文科班和理科班的学生中随机抽取了100名同学参加学校举办的“民法典与你同行”知识竞赛,将他们的比赛成绩(满分为100分)分为6组:false,false,false,false,false,false,得到如图所示的频率分布直方图.
(1)求false的值;
(2)估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
(3)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”,请将下面的false列联表补充完整,并判断是否有95%的把握认为“比赛成绩是否优秀与文理科别有关”?
优秀
非优秀
合计
文科生
30
理科生
55
合计
100
参考公式及数据:false,false
false(false)
0.10
0.05
0.025
0.010
0.005
0.001
false
2.706
3.841
5.024
6.635
7.879
10.828
4.2021年是“十四五”开局之年,是实施乡村振兴的重要一年.某县为振兴乡村经济,大力发展乡村生态旅游,激发乡村发展活力.该县为了解乡村生态旅游发展情况,现对全县乡村生态旅游进行调研,统计了近9个月来每月到该县乡村生态旅游的外地游客人数false(单位:万人),并绘制成下图所示散点图,其中月份代码1~9分别对应2020年7月至2021年3月.
(1)用模型①false,②false分别拟合false与false的关系,根据散点图判断,哪个模型的拟合效果最好?(不必说理由)
(2)根据(1)中选择的模型,求false关于false的回归方程(系数精确到0.01);
(3)据以往数据统计,每位外地游客可为该县带来100元左右的旅游收入,根据(2)中的回归模型,预测2021年10月,外地游客可为该县带来的生态旅游收入为多少万元?
参考数据:下表中false,false.
false
false
false
false
false
false
23
2.15
60
3.58
84.5
21.31
参考公式:对于一组数据false,false,…,false,回归方程false中的斜率和截距的最小二乘估计公式分别为false,false.
5.false年开始,小李在县城租房开了一间服装店,每年只卖甲品牌和乙品牌的服装.小李所租服装店每年的租金如下表:
年份
false
false
false
false
年份代号false
false
false
false
false
租金false(千元)
false
false
false
false
根据以往的统计可知,每年卖甲品牌服装的收入为false万元,卖乙品牌服装的收入为false万元.
(I)求false关于false的线性回归方程;
(II)由(I)求得的回归方程预测此服装店false年的利润为多少.(年利润false年收入false年租金)
参考公式:在线性回归方程false中,false,false.
参考答案
1.(1)填表见解析;有false的把握认为该企业员工对消防知识的了解程度与性别有关;(2)理论上至少要进行16轮比赛.
【详解】
(1)
不太熟悉
比较熟悉
合计
男性
120
80
200
女性
140
160
300
合计
260
240
500
false
false有false的把握认为该企业员工对消防知识的了解程度与性别有关.
(2)false在一轮比赛中积1分的概率为false
false,
又false,则false
false,且false
false,此时false,
设false所在的小组在false轮比赛中的积分为false,则false,
false,所以理论上至少要进行16轮比赛.
2.(1)列联表见解析,能;(2)分布列见解析,false.
【详解】
(1)由题意可得关于商品和服务评价的false列联表如下:
对服务好评
对服务不满意
合计
对商品好评
40
20
60
对商品不满意
35
5
40
合计
75
25
100
false,
故能在犯错误的概率不超过0.025的前提下,认为商品好评与服务好评有关.
(2)由(1)得从“对服务不满意”的评价中分层选出的10个评价中,“对商品好评”的有8个,“对商品不满意”的有2个,故false的所有可能取值为0,1,2,
false,false,false,
false
0
1
2
false
false
false
false
所以false.
3.(1)false;(2)false;(3)列联表答案见解析,没有95%的把握认为“比赛成绩是否优秀与科别有关”.
【详解】
解:(1)由题可得false,解得false;
(2)平均成绩为:false;
(3)由(2)知,在抽取的100名学生中,比赛成绩优秀的有false人,
由此可得完整的false列联表:
优秀
非优秀
合计
文科生
15
30
45
理科生
10
45
55
合计
25
75
100
∵false,
∴没有95%的把握认为“比赛成绩是否优秀与科别有关”.
4.(1)模型②false的拟合效果最好;(2)false;(3)3400万元.
【详解】
(1)模型②false的拟合效果最好.
(2)令false,知false与false可用线性方false拟合,则
false,false,
所以,false关于false的线性回归方程为false,
故false关于x的回归方程为false.
(3)2021年10月,即false时,false(万人),
此时,外地游客可为该县带来的生态旅游收入为3400万元.
5.(I)false;(II)14.45万元.
【详解】
命题意图 本题考查线性回归方程.
解析(I)根据表中数据,计算可得false,false,
false,
false
false,
false,
false关于false的线性回归方程为false
(II)将false代入回归方程得false(千元).
false预测第false年卖甲品牌服装的收入为false万元,卖乙品牌服装的收入为false万元,
false预测false年的利润为false(万元).
第八章 成对数据的统计分析
知识点1.列联表
(1).2×2列联表给出了成对分类变量数据的交叉分类频数.
(2).定义一对分类变量X和Y,我们整理数据如下表所示:
X
Y
合计
Y=0
Y=1
X=0
a
b
a+b
X=1
c
d
c+d
合计
a+c
b+d
n=a+b+c+d
像这种形式的数据统计表称为2×2列联表.
知识点2.独立性检验解决实际问题的主要环节
(1)提出零假设H0:X和Y相互独立,并给出在问题中的解释.
(2)根据抽样数据整理出2×2列联表,计算χ2的值,并与临界值xα比较.
(3)根据检验规则得出推断结论.
(4)在X和Y不独立的情况下,根据需要,通过比较相应的频率,分析X和Y间的影响规律.
知识点3.相关关系的分类
按变量间的增减性分为正相关和负相关.
①正相关:当一个变量的值增加时,另一个变量的相应值也增加
②负相关:当一个变量的值增加时,另一个变量的相应值也减少
按变量间是否有线性特征分为线性相关和非线性相关(曲线相关).
①线性相关:如果两个变量的取值呈现正相关或负相关,而且散点落在一条直线附近,我们称这两个变量线性相关;
②非线性相关或曲线相关:如果两个变量具有相关性,但不是线性相关,我们称这两个变量非线性相关
知识点4.一元线性回归模型
称为Y关于x的一元线性回归模型.其中Y称为因变量或响应变量,x称为自变量或解释变量,a称为截距参数,b称为斜率参数;e是Y与bx+a之间的随机误差,如e=0,那么Y与x之间的关系就可以用一元线性函数模型来描述.
知识点5.对模型刻画数据效果的分析
残差图法
残差图中,如残差比较均匀地集中在以横轴为对称轴的水平带状区域内,说明经验回归方程较好地刻画两个变量的关系.
残差平方和法
残差平方和(yi-i)2越小,模型的拟合效果越好.
题型探究
题型探究
例1.下面给出了根据我国2012年~2018年水果人均占有量false(单位:false)和年份代码false绘制的散点图和线性回归方程的残差图(2012年~2018年的年份代码false分别为1~7).
(1)根据散点图说明false与false之间的相关关系(线性正相关、线性负相关或无相关关系);
(2)根据散点图相应数据计算得false,false,求false关于false的线性回归方程;
(3)根据线性回归方程的残差图,分析线性回归方程的拟合效果.
附:回归方程false中斜率和截距的最小二乘计公式分别为:false.
【答案】(1)正相关;(2)false;(3)效果较好.
【详解】
(1)false与false之间线性正相关;
(2)false,false
false
false,false
所以false关于false的线性回归方程为false.
(3)由残差图知,残差的绝对值相对于false较小,残差图均匀分布在一个较窄的带形区域内,故线性回归方程的拟合效果较好.
例2.某机构为了了解不同年龄的人对一款智能家电的评价,随机选取了50名购买该家电的消费者,让他们根据实际使用体验进行评分.
(Ⅰ)设消费者的年龄为false,对该款智能家电的评分为false.若根据统计数据,用最小二乘法得到false关于false的线性回归方程为false,且年龄false的方差为false,评分false的方差为false.求false与false的相关系数false,并据此判断对该款智能家电的评分与年龄的相关性强弱.
(Ⅱ)按照一定的标准,将50名消费者的年龄划分为“青年”和“中老年”,评分划分为“好评”和“差评”,整理得到如下数据,请判断是否有false的把握认为对该智能家电的评价与年龄有关.
好评
差评
青年
8
16
中老年
20
6
附:线性回归直线false的斜率false;相关系数false,独立性检验中的false,其中false.
临界值表:
false
0.050
0.010
0.001
false
3.841
6.635
10.828
【答案】(Ⅰ)false,相关性较强;(Ⅱ)有false的把握认为对该智能家电的评价与年龄有关.
【详解】
(Ⅰ)相关系数false
false
false.
故对该款智能家电的评分与年龄的相关性较强.
(Ⅱ)由列联表可得
false.
故有false的把握认为对该智能家电的评价与年龄有关.
例3.false指数是用体重公斤数除以身高米数的平方得出的数字,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.对于高中男体育特长生而言,当false数值大于或等于20.5时,我们说体重较重,当false数值小于20.5时,我们说体重较轻,身高大于或等于false我们说身高较高,身高小于170cm我们说身高较矮.
(1)已知某高中共有32名男体育特长生,其身高与false指数的数据如散点图,请根据所得信息,完成下述列联表,并判断是否有false的把握认为男生的身高对false指数有影响.
身高较矮
身高较高
合计
体重较轻
体重较重
合计
(2)①从上述32名男体育特长生中随机选取8名,其身高和体重的数据如表所示:
编号
1
2
3
4
5
6
7
8
身高false
166
167
160
173
178
169
158
173
体重false
57
58
53
61
66
57
50
66
根据最小二乘法的思想与公式求得线性回归方程为false.利用已经求得的线性回归方程,请完善下列残差表,并求解释变量(身高)对于预报变量(体重)变化的贡献值(保留两位有效数字)false;
编号
1
2
3
4
5
6
7
8
体重false
57
58
53
61
66
57
50
66
残差false
0.1
0.3
0.9
false
false
②通过残差分析,对于残差的最大(绝对值)的那组数据,需要确认在样本点的采集中是否有人为的错误,已知通过重新采集发现,该组数据的体重应该为false.请重新根据最最小二乘法的思想与公式,求出男体育特长生的身高与体重的线性回归方程.
(参考公式)
false,false,false,false,false.
(参考数据)
false,false,false,false,false.
false
0.10
0.05
0.01
0.005
false
2.706
3.811
6.635
7.879
【答案】(1)列联表见解析,没有;(2)①残差表见解析,0.91;②false
【详解】
(1)
身高较矮
身高较高
合计
体重较轻
6
15
21
体重较重
6
5
11
合计
12
20
32
由于false,
因此没有false的把握认为男生的身高对false指数有影响.
(2)①,对编号为6的数据:false,对编号为7的数据:false,对编号为8的数据false,完成残差表如下所示:
编号
1
2
3
4
5
6
7
8
体重false
57
58
53
61
66
57
50
66
残差false
0.1
0.3
0.9
false
false
false
false
3.5
falsefalse.
所以解释变量(身高)对于预报变量(体重)变化的贡献值false约为0.91.
②由①可知,第八组数据的体重应为58.
此时false,又false,false,false,
false,
false,
所以重新采集数据后,男体育特长生的身高与体重的线性回归方程为false.
例4.随着科学技术的飞速发展,网络也已经逐渐融入了人们的日常生活,网购作为一种新的消费方式,因其具有快捷、商品种类齐全、性价比高等优势而深受广大消费者认可.某网购公司统计了近五年在本公司网购的人数,得到如下的相关数据(其中“x=1”表示2015年,“x=2”表示2016年,依次类推;y表示人数):
x
1
2
3
4
5
y(万人)
20
50
100
150
180
(1)试根据表中的数据,求出y关于x的线性回归方程,并预测到哪一年该公司的网购人数能超过300万人;
(2)该公司为了吸引网购者,特别推出“玩网络游戏,送免费购物券”活动,网购者可根据抛掷骰子的结果,操控微型遥控车在方格图上行进. 若遥控车最终停在“胜利大本营”,则网购者可获得免费购物券500元;若遥控车最终停在“失败大本营”,则网购者可获得免费购物券200元. 已知骰子出现奇数与偶数的概率都是false,方格图上标有第0格、第1格、第2格、…、第20格。遥控车开始在第0格,网购者每抛掷一次骰子,遥控车向前移动一次.若掷出奇数,遥控车向前移动一格(从false到false)若掷出偶数遥控车向前移动两格(从false到false),直到遥控车移到第19格胜利大本营)或第20格(失败大本营)时,游戏结束。设遥控车移到第false格的概率为false,试证明false是等比数列,并求网购者参与游戏一次获得免费购物券金额的期望值.
附:在线性回归方程false中,false.
【答案】(1)false,预计到2022年该公司的网购人数能超过300万人;
(2)约400元.
【详解】
解:(1)false
false
false
false
故false 从而false
所以所求线性回归方程为false,
令false,解得false.
故预计到2022年该公司的网购人数能超过300万人
(2)遥控车开始在第0格为必然事件,false,第一次掷骰子出现奇数,遥控车移到第一格,其概率为false,即false.遥控车移到第false(false)格的情况是下列两种,而且也只有两种.
①遥控车先到第false格,又掷出奇数,其概率为false
②遥控车先到第false格,又掷出偶数,其概率为false
所以false,false
false当false时,数列false是公比为false的等比数列
false
以上各式相加,得falsefalse
false(false),
false获胜的概率false
失败的概率false
false设参与游戏一次的顾客获得优惠券金额为false元,false或false
falseX的期望false
false参与游戏一次的顾客获得优惠券金额的期望值为false,约400元.
课后小练
课后小练
1.某市消防部门对辖区企业员工进行了一次消防安全知识问卷调查,通过随机抽样,得到参加问卷调查的500人(其中300人为女性)的得分(满分100false数据,统计结果如表所示:
得分
false
false
false
false
false
false
男性人数
20
60
40
40
30
10
女性人数
10
70
60
75
50
35
(1)把员工分为对消防知识“比较熟悉”(不低于70分的)和“不太熟悉”(低于70分的)两类,请完成如下false列联表,并判断是否有false的把握认为该企业员工对消防知识的熟悉程度与性别有关?
不太熟悉
比较熟悉
合计
男性
女性
合计
(2)为增加员工消防安全知识及自救?自防能力,现将企业员工分成两人一组开展“消防安全技能趣味知识”竞赛.在每轮比赛中,小组两位成员各答两道题目,若他们答对题目个数和不少于3个,则小组积1分,否则积0分.已知false与false在同一小组,false答对每道题的概率为false答对每道题的概率为false,且false,理论上至少要进行多少轮比赛才能使false所在的小组的积分的期望值不少于5分?附:参考公式及false检验临界值表
false
false
false
false
false
false
false
false
false
false
false
false
false
false
false
false
false
2.2021年2月25日举行的全国脱贫攻坚总结表彰大会上,国家电网共有23名(个)先进个人、先进集体获得表彰.其中,国网西藏电力有限公司农电工作部从习近平总书记手中接过了“全国脱贫攻坚楷模”奖牌.过去8年,在党中央坚强领导下,经过世界规模最大、力度最强的脱贫攻坚战,近1亿人摆脱绝对贫困.长期以来贫困地区的农产品面临“种得出卖不出”“酒香也怕巷子深”的困境.深谙互联网思维的国家电网人,搭平台、建渠道,以一款APP让众多贫困地区的产品销售易如反掌.2020年“6.18”期间,带货主播和直播运营两大岗位高达去年同期的11.6倍.针对这一市场现象,为了加强监管,相关管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出100次成功交易,并对其评价进行统计,对商品的好评率为0.6,对商品和服务都做出好评的交易为40次,对商品和服务部不满意的交易为5次.
(1)请完成关于商品和服务评价的false列联表,并判断能否在犯错误的概率不超过0.025的前提下,认为商品好与服务好评有关?
对服务好评
对服务不满意
合计
对商品好评
40
对商品不满意
5
合计
100
(2)从“对服务不满意”的评价中分层选出10个,再从这10个评价中随机选出6个,记其中“对商品不满意”的个数为false,求false的分布列及数学期望.
附:false,false.
false
0.15
0.10
0.05
0.025
0.010
0.005
0.001
false
2.072
2.706
3.841
5.024
6.635
7.879
10.828
3.2021年1月1日,新中国成立以来第一部以“法典”命名的法律《中华人民共和国民法典》颁布施行,我国将正式迈入“民法典”时代,为深入了解《民法典》,大力营造学法守法用法的良好氛围,高三年级从文科班和理科班的学生中随机抽取了100名同学参加学校举办的“民法典与你同行”知识竞赛,将他们的比赛成绩(满分为100分)分为6组:false,false,false,false,false,false,得到如图所示的频率分布直方图.
(1)求false的值;
(2)估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
(3)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”,请将下面的false列联表补充完整,并判断是否有95%的把握认为“比赛成绩是否优秀与文理科别有关”?
优秀
非优秀
合计
文科生
30
理科生
55
合计
100
参考公式及数据:false,false
false(false)
0.10
0.05
0.025
0.010
0.005
0.001
false
2.706
3.841
5.024
6.635
7.879
10.828
4.2021年是“十四五”开局之年,是实施乡村振兴的重要一年.某县为振兴乡村经济,大力发展乡村生态旅游,激发乡村发展活力.该县为了解乡村生态旅游发展情况,现对全县乡村生态旅游进行调研,统计了近9个月来每月到该县乡村生态旅游的外地游客人数false(单位:万人),并绘制成下图所示散点图,其中月份代码1~9分别对应2020年7月至2021年3月.
(1)用模型①false,②false分别拟合false与false的关系,根据散点图判断,哪个模型的拟合效果最好?(不必说理由)
(2)根据(1)中选择的模型,求false关于false的回归方程(系数精确到0.01);
(3)据以往数据统计,每位外地游客可为该县带来100元左右的旅游收入,根据(2)中的回归模型,预测2021年10月,外地游客可为该县带来的生态旅游收入为多少万元?
参考数据:下表中false,false.
false
false
false
false
false
false
23
2.15
60
3.58
84.5
21.31
参考公式:对于一组数据false,false,…,false,回归方程false中的斜率和截距的最小二乘估计公式分别为false,false.
5.false年开始,小李在县城租房开了一间服装店,每年只卖甲品牌和乙品牌的服装.小李所租服装店每年的租金如下表:
年份
false
false
false
false
年份代号false
false
false
false
false
租金false(千元)
false
false
false
false
根据以往的统计可知,每年卖甲品牌服装的收入为false万元,卖乙品牌服装的收入为false万元.
(I)求false关于false的线性回归方程;
(II)由(I)求得的回归方程预测此服装店false年的利润为多少.(年利润false年收入false年租金)
参考公式:在线性回归方程false中,false,false.
参考答案
1.(1)填表见解析;有false的把握认为该企业员工对消防知识的了解程度与性别有关;(2)理论上至少要进行16轮比赛.
【详解】
(1)
不太熟悉
比较熟悉
合计
男性
120
80
200
女性
140
160
300
合计
260
240
500
false
false有false的把握认为该企业员工对消防知识的了解程度与性别有关.
(2)false在一轮比赛中积1分的概率为false
false,
又false,则false
false,且false
false,此时false,
设false所在的小组在false轮比赛中的积分为false,则false,
false,所以理论上至少要进行16轮比赛.
2.(1)列联表见解析,能;(2)分布列见解析,false.
【详解】
(1)由题意可得关于商品和服务评价的false列联表如下:
对服务好评
对服务不满意
合计
对商品好评
40
20
60
对商品不满意
35
5
40
合计
75
25
100
false,
故能在犯错误的概率不超过0.025的前提下,认为商品好评与服务好评有关.
(2)由(1)得从“对服务不满意”的评价中分层选出的10个评价中,“对商品好评”的有8个,“对商品不满意”的有2个,故false的所有可能取值为0,1,2,
false,false,false,
false
0
1
2
false
false
false
false
所以false.
3.(1)false;(2)false;(3)列联表答案见解析,没有95%的把握认为“比赛成绩是否优秀与科别有关”.
【详解】
解:(1)由题可得false,解得false;
(2)平均成绩为:false;
(3)由(2)知,在抽取的100名学生中,比赛成绩优秀的有false人,
由此可得完整的false列联表:
优秀
非优秀
合计
文科生
15
30
45
理科生
10
45
55
合计
25
75
100
∵false,
∴没有95%的把握认为“比赛成绩是否优秀与科别有关”.
4.(1)模型②false的拟合效果最好;(2)false;(3)3400万元.
【详解】
(1)模型②false的拟合效果最好.
(2)令false,知false与false可用线性方false拟合,则
false,false,
所以,false关于false的线性回归方程为false,
故false关于x的回归方程为false.
(3)2021年10月,即false时,false(万人),
此时,外地游客可为该县带来的生态旅游收入为3400万元.
5.(I)false;(II)14.45万元.
【详解】
命题意图 本题考查线性回归方程.
解析(I)根据表中数据,计算可得false,false,
false,
false
false,
false,
false关于false的线性回归方程为false
(II)将false代入回归方程得false(千元).
false预测第false年卖甲品牌服装的收入为false万元,卖乙品牌服装的收入为false万元,
false预测false年的利润为false(万元).
