第九章专题训练—统计-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册专项训练(Word含答案解析)
文档属性
| 名称 | 第九章专题训练—统计-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册专项训练(Word含答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 00:00:00 | ||
图片预览




文档简介
第九章专题训练—统计
一.单选题
1.从2019年末开始,新型冠状病毒在全球肆虐.为了研制新型冠状病毒疫苗,某大型药企需要从150名志愿者中抽取15名志愿者进行临床试验,现采用分层抽样的方法进行抽取,若这150名志愿者中老年人的人数为50人,则老年人中被抽到进行临床试验的人数是
A.15 B.10 C.5 D.1
2.某班60名同学中选出4人参加户外活动,利用随机数表法抽取样本时,先将60名同学按01,02,,60进行编号,然后从随机数表第1行的第5列和第6列数字开始从左往右依次选取两个数字,则选出的第4个同学的编号为
0347 4373 8636 9647 3661 4698 6371 6297
7424 6292 4281 1457 2042 5332 3732 1676
(注表中的数据为随机数表的第一行和第二行)
A.24 B.36 C.46 D.47
3.有17名同学参加百米竞赛,预赛成绩各不相同,要取前8名参加决赛,小明同学已经知道了自己的成绩,为了判断自己是否能进入决赛,他还需要知道17名同学成绩的
A.平均数 B.众数 C.中位数 D.方差
4.随着互联网和物流行业的快速发展,快递业务已经成为人们日常生活当中不可或缺的重要组成部分.如图是年我国快递业务量变化情况统计图,则关于这9年的统计信息,下列说法正确的是
A.这9年我国快递业务量有增有减
B.这9年我国快递业务量同比增速的中位数为
C.这9年我国快递业务量同比增速的极差未超过
D.这9年我国快递业务量的平均数超过210亿件
5.第31届世界大学生夏季运动会将于2021年8月在成都举行,举办方将招募志愿者在赛事期间为运动会提供咨询、交通引导、场馆周边秩序维护等服务.招募的志愿者需接受专业培训,甲、乙两名志愿者在培训过程中进行了六次测试,其测试成绩(单位:分)如折线图所示,则下列说法正确的是
A.甲成绩的中位数比乙成绩的中位数大
B.甲成绩的众数比乙成绩的众数小
C.甲成绩的极差比乙成绩的极差小
D.乙的成绩比甲的成绩稳定
6.空气质量的指数是反映空气质量状况的指数,指数的值越小,表明空气质量越好.指数不超过50,空气质量为“优”; 指数大于50,且不超过100,空气质量为“良”; 指数大于100,空气质量为“污染”.如图是某市2020年空气质量指数的月折线图.下列关于该市2020年空气质量的叙述中不一定正确的
A.全年的平均指数对应的空气质量等级为优或良
B.每月都至少有一天空气质量为优
C.2月,8月,9月和12月均出现污染天气
D.空气质量为“污染”的天数最多的月份是2月份
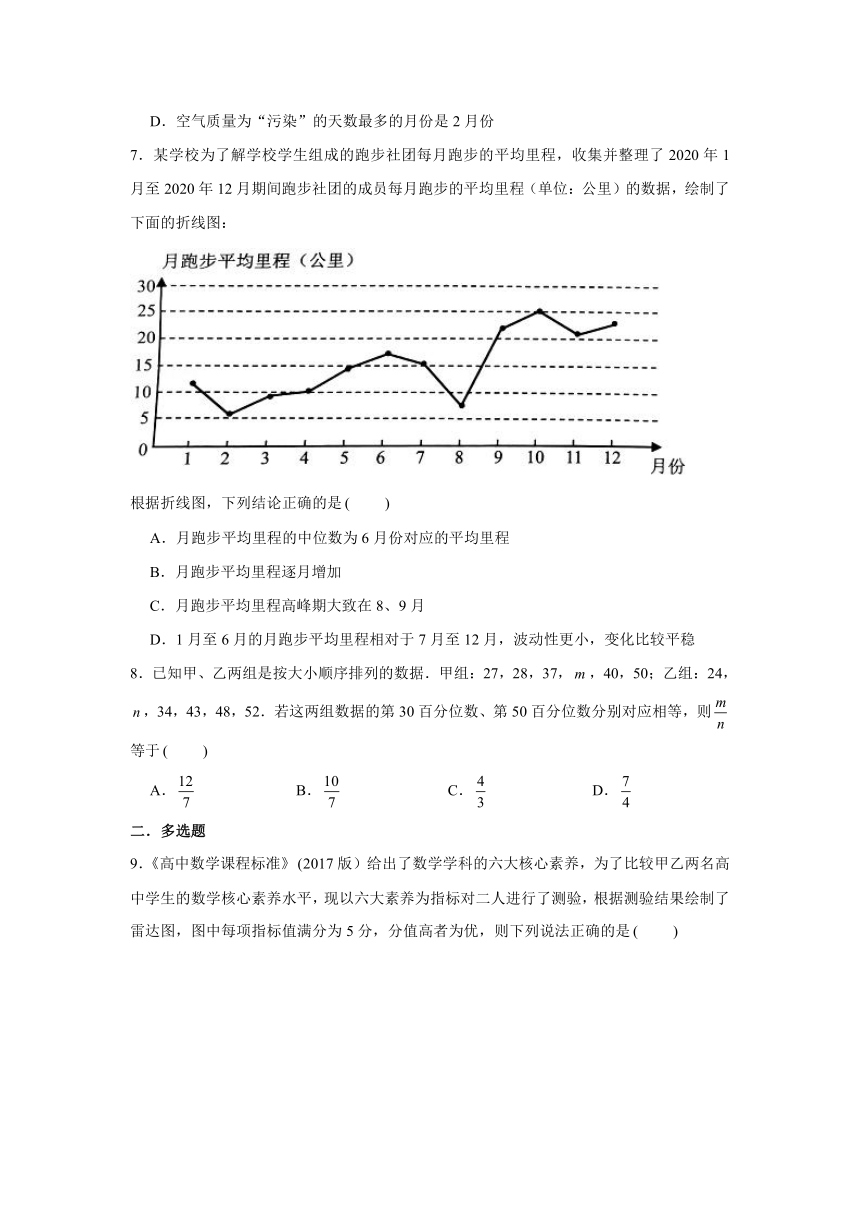
7.某学校为了解学校学生组成的跑步社团每月跑步的平均里程,收集并整理了2020年1月至2020年12月期间跑步社团的成员每月跑步的平均里程(单位:公里)的数据,绘制了下面的折线图:
根据折线图,下列结论正确的是
A.月跑步平均里程的中位数为6月份对应的平均里程
B.月跑步平均里程逐月增加
C.月跑步平均里程高峰期大致在8、9月
D.1月至6月的月跑步平均里程相对于7月至12月,波动性更小,变化比较平稳
8.已知甲、乙两组是按大小顺序排列的数据.甲组:27,28,37,,40,50;乙组:24,,34,43,48,52.若这两组数据的第30百分位数、第50百分位数分别对应相等,则等于
A. B. C. D.
二.多选题
9.《高中数学课程标准》版)给出了数学学科的六大核心素养,为了比较甲乙两名高中学生的数学核心素养水平,现以六大素养为指标对二人进行了测验,根据测验结果绘制了雷达图,图中每项指标值满分为5分,分值高者为优,则下列说法正确的是
A.甲的数学运算素养优于乙的数学运算素养
B.甲的逻辑推理素养优于乙的逻辑推理素养
C.甲的六个核心素养中只有数学运算水平最高
D.乙的六个核心素养中只有数据分析水平最高
10.为了了解市民对各种垃圾进行分类的情况,加强垃圾分类宣传的针对性,指导市民尽快掌握垃圾分类的方法,某市垃圾处理厂连续8周对有害垃圾错误分类情况进行了调查.经整理绘制了如图所示的有害垃圾错误分类重量累积统计图,图中横轴表示时间(单位:周),纵轴表示有害垃圾错误分类的累积重量(单位:吨).根据统计图分析,下列结论正确的是
A.当,时有害垃圾错误分类的重量加速增长
B.当,时有害垃圾错误分类的重量匀速增长
C.当,时有害垃圾错误分类的重量相对于当,时增长了
D.当,时有害垃圾错误分类的重量相对于当,时减少了0.6吨
11.某网络销售平台,实施对口扶贫,销售某县扶贫农产品.根据2020年全年该县扶贫农产品的销售额(单位:万元)和扶贫农产品销售额占总销售额的百分比,绘制了如图的双层饼图.根据双层饼图(季度和月份后面标注的是销售额或销售额占总销售额的百分比),下列说法正确的是
A.2020年的总销售额为1000万元
B.2月份的销售额为8万元
C.4季度销售额为280万元
D.12个月的销售额的中位数为90万元
12.在疫情防护知识竞赛中,对某校的2000名考生的参赛成绩进行统计,可得到如图所示的频率分布直方图,其中分组的区间为,,,,,,,,,,,,60分以下视为不及格,若同一组中数据用该组区间中间值作代表值,则下列说法中正确的是
A.考生竞赛成绩的众数为75分
B.不及格的考生人数为500
C.考生竞赛成绩的平均数为72.5分
D.考生竞赛成绩的中位数为75分
三.填空题
13.某地区有高中学生2400人,初中学生10900人,小学生11000人,此地教育局为了了解本地区中小学生的近视情况及其形成原因,要从本地区抽取的学生进行调查,则按分层抽样的方法抽取高中学生,初中学生和小学生的人数分别是 , , .
14.某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.若下面是尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示),则样本容量为 ,的值为 .
组别 分组 频数 频率
第1组 , 8 0.16
第2组 ,
▓
第3组 , 20 0.40
第4组 , ▓ 0.08
第5组 , 2
合计 ▓ ▓
15.某班40名学生,在一次考试中统计所得平均分为80分,方差为70,后来发现有两名同学的成绩有误,甲实得80分错记为60分,乙实得70分错记为90分,则更正后的方差为 .
16.已知某地区中小学生人数和近视情况分别如图甲和乙所示.为了了解该地区中小学生的近视形成原因,用分层抽样的方法抽取的学生进行调查,则样本容量为 ;抽取的高中生中近视的人数为 .
四.解答题
17.某校对120名考生的数学竞赛成绩进行统计,分成,,,,,,,,,五组,得到如图所示频率分布直方图.
(1)求图中的值;
(2)估计该校学生数学竞赛成绩的平均数;
(3)估计该校学生数学竞赛成绩的第80百分位数落在哪一组.
18.某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的100件产品作为样本称出它们的质量(单位:克),质量的分组区间为,,,,,,,由此得到样本的频率分布直方图如图所示.
(1)估计这条生产流水线上,质量超过515克的产品的比例;
(2)求这条生产流水线上产品质量的平均数和方差的估计值(同一组中的数据用该组区间的中点值作代表).
第九章专题训练—统计 答案
1.解:某大型药企需要从150名志愿者中抽取15名志愿者进行临床试验,
现采用分层抽样的方法进行抽取,
若这150名志愿者中老年人的人数为50人,
则老年人中被抽到进行临床试验的人数是:.
故选:.
2.解:由题知从随机数表的第1行第5列和第6列数字开始,
由表可知依次选取43,36,47,46,24.
故选:.
3.解:因为共有17个人,且他们的分数各不相同,第9名的成绩是中位数,
故要判断是否能进入决赛,他还需要知道17名同学成绩的中位数.
故选:.
4.解:由条形图可得,这9年我国快递业务量逐年增加,故错误;
将各年我国快递业务量同比增速按从小到大排列得:,,,,,,,,,
故中位数为第五个数,故错误;
这9年我国快递业务量同比增速的极差为,故错误;
由条形图可得,自2016年起,各年的快递业务量远超过210亿件,故快递业务量的平均数超过210亿件,故正确.
故选:.
5.解:甲的成绩分别为90,93,92,94,96,93,乙的成绩分别为93,94,91,95,92,93,
甲成绩的中位数为,乙成绩的中位数为,错误,
甲成绩的众数为93,乙成绩的众数为93,错误,
甲成绩的极差为,乙成绩的极差为,错误,
甲成绩的平均数为,甲成绩的方差为,
乙成绩的平均数为,乙成绩的方差为,
,乙成绩比甲成绩稳定,正确.
故选:.
6.解:对于,由折线图知平均指数值不超过100,所以正确;
对于,通过折线图知平均指数均在50以下,说明至少有一天空气质量为优,所以正确;
对于,2月,8月,9月和12月的最大值指数有大于100,空气质量为“污染”,所以正确;
对于,根据折线图2月份出现最大值,并不表示空气质量为“污染”的天数最多的月份是2月份,所以错误;
故选:.
7.解:.根据中位数的定义可得:月跑步平均里程的中位数大于6月份对应的里程数,因此不正确.
.月跑步平均里程不是逐月增加,因此不正确;
.月跑步平均里程高峰期大致在10月,因此不正确.
月至5月的跑步平均里程相对于6月至11月,波动性更小,变化比较平稳,正确.
故选:.
8.解:因为,,
所以第30百分位数为,第50百分位数为,
解得,
所以.
故选:.
9.解:根据雷达图可看出,甲的数学运算素养为5分,乙的为4分,正确;
甲的逻辑推理素养为4分,乙的为5分,错误;
甲的六个核心素养中只有数学运算素养为5分,正确;
乙的六个核心素养中,有3个为5分,错误.
故选:.
10.解:根据题意,依次分析选项:
对于,由统计图可知,第2周增长数量比第1周增长数量明显要多,所以是加速增长,所以选项正确;
对于,当,时图象是线段,所以是匀速增长,所以选项正确;
对于,当,时增长数量比当,时增长数量要少,所以是减少,所以选项错误;
对于,当,时共增长2.4吨,当,时共增长0.6吨,所以减少了1.8吨,所以选项错误.
故选:.
11.解:对于,根据双层饼图得1季度和2季度的销售额和为万元,
1季度和2季度销售额占总销售额的百分比之和为:,
年的总销售额为:(万元),故正确;
对于,2月份销售额为:(万元),故错误;
对于,4季度销售额为(万元),故正确;
对于,根据双层饼图得12个月的销售额从小到大为(单位:万元),50,60,60,60,80,90,100,100,110,120,120,
个月的销售额的中位数为:(万元),故错误.
故选:.
12.解:对于,由频率分布直方图得考生竞赛成绩的众数为分,故正确;
对于,不及格的考生人数为:,故错误;
对于,考生竞赛成绩的平均数为:
分,故正确;
对于,,的频率为,
,的频率为,
考生竞赛成绩的中位数为:分,故错误.
故选:.
13.解:按分层抽样方法,抽取高中学生为(人,
初中学生为(人,
小学生为(人.
故答案为:24,109,110.
14.解:由频数分布表得,的频数为20,频率为0.4,
样本容量为,
,,
由频率分布直方图得,.
.
故答案为:50,1000.
15.解:甲实得分为80分,记为60分,少记20分,乙实得70分,记为90分,多记20分,
总分没有变化,更正前后的平均分没有变化,都是80分,
设甲乙以外的其他同学的成绩分别为,,,,
更正前的方差为70,
,
,
,
更正后的方差为:
,
更正后的方差为60.
故答案为:60.
16.解:样本容量为:;
抽取的高中生人数为:.
故答案为:300;30.
17解:(1)由频率分布直方图得:
,
解得.
(2)估计该校学生数学竞赛成绩的平均数为:
.
(3),的频率为,
,的频率为,
估计该校学生数学竞赛成绩的第80百分位数落在,内.
18.解:(1)由频率分布直方图得质量超过515克的产品的频率为:
,
估计这条生产流水线上,质量超过515克的产品的比例为.
(2)由频率分布直方图得:
.
方差.
一.单选题
1.从2019年末开始,新型冠状病毒在全球肆虐.为了研制新型冠状病毒疫苗,某大型药企需要从150名志愿者中抽取15名志愿者进行临床试验,现采用分层抽样的方法进行抽取,若这150名志愿者中老年人的人数为50人,则老年人中被抽到进行临床试验的人数是
A.15 B.10 C.5 D.1
2.某班60名同学中选出4人参加户外活动,利用随机数表法抽取样本时,先将60名同学按01,02,,60进行编号,然后从随机数表第1行的第5列和第6列数字开始从左往右依次选取两个数字,则选出的第4个同学的编号为
0347 4373 8636 9647 3661 4698 6371 6297
7424 6292 4281 1457 2042 5332 3732 1676
(注表中的数据为随机数表的第一行和第二行)
A.24 B.36 C.46 D.47
3.有17名同学参加百米竞赛,预赛成绩各不相同,要取前8名参加决赛,小明同学已经知道了自己的成绩,为了判断自己是否能进入决赛,他还需要知道17名同学成绩的
A.平均数 B.众数 C.中位数 D.方差
4.随着互联网和物流行业的快速发展,快递业务已经成为人们日常生活当中不可或缺的重要组成部分.如图是年我国快递业务量变化情况统计图,则关于这9年的统计信息,下列说法正确的是
A.这9年我国快递业务量有增有减
B.这9年我国快递业务量同比增速的中位数为
C.这9年我国快递业务量同比增速的极差未超过
D.这9年我国快递业务量的平均数超过210亿件
5.第31届世界大学生夏季运动会将于2021年8月在成都举行,举办方将招募志愿者在赛事期间为运动会提供咨询、交通引导、场馆周边秩序维护等服务.招募的志愿者需接受专业培训,甲、乙两名志愿者在培训过程中进行了六次测试,其测试成绩(单位:分)如折线图所示,则下列说法正确的是
A.甲成绩的中位数比乙成绩的中位数大
B.甲成绩的众数比乙成绩的众数小
C.甲成绩的极差比乙成绩的极差小
D.乙的成绩比甲的成绩稳定
6.空气质量的指数是反映空气质量状况的指数,指数的值越小,表明空气质量越好.指数不超过50,空气质量为“优”; 指数大于50,且不超过100,空气质量为“良”; 指数大于100,空气质量为“污染”.如图是某市2020年空气质量指数的月折线图.下列关于该市2020年空气质量的叙述中不一定正确的
A.全年的平均指数对应的空气质量等级为优或良
B.每月都至少有一天空气质量为优
C.2月,8月,9月和12月均出现污染天气
D.空气质量为“污染”的天数最多的月份是2月份
7.某学校为了解学校学生组成的跑步社团每月跑步的平均里程,收集并整理了2020年1月至2020年12月期间跑步社团的成员每月跑步的平均里程(单位:公里)的数据,绘制了下面的折线图:
根据折线图,下列结论正确的是
A.月跑步平均里程的中位数为6月份对应的平均里程
B.月跑步平均里程逐月增加
C.月跑步平均里程高峰期大致在8、9月
D.1月至6月的月跑步平均里程相对于7月至12月,波动性更小,变化比较平稳
8.已知甲、乙两组是按大小顺序排列的数据.甲组:27,28,37,,40,50;乙组:24,,34,43,48,52.若这两组数据的第30百分位数、第50百分位数分别对应相等,则等于
A. B. C. D.
二.多选题
9.《高中数学课程标准》版)给出了数学学科的六大核心素养,为了比较甲乙两名高中学生的数学核心素养水平,现以六大素养为指标对二人进行了测验,根据测验结果绘制了雷达图,图中每项指标值满分为5分,分值高者为优,则下列说法正确的是
A.甲的数学运算素养优于乙的数学运算素养
B.甲的逻辑推理素养优于乙的逻辑推理素养
C.甲的六个核心素养中只有数学运算水平最高
D.乙的六个核心素养中只有数据分析水平最高
10.为了了解市民对各种垃圾进行分类的情况,加强垃圾分类宣传的针对性,指导市民尽快掌握垃圾分类的方法,某市垃圾处理厂连续8周对有害垃圾错误分类情况进行了调查.经整理绘制了如图所示的有害垃圾错误分类重量累积统计图,图中横轴表示时间(单位:周),纵轴表示有害垃圾错误分类的累积重量(单位:吨).根据统计图分析,下列结论正确的是
A.当,时有害垃圾错误分类的重量加速增长
B.当,时有害垃圾错误分类的重量匀速增长
C.当,时有害垃圾错误分类的重量相对于当,时增长了
D.当,时有害垃圾错误分类的重量相对于当,时减少了0.6吨
11.某网络销售平台,实施对口扶贫,销售某县扶贫农产品.根据2020年全年该县扶贫农产品的销售额(单位:万元)和扶贫农产品销售额占总销售额的百分比,绘制了如图的双层饼图.根据双层饼图(季度和月份后面标注的是销售额或销售额占总销售额的百分比),下列说法正确的是
A.2020年的总销售额为1000万元
B.2月份的销售额为8万元
C.4季度销售额为280万元
D.12个月的销售额的中位数为90万元
12.在疫情防护知识竞赛中,对某校的2000名考生的参赛成绩进行统计,可得到如图所示的频率分布直方图,其中分组的区间为,,,,,,,,,,,,60分以下视为不及格,若同一组中数据用该组区间中间值作代表值,则下列说法中正确的是
A.考生竞赛成绩的众数为75分
B.不及格的考生人数为500
C.考生竞赛成绩的平均数为72.5分
D.考生竞赛成绩的中位数为75分
三.填空题
13.某地区有高中学生2400人,初中学生10900人,小学生11000人,此地教育局为了了解本地区中小学生的近视情况及其形成原因,要从本地区抽取的学生进行调查,则按分层抽样的方法抽取高中学生,初中学生和小学生的人数分别是 , , .
14.某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.若下面是尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示),则样本容量为 ,的值为 .
组别 分组 频数 频率
第1组 , 8 0.16
第2组 ,
▓
第3组 , 20 0.40
第4组 , ▓ 0.08
第5组 , 2
合计 ▓ ▓
15.某班40名学生,在一次考试中统计所得平均分为80分,方差为70,后来发现有两名同学的成绩有误,甲实得80分错记为60分,乙实得70分错记为90分,则更正后的方差为 .
16.已知某地区中小学生人数和近视情况分别如图甲和乙所示.为了了解该地区中小学生的近视形成原因,用分层抽样的方法抽取的学生进行调查,则样本容量为 ;抽取的高中生中近视的人数为 .
四.解答题
17.某校对120名考生的数学竞赛成绩进行统计,分成,,,,,,,,,五组,得到如图所示频率分布直方图.
(1)求图中的值;
(2)估计该校学生数学竞赛成绩的平均数;
(3)估计该校学生数学竞赛成绩的第80百分位数落在哪一组.
18.某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的100件产品作为样本称出它们的质量(单位:克),质量的分组区间为,,,,,,,由此得到样本的频率分布直方图如图所示.
(1)估计这条生产流水线上,质量超过515克的产品的比例;
(2)求这条生产流水线上产品质量的平均数和方差的估计值(同一组中的数据用该组区间的中点值作代表).
第九章专题训练—统计 答案
1.解:某大型药企需要从150名志愿者中抽取15名志愿者进行临床试验,
现采用分层抽样的方法进行抽取,
若这150名志愿者中老年人的人数为50人,
则老年人中被抽到进行临床试验的人数是:.
故选:.
2.解:由题知从随机数表的第1行第5列和第6列数字开始,
由表可知依次选取43,36,47,46,24.
故选:.
3.解:因为共有17个人,且他们的分数各不相同,第9名的成绩是中位数,
故要判断是否能进入决赛,他还需要知道17名同学成绩的中位数.
故选:.
4.解:由条形图可得,这9年我国快递业务量逐年增加,故错误;
将各年我国快递业务量同比增速按从小到大排列得:,,,,,,,,,
故中位数为第五个数,故错误;
这9年我国快递业务量同比增速的极差为,故错误;
由条形图可得,自2016年起,各年的快递业务量远超过210亿件,故快递业务量的平均数超过210亿件,故正确.
故选:.
5.解:甲的成绩分别为90,93,92,94,96,93,乙的成绩分别为93,94,91,95,92,93,
甲成绩的中位数为,乙成绩的中位数为,错误,
甲成绩的众数为93,乙成绩的众数为93,错误,
甲成绩的极差为,乙成绩的极差为,错误,
甲成绩的平均数为,甲成绩的方差为,
乙成绩的平均数为,乙成绩的方差为,
,乙成绩比甲成绩稳定,正确.
故选:.
6.解:对于,由折线图知平均指数值不超过100,所以正确;
对于,通过折线图知平均指数均在50以下,说明至少有一天空气质量为优,所以正确;
对于,2月,8月,9月和12月的最大值指数有大于100,空气质量为“污染”,所以正确;
对于,根据折线图2月份出现最大值,并不表示空气质量为“污染”的天数最多的月份是2月份,所以错误;
故选:.
7.解:.根据中位数的定义可得:月跑步平均里程的中位数大于6月份对应的里程数,因此不正确.
.月跑步平均里程不是逐月增加,因此不正确;
.月跑步平均里程高峰期大致在10月,因此不正确.
月至5月的跑步平均里程相对于6月至11月,波动性更小,变化比较平稳,正确.
故选:.
8.解:因为,,
所以第30百分位数为,第50百分位数为,
解得,
所以.
故选:.
9.解:根据雷达图可看出,甲的数学运算素养为5分,乙的为4分,正确;
甲的逻辑推理素养为4分,乙的为5分,错误;
甲的六个核心素养中只有数学运算素养为5分,正确;
乙的六个核心素养中,有3个为5分,错误.
故选:.
10.解:根据题意,依次分析选项:
对于,由统计图可知,第2周增长数量比第1周增长数量明显要多,所以是加速增长,所以选项正确;
对于,当,时图象是线段,所以是匀速增长,所以选项正确;
对于,当,时增长数量比当,时增长数量要少,所以是减少,所以选项错误;
对于,当,时共增长2.4吨,当,时共增长0.6吨,所以减少了1.8吨,所以选项错误.
故选:.
11.解:对于,根据双层饼图得1季度和2季度的销售额和为万元,
1季度和2季度销售额占总销售额的百分比之和为:,
年的总销售额为:(万元),故正确;
对于,2月份销售额为:(万元),故错误;
对于,4季度销售额为(万元),故正确;
对于,根据双层饼图得12个月的销售额从小到大为(单位:万元),50,60,60,60,80,90,100,100,110,120,120,
个月的销售额的中位数为:(万元),故错误.
故选:.
12.解:对于,由频率分布直方图得考生竞赛成绩的众数为分,故正确;
对于,不及格的考生人数为:,故错误;
对于,考生竞赛成绩的平均数为:
分,故正确;
对于,,的频率为,
,的频率为,
考生竞赛成绩的中位数为:分,故错误.
故选:.
13.解:按分层抽样方法,抽取高中学生为(人,
初中学生为(人,
小学生为(人.
故答案为:24,109,110.
14.解:由频数分布表得,的频数为20,频率为0.4,
样本容量为,
,,
由频率分布直方图得,.
.
故答案为:50,1000.
15.解:甲实得分为80分,记为60分,少记20分,乙实得70分,记为90分,多记20分,
总分没有变化,更正前后的平均分没有变化,都是80分,
设甲乙以外的其他同学的成绩分别为,,,,
更正前的方差为70,
,
,
,
更正后的方差为:
,
更正后的方差为60.
故答案为:60.
16.解:样本容量为:;
抽取的高中生人数为:.
故答案为:300;30.
17解:(1)由频率分布直方图得:
,
解得.
(2)估计该校学生数学竞赛成绩的平均数为:
.
(3),的频率为,
,的频率为,
估计该校学生数学竞赛成绩的第80百分位数落在,内.
18.解:(1)由频率分布直方图得质量超过515克的产品的频率为:
,
估计这条生产流水线上,质量超过515克的产品的比例为.
(2)由频率分布直方图得:
.
方差.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
