正方形
图片预览





文档简介
(共22张PPT)
比较平行四边形与矩形和菱形的性质
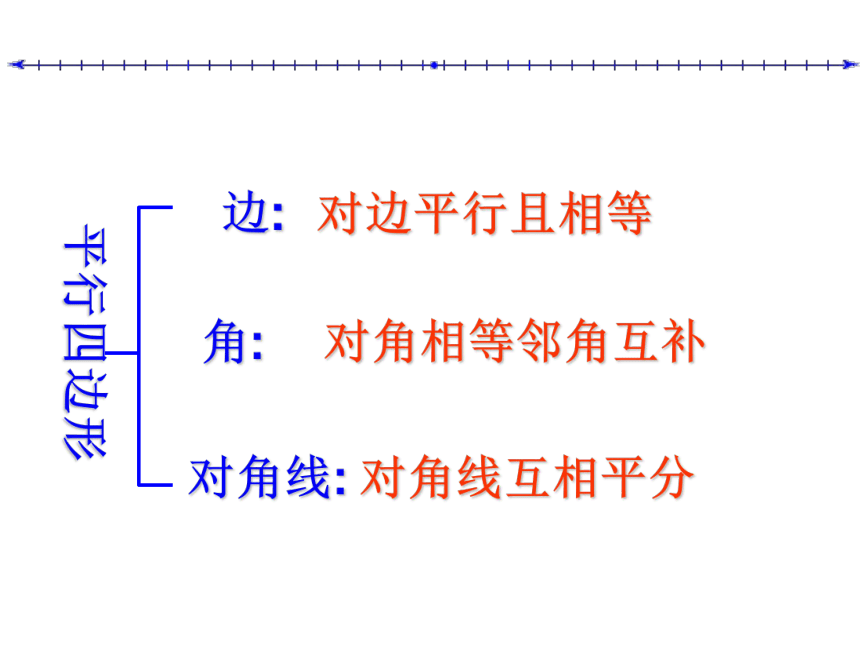
平行四边形
对边平行且相等
对角相等邻角互补
对角线互相平分
边:
角:
对角线:
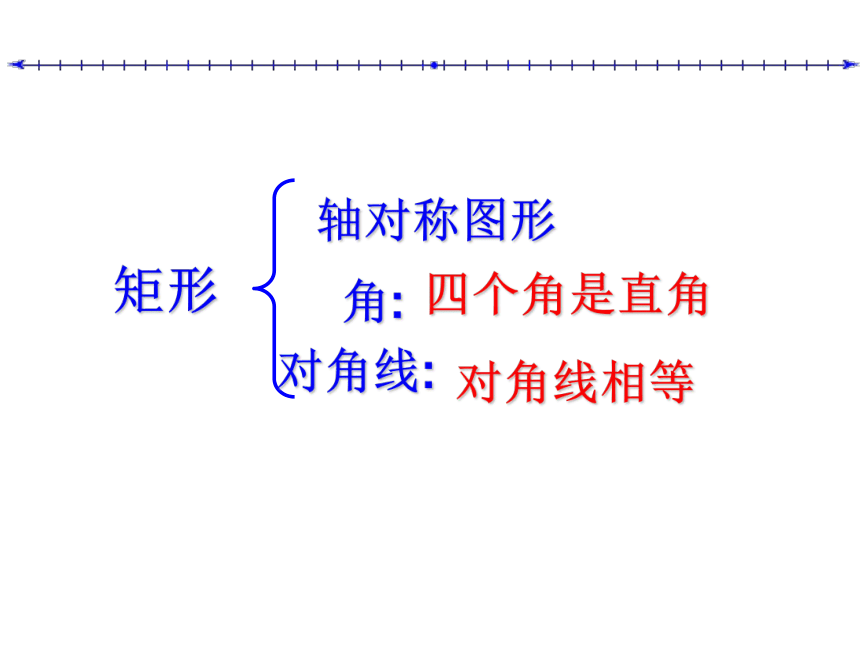
矩形
角:
对角线:
轴对称图形
四个角是直角
对角线相等
菱形的性质
菱
形
的
性
质
边:
四条边相等
对角线:
互相垂直
分别平分两组对角
轴对称图形
具有平行四边形一切性质
探索:什么样的图形是正方形 正方形 是菱形吗 为什么 正方形是矩形吗 为什么 正方形具有怎样的性质
对称性
特征
正方形是中心对称图形
它也是轴对称图形
(1)它具有平行四边形的一切性质
两组对边分别平行且相等,两组对角相等,对角线互相平分
(2)具有矩形的一切性质
四个角都是直角,对角线相等
(3)具有菱形的一切性质
四条边相等;对角线互相垂直,每条对角线平分一组对角
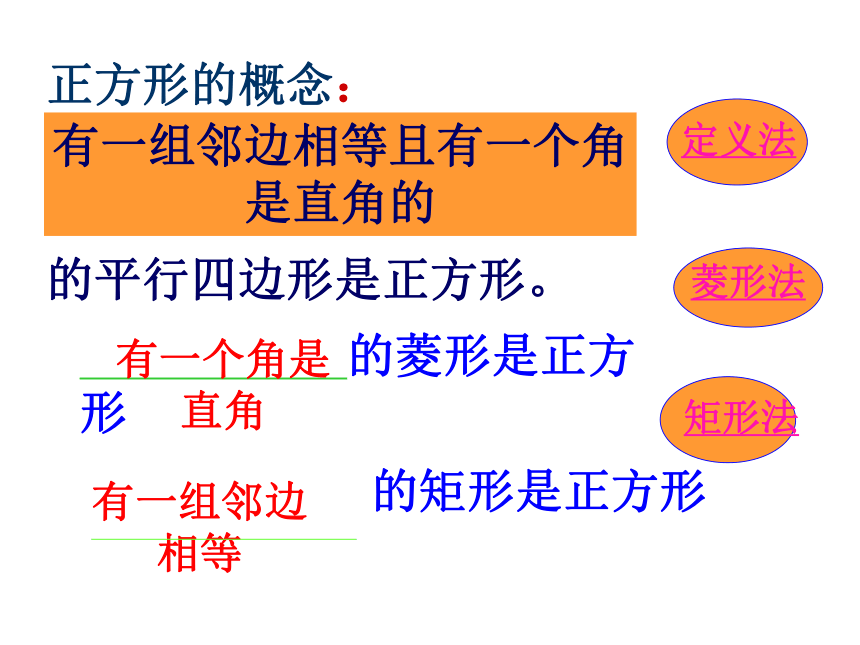
正方形的概念:
的平行四边形是正方形。
的菱形是正方形
的矩形是正方形
定义法
菱形法
矩形法
有一组邻边相等且有一个角
是直角的
有一个角是直角
有一组邻边相等
平行四边形
正方形
矩形
菱形
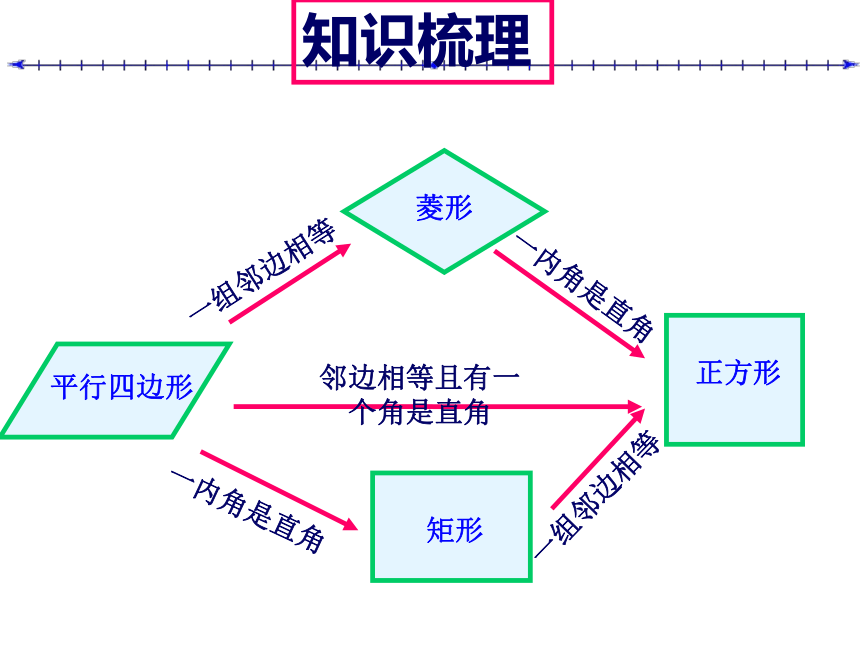
一组邻边相等
一组邻边相等
一内角是直角
一内角是直角
邻边相等且有一个角是直角
知识梳理
平行四边形、矩形、菱形、正方形之间关系
平行四边形
矩形
菱形
正方形
平行四边形、矩形、菱形、正方形之间关系
例题解析
学一学
例1. 如图12.2.8,在正方ABCD中,求∠ABD、∠DAC、∠DOC的度数。
解:
因为四边形ABCD是正方形
得
根据正方形的四个内角都为直角
又因为正方形的对角线平分内角
所以
根据正方形的两条对角线互相垂直
所以
例2.如图四边形ABCD和DEFG都是正方形,
试说明AE=CG
A
B
C
D
E
F
G
解:
因为四边形ABCD是正方形
根据正方形的四边相等,得
AD=CD
又知四边形DEFG也是正方形
所以 DE=DG
又因为正方形的每个内角为
所以
所以
所以三角形ADE可以看成是由三角形CDG绕着点D顺时针
旋转 得到。
所以AE=CG
范例精讲:
例1 求证:正方形的两条对角线把正方形
分成四个全等的等腰直角三角形。
求证: △AOB 、△BOC 、 △COD、
△AOD是全等的等腰直角三角形
已知:如图,正方形ABCD的对角线AC、BD
相交 于点O.
思考:要从几个方面去证明这个问题
证明:
∵四边形ABCD是正方形
∴AC=BD,AC⊥BD
AO=BO=CO=DO
∴△AOB、 △BOC 、△COD、
△AOD 是等腰直角三角形,并且
△AOB ≌△BOC ≌△COD ≌△AOD
练习1.
已知: 正方形ABCD对角线 AC、
BD相交于点O且AB=a cm
求:AC的长及正方形的面积S。
(2)△ABC是什么三角形?
(1)正方形的面积怎么求?
分析:
若正方形的边长a cm,则该正方形的对角线长为 cm
结论:
边长乘以边长
直角三角形
(3)知道直角三角形两直角边的长,
要求斜边的长该么办
应用勾股定理
练习2.
已知:在正方形ABCD中,
对角线AC、BD相交
于点O,且AC=6cm,
求: 正方形的面积S。
分析:
解法一:先求△AOB的面积,正方形的面积是△AOB
面积的几倍?
解法二:正方形的边长和对角线的长有什么关系?
解法三: 正方形是特殊的菱形,菱形的面积怎么求?
请大家自己完成练习!
例2
已知:如图(4)在正方形ABCD中,F为CD延长
线上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45°
分析:欲证∠MFD=45°,由于△MDF是直角三角形,
只须证△MDF是等腰三角形,
即只要证 _____=_____
要证MD=FD,大家只须证得哪两个三角形全等
△CMD≌△ADF
试一试看能不能完成证明
证明:
∵四边形ABCD是正方形
∴CD=AD ∠CDA=∠ADF=90°
∵∠CMD与∠AME是对顶角
∴∠CMD=∠AME
∵CE⊥AF
∴∠AEM=90°
∴∠1=∠2
在△CMD和△AFD中
∠1=∠2
CD=AD
∠CDA=∠ADF=90°
∴ △CMD≌△AFD (ASA)
∴DM=DF
∴∠MFD=45°
请你谈谈本节课有哪些收获
感悟与收获
归纳
1 、正方形是中心对称图形,轴对称图形。
2、正方形的四条边都相等。
3、正方形的四个角都相等。
4、正方形的对角线互相垂直平分且相等,
且每一条对角线平分一组对角。
A
B
C
D
比较平行四边形与矩形和菱形的性质
平行四边形
对边平行且相等
对角相等邻角互补
对角线互相平分
边:
角:
对角线:
矩形
角:
对角线:
轴对称图形
四个角是直角
对角线相等
菱形的性质
菱
形
的
性
质
边:
四条边相等
对角线:
互相垂直
分别平分两组对角
轴对称图形
具有平行四边形一切性质
探索:什么样的图形是正方形 正方形 是菱形吗 为什么 正方形是矩形吗 为什么 正方形具有怎样的性质
对称性
特征
正方形是中心对称图形
它也是轴对称图形
(1)它具有平行四边形的一切性质
两组对边分别平行且相等,两组对角相等,对角线互相平分
(2)具有矩形的一切性质
四个角都是直角,对角线相等
(3)具有菱形的一切性质
四条边相等;对角线互相垂直,每条对角线平分一组对角
正方形的概念:
的平行四边形是正方形。
的菱形是正方形
的矩形是正方形
定义法
菱形法
矩形法
有一组邻边相等且有一个角
是直角的
有一个角是直角
有一组邻边相等
平行四边形
正方形
矩形
菱形
一组邻边相等
一组邻边相等
一内角是直角
一内角是直角
邻边相等且有一个角是直角
知识梳理
平行四边形、矩形、菱形、正方形之间关系
平行四边形
矩形
菱形
正方形
平行四边形、矩形、菱形、正方形之间关系
例题解析
学一学
例1. 如图12.2.8,在正方ABCD中,求∠ABD、∠DAC、∠DOC的度数。
解:
因为四边形ABCD是正方形
得
根据正方形的四个内角都为直角
又因为正方形的对角线平分内角
所以
根据正方形的两条对角线互相垂直
所以
例2.如图四边形ABCD和DEFG都是正方形,
试说明AE=CG
A
B
C
D
E
F
G
解:
因为四边形ABCD是正方形
根据正方形的四边相等,得
AD=CD
又知四边形DEFG也是正方形
所以 DE=DG
又因为正方形的每个内角为
所以
所以
所以三角形ADE可以看成是由三角形CDG绕着点D顺时针
旋转 得到。
所以AE=CG
范例精讲:
例1 求证:正方形的两条对角线把正方形
分成四个全等的等腰直角三角形。
求证: △AOB 、△BOC 、 △COD、
△AOD是全等的等腰直角三角形
已知:如图,正方形ABCD的对角线AC、BD
相交 于点O.
思考:要从几个方面去证明这个问题
证明:
∵四边形ABCD是正方形
∴AC=BD,AC⊥BD
AO=BO=CO=DO
∴△AOB、 △BOC 、△COD、
△AOD 是等腰直角三角形,并且
△AOB ≌△BOC ≌△COD ≌△AOD
练习1.
已知: 正方形ABCD对角线 AC、
BD相交于点O且AB=a cm
求:AC的长及正方形的面积S。
(2)△ABC是什么三角形?
(1)正方形的面积怎么求?
分析:
若正方形的边长a cm,则该正方形的对角线长为 cm
结论:
边长乘以边长
直角三角形
(3)知道直角三角形两直角边的长,
要求斜边的长该么办
应用勾股定理
练习2.
已知:在正方形ABCD中,
对角线AC、BD相交
于点O,且AC=6cm,
求: 正方形的面积S。
分析:
解法一:先求△AOB的面积,正方形的面积是△AOB
面积的几倍?
解法二:正方形的边长和对角线的长有什么关系?
解法三: 正方形是特殊的菱形,菱形的面积怎么求?
请大家自己完成练习!
例2
已知:如图(4)在正方形ABCD中,F为CD延长
线上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45°
分析:欲证∠MFD=45°,由于△MDF是直角三角形,
只须证△MDF是等腰三角形,
即只要证 _____=_____
要证MD=FD,大家只须证得哪两个三角形全等
△CMD≌△ADF
试一试看能不能完成证明
证明:
∵四边形ABCD是正方形
∴CD=AD ∠CDA=∠ADF=90°
∵∠CMD与∠AME是对顶角
∴∠CMD=∠AME
∵CE⊥AF
∴∠AEM=90°
∴∠1=∠2
在△CMD和△AFD中
∠1=∠2
CD=AD
∠CDA=∠ADF=90°
∴ △CMD≌△AFD (ASA)
∴DM=DF
∴∠MFD=45°
请你谈谈本节课有哪些收获
感悟与收获
归纳
1 、正方形是中心对称图形,轴对称图形。
2、正方形的四条边都相等。
3、正方形的四个角都相等。
4、正方形的对角线互相垂直平分且相等,
且每一条对角线平分一组对角。
A
B
C
D
