7.3 离散型随机变量的数字特征 (专项训练)-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(Word版含解析)
文档属性
| 名称 | 7.3 离散型随机变量的数字特征 (专项训练)-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 754.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 20:04:01 | ||
图片预览




文档简介
2020—2021学年高二数学下学期
7.3离散型随机变量的数字特征
专项训练
一、单选题(共12题;共60分)
1.随机变量false的分布列是( )
false
2
4
6
false
false
false
false
A.false B.false
C.false D.false
2.广雅高一年级和高二年级进行篮球比赛,赛制为3局2胜制,若比赛没有平局,且高二队每局获胜的概率都是false,记比赛的最终局数为随机变量false,则()
A.false B.false C.false D.false
3.已知集合false,false,从集合false中任取3个不同的元素,其中最小的元素用false表示,从集合false中任取3个不同的元素,其中最大的元素用false表示,记false,则随机变量false的期望为( )
A.false B.false C.3 D.4
4.已知正整数false,false,随机变量false的分布列是
false
false
false
false
false
false
false
false
false
false
false
false
false
false
则当false在false内增大时,( )
A.false B.false
C.false D.E(X)与false没有确定的大小关系
5.设false、false、false,已知随机变量false的分布列为:
false
false
false
false
false
false
false
false
且false,则false的最小值为( )
A.false B.false C.false D.false
6.已知某口袋中有2个白球和2个黑球,若从中随机取出1个球,再放回1个不同颜色的球,此时袋中的白球个数为false;若从中随机取出2个球,再放回2个不同颜色的球(若取出的是1个黑球1个白球,则放回1个白球1个黑球),此时袋中的白球个数为false,则( )
A.false B.false
C.false D.false
7.已知随机变量X,Y的分布列如下:
X
0
1
2
P
false
a
b
Y
false
false
P
false
m
则false的最小值为( )
A.1 B.false C.2 D.false
8.已知随机变量false的可能取值分别为-1,1,且false,false,其中false,下列关于false,false的说法正确的是( )
A.false,false均随x的增大而减小
B.false随x的增大而减小,false随x的增大而增大
C.false为定值,false随x的增大而减小
D.false随x的增大而减小,false为定值
9.已知随机变量false的分布列如下:
false
false
false
false
false
false
false
false
则false最大值( )
A.false B.false C.false D.不是定值
10.已知甲盒中有2个红球,1个蓝球,乙盒中有1个红球,2个篮球,从甲乙两个盒中各取1球放入原来为空的丙盒中,现从甲盒中取1个球,记红球的个数为false,从乙盒中取1个球,记红球的个数为false,从丙盒中取1个球,记红球的个数为false,则下列说法正确的是
A.false
B.false
C.false
D.false
11.已知随机变量false满足false, false, false,若false,则
A.false随着false的增大而增大, false随着false的增大而增大
B.false随着false的增大而减小, false随着false的增大而增大
C.false随着false的增大而减小, false随着false的增大而减小
D.false随着false的增大而增大, false随着false的增大而减小
12.下列关于正态分布false的命题:
①正态曲线关于false轴对称;
②当false一定时,false越大,正态曲线越“矮胖”,false越小,正态曲线越“瘦高”;
③设随机变量false,则false的值等于2;
④当false一定时,正态曲线的位置由false确定,随着false的变化曲线沿false轴平移.
其中正确的是
A.①② B.③④ C.②④ D.①④
二、填空题(共4题;共20分)
13.连续投掷一枚均匀硬币,正面出现false次或者背面只要出现一次,就算比赛结束,则比赛结束时出现正面的次数的数学期望是_____________.
14.已知随机变量false的分布列如表所示:false
false
false
false
false
false
false
false
false
则false的最大值是___________.
15.已知随机变量false的概率分布为false,则false______.
16.以下false个命题中,所有正确命题的序号是______.
①已知复数false,则false;
②若false,则false
③一支运动队有男运动员false人,女运动员false人,用分层抽样的方法从全体运动员中抽取一个容量为false的样本,则样本中男运动员有false人;
④若离散型随机变量false的方差为false,则false.
三、解答题(共4题;共20分)
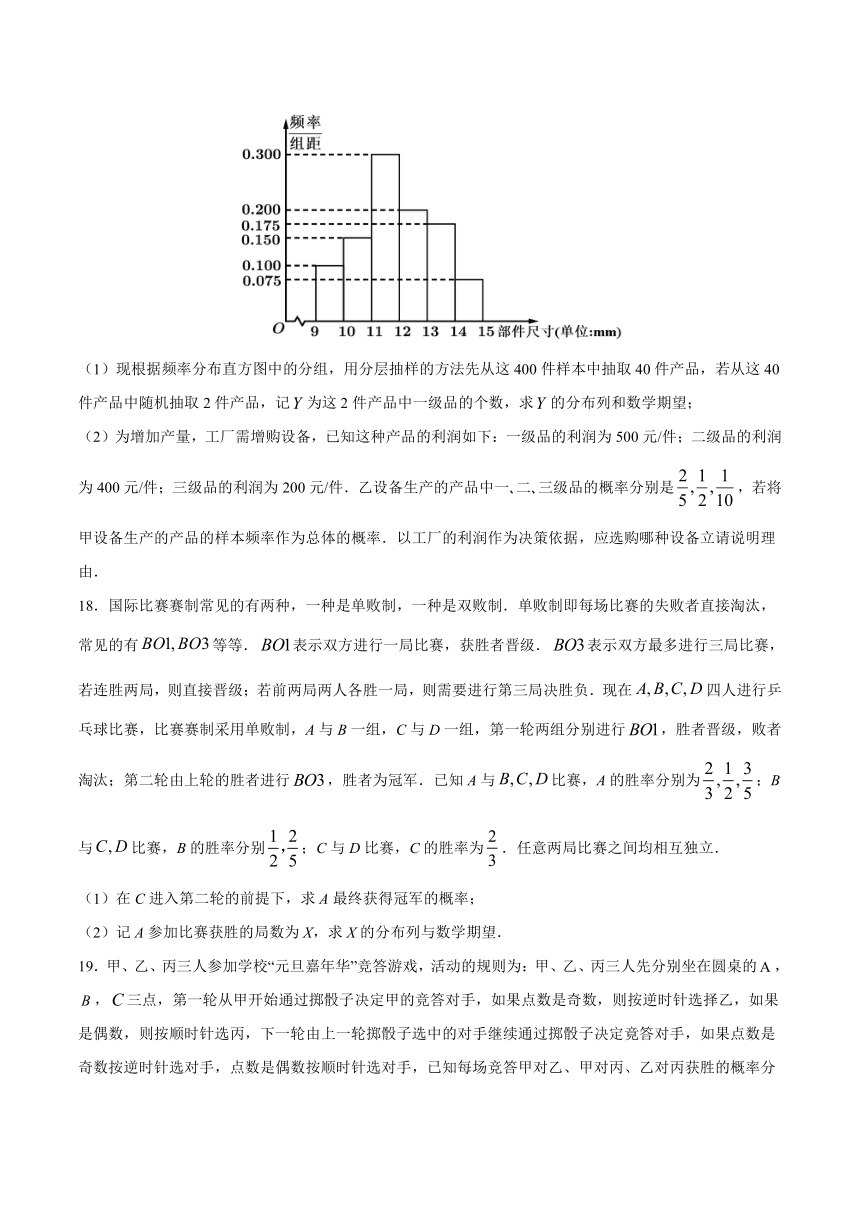
17.工厂经市场调研和科学研判,准备大规模生产某高科技产品的一个核心部件,目前只有某甲?乙两种设备可以独立生产该部件.如图是从甲设备生产的部件中随机抽取400件,对其核心部件的尺寸false(单位:false),进行统计整理的频率分布直方图.根据行业质量标准规定,该核心部件尺寸false满足:false为一级品,false为二级品,false为三级品
(1)现根据频率分布直方图中的分组,用分层抽样的方法先从这400件样本中抽取40件产品,若从这40件产品中随机抽取2件产品,记false为这2件产品中一级品的个数,求false的分布列和数学期望;
(2)为增加产量,工厂需增购设备,已知这种产品的利润如下:一级品的利润为500元/件;二级品的利润为400元/件;三级品的利润为200元/件.乙设备生产的产品中一?二?三级品的概率分别是false,若将甲设备生产的产品的样本频率作为总体的概率.以工厂的利润作为决策依据,应选购哪种设备立请说明理由.
18.国际比赛赛制常见的有两种,一种是单败制,一种是双败制.单败制即每场比赛的失败者直接淘汰,常见的有false等等.false表示双方进行一局比赛,获胜者晋级.false表示双方最多进行三局比赛,若连胜两局,则直接晋级;若前两局两人各胜一局,则需要进行第三局决胜负.现在false四人进行乒乓球比赛,比赛赛制采用单败制,A与B一组,C与D一组,第一轮两组分别进行false,胜者晋级,败者淘汰;第二轮由上轮的胜者进行false,胜者为冠军.已知A与false比赛,A的胜率分别为false;B与false比赛,B的胜率分别false;C与D比赛,C的胜率为false.任意两局比赛之间均相互独立.
(1)在C进入第二轮的前提下,求A最终获得冠军的概率;
(2)记A参加比赛获胜的局数为X,求X的分布列与数学期望.
19.甲、乙、丙三人参加学校“元旦嘉年华”竞答游戏,活动的规则为:甲、乙、丙三人先分别坐在圆桌的false,false,false三点,第一轮从甲开始通过掷骰子决定甲的竞答对手,如果点数是奇数,则按逆时针选择乙,如果是偶数,则按顺时针选丙,下一轮由上一轮掷骰子选中的对手继续通过掷骰子决定竟答对手,如果点数是奇数按逆时针选对手,点数是偶数按顺时针选对手,已知每场竞答甲对乙、甲对丙、乙对丙获胜的概率分别为false,false,false且甲、乙、丙之间竞答互不影响,各轮游戏亦互不影响,比赛中某选手累计获胜场数达到false场,游戏结束,该选手为晋级选手.
(1)求比赛进行了false场且甲晋级的概率;
(2)当比赛进行了false场后结束,记甲获胜的场数为false,求false的分布列与数学期望.
20.“博弈”原指下棋,出自我国《论语·阳货》篇,现在多指一种决策行为,即一些个人?团队或组织,在一定规则约束下,同时或先后,一次或多次,在各自允许选择的策略下进行选择和实施,并从中各自取得相应结果或收益的过程.生活中有很多游戏都蕴含着博弈,比如现在有两个人玩“亮”硬币的游戏,甲?乙约定若同时亮出正面,则甲付给乙3元,若同时亮出反面,则甲付给乙1元,若亮出结果是一正一反,则乙付给甲2元.
(1)若两人各自随机“亮”出正反面,求乙收益的期望.
(2)因为各自“亮”出正反面,而不是抛出正反面,所以可以控制“亮”出正面或反面的频率(假设进行多次游戏,频率可以代替概率),因此双方就面临竞争策略的博弈.甲?乙可以根据对手出正面的概率调整自己出正面的概率,进而增加自己赢得收益的期望,以收益的期望为决策依据,甲?乙各自应该如何选择“亮”出正面的概率,才能让结果对自己最有利?并分析游戏规则是否公平.
参考答案
1.A
【详解】
false,false
false
false
falsefalse故选:A
2.C
【详解】
false的可能取值为2,3,
解法一:false,
false,
令false,因为false,所以false
则false;false
所以false,
false
false
false,
因为false,所以false,
false
法二:false,
false,
false,
因为false以false为对称轴,开口向下,
所以false在false时,false单调递增,
所以false,排除A,B.
法1:false
false
false
false
令false,false
法2:false
false
false
false
false,false
所以false在false上单调递减,又false,
所以当false时,false,
所以false时false单调递增,
所以false.
故选:C
3.A
【详解】
根据题意,从集合false中任取3个不同的元素,则有false,其中最小的元素false取值分别为false,
从集合false中任取3个不同的元素,其中最大的元素false的取值分别为false,
因为false,可得随机变量false的取值为false,
则false,
false,
所以随机变量false的期望为:false.
故选:A.
4.A
【详解】
由条件可知false,
false,
false,false,false,即false.
故选:A
5.C
【详解】
由分布列得false,
则false,
当且仅当false,false时等号成立,所以false的最小值为false,
故选:C.
6.B
【详解】
由题意得false的可能取值为1,3,且false,
则false,false,
false的可能取值为0,2,4,
且false,false,
则falsefalse,false,
所以false,
故选:B
7.D
【详解】
解:由分布列的性质知,false,false,所以false,false,所以
false,false,
所以false,
当且仅当false,即false时等号成立,故false的最小值为false.
故选:D
8.B
【详解】
由题意知,随机变量false的数学期望false,
方差false.
当false时,false,由false在false恒成立.
所以false在false上单调递减,
false在false恒成立.
false在false上单调递增,
故选:B.
9.B
【详解】
由随机变量false的分布列得:
false,解得false,false,
false,false.
false,
当false时,false取得最大值false.
故选:false.
10.C
【详解】
随机变量false可取值false,其中
false,false,
故false,false.
随机变量false可取值false, false,false,
故false,false.
随机变量false可取值false,当false时,丙盒中无红球或有一个红球,
无红球的概率为false,有一个红球的概率为false,
故false,false,
故false,false.
综上,false,故选C.
11.C
【详解】
∵ 随机变量false满足false, false, false
∴false
∴false
∵false
∴false随着false的增大而减小, false随着false的增大而减小
故选C
12.C
【详解】
分析:根据正态分布的定义,及正态分布与各参数的关系结合正态曲线的对称性,逐一分析四个命题的真假,可得答案.
详解:①正态曲线关于false轴对称,故①不正确,
②当false一定时,false越大,正态曲线越“矮胖”,false越小,正态曲线越“瘦高”;正确;
③设随机变量false,则false的值等于1;故③不正确;
④当false一定时,正态曲线的位置由false确定,随着false的变化曲线沿false轴平移.正确.
故选C.
13.false
【详解】
由题意知:每次投掷硬币正面、背面出现的概率均为false;
∵正面出现false次或者背面只要出现一次,比赛结束,
∴假设比赛结束时,硬币抛掷了false次,false;
1、当false时,有前false次全部为正面,第false次为背面,则false,出现正面的次数的期望为false,
2、当false时,false次全部为正面,则false,出现正面的次数的期望为false,
∴false
故答案为:false
14.false
【详解】
由题知false,解得false,
则false,
false,
从而false
false,,false,
所以当false时,false取得最大值,最大值为false.
故答案为:false.
15.false
【详解】
因为false,
所以false,
解得false,
所以false,false,false,
所以false,
false.
故答案为:false
16.①③④
【详解】
①false,则false,①正确;
②令false,则false;令false,则false
false,②错误;
③抽样比为:false,则男运动员应抽取:false人,③正确;
④由方差的性质可知:false,④正确.
本题正确结果:①③④
17.(1)分布列见解析,期望为1(2)应选乙设备,理由见解析.
【详解】
(1)根据频率分布直方图中的分组,用分层抽样的分法抽取的40件产品中,
尺寸在false,false,false的产品数分别为false,false,
所以随机变量false的取值为false,
则false,false,false
所以随机变量false的分布列为:
false
0
1
2
false
false
false
false
所以期望false.
(2)设甲乙设备生产该产品一件的平均利润false元、false元,
由频率分布直方图可知,甲设备生产一级品、二级品、三级品的概率分别为:
false,
所以false,
false
可得false,所以应选购乙设备.
18.(1)false;(2)分布列见解析,false.
【详解】
解:(1)false进入第二轮的概率为false,
false与false比赛,false获胜,false与false比赛,false获胜,且false与false比赛,false获胜,
其概率为false,
故在false进入第二轮的前提下,false最终获得冠军的概率false.
(2)false参加比赛获胜的局数false的取值有0,1,2,3.
false,
false,
false,
false.
false的分布列为:
false
0
1
2
3
false
false
false
false
false
false.
19.(1)false;(2)分布列见解析;期望为false.
【详解】
解:(1)甲赢两场,分下面三种情况
①第一场甲胜,第二场无甲,第三场甲胜
概率为:false ;
②第一场甲输,二三场均胜
概率为:false;
③第一场甲胜,第二场输,第三场胜
概率为:false ;
由互斥事件的概率加法公式可知:比赛进行了false场且甲晋级的概率为:false.
(2)依题意false的所有可能取值为false,false,false
由(1)知false,
当比赛进行了false场后结束,甲获胜的场数为false时,
分两种情况:
3场比赛中甲参加了1场,输了,概率为:false
3场比赛中甲参加了2场,都输了,概率为:false
3场比赛甲都参加且都输掉是不可能的,否则两场比赛打不到3场.
所以false,
故false,
故false的分布列为
false
false
false
false
false
false
false
false
则false.
20.(1)false;(2)答案见解析.
【详解】
解析(1)因为是各自随机“亮”出正反面,所以甲?乙“亮”出正面的概率均可认为是false,
设乙在此游戏中的收益为随机变量false,则false的可能取值为false,1,3,
所以可得乙的收益的分布列为
false
-2
1
3
false
false
false
false
false.
(2)假设甲以false的概率“亮”出正面,乙以false的概率“亮”出正面,
甲收益的随机变量为false,乙收益的随机变量为false,此时甲的收益分布列为
false
2
-1
-3
false
false
false
false
所以甲的收益期望为falsefalse.
同理可得乙的收益分布列为
false
-2
1
3
false
false
false
false
所以乙的收益期望为falsefalse.
根据甲的收益期望,可知乙的最优策略是“亮”出正面的概率为false,
否则若false,有false,甲的收益期望false,
甲可以选择都“亮”出反面的策略,即false,达到预期收益最大,此时false.
若false,则甲选择都“亮”出正面的策略,即false,达到预期收益最大,false.
同理,可知甲的最优策略是“亮”出正面的概率为false,
所以最终两人的决策为保持“亮”出正面的概率都为false.
而当false时,false,false,
所以此时游戏结果对两人都是最有利,但是规则不公平.
7.3离散型随机变量的数字特征
专项训练
一、单选题(共12题;共60分)
1.随机变量false的分布列是( )
false
2
4
6
false
false
false
false
A.false B.false
C.false D.false
2.广雅高一年级和高二年级进行篮球比赛,赛制为3局2胜制,若比赛没有平局,且高二队每局获胜的概率都是false,记比赛的最终局数为随机变量false,则()
A.false B.false C.false D.false
3.已知集合false,false,从集合false中任取3个不同的元素,其中最小的元素用false表示,从集合false中任取3个不同的元素,其中最大的元素用false表示,记false,则随机变量false的期望为( )
A.false B.false C.3 D.4
4.已知正整数false,false,随机变量false的分布列是
false
false
false
false
false
false
false
false
false
false
false
false
false
false
则当false在false内增大时,( )
A.false B.false
C.false D.E(X)与false没有确定的大小关系
5.设false、false、false,已知随机变量false的分布列为:
false
false
false
false
false
false
false
false
且false,则false的最小值为( )
A.false B.false C.false D.false
6.已知某口袋中有2个白球和2个黑球,若从中随机取出1个球,再放回1个不同颜色的球,此时袋中的白球个数为false;若从中随机取出2个球,再放回2个不同颜色的球(若取出的是1个黑球1个白球,则放回1个白球1个黑球),此时袋中的白球个数为false,则( )
A.false B.false
C.false D.false
7.已知随机变量X,Y的分布列如下:
X
0
1
2
P
false
a
b
Y
false
false
P
false
m
则false的最小值为( )
A.1 B.false C.2 D.false
8.已知随机变量false的可能取值分别为-1,1,且false,false,其中false,下列关于false,false的说法正确的是( )
A.false,false均随x的增大而减小
B.false随x的增大而减小,false随x的增大而增大
C.false为定值,false随x的增大而减小
D.false随x的增大而减小,false为定值
9.已知随机变量false的分布列如下:
false
false
false
false
false
false
false
false
则false最大值( )
A.false B.false C.false D.不是定值
10.已知甲盒中有2个红球,1个蓝球,乙盒中有1个红球,2个篮球,从甲乙两个盒中各取1球放入原来为空的丙盒中,现从甲盒中取1个球,记红球的个数为false,从乙盒中取1个球,记红球的个数为false,从丙盒中取1个球,记红球的个数为false,则下列说法正确的是
A.false
B.false
C.false
D.false
11.已知随机变量false满足false, false, false,若false,则
A.false随着false的增大而增大, false随着false的增大而增大
B.false随着false的增大而减小, false随着false的增大而增大
C.false随着false的增大而减小, false随着false的增大而减小
D.false随着false的增大而增大, false随着false的增大而减小
12.下列关于正态分布false的命题:
①正态曲线关于false轴对称;
②当false一定时,false越大,正态曲线越“矮胖”,false越小,正态曲线越“瘦高”;
③设随机变量false,则false的值等于2;
④当false一定时,正态曲线的位置由false确定,随着false的变化曲线沿false轴平移.
其中正确的是
A.①② B.③④ C.②④ D.①④
二、填空题(共4题;共20分)
13.连续投掷一枚均匀硬币,正面出现false次或者背面只要出现一次,就算比赛结束,则比赛结束时出现正面的次数的数学期望是_____________.
14.已知随机变量false的分布列如表所示:false
false
false
false
false
false
false
false
false
则false的最大值是___________.
15.已知随机变量false的概率分布为false,则false______.
16.以下false个命题中,所有正确命题的序号是______.
①已知复数false,则false;
②若false,则false
③一支运动队有男运动员false人,女运动员false人,用分层抽样的方法从全体运动员中抽取一个容量为false的样本,则样本中男运动员有false人;
④若离散型随机变量false的方差为false,则false.
三、解答题(共4题;共20分)
17.工厂经市场调研和科学研判,准备大规模生产某高科技产品的一个核心部件,目前只有某甲?乙两种设备可以独立生产该部件.如图是从甲设备生产的部件中随机抽取400件,对其核心部件的尺寸false(单位:false),进行统计整理的频率分布直方图.根据行业质量标准规定,该核心部件尺寸false满足:false为一级品,false为二级品,false为三级品
(1)现根据频率分布直方图中的分组,用分层抽样的方法先从这400件样本中抽取40件产品,若从这40件产品中随机抽取2件产品,记false为这2件产品中一级品的个数,求false的分布列和数学期望;
(2)为增加产量,工厂需增购设备,已知这种产品的利润如下:一级品的利润为500元/件;二级品的利润为400元/件;三级品的利润为200元/件.乙设备生产的产品中一?二?三级品的概率分别是false,若将甲设备生产的产品的样本频率作为总体的概率.以工厂的利润作为决策依据,应选购哪种设备立请说明理由.
18.国际比赛赛制常见的有两种,一种是单败制,一种是双败制.单败制即每场比赛的失败者直接淘汰,常见的有false等等.false表示双方进行一局比赛,获胜者晋级.false表示双方最多进行三局比赛,若连胜两局,则直接晋级;若前两局两人各胜一局,则需要进行第三局决胜负.现在false四人进行乒乓球比赛,比赛赛制采用单败制,A与B一组,C与D一组,第一轮两组分别进行false,胜者晋级,败者淘汰;第二轮由上轮的胜者进行false,胜者为冠军.已知A与false比赛,A的胜率分别为false;B与false比赛,B的胜率分别false;C与D比赛,C的胜率为false.任意两局比赛之间均相互独立.
(1)在C进入第二轮的前提下,求A最终获得冠军的概率;
(2)记A参加比赛获胜的局数为X,求X的分布列与数学期望.
19.甲、乙、丙三人参加学校“元旦嘉年华”竞答游戏,活动的规则为:甲、乙、丙三人先分别坐在圆桌的false,false,false三点,第一轮从甲开始通过掷骰子决定甲的竞答对手,如果点数是奇数,则按逆时针选择乙,如果是偶数,则按顺时针选丙,下一轮由上一轮掷骰子选中的对手继续通过掷骰子决定竟答对手,如果点数是奇数按逆时针选对手,点数是偶数按顺时针选对手,已知每场竞答甲对乙、甲对丙、乙对丙获胜的概率分别为false,false,false且甲、乙、丙之间竞答互不影响,各轮游戏亦互不影响,比赛中某选手累计获胜场数达到false场,游戏结束,该选手为晋级选手.
(1)求比赛进行了false场且甲晋级的概率;
(2)当比赛进行了false场后结束,记甲获胜的场数为false,求false的分布列与数学期望.
20.“博弈”原指下棋,出自我国《论语·阳货》篇,现在多指一种决策行为,即一些个人?团队或组织,在一定规则约束下,同时或先后,一次或多次,在各自允许选择的策略下进行选择和实施,并从中各自取得相应结果或收益的过程.生活中有很多游戏都蕴含着博弈,比如现在有两个人玩“亮”硬币的游戏,甲?乙约定若同时亮出正面,则甲付给乙3元,若同时亮出反面,则甲付给乙1元,若亮出结果是一正一反,则乙付给甲2元.
(1)若两人各自随机“亮”出正反面,求乙收益的期望.
(2)因为各自“亮”出正反面,而不是抛出正反面,所以可以控制“亮”出正面或反面的频率(假设进行多次游戏,频率可以代替概率),因此双方就面临竞争策略的博弈.甲?乙可以根据对手出正面的概率调整自己出正面的概率,进而增加自己赢得收益的期望,以收益的期望为决策依据,甲?乙各自应该如何选择“亮”出正面的概率,才能让结果对自己最有利?并分析游戏规则是否公平.
参考答案
1.A
【详解】
false,false
false
false
falsefalse故选:A
2.C
【详解】
false的可能取值为2,3,
解法一:false,
false,
令false,因为false,所以false
则false;false
所以false,
false
false
false,
因为false,所以false,
false
法二:false,
false,
false,
因为false以false为对称轴,开口向下,
所以false在false时,false单调递增,
所以false,排除A,B.
法1:false
false
false
false
令false,false
法2:false
false
false
false
false,false
所以false在false上单调递减,又false,
所以当false时,false,
所以false时false单调递增,
所以false.
故选:C
3.A
【详解】
根据题意,从集合false中任取3个不同的元素,则有false,其中最小的元素false取值分别为false,
从集合false中任取3个不同的元素,其中最大的元素false的取值分别为false,
因为false,可得随机变量false的取值为false,
则false,
false,
所以随机变量false的期望为:false.
故选:A.
4.A
【详解】
由条件可知false,
false,
false,false,false,即false.
故选:A
5.C
【详解】
由分布列得false,
则false,
当且仅当false,false时等号成立,所以false的最小值为false,
故选:C.
6.B
【详解】
由题意得false的可能取值为1,3,且false,
则false,false,
false的可能取值为0,2,4,
且false,false,
则falsefalse,false,
所以false,
故选:B
7.D
【详解】
解:由分布列的性质知,false,false,所以false,false,所以
false,false,
所以false,
当且仅当false,即false时等号成立,故false的最小值为false.
故选:D
8.B
【详解】
由题意知,随机变量false的数学期望false,
方差false.
当false时,false,由false在false恒成立.
所以false在false上单调递减,
false在false恒成立.
false在false上单调递增,
故选:B.
9.B
【详解】
由随机变量false的分布列得:
false,解得false,false,
false,false.
false,
当false时,false取得最大值false.
故选:false.
10.C
【详解】
随机变量false可取值false,其中
false,false,
故false,false.
随机变量false可取值false, false,false,
故false,false.
随机变量false可取值false,当false时,丙盒中无红球或有一个红球,
无红球的概率为false,有一个红球的概率为false,
故false,false,
故false,false.
综上,false,故选C.
11.C
【详解】
∵ 随机变量false满足false, false, false
∴false
∴false
∵false
∴false随着false的增大而减小, false随着false的增大而减小
故选C
12.C
【详解】
分析:根据正态分布的定义,及正态分布与各参数的关系结合正态曲线的对称性,逐一分析四个命题的真假,可得答案.
详解:①正态曲线关于false轴对称,故①不正确,
②当false一定时,false越大,正态曲线越“矮胖”,false越小,正态曲线越“瘦高”;正确;
③设随机变量false,则false的值等于1;故③不正确;
④当false一定时,正态曲线的位置由false确定,随着false的变化曲线沿false轴平移.正确.
故选C.
13.false
【详解】
由题意知:每次投掷硬币正面、背面出现的概率均为false;
∵正面出现false次或者背面只要出现一次,比赛结束,
∴假设比赛结束时,硬币抛掷了false次,false;
1、当false时,有前false次全部为正面,第false次为背面,则false,出现正面的次数的期望为false,
2、当false时,false次全部为正面,则false,出现正面的次数的期望为false,
∴false
故答案为:false
14.false
【详解】
由题知false,解得false,
则false,
false,
从而false
false,,false,
所以当false时,false取得最大值,最大值为false.
故答案为:false.
15.false
【详解】
因为false,
所以false,
解得false,
所以false,false,false,
所以false,
false.
故答案为:false
16.①③④
【详解】
①false,则false,①正确;
②令false,则false;令false,则false
false,②错误;
③抽样比为:false,则男运动员应抽取:false人,③正确;
④由方差的性质可知:false,④正确.
本题正确结果:①③④
17.(1)分布列见解析,期望为1(2)应选乙设备,理由见解析.
【详解】
(1)根据频率分布直方图中的分组,用分层抽样的分法抽取的40件产品中,
尺寸在false,false,false的产品数分别为false,false,
所以随机变量false的取值为false,
则false,false,false
所以随机变量false的分布列为:
false
0
1
2
false
false
false
false
所以期望false.
(2)设甲乙设备生产该产品一件的平均利润false元、false元,
由频率分布直方图可知,甲设备生产一级品、二级品、三级品的概率分别为:
false,
所以false,
false
可得false,所以应选购乙设备.
18.(1)false;(2)分布列见解析,false.
【详解】
解:(1)false进入第二轮的概率为false,
false与false比赛,false获胜,false与false比赛,false获胜,且false与false比赛,false获胜,
其概率为false,
故在false进入第二轮的前提下,false最终获得冠军的概率false.
(2)false参加比赛获胜的局数false的取值有0,1,2,3.
false,
false,
false,
false.
false的分布列为:
false
0
1
2
3
false
false
false
false
false
false.
19.(1)false;(2)分布列见解析;期望为false.
【详解】
解:(1)甲赢两场,分下面三种情况
①第一场甲胜,第二场无甲,第三场甲胜
概率为:false ;
②第一场甲输,二三场均胜
概率为:false;
③第一场甲胜,第二场输,第三场胜
概率为:false ;
由互斥事件的概率加法公式可知:比赛进行了false场且甲晋级的概率为:false.
(2)依题意false的所有可能取值为false,false,false
由(1)知false,
当比赛进行了false场后结束,甲获胜的场数为false时,
分两种情况:
3场比赛中甲参加了1场,输了,概率为:false
3场比赛中甲参加了2场,都输了,概率为:false
3场比赛甲都参加且都输掉是不可能的,否则两场比赛打不到3场.
所以false,
故false,
故false的分布列为
false
false
false
false
false
false
false
false
则false.
20.(1)false;(2)答案见解析.
【详解】
解析(1)因为是各自随机“亮”出正反面,所以甲?乙“亮”出正面的概率均可认为是false,
设乙在此游戏中的收益为随机变量false,则false的可能取值为false,1,3,
所以可得乙的收益的分布列为
false
-2
1
3
false
false
false
false
false.
(2)假设甲以false的概率“亮”出正面,乙以false的概率“亮”出正面,
甲收益的随机变量为false,乙收益的随机变量为false,此时甲的收益分布列为
false
2
-1
-3
false
false
false
false
所以甲的收益期望为falsefalse.
同理可得乙的收益分布列为
false
-2
1
3
false
false
false
false
所以乙的收益期望为falsefalse.
根据甲的收益期望,可知乙的最优策略是“亮”出正面的概率为false,
否则若false,有false,甲的收益期望false,
甲可以选择都“亮”出反面的策略,即false,达到预期收益最大,此时false.
若false,则甲选择都“亮”出正面的策略,即false,达到预期收益最大,false.
同理,可知甲的最优策略是“亮”出正面的概率为false,
所以最终两人的决策为保持“亮”出正面的概率都为false.
而当false时,false,false,
所以此时游戏结果对两人都是最有利,但是规则不公平.
