3.1.2分 段 函 数 (练习题)- 2021-2022学年高一上学期数学人教A版(2019)必修第一册(Word版含解析)
文档属性
| 名称 | 3.1.2分 段 函 数 (练习题)- 2021-2022学年高一上学期数学人教A版(2019)必修第一册(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 339.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-08 19:55:51 | ||
图片预览


文档简介
分 段 函 数
一、选择题(每小题5分,共20分)
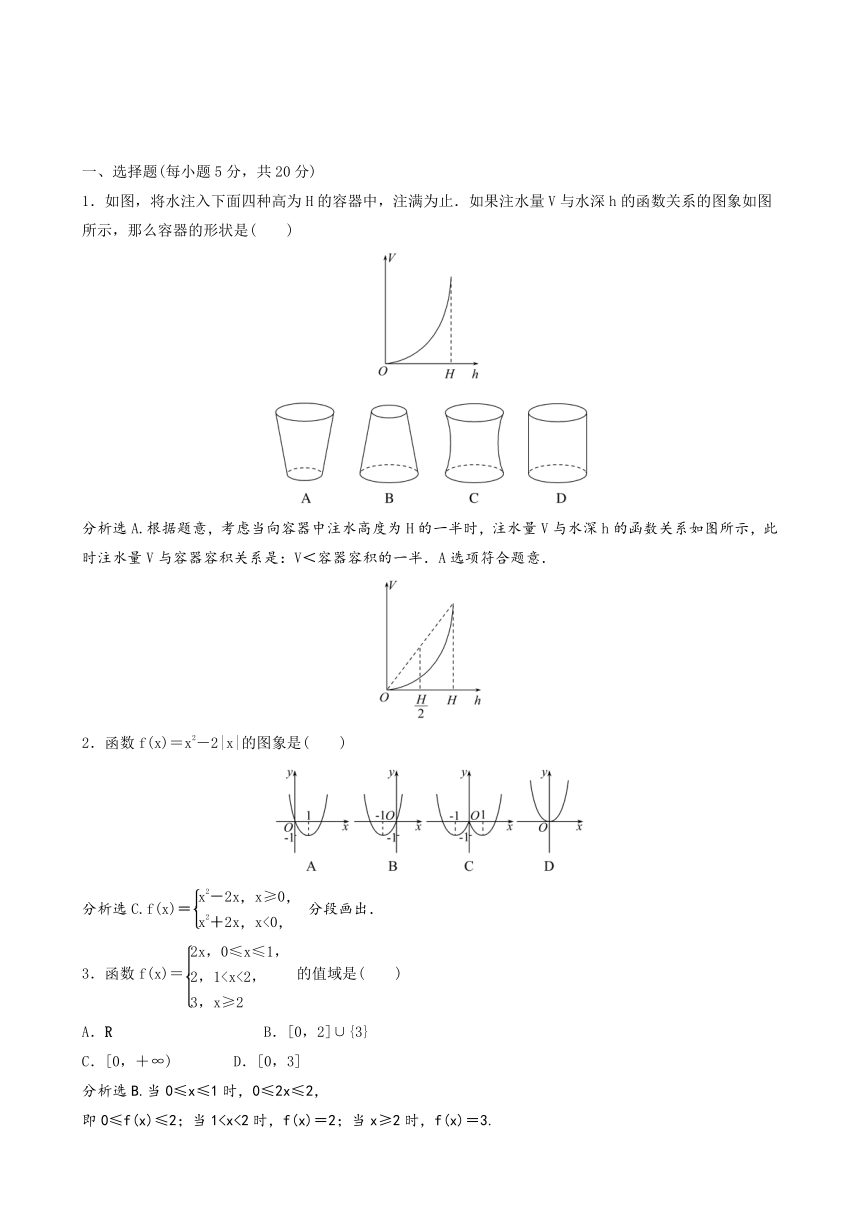
1.如图,将水注入下面四种高为H的容器中,注满为止.如果注水量V与水深h的函数关系的图象如图所示,那么容器的形状是( )
2.函数f(x)=x2-2|x|的图象是( )
3.函数f(x)=的值域是( )
A.R B.[0,2]∪{3}
C.[0,+∞) D.[0,3]
4.某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水量不超过10 m3的,按每立方米m元收费;用水量超过10 m3的,超过部分按每立方米2m元收费.某职工某月缴水费16m元,则该职工这个月实际用水量为( )
A.13 m3 B.14 m3
C.18 m3 D.26 m3
二、填空题(每小题5分,共10分)
5.已知函数f(x)=则f=________,若f(f(0))=a,则实数a=________.
6.设函数f(x)=若f(m)>m,则实数m的取值范围是________.
三、解答题
7.(10分)如图,某灌溉渠的横断面是等腰梯形,底宽为2 m,渠深为1.8 m,斜坡的倾斜角是45°.(临界状态不考虑)
(1)试将横断面中水的面积A(m2)表示成水深h(m)的函数;
(2)确定函数的定义域和值域.
能力过关
一、选择题(每小题5分,共10分)
1.设f(x)=若f(a)=f(a+2),则f=( )
A.2 B.4 C.6 D.8
2.(多选题)已知函数y=若f(a)=10,则a的可取值是( )
A.3 B.-3 C.-5 D.5
二、填空题(每小题5分,共10分)
3.新定义运算=若f(x)=,则=________.
4.加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”.在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系p=at2+bt+c(a,b,c是常数),如图记录了三次试验的数据.根据该函数模型和试验数据,可以得到最佳加工时间为________分钟.
三、解答题
5.(10分)已知函数f(x)=
(1)画出函数f(x)的简图(不必列表);
(2)求f[f(3)]的值;
(3)当-4≤x<3时,求f(x)取值的集合.
一、选择题(每小题5分,共20分)
1.如图,将水注入下面四种高为H的容器中,注满为止.如果注水量V与水深h的函数关系的图象如图所示,那么容器的形状是( )
分析选A.根据题意,考虑当向容器中注水高度为H的一半时,注水量V与水深h的函数关系如图所示,此时注水量V与容器容积关系是:V<容器容积的一半.A选项符合题意.
2.函数f(x)=x2-2|x|的图象是( )
分析选C.f(x)=分段画出.
3.函数f(x)=的值域是( )
A.R B.[0,2]∪{3}
C.[0,+∞) D.[0,3]
分析选B.当0≤x≤1时,0≤2x≤2,
即0≤f(x)≤2;当1综上可知f(x)的值域为[0,2]∪{3}.
4.某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水量不超过10 m3的,按每立方米m元收费;用水量超过10 m3的,超过部分按每立方米2m元收费.某职工某月缴水费16m元,则该职工这个月实际用水量为( )
A.13 m3 B.14 m3
C.18 m3 D.26 m3
分析选A.该单位职工每月应缴水费y与实际用水量x满足的关系式为
y=
由y=16m,可知x>10.
令2mx-10m=16m,解得x=13.
二、填空题(每小题5分,共10分)
5.已知函数f(x)=则f=________,若f(f(0))=a,则实数a=________.
分析依题意知f=1-a;f(0)=3×0+2=2,
则f(f(0))=f(2)=22-2a=a,求得a=.
答案:1-a
6.设函数f(x)=若f(m)>m,则实数m的取值范围是________.
分析由题意,得或
解得m<-1.
答案:(-∞,-1)
三、解答题
7.(10分)如图,某灌溉渠的横断面是等腰梯形,底宽为2 m,渠深为1.8 m,斜坡的倾斜角是45°.(临界状态不考虑)
(1)试将横断面中水的面积A(m2)表示成水深h(m)的函数;
(2)确定函数的定义域和值域.
分析 (1)由已知,横断面为等腰梯形,下底为2 m,上底为(2+2h)m,高为h m,
所以横断面中水的面积A==h2+2h(m2).
(2)定义域为{h|0由函数A=h2+2h=(h+1)2-1的图象(图略)可知,在区间(0,1.8)上函数值随自变量的增大而增大,所以0能力过关
一、选择题(每小题5分,共10分)
1.设f(x)=若f(a)=f(a+2),则f=( )
A.2 B.4 C.6 D.8
分析选B.若0<a<2,则a+2>2,
由f(a)=f(a+2),得=2(a+2)-4,
解得a=或a=0(舍去),
所以f=f(4)=2×4-4=4.
若a≥2,由f(a)=f(a+2),得2a-4=2(a+2)-4,无解.
综上,f=4.
2.(多选题)已知函数y=若f(a)=10,则a的可取值是( )
A.3 B.-3 C.-5 D.5
分析选BD.若a≤0,则f(a)=a2+1=10,
所以a=-3(a=3舍去).若a>0,则f(a)=2a=10,所以a=5.
综上可得,a=5或a=-3.
二、填空题(每小题5分,共10分)
3.新定义运算=若f(x)=,则=________.
分析由题意知f(x)=
且x≠0,所以f(x)=
所以=,
所以=f=.
答案:
4.加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”.在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系p=at2+bt+c(a,b,c是常数),如图记录了三次试验的数据.根据该函数模型和试验数据,可以得到最佳加工时间为________分钟.
分析由题意知,函数关系p=at2+bt+c(a,b,c是常数)经过点(3,0.7),(4,0.8),(5,0.5),
所以
解得a=-0.2,b=1.5,c=-2,
所以p=-0.2t2+1.5t-2=-0.2(t-3.75)2+0.812 5,
所以得到最佳加工时间为3.75分钟.
答案:3.75
三、解答题
5.(10分)已知函数f(x)=
(1)画出函数f(x)的简图(不必列表);
(2)求f[f(3)]的值;
(3)当-4≤x<3时,求f(x)取值的集合.
分析(1)由分段函数可知,函数f(x)的简图为:
(2)因为f(3)=4-32=4-9=-5,
所以f[f(3)]=f(-5)=1-2(-5)=1+10=11;
(3)当-4≤x<0时,1<f(x)≤9,
当x=0时f(0)=2,当0<x<3时,-5<f(x)<4,
综上:-5<f(x)≤9.
一、选择题(每小题5分,共20分)
1.如图,将水注入下面四种高为H的容器中,注满为止.如果注水量V与水深h的函数关系的图象如图所示,那么容器的形状是( )
2.函数f(x)=x2-2|x|的图象是( )
3.函数f(x)=的值域是( )
A.R B.[0,2]∪{3}
C.[0,+∞) D.[0,3]
4.某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水量不超过10 m3的,按每立方米m元收费;用水量超过10 m3的,超过部分按每立方米2m元收费.某职工某月缴水费16m元,则该职工这个月实际用水量为( )
A.13 m3 B.14 m3
C.18 m3 D.26 m3
二、填空题(每小题5分,共10分)
5.已知函数f(x)=则f=________,若f(f(0))=a,则实数a=________.
6.设函数f(x)=若f(m)>m,则实数m的取值范围是________.
三、解答题
7.(10分)如图,某灌溉渠的横断面是等腰梯形,底宽为2 m,渠深为1.8 m,斜坡的倾斜角是45°.(临界状态不考虑)
(1)试将横断面中水的面积A(m2)表示成水深h(m)的函数;
(2)确定函数的定义域和值域.
能力过关
一、选择题(每小题5分,共10分)
1.设f(x)=若f(a)=f(a+2),则f=( )
A.2 B.4 C.6 D.8
2.(多选题)已知函数y=若f(a)=10,则a的可取值是( )
A.3 B.-3 C.-5 D.5
二、填空题(每小题5分,共10分)
3.新定义运算=若f(x)=,则=________.
4.加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”.在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系p=at2+bt+c(a,b,c是常数),如图记录了三次试验的数据.根据该函数模型和试验数据,可以得到最佳加工时间为________分钟.
三、解答题
5.(10分)已知函数f(x)=
(1)画出函数f(x)的简图(不必列表);
(2)求f[f(3)]的值;
(3)当-4≤x<3时,求f(x)取值的集合.
一、选择题(每小题5分,共20分)
1.如图,将水注入下面四种高为H的容器中,注满为止.如果注水量V与水深h的函数关系的图象如图所示,那么容器的形状是( )
分析选A.根据题意,考虑当向容器中注水高度为H的一半时,注水量V与水深h的函数关系如图所示,此时注水量V与容器容积关系是:V<容器容积的一半.A选项符合题意.
2.函数f(x)=x2-2|x|的图象是( )
分析选C.f(x)=分段画出.
3.函数f(x)=的值域是( )
A.R B.[0,2]∪{3}
C.[0,+∞) D.[0,3]
分析选B.当0≤x≤1时,0≤2x≤2,
即0≤f(x)≤2;当1
4.某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水量不超过10 m3的,按每立方米m元收费;用水量超过10 m3的,超过部分按每立方米2m元收费.某职工某月缴水费16m元,则该职工这个月实际用水量为( )
A.13 m3 B.14 m3
C.18 m3 D.26 m3
分析选A.该单位职工每月应缴水费y与实际用水量x满足的关系式为
y=
由y=16m,可知x>10.
令2mx-10m=16m,解得x=13.
二、填空题(每小题5分,共10分)
5.已知函数f(x)=则f=________,若f(f(0))=a,则实数a=________.
分析依题意知f=1-a;f(0)=3×0+2=2,
则f(f(0))=f(2)=22-2a=a,求得a=.
答案:1-a
6.设函数f(x)=若f(m)>m,则实数m的取值范围是________.
分析由题意,得或
解得m<-1.
答案:(-∞,-1)
三、解答题
7.(10分)如图,某灌溉渠的横断面是等腰梯形,底宽为2 m,渠深为1.8 m,斜坡的倾斜角是45°.(临界状态不考虑)
(1)试将横断面中水的面积A(m2)表示成水深h(m)的函数;
(2)确定函数的定义域和值域.
分析 (1)由已知,横断面为等腰梯形,下底为2 m,上底为(2+2h)m,高为h m,
所以横断面中水的面积A==h2+2h(m2).
(2)定义域为{h|0
一、选择题(每小题5分,共10分)
1.设f(x)=若f(a)=f(a+2),则f=( )
A.2 B.4 C.6 D.8
分析选B.若0<a<2,则a+2>2,
由f(a)=f(a+2),得=2(a+2)-4,
解得a=或a=0(舍去),
所以f=f(4)=2×4-4=4.
若a≥2,由f(a)=f(a+2),得2a-4=2(a+2)-4,无解.
综上,f=4.
2.(多选题)已知函数y=若f(a)=10,则a的可取值是( )
A.3 B.-3 C.-5 D.5
分析选BD.若a≤0,则f(a)=a2+1=10,
所以a=-3(a=3舍去).若a>0,则f(a)=2a=10,所以a=5.
综上可得,a=5或a=-3.
二、填空题(每小题5分,共10分)
3.新定义运算=若f(x)=,则=________.
分析由题意知f(x)=
且x≠0,所以f(x)=
所以=,
所以=f=.
答案:
4.加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”.在特定条件下,可食用率p与加工时间t(单位:分钟)满足函数关系p=at2+bt+c(a,b,c是常数),如图记录了三次试验的数据.根据该函数模型和试验数据,可以得到最佳加工时间为________分钟.
分析由题意知,函数关系p=at2+bt+c(a,b,c是常数)经过点(3,0.7),(4,0.8),(5,0.5),
所以
解得a=-0.2,b=1.5,c=-2,
所以p=-0.2t2+1.5t-2=-0.2(t-3.75)2+0.812 5,
所以得到最佳加工时间为3.75分钟.
答案:3.75
三、解答题
5.(10分)已知函数f(x)=
(1)画出函数f(x)的简图(不必列表);
(2)求f[f(3)]的值;
(3)当-4≤x<3时,求f(x)取值的集合.
分析(1)由分段函数可知,函数f(x)的简图为:
(2)因为f(3)=4-32=4-9=-5,
所以f[f(3)]=f(-5)=1-2(-5)=1+10=11;
(3)当-4≤x<0时,1<f(x)≤9,
当x=0时f(0)=2,当0<x<3时,-5<f(x)<4,
综上:-5<f(x)≤9.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
