七年级数学 直线和圆的位置关系(1)切线及切线性质定理
文档属性
| 名称 | 七年级数学 直线和圆的位置关系(1)切线及切线性质定理 |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-30 12:06:41 | ||
图片预览





文档简介
(共20张PPT)
商水实验中学 初三数学组
一:知识回顾
1.点与圆有那几种位置关系?
2.怎样判断点与圆的位置关系?
点在圆上;点在圆外;点在圆内
用圆心到点的距离d与圆的半径r相比较:
(1)d>r 点在圆外
(2)d=r 点在圆上
(3)d<r 点在圆内
教学目标:
1.经历探索直线与圆位置关系的过程。
2.理解直线与圆有三种位置关系。
3.利用数量关系会判定直线与圆的位置关系。
自学指导:
自学内容:课本93-94页.
自学时间:5分钟。
自学要求:紧张,高效,活跃。
直线与圆位置关系
直线与圆的位置关系
思考1:
观察三幅太阳升起的照片,地平线与太阳的位置关系是怎样的
●O
●O
●O
驶向胜利的彼岸
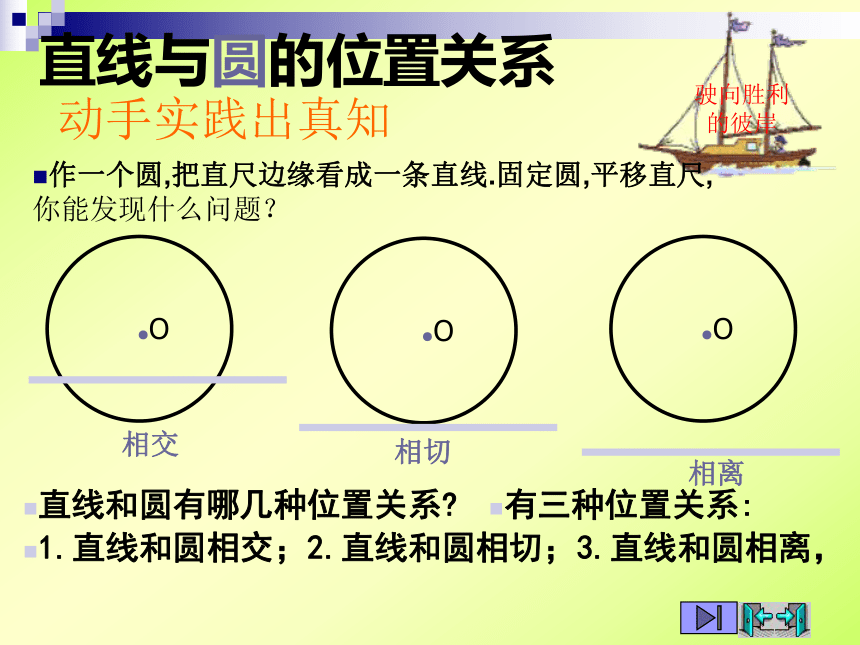
直线与圆的位置关系
直线和圆有哪几种位置关系
●O
●O
有三种位置关系:
相交
1.直线和圆相交;2.直线和圆相切;3.直线和圆相离,
●O
相切
相离
动手实践出真知
作一个圆,把直尺边缘看成一条直线.固定圆,平移直尺,
你能发现什么问题?
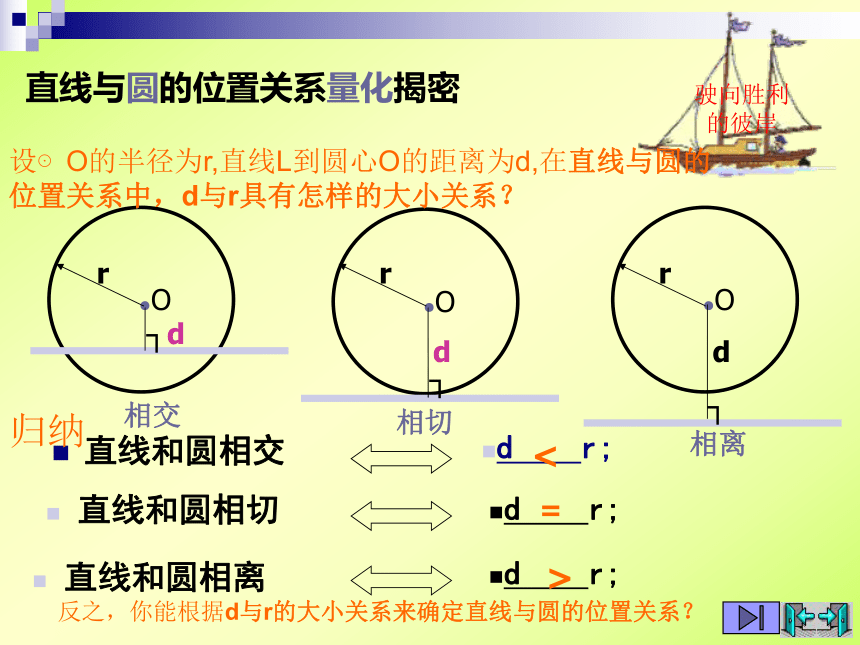
直线和圆相交
驶向胜利的彼岸
d r;
d r;
直线和圆相切
直线和圆相离
d r;
直线与圆的位置关系量化揭密
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
<
=
>
设⊙O的半径为r,直线L到圆心O的距离为d,在直线与圆的
位置关系中,d与r具有怎样的大小关系?
反之,你能根据d与r的大小关系来确定直线与圆的位置关系?
归纳
自学检测练1
1. ⊙O的半径为6cm,如果直线与圆心O的距离分别是(1)5cm;
(2)6cm;
(3)10cm.
试判断直线和⊙O的位置关系.
直线和圆相交
直线和圆相切
直线和圆相离
提示:直线L和圆O相离 d>r
直线L和圆O相切 d=r
直线L和圆O相交 d在Rt△ABC中,∠C=90,AC=3cm,BC=4cm, 以C为圆心,r为半径的圆与直线AB有怎样的位置关系?为什么?
(1) r=2cm (2) r=2.4cm (3) r=3cm
∟
A
B
C
D
A
B
C
D
A
B
C
D
(1)相离 (2)相切 (3)相交
自学检测练2
直线与圆的位置关系
公共点个数
公共点名称
直线名称
数量关系
d r
割线 切线 无
交点 切点 无
2
1
0
直线和圆的三种位置关系
相离
相切
相交
要点归纳1
2
1
0
相交
2
1
0
相交
要点归纳2
要判断直线和圆的位置关系首先由圆心向直线作垂线,再计算垂线段的长度,最后用垂线段的长度与圆的半径相比较.
如何判断直线和圆的位置关系?
如图,已知∠AOB= 30°,M为OB上一点,且OM=5cm,若以M为圆心,r为半径作圆,那么:
1)当直线OA与⊙M相离时, r的取值范围是
2)当直线OA与⊙M相切时, r的取值范围是
3)当直线OA与⊙M相交时, r的取值范围是
4)当直线OA与⊙M有公共点时, r的取值范围是
O
0cm < r < 2.5cm
r = 2.5cm
r>2.5cm
30°
A
B
强化训练
r≥2.5cm
M
C
同学们,交流以下,通过本节的学习,你都学到了什么?
1.直线与圆的位置关系:
(1).直线和圆相交;(2).直线和圆相切;(3).直线和圆相离
2.直线与圆的位置关系与圆心到直线的距离d与圆的半径r之间的数量关系.
选择题:
1、直线L上的一点到圆心O的距离等于⊙O的半径,则直线L与⊙O的位置关系是( )
(A)相离(B)相切(C)相交(D)相切或相交
2、已知等腰梯形ABCD上底AD长为3,下底BC长为11,一腰AB长为5,以A为圆心,AD为半径的圆与底BC的位置关系是( )
(A)相离(B)相交(C)相切(D)以上均错
D
C
课堂作业
课本101页1,2,3题
结束寄语
下课了!
商水实验中学 初三数学组
一:知识回顾
1.点与圆有那几种位置关系?
2.怎样判断点与圆的位置关系?
点在圆上;点在圆外;点在圆内
用圆心到点的距离d与圆的半径r相比较:
(1)d>r 点在圆外
(2)d=r 点在圆上
(3)d<r 点在圆内
教学目标:
1.经历探索直线与圆位置关系的过程。
2.理解直线与圆有三种位置关系。
3.利用数量关系会判定直线与圆的位置关系。
自学指导:
自学内容:课本93-94页.
自学时间:5分钟。
自学要求:紧张,高效,活跃。
直线与圆位置关系
直线与圆的位置关系
思考1:
观察三幅太阳升起的照片,地平线与太阳的位置关系是怎样的
●O
●O
●O
驶向胜利的彼岸
直线与圆的位置关系
直线和圆有哪几种位置关系
●O
●O
有三种位置关系:
相交
1.直线和圆相交;2.直线和圆相切;3.直线和圆相离,
●O
相切
相离
动手实践出真知
作一个圆,把直尺边缘看成一条直线.固定圆,平移直尺,
你能发现什么问题?
直线和圆相交
驶向胜利的彼岸
d r;
d r;
直线和圆相切
直线和圆相离
d r;
直线与圆的位置关系量化揭密
●O
●O
相交
●O
相切
相离
r
r
r
┐d
d
┐
d
┐
<
=
>
设⊙O的半径为r,直线L到圆心O的距离为d,在直线与圆的
位置关系中,d与r具有怎样的大小关系?
反之,你能根据d与r的大小关系来确定直线与圆的位置关系?
归纳
自学检测练1
1. ⊙O的半径为6cm,如果直线与圆心O的距离分别是(1)5cm;
(2)6cm;
(3)10cm.
试判断直线和⊙O的位置关系.
直线和圆相交
直线和圆相切
直线和圆相离
提示:直线L和圆O相离 d>r
直线L和圆O相切 d=r
直线L和圆O相交 d
(1) r=2cm (2) r=2.4cm (3) r=3cm
∟
A
B
C
D
A
B
C
D
A
B
C
D
(1)相离 (2)相切 (3)相交
自学检测练2
直线与圆的位置关系
公共点个数
公共点名称
直线名称
数量关系
d
割线 切线 无
交点 切点 无
2
1
0
直线和圆的三种位置关系
相离
相切
相交
要点归纳1
2
1
0
相交
2
1
0
相交
要点归纳2
要判断直线和圆的位置关系首先由圆心向直线作垂线,再计算垂线段的长度,最后用垂线段的长度与圆的半径相比较.
如何判断直线和圆的位置关系?
如图,已知∠AOB= 30°,M为OB上一点,且OM=5cm,若以M为圆心,r为半径作圆,那么:
1)当直线OA与⊙M相离时, r的取值范围是
2)当直线OA与⊙M相切时, r的取值范围是
3)当直线OA与⊙M相交时, r的取值范围是
4)当直线OA与⊙M有公共点时, r的取值范围是
O
0cm < r < 2.5cm
r = 2.5cm
r>2.5cm
30°
A
B
强化训练
r≥2.5cm
M
C
同学们,交流以下,通过本节的学习,你都学到了什么?
1.直线与圆的位置关系:
(1).直线和圆相交;(2).直线和圆相切;(3).直线和圆相离
2.直线与圆的位置关系与圆心到直线的距离d与圆的半径r之间的数量关系.
选择题:
1、直线L上的一点到圆心O的距离等于⊙O的半径,则直线L与⊙O的位置关系是( )
(A)相离(B)相切(C)相交(D)相切或相交
2、已知等腰梯形ABCD上底AD长为3,下底BC长为11,一腰AB长为5,以A为圆心,AD为半径的圆与底BC的位置关系是( )
(A)相离(B)相交(C)相切(D)以上均错
D
C
课堂作业
课本101页1,2,3题
结束寄语
下课了!
