6.2 排列与组合 学案-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(Word含答案)
文档属性
| 名称 | 6.2 排列与组合 学案-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(Word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 133.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-09 00:00:00 | ||
图片预览

文档简介
第六章计数原理
第六章计数原理
6.2 排列与组合
6.2 排列与组合
知识解读
知识解读
知识点一排列
排列的定义:一般地,从n 个不同元素中取出m(m≤n)个元素,并按照一定的顺序_________一列,叫做从n个不同元素中取出m个元素的一个排列
排列数的定义:
从n 个不同元素中取出m(m≤n)个元素的_________不同排列的个数,叫做从n 个不同元素中取出m个元素的排列数,用符号_________表示
排列数公式的两种形式
(1)A=n(n-1)(n-2)…(n-m+1),其中m,n∈N*,并且_________
(2)A=.
全排列:把n个不同的元素全部取出的一个排列,叫做n个元素的一个全排列,全排列数为A=n!(叫做n的阶乘).规定:_________
排列相同的条件
两个排列相同的充要条件:
(1)两个排列的_________完全相同.
(2)元素的排列_________也相同.
知识点二组合
组合定义
一般地,从n个不同元素中取出m(m≤n)个元素_________,叫做从n个不同元素中取出m个元素的一个组合.
组合数
从n个不同元素中取出m(m≤n)个元素的_________,叫做从n个不同元素中取出m个元素的组合数,用符号_________表示.
组合数公式
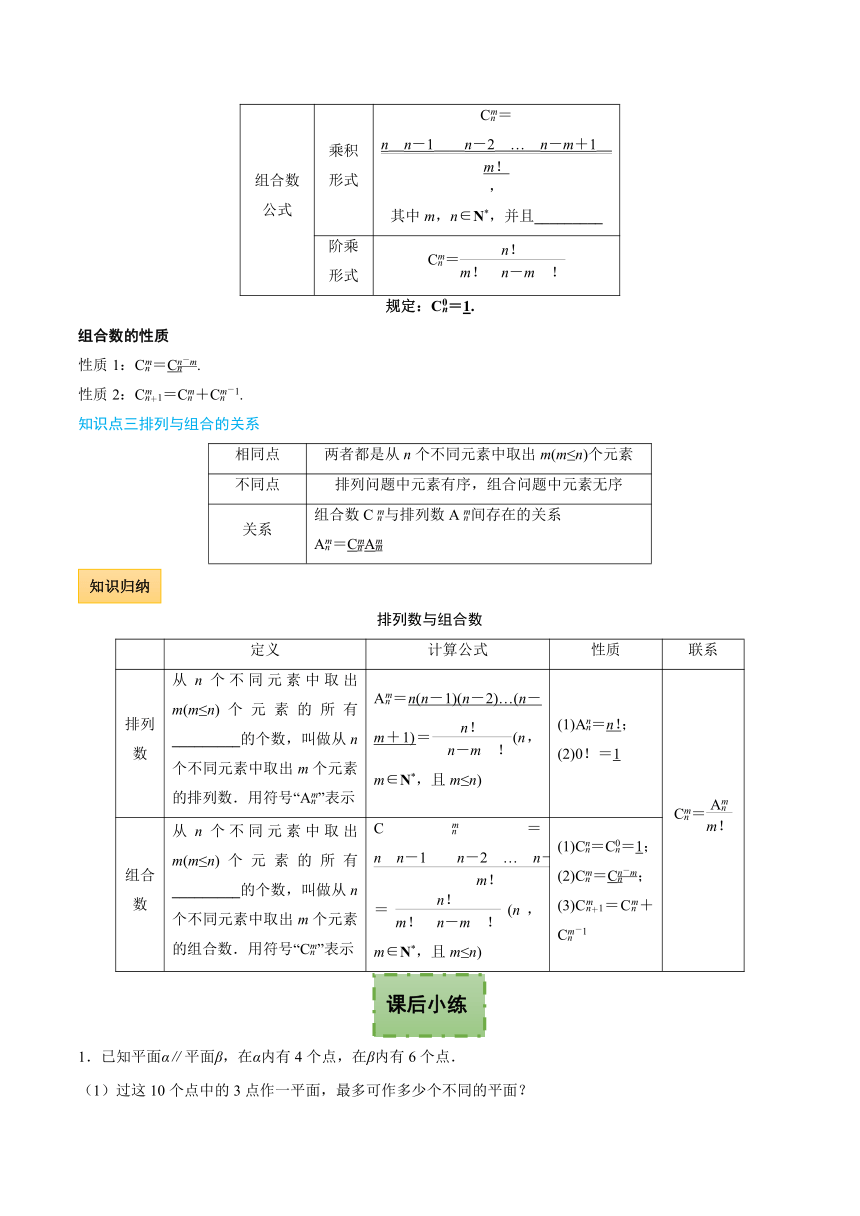
组合数
公式
乘积
形式
C=,
其中m,n∈N*,并且_________
阶乘
形式
C=
规定:C=1.
组合数的性质
性质1:C=C.
性质2:C=C+C.
知识点三排列与组合的关系
相同点
两者都是从n个不同元素中取出m(m≤n)个元素
不同点
排列问题中元素有序,组合问题中元素无序
关系
组合数C与排列数A间存在的关系
A=CA
知识归纳
知识归纳
排列数与组合数
定义
计算公式
性质
联系
排列数
从n个不同元素中取出m(m≤n)个元素的所有_________的个数,叫做从n个不同元素中取出m个元素的排列数.用符号“A”表示
A=n(n-1)(n-2)…(n-m+1)=(n,m∈N*,且m≤n)
(1)A=n!;
(2)0!=1
C=
组合数
从n个不同元素中取出m(m≤n)个元素的所有_________的个数,叫做从n个不同元素中取出m个元素的组合数.用符号“C”表示
C==(n,m∈N*,且m≤n)
(1)C=C=1;
(2)C=C;
(3)C=C+C
课后小练
课后小练
1.已知平面α∥平面β,在α内有4个点,在β内有6个点.
(1)过这10个点中的3点作一平面,最多可作多少个不同的平面?
(2)以这些点为顶点,最多可作多少个三棱锥?
(3)(2)中的三棱锥最多可以有多少个不同体积?
2.判断下列问题是否是排列问题.
(1)同宿舍4人,每两人互通一封信,他们一共写了多少封信?
(2)同宿舍4人,每两人通一次电话,他们一共通了几次电话?
3.有false个男生和false个女生,从中选取false人担任false门不同学科的科代表,求分别符合下列条件的选法数:
(1)有女生但人数必须少于男生;
(2)某女生一定要担任语文科代表;
(3)某男生必须包括在内,但不担任数学科代表;
(4)某女生一定要担任语文科代表,某男生必须担任科代表,但不担任数学科代表.
4.(1)从false本不同的书中选false本送给false名同学,每人各false本,共有多少种不同的送法?
(2)从false种不同的书中买false本送给false名同学,每人各false本,共有多少种不同的送法?
5.在甲、乙等6个单位参加的一次“唱读讲传”演出活动中,每个单位的节目集中安排在一起,若采用抽签的方式随机确定各单位的演出顺序(序号为1,2,…,6),求甲、乙两单位的演出序号至少有一个为奇数的概率.
6.从false,false,false,false,false这七个数字中任取三个不同的数字,分别作为函数false的系数false,false,false,求:
false可组成多少个不同的二次函数?
false其中对称轴是false轴的抛物线有多少条?
7.从1到7的7个数字中取两个偶数和三个奇数组成没有重复数字的五位数.试问:
(1)五位数中,两个偶数排在一起的有几个?
(2)两个偶数不相邻且三个奇数也不相邻的五位数有几个?(所有结果均用数值表示)
参考答案
1.(1)98(个);(2)194(个);(3)114个.
【详解】
解:(1)所作出的平面有三类.
①α内1点,β内2点确定的平面,最多有false个.
②α内2点,β内1点确定的平面,最多有false个.
③α,β本身,有2个.
故所作的平面最多有false+false+2=98(个).
(2)所作的三棱锥有三类.
①α内1点,β内3点确定的三棱锥,最多有false个.
②α内2点,β内2点确定的三棱锥,最多有false个.
③α内3点,β内1点确定的三棱锥,最多有false个.
故最多可作出的三棱锥有false+false+false=194(个).
(3)当等底面积、等高时,三棱锥的体积相等.
所以体积不相同的三棱锥最多有false+false+false=114(个).
故最多有114个体积不同的三棱锥.
2.(1)是;(2)不是.
【详解】
(1)是一个排列问题,相当于从4个人中任取两个人,并且按顺序排好.
(2)不是排列问题,“通电话”不讲顺序,甲与乙通了电话,也就是乙与甲通了电话.
3.(1)540;(2)840;(3)3360;(4)360.
【详解】
(1)先取后排,有false种,后排有false种,共有false种;
(2)除去该女生后先取后排:false种;
(3)先取后排,但先安排该男生:false种;
(4)先从除去该男生该女生的false人中选false人有false种,再安排该男生有false种,其余false人全排有false种,共false种.
4.(1)60;(2)125.
【详解】
(1)从false本不同的书中选出false本分别送给false名同学,
对应于从false个不同元素中任取false个元素的一个排列,
因此不同送法的种数是false.
(2)由于有false种不同的书,送给每个同学的false本书都有false种不同的选购方法,
因此送给false名同学每人各false本书的不同方法种数是false.
5.false
【详解】
甲、乙两单位从偶数中选出2个位置再排序,其余的全排列共有:falsefalse,
所以甲、乙两单位的演出序号都在偶数的概率为:false,
所以甲、乙两单位的演出序号至少有一个为奇数的概率为false.
6.false180个;false30条.
【详解】
解:false由二次函数的定义,false,则false有false种取法;在剩下的false个数字中取两个作为false和false,有false种.所以共有二次函数false(个);
false要求对称轴是false轴,则false,在余下的6个数字中取两个作为false和false,有false条.
7.(1)576;(2)144
【详解】
解:可知从1到7的7个数字中,有3个偶数,4个奇数,
(1)五位数中,偶数排在一起的有:false个,
(2)两个偶数不相邻且三个奇数也不相邻的五位数有:false个.
第六章计数原理
6.2 排列与组合
6.2 排列与组合
知识解读
知识解读
知识点一排列
排列的定义:一般地,从n 个不同元素中取出m(m≤n)个元素,并按照一定的顺序_________一列,叫做从n个不同元素中取出m个元素的一个排列
排列数的定义:
从n 个不同元素中取出m(m≤n)个元素的_________不同排列的个数,叫做从n 个不同元素中取出m个元素的排列数,用符号_________表示
排列数公式的两种形式
(1)A=n(n-1)(n-2)…(n-m+1),其中m,n∈N*,并且_________
(2)A=.
全排列:把n个不同的元素全部取出的一个排列,叫做n个元素的一个全排列,全排列数为A=n!(叫做n的阶乘).规定:_________
排列相同的条件
两个排列相同的充要条件:
(1)两个排列的_________完全相同.
(2)元素的排列_________也相同.
知识点二组合
组合定义
一般地,从n个不同元素中取出m(m≤n)个元素_________,叫做从n个不同元素中取出m个元素的一个组合.
组合数
从n个不同元素中取出m(m≤n)个元素的_________,叫做从n个不同元素中取出m个元素的组合数,用符号_________表示.
组合数公式
组合数
公式
乘积
形式
C=,
其中m,n∈N*,并且_________
阶乘
形式
C=
规定:C=1.
组合数的性质
性质1:C=C.
性质2:C=C+C.
知识点三排列与组合的关系
相同点
两者都是从n个不同元素中取出m(m≤n)个元素
不同点
排列问题中元素有序,组合问题中元素无序
关系
组合数C与排列数A间存在的关系
A=CA
知识归纳
知识归纳
排列数与组合数
定义
计算公式
性质
联系
排列数
从n个不同元素中取出m(m≤n)个元素的所有_________的个数,叫做从n个不同元素中取出m个元素的排列数.用符号“A”表示
A=n(n-1)(n-2)…(n-m+1)=(n,m∈N*,且m≤n)
(1)A=n!;
(2)0!=1
C=
组合数
从n个不同元素中取出m(m≤n)个元素的所有_________的个数,叫做从n个不同元素中取出m个元素的组合数.用符号“C”表示
C==(n,m∈N*,且m≤n)
(1)C=C=1;
(2)C=C;
(3)C=C+C
课后小练
课后小练
1.已知平面α∥平面β,在α内有4个点,在β内有6个点.
(1)过这10个点中的3点作一平面,最多可作多少个不同的平面?
(2)以这些点为顶点,最多可作多少个三棱锥?
(3)(2)中的三棱锥最多可以有多少个不同体积?
2.判断下列问题是否是排列问题.
(1)同宿舍4人,每两人互通一封信,他们一共写了多少封信?
(2)同宿舍4人,每两人通一次电话,他们一共通了几次电话?
3.有false个男生和false个女生,从中选取false人担任false门不同学科的科代表,求分别符合下列条件的选法数:
(1)有女生但人数必须少于男生;
(2)某女生一定要担任语文科代表;
(3)某男生必须包括在内,但不担任数学科代表;
(4)某女生一定要担任语文科代表,某男生必须担任科代表,但不担任数学科代表.
4.(1)从false本不同的书中选false本送给false名同学,每人各false本,共有多少种不同的送法?
(2)从false种不同的书中买false本送给false名同学,每人各false本,共有多少种不同的送法?
5.在甲、乙等6个单位参加的一次“唱读讲传”演出活动中,每个单位的节目集中安排在一起,若采用抽签的方式随机确定各单位的演出顺序(序号为1,2,…,6),求甲、乙两单位的演出序号至少有一个为奇数的概率.
6.从false,false,false,false,false这七个数字中任取三个不同的数字,分别作为函数false的系数false,false,false,求:
false可组成多少个不同的二次函数?
false其中对称轴是false轴的抛物线有多少条?
7.从1到7的7个数字中取两个偶数和三个奇数组成没有重复数字的五位数.试问:
(1)五位数中,两个偶数排在一起的有几个?
(2)两个偶数不相邻且三个奇数也不相邻的五位数有几个?(所有结果均用数值表示)
参考答案
1.(1)98(个);(2)194(个);(3)114个.
【详解】
解:(1)所作出的平面有三类.
①α内1点,β内2点确定的平面,最多有false个.
②α内2点,β内1点确定的平面,最多有false个.
③α,β本身,有2个.
故所作的平面最多有false+false+2=98(个).
(2)所作的三棱锥有三类.
①α内1点,β内3点确定的三棱锥,最多有false个.
②α内2点,β内2点确定的三棱锥,最多有false个.
③α内3点,β内1点确定的三棱锥,最多有false个.
故最多可作出的三棱锥有false+false+false=194(个).
(3)当等底面积、等高时,三棱锥的体积相等.
所以体积不相同的三棱锥最多有false+false+false=114(个).
故最多有114个体积不同的三棱锥.
2.(1)是;(2)不是.
【详解】
(1)是一个排列问题,相当于从4个人中任取两个人,并且按顺序排好.
(2)不是排列问题,“通电话”不讲顺序,甲与乙通了电话,也就是乙与甲通了电话.
3.(1)540;(2)840;(3)3360;(4)360.
【详解】
(1)先取后排,有false种,后排有false种,共有false种;
(2)除去该女生后先取后排:false种;
(3)先取后排,但先安排该男生:false种;
(4)先从除去该男生该女生的false人中选false人有false种,再安排该男生有false种,其余false人全排有false种,共false种.
4.(1)60;(2)125.
【详解】
(1)从false本不同的书中选出false本分别送给false名同学,
对应于从false个不同元素中任取false个元素的一个排列,
因此不同送法的种数是false.
(2)由于有false种不同的书,送给每个同学的false本书都有false种不同的选购方法,
因此送给false名同学每人各false本书的不同方法种数是false.
5.false
【详解】
甲、乙两单位从偶数中选出2个位置再排序,其余的全排列共有:falsefalse,
所以甲、乙两单位的演出序号都在偶数的概率为:false,
所以甲、乙两单位的演出序号至少有一个为奇数的概率为false.
6.false180个;false30条.
【详解】
解:false由二次函数的定义,false,则false有false种取法;在剩下的false个数字中取两个作为false和false,有false种.所以共有二次函数false(个);
false要求对称轴是false轴,则false,在余下的6个数字中取两个作为false和false,有false条.
7.(1)576;(2)144
【详解】
解:可知从1到7的7个数字中,有3个偶数,4个奇数,
(1)五位数中,偶数排在一起的有:false个,
(2)两个偶数不相邻且三个奇数也不相邻的五位数有:false个.
