6.1 分类加法计数原理与分步乘法计数原理 学案-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(Word含答案)
文档属性
| 名称 | 6.1 分类加法计数原理与分步乘法计数原理 学案-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(Word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 213.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-09 12:58:34 | ||
图片预览


文档简介
第六章计数原理
第六章计数原理
6.1分类加法计数原理与分步乘法计数原理
6.1分类加法计数原理与分步乘法计数原理
知识解读
知识解读
考点一分类加法计数原理
完成一件事有两类方案
在第1类方案中有m种不同的方法
在第2类方案中有n种不同的方法,那么完成这件事共有N=_________种不同的方法.
考点二 使用分类加法计数原理计数的两个条件
(1)根据问题的特点确定一个适合它的_________,在这个标准下进行分类.
(2)完成这件事的任何一种方法_________属于某一类,分别属于不同类的两种方法是不同的方法,满足这些条件,才可以用__________________
考点三 分步乘法计数原理
完成一件事需要两个步骤
做第1步有m种不同的方法
做第2步有n种不同的方法,那么完成这件事共有N=_________种不同的方法.
考点四 分类加法计数原理与分步乘法计数原理的联系与区别
联系:是涉及做一件事的_________的种数问题.
区别:分类加法计数原理针对的是“_________”问题,其中各种方法相互独立,用其中任何一种方法都可以做完这件事;分步乘法计数原理针对的是“_________”问题,各个步骤中的方
法_________,只有各个步骤都完成才算做完这件事.
考点四两个计数原理的应用
用两个计数原理解决计数问题时,最重要的是在开始计算之前要仔细分析两点:
(1)分类要做到“_________”,分类后再分别对每一类进行计数,最后用分类加法计数原理求和,得到总数.
(2)分步要做到“_________”,即完成了所有步骤,恰好完成任务.分类后再计算每一步的方法数,最后根据分步乘法计数原理,把完成每一步的方法数相乘,得到总数.
知识归纳
知识归纳
基本形式
一般形式
区别
分类加法计数原理
完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法,那么完成这件事共有N=m+n种不同的方法
完成一件事有n类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法,…,在第n类方案中有mn种不同的方法,那么完成这件事共有N=m1+m2+…+mn种不同的方法
分类加法计数原理与分步乘法计数原理,都涉及完成一件事情的不同方法种数.它们的区别在于:分类加法计数原理与分类有关,各种方法相互独立,用其中的任何一种方法都可以完成这件事;分步乘法计数原理与分步有关,各个步骤相互依存,只有各个步骤都完成了,这件事才算完成
分步乘法计数原理
完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,那么完成这件事共有N=m×n种不同的方法
完成一件事需要n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,…,做第n步有mn种不同的方法,那么完成这件事共有N=m1×m2×…×mn种不同的方法
课后小练
课后小练
1.用0,1,…,9这十个数字可以组成多少个
(1)三位整数?
(2)无重复数字的三位整数?
(3)小于500的无重复数字的三位整数?
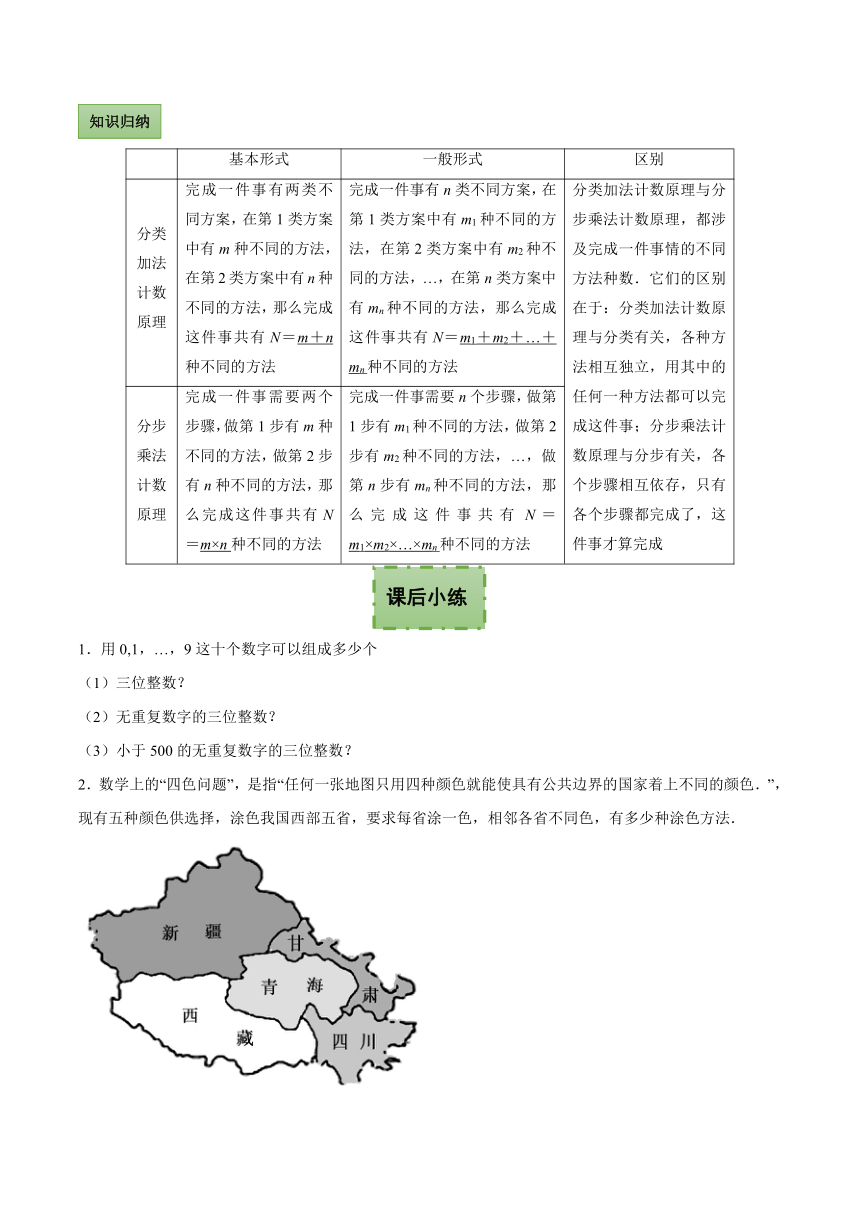
2.数学上的“四色问题”,是指“任何一张地图只用四种颜色就能使具有公共边界的国家着上不同的颜色.”,现有五种颜色供选择,涂色我国西部五省,要求每省涂一色,相邻各省不同色,有多少种涂色方法.
3.用5种不同的颜色给图中的四个区域涂色,每个区域涂一种颜色,若要求相邻(有公共边)的区域不同色,则共有多少种不同的涂色方法?
1
2
3
4
4.男运动员false名,女运动员false名,其中男女队长各false人,选派false人外出比赛,在下列情形中各有多少种选派方法.
(1)任选false人
(2)男运动员false名,女运动员false名
(3)至少有false名女运动员
(4)队长至少有一人参加
(5)既要有队长,又要有女运动员
5.一次数学考试有4道填空题,共20分,每道题完全答对得5分,否则得0分.在试卷命题时,设计第一道题使考生都能完全答对,后三道题能得出正确答案的概率分别为false、false、false,且每题答对与否相互独立.
(1)当false时,求考生填空题得满分的概率;
(2)若考生填空题得10分与得15分的概率相等,求false的值.
6.如图,将四棱锥S-ABCD的每一个顶点涂上一种颜色,并使同一条棱的两端点异色,如果只有5种颜色可供使用,那么有多少种不同的涂色方法?
7.某城市地铁公司为鼓励人们绿色出行,决定按照乘客经过地铁站的数量实施分段优惠政策,不超过9站的地铁票价如表:
乘坐站数
0<x≤3
3<x≤6
6<x≤9
票价(元)
2
3
4
现有小华、小李两位乘客同时从起点乘坐同一辆地铁,已知他们乘坐地铁都不超过9站,且他们各自在每个站下地铁的可能性是相同的.
(1)若小华、小李两人共付费5元,则小华、小李下地铁的方案共有多少种?
(2)若小华、小李两人共付费6元,求小华比小李先下地铁的概率.
参考答案
1.(1)900个;(2)648个;(3)288个.
【详解】
解:由于0不可在最高位,因此应对它进行单独考虑.
(1)百位的数字有9种选择,十位和个位的数字都各有10种选择,由分步乘法计数原理知,符合题意的三位数共有9×10×10=900(个).
(2)由于数字不可重复,可知百位的数字有9种选择,十位的数字也有9种选择,但个位数字仅有8种选择,由分步乘法计数原理知,符合题意的三位数共有9×9×8=648(个).
(3)百位只有4种选择,十位可有9种选择,个位数字有8种选择,由分步乘法计数原理知,符合题意的三位数共有4×9×8=288(个).
2.420种方法
【详解】
对于新疆有5种涂色的方法,
对于青海有4种涂色方法,
对于西藏有3种涂色方法,
对于四川:若与新疆颜色相同,则有1种涂色方法,此时甘肃有3种涂色方法;
若四川与新疆颜色不相同,则四川只有2种涂色方法,此时甘肃有2种涂色方法;
根据分步、分类计数原理,则共有5×4×3×(2×2+1×3)=420种方法.
3.260
【详解】
解:第一类,1号区域与4号区域同色,此时可分三步来完成,
第一步,涂1号区域和4号区域,有5种涂法;
第二步,涂2号区域,只要不与1号区域和4号区域同色即可,因此有4种涂法;
第三步,涂3号区域,只要不与1号区域和4号区域同色即可,因此也有4种涂法.
由分步乘法计数原理知,有5×4×4=80种涂法.
第二类,1号区域与4号区域不同色,此时可分四步来完成,
第一步,涂1号区域,有5种涂法;
第二步,涂4号区域,只要不与1号区域同色即可,因此有4种涂法;
第三步,涂2号区域,只要不与1号区域和4号区域同色即可,因此有3种涂法;
第四步,涂3号区域,只要不与1号区域和4号区域同色即可,因此也有3种涂法.
由分步乘法计数原理知,有5×4×3×3=180种涂法.
依据分类加法计数原理知,不同涂色的方法种数为80+180=260.
4.(1)252(2)120(3)246(4)196(5)191
【详解】
(1)false 男运动员false名,女运动员false名,共false名
false 任选false人的选法为:false
false 任选false人,共有false种选法.
(2)false 选派男运动员false名,女运动员false名.
false 首先选false名男运动员,有false种选法,再选false名女运动员,有false种选法
false 根据分步计数乘法原理
false 选派男运动员false名,女运动员false名,共有false种选法.
(3)false 至少false名女运动员包括以下几种情况:false女false男,false女false男,false女false男,false女false男.
false 由分类加法计数原理可得有:false.
false 至少有false名女运动员有false种选法.
(4)false 只有男队长的选法为false选法,只有女队长的选法为false选法
又false 男、女队长都入选的选法为false选法.
false 共有false种选法.
false 队长至少有一人参加有:false种选法.
(5)false 当有女队长,其他人选法任意,共有false种选法,
false 不选女队长时,必选男队长,共有false种选法,
选男队长且不含女运动员有false种选法.
false不选女队长时共有false种选法.
false 既有队长又有女运动员共有:false种选法.
5.(1)false;(2)false
【详解】
设考生填空题得满分、15分、10分为事件A、B、C
(1)false
(2)false=false
false =false
因为false , 所以false=false得false
6.420
【解析】
先给点S涂色,有5种不同的方法,再给点A涂色,有4种不同的方法,接着给点B涂色,有3种不同的方法,当点C与点A同色时,给点D涂色有3种不同的方法;当点C与点A不同色时,给点C涂色有2种不同的方法,给点D涂色也有2种不同的方法,依据分类加法计数原理和分步乘法计数原理可知不同的涂色方法共有5×4×3×(3+2×2)=420(种).
7.(1)18,(2)false
【详解】
(1)小华、小李两人共付费5元,所以小华、小李一人付费2元一人付费3元,付费2元的乘坐站数有1,2,3三种选择,付费3元的乘坐站数有4,5,6三种选择,所以小华、小李下地铁的方案共有false种;
(2)小华、小李两人共付费6元,所以小华、小李一人付费2元一人付费4元或两人都付费3元,付费4元的乘坐站数也有7,8,9三种选择,因此小华、小李下地铁的方案共有false种;其中小华比小李先下地铁的方案共有false种;因此小华比小李先下地铁的概率为false
第六章计数原理
6.1分类加法计数原理与分步乘法计数原理
6.1分类加法计数原理与分步乘法计数原理
知识解读
知识解读
考点一分类加法计数原理
完成一件事有两类方案
在第1类方案中有m种不同的方法
在第2类方案中有n种不同的方法,那么完成这件事共有N=_________种不同的方法.
考点二 使用分类加法计数原理计数的两个条件
(1)根据问题的特点确定一个适合它的_________,在这个标准下进行分类.
(2)完成这件事的任何一种方法_________属于某一类,分别属于不同类的两种方法是不同的方法,满足这些条件,才可以用__________________
考点三 分步乘法计数原理
完成一件事需要两个步骤
做第1步有m种不同的方法
做第2步有n种不同的方法,那么完成这件事共有N=_________种不同的方法.
考点四 分类加法计数原理与分步乘法计数原理的联系与区别
联系:是涉及做一件事的_________的种数问题.
区别:分类加法计数原理针对的是“_________”问题,其中各种方法相互独立,用其中任何一种方法都可以做完这件事;分步乘法计数原理针对的是“_________”问题,各个步骤中的方
法_________,只有各个步骤都完成才算做完这件事.
考点四两个计数原理的应用
用两个计数原理解决计数问题时,最重要的是在开始计算之前要仔细分析两点:
(1)分类要做到“_________”,分类后再分别对每一类进行计数,最后用分类加法计数原理求和,得到总数.
(2)分步要做到“_________”,即完成了所有步骤,恰好完成任务.分类后再计算每一步的方法数,最后根据分步乘法计数原理,把完成每一步的方法数相乘,得到总数.
知识归纳
知识归纳
基本形式
一般形式
区别
分类加法计数原理
完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法,那么完成这件事共有N=m+n种不同的方法
完成一件事有n类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法,…,在第n类方案中有mn种不同的方法,那么完成这件事共有N=m1+m2+…+mn种不同的方法
分类加法计数原理与分步乘法计数原理,都涉及完成一件事情的不同方法种数.它们的区别在于:分类加法计数原理与分类有关,各种方法相互独立,用其中的任何一种方法都可以完成这件事;分步乘法计数原理与分步有关,各个步骤相互依存,只有各个步骤都完成了,这件事才算完成
分步乘法计数原理
完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,那么完成这件事共有N=m×n种不同的方法
完成一件事需要n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,…,做第n步有mn种不同的方法,那么完成这件事共有N=m1×m2×…×mn种不同的方法
课后小练
课后小练
1.用0,1,…,9这十个数字可以组成多少个
(1)三位整数?
(2)无重复数字的三位整数?
(3)小于500的无重复数字的三位整数?
2.数学上的“四色问题”,是指“任何一张地图只用四种颜色就能使具有公共边界的国家着上不同的颜色.”,现有五种颜色供选择,涂色我国西部五省,要求每省涂一色,相邻各省不同色,有多少种涂色方法.
3.用5种不同的颜色给图中的四个区域涂色,每个区域涂一种颜色,若要求相邻(有公共边)的区域不同色,则共有多少种不同的涂色方法?
1
2
3
4
4.男运动员false名,女运动员false名,其中男女队长各false人,选派false人外出比赛,在下列情形中各有多少种选派方法.
(1)任选false人
(2)男运动员false名,女运动员false名
(3)至少有false名女运动员
(4)队长至少有一人参加
(5)既要有队长,又要有女运动员
5.一次数学考试有4道填空题,共20分,每道题完全答对得5分,否则得0分.在试卷命题时,设计第一道题使考生都能完全答对,后三道题能得出正确答案的概率分别为false、false、false,且每题答对与否相互独立.
(1)当false时,求考生填空题得满分的概率;
(2)若考生填空题得10分与得15分的概率相等,求false的值.
6.如图,将四棱锥S-ABCD的每一个顶点涂上一种颜色,并使同一条棱的两端点异色,如果只有5种颜色可供使用,那么有多少种不同的涂色方法?
7.某城市地铁公司为鼓励人们绿色出行,决定按照乘客经过地铁站的数量实施分段优惠政策,不超过9站的地铁票价如表:
乘坐站数
0<x≤3
3<x≤6
6<x≤9
票价(元)
2
3
4
现有小华、小李两位乘客同时从起点乘坐同一辆地铁,已知他们乘坐地铁都不超过9站,且他们各自在每个站下地铁的可能性是相同的.
(1)若小华、小李两人共付费5元,则小华、小李下地铁的方案共有多少种?
(2)若小华、小李两人共付费6元,求小华比小李先下地铁的概率.
参考答案
1.(1)900个;(2)648个;(3)288个.
【详解】
解:由于0不可在最高位,因此应对它进行单独考虑.
(1)百位的数字有9种选择,十位和个位的数字都各有10种选择,由分步乘法计数原理知,符合题意的三位数共有9×10×10=900(个).
(2)由于数字不可重复,可知百位的数字有9种选择,十位的数字也有9种选择,但个位数字仅有8种选择,由分步乘法计数原理知,符合题意的三位数共有9×9×8=648(个).
(3)百位只有4种选择,十位可有9种选择,个位数字有8种选择,由分步乘法计数原理知,符合题意的三位数共有4×9×8=288(个).
2.420种方法
【详解】
对于新疆有5种涂色的方法,
对于青海有4种涂色方法,
对于西藏有3种涂色方法,
对于四川:若与新疆颜色相同,则有1种涂色方法,此时甘肃有3种涂色方法;
若四川与新疆颜色不相同,则四川只有2种涂色方法,此时甘肃有2种涂色方法;
根据分步、分类计数原理,则共有5×4×3×(2×2+1×3)=420种方法.
3.260
【详解】
解:第一类,1号区域与4号区域同色,此时可分三步来完成,
第一步,涂1号区域和4号区域,有5种涂法;
第二步,涂2号区域,只要不与1号区域和4号区域同色即可,因此有4种涂法;
第三步,涂3号区域,只要不与1号区域和4号区域同色即可,因此也有4种涂法.
由分步乘法计数原理知,有5×4×4=80种涂法.
第二类,1号区域与4号区域不同色,此时可分四步来完成,
第一步,涂1号区域,有5种涂法;
第二步,涂4号区域,只要不与1号区域同色即可,因此有4种涂法;
第三步,涂2号区域,只要不与1号区域和4号区域同色即可,因此有3种涂法;
第四步,涂3号区域,只要不与1号区域和4号区域同色即可,因此也有3种涂法.
由分步乘法计数原理知,有5×4×3×3=180种涂法.
依据分类加法计数原理知,不同涂色的方法种数为80+180=260.
4.(1)252(2)120(3)246(4)196(5)191
【详解】
(1)false 男运动员false名,女运动员false名,共false名
false 任选false人的选法为:false
false 任选false人,共有false种选法.
(2)false 选派男运动员false名,女运动员false名.
false 首先选false名男运动员,有false种选法,再选false名女运动员,有false种选法
false 根据分步计数乘法原理
false 选派男运动员false名,女运动员false名,共有false种选法.
(3)false 至少false名女运动员包括以下几种情况:false女false男,false女false男,false女false男,false女false男.
false 由分类加法计数原理可得有:false.
false 至少有false名女运动员有false种选法.
(4)false 只有男队长的选法为false选法,只有女队长的选法为false选法
又false 男、女队长都入选的选法为false选法.
false 共有false种选法.
false 队长至少有一人参加有:false种选法.
(5)false 当有女队长,其他人选法任意,共有false种选法,
false 不选女队长时,必选男队长,共有false种选法,
选男队长且不含女运动员有false种选法.
false不选女队长时共有false种选法.
false 既有队长又有女运动员共有:false种选法.
5.(1)false;(2)false
【详解】
设考生填空题得满分、15分、10分为事件A、B、C
(1)false
(2)false=false
false =false
因为false , 所以false=false得false
6.420
【解析】
先给点S涂色,有5种不同的方法,再给点A涂色,有4种不同的方法,接着给点B涂色,有3种不同的方法,当点C与点A同色时,给点D涂色有3种不同的方法;当点C与点A不同色时,给点C涂色有2种不同的方法,给点D涂色也有2种不同的方法,依据分类加法计数原理和分步乘法计数原理可知不同的涂色方法共有5×4×3×(3+2×2)=420(种).
7.(1)18,(2)false
【详解】
(1)小华、小李两人共付费5元,所以小华、小李一人付费2元一人付费3元,付费2元的乘坐站数有1,2,3三种选择,付费3元的乘坐站数有4,5,6三种选择,所以小华、小李下地铁的方案共有false种;
(2)小华、小李两人共付费6元,所以小华、小李一人付费2元一人付费4元或两人都付费3元,付费4元的乘坐站数也有7,8,9三种选择,因此小华、小李下地铁的方案共有false种;其中小华比小李先下地铁的方案共有false种;因此小华比小李先下地铁的概率为false
