8.2 一元线性回归模型及其应用 学案-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(wordl含答案)
文档属性
| 名称 | 8.2 一元线性回归模型及其应用 学案-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(wordl含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 295.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-09 00:00:00 | ||
图片预览




文档简介
第八章 成对数据的统计分析
第八章 成对数据的统计分析
8.2一元线性回归模型及其应用
8.2一元线性回归模型及其应用
知识梳理
知识梳理
知识点一 一元线性回归模型
称为Y关于x的一元线性回归模型.其中Y称为________或________变量,x称为自变量或解释变量,a称为________参数,b称为________参数;e是Y与bx+a之间的随机误差,如e=0,那么Y与x之间的关系就可以用一元线性函数模型来描述.
知识点二最小二乘法
线性回归方程与最小二乘法
将=x+称为Y关于x的经验回归方程,也称________________,其图形称为经验回归________,这种求经验回归方程的方法叫最小二乘法,求得的,叫做b,a的最小二乘估计,其中=,=-.
知识点三残差与残差分析
残差
对于响应变量Y,通过观测得到的数据称为________,通过经验回归方程得到的称为________值,观测值减去预测值称为________.
残差分析
残差是随机误差的估计结果,残差的分析可以判断模型刻画数据效果和判断原始数据中是否存在可疑数据等,称为残差分析.
知识点四对模型刻画数据效果的分析
残差图法
残差图中,如残差比较________地集中在以横轴为对称轴的水平带状区域内,说明经验回归方程较好地刻画两个变量的关系.
残差平方和法
残差平方和(yi-i)2越小,模型的拟合效果越________.
课后小练
课后小练
1.十四五发展纲要提出要推进能源革命,建设清洁低碳、安全高效的能源体系,加快发展非化石能源,大力提升风电、光伏发展规模,有序发展海上风电.海上风电相比与陆上风电有着一定的优势,海上风电可装的风机更大,风资源利用率更高,近几年我国海上风电事业发展良好.下面是近五年我国海上风电发展情况表和对应的散点图.
2016-2020年中国海上风电新增装机容量及累计装机容量表(单位:万千瓦)
年份
2016
2017
2018
2019
2020
年份代号t
1
2
3
4
5
新增装机容量u
31
69
140
219
306
累计装机容量v
104
173
313
532
838
(1)为了分析中国海上风电装机容量的情况,建立了false和false两个线性回归模型,你认为用哪个线性回归模型更可靠?并说明理由.
(2)根据(1)的判断结果及表中数据,求出回归方程,并根据这个回归模型回答下列问题:
①2021年我国海上风电新增装机容量的预测值是多少?
②预计至少要到哪一年,我国海上风电累计装机容量超过2000万千瓦?
参考数据:
false
false
false
false
765
2995
1960
7707
参考公式:回归方程false中false.
2.false年开始,小李在县城租房开了一间服装店,每年只卖甲品牌和乙品牌的服装.小李所租服装店每年的租金如下表:
年份
false
false
false
false
年份代号false
false
false
false
false
租金false(千元)
false
false
false
false
根据以往的统计可知,每年卖甲品牌服装的收入为false万元,卖乙品牌服装的收入为false万元.
(I)求false关于false的线性回归方程;
(II)由(I)求得的回归方程预测此服装店false年的利润为多少.(年利润false年收入false年租金)
参考公式:在线性回归方程false中,false,false.
3.新疆拥有巨大的植棉气候优势,日照时间长,光线充足,生长周期长,昼夜温差大,常年供不应求,品质属于世界顶级,植保无人机、打包采棉机、残膜回收机、智能深翻犁、……,这些智能机器,受到越来越多新疆棉农的青睐,新疆棉花生产早已经实现高度机械化,即使在忙碌的采摘季节,也不需要大量的“采棉工”,下表是新疆长绒棉近年来产量表:
年份
2015
2016
2017
2018
2019
2020
年份代码x
1
2
3
4
5
6
年产量y(百万吨)
6.6
6.7
7
7.1
7.2
7.4
(1)根据表中数据,建立y关于x的线性回归方程false;
(2)根据线性回归方程预测2021年新疆长绒棉的年产量.
附:对于一组数据false,false,…,false,其回归直线方程false的斜率和截距的最小二乘估计分别为false,false.
(参考数据:false,计算结果保留到小数点后两位)
4.某蛋糕店制作的蛋糕尺寸有6,8,10,12,14,16(单位:英寸)六种,根据日常销售统计,将蛋糕尺寸)、平均月销量false (个)以及成本和单价的数据整理得到如下的表格.
蛋糕尺寸x(英寸)
6
8
10
12
14
16
平均月销量y(个)
9
12
15
15
13
8
成本(元)
20
40
60
80
100
120
单价(元)
50
90
140
180
200
220
(1)求该蛋糕店销售蛋糕的平均月利润(利润=销售收入一成本);
(2)根据题中数据,从false与false两个模型中选择更合适的,建立false关于false的回方程(系数精确到0.01).
参考公式:对于一组数据false,其回归直线方程false的针率和截距的最小二乘法分别是false,false
参考数据:false,false, false
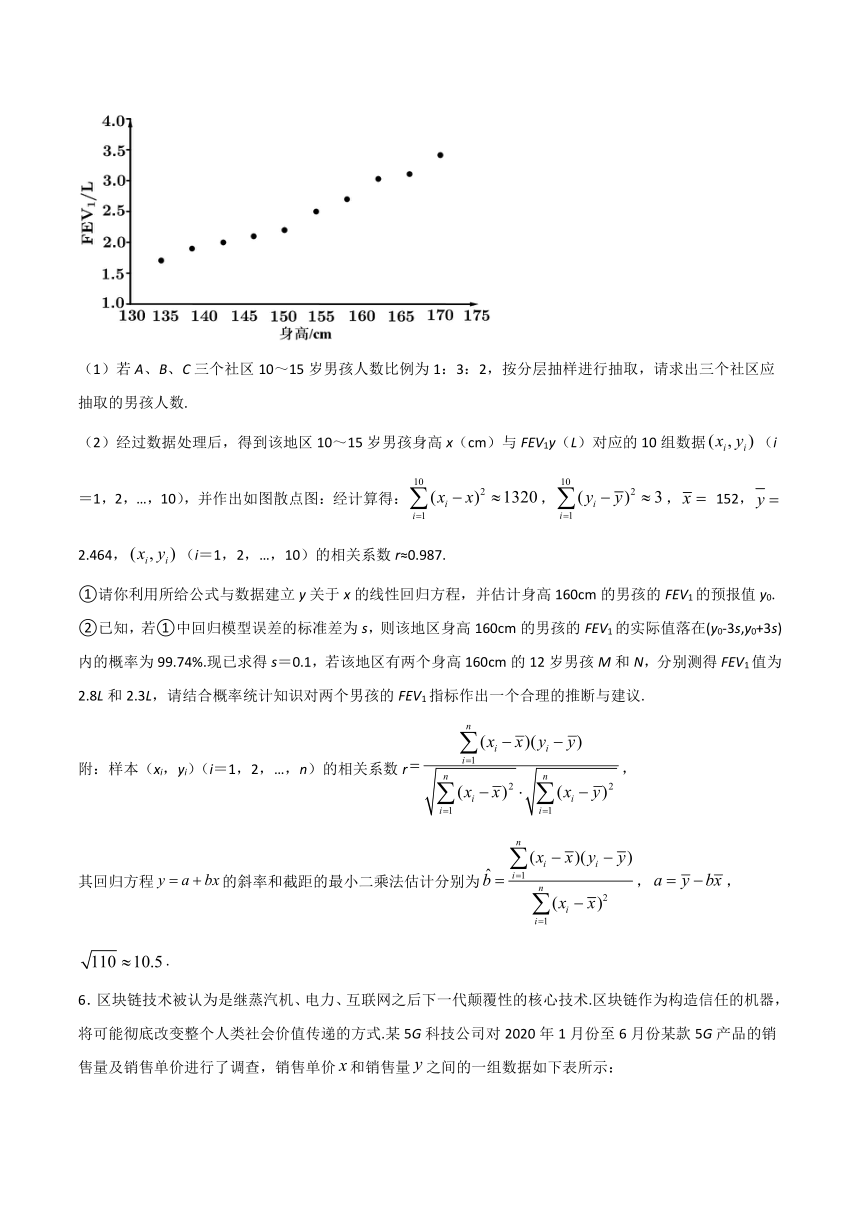
5.FEV1(一秒用力呼气容积)是肺功能的一个重要指标.为了研究某地区10~15岁男孩群体的FEV1与身高的关系,现从该地区A、B、C三个社区10~15岁男孩中随机抽取600名进行FEV1与身高数据的相关分析.
(1)若A、B、C三个社区10~15岁男孩人数比例为1:3:2,按分层抽样进行抽取,请求出三个社区应抽取的男孩人数.
(2)经过数据处理后,得到该地区10~15岁男孩身高x(cm)与FEV1y(L)对应的10组数据false(i=1,2,…,10),并作出如图散点图:经计算得:false,false,false 152,false 2.464,false(i=1,2,…,10)的相关系数r≈0.987.
①请你利用所给公式与数据建立y关于x的线性回归方程,并估计身高160cm的男孩的FEV1的预报值y0.
②已知,若①中回归模型误差的标准差为s,则该地区身高160cm的男孩的FEV1的实际值落在(y0-3s,y0+3s)内的概率为99.74%.现已求得s=0.1,若该地区有两个身高160cm的12岁男孩M和N,分别测得FEV1值为2.8L和2.3L,请结合概率统计知识对两个男孩的FEV1指标作出一个合理的推断与建议.
附:样本(xi,yi)(i=1,2,…,n)的相关系数rfalse,
其回归方程false的斜率和截距的最小二乘法估计分别为false,false,false.
6.区块链技术被认为是继蒸汽机、电力、互联网之后下一代颠覆性的核心技术.区块链作为构造信任的机器,将可能彻底改变整个人类社会价值传递的方式.某5G科技公司对2020年1月份至6月份某款5G产品的销售量及销售单价进行了调查,销售单价false和销售量false之间的一组数据如下表所示:
月份
1
2
3
4
5
6
月销售单价false(百元)
9
8.8
8.6
8.4
8.2
8
月销售量false(万件)
68
75
80
83
84
90
(1)由散点图可知变量false,false具有线性相关关系,根据1至6月份的数据,求出false关于false的回归直线方程;
(2)预计在今后的销售中,月销售量与月销售单价仍然服从(1)中的关系,若该种产品的成本是350元/件,那么该产品的月销售单价应定为多少元才能获得最大月利润?(注:利润=销售收入-成本)
参考公式和数据:false,false,其中false,false.
参考答案
1.(1)模型false更可靠,理由见解析;(2)①363;②2023年.
【详解】
(1)模型false更可靠.
原因:从散点图可以看出,左边的散点图上的点比右边散点图上的点更集中在一条直线的附近,说明变量u和t具有更强的线性相关关系.
(2)依题意得false,false,false,false,
所以false,则false,
所以false;
①当false时,2021年我国海上风电新增装机容量的预测值是false.
②当false时,2022年我国海上风电新增裝机容量的预测值是false.
当false时,2023年我国海上风电新增装机量的预测值是false
因为false,false;
所以预计至少要到2023年,我国海上风电累计装机量超过2000万千瓦.
2.(I)false;(II)14.45万元.
【详解】
命题意图 本题考查线性回归方程.
解析(I)根据表中数据,计算可得false,false,
false,
false
false,
false,
false关于false的线性回归方程为false
(II)将false代入回归方程得false(千元).
false预测第false年卖甲品牌服装的收入为false万元,卖乙品牌服装的收入为false万元,
false预测false年的利润为false(万元).
3.(1)false;(2)约为7.56百万吨.
【详解】
(1)由题意,根据表格中熟记,可得false,
false,
false,
所以false,
又由false,
所以false关于false的线性回归方程为false.
(2)由(1)可得,当年份为2021年时,年份代码为false,
此时false.
所以可预测2021年新疆长绒棉年产量约为7.56百万吨.
4.(1)6570元;(2)false.
【详解】
解:(1)根据题意,该蛋糕店销售蛋糕的平均月利润为
false元;
(2)由表中的数据可知false与false之间不是线性关系,所以选false,设false,则false,
false
false,false
所以false
因此y关于x的回归方程为false.
5.(1)A:100人,B:300人,C:200人;(2)①false,2.84,②答案见解析.
【详解】
(1)A社区抽取人数:false人;B社区抽取人数:false人;
C社区抽取人数:false人;
(2)①对比b与r的公式,得:
false,
∴false.
∴所求的线性回归方程为false,而当x=160时,预计y0=0.047×160-4.68=2.84;
②∵s=0.1,则y0 - 3s=2.84 - 3×0.1=2.54,y0+3s=2.84+3×0.1=3.14.
∴该地区身高160cm的男孩的FEV1的实际值落在区间(2.54,3.14)内的概率为99.74%,即该地区身高160cm的男孩的EFV1值不在这个区间内的概率极小,仅有0.26%,M的EFV1值落在这个区间内,我们推断他的EFV1是正常的,N的EFV1值低于该区间的下限,我们推断他的EFV1是不正常的,建议他去找一下不正常的原因.
6.(1)false;(2)800元.
【详解】
解:(1)根据表中数据,可得
false,false,
false.
因为false,
所以false,false,
所以false关于false的线性回归方程为false.
(2)设该产品的月销售单价为false百元,月利润为false百万元,
则由false,得false,
所以当false时,false(百万元),所以月销售单价应定为800元,才能获得最大月利润.
第八章 成对数据的统计分析
8.2一元线性回归模型及其应用
8.2一元线性回归模型及其应用
知识梳理
知识梳理
知识点一 一元线性回归模型
称为Y关于x的一元线性回归模型.其中Y称为________或________变量,x称为自变量或解释变量,a称为________参数,b称为________参数;e是Y与bx+a之间的随机误差,如e=0,那么Y与x之间的关系就可以用一元线性函数模型来描述.
知识点二最小二乘法
线性回归方程与最小二乘法
将=x+称为Y关于x的经验回归方程,也称________________,其图形称为经验回归________,这种求经验回归方程的方法叫最小二乘法,求得的,叫做b,a的最小二乘估计,其中=,=-.
知识点三残差与残差分析
残差
对于响应变量Y,通过观测得到的数据称为________,通过经验回归方程得到的称为________值,观测值减去预测值称为________.
残差分析
残差是随机误差的估计结果,残差的分析可以判断模型刻画数据效果和判断原始数据中是否存在可疑数据等,称为残差分析.
知识点四对模型刻画数据效果的分析
残差图法
残差图中,如残差比较________地集中在以横轴为对称轴的水平带状区域内,说明经验回归方程较好地刻画两个变量的关系.
残差平方和法
残差平方和(yi-i)2越小,模型的拟合效果越________.
课后小练
课后小练
1.十四五发展纲要提出要推进能源革命,建设清洁低碳、安全高效的能源体系,加快发展非化石能源,大力提升风电、光伏发展规模,有序发展海上风电.海上风电相比与陆上风电有着一定的优势,海上风电可装的风机更大,风资源利用率更高,近几年我国海上风电事业发展良好.下面是近五年我国海上风电发展情况表和对应的散点图.
2016-2020年中国海上风电新增装机容量及累计装机容量表(单位:万千瓦)
年份
2016
2017
2018
2019
2020
年份代号t
1
2
3
4
5
新增装机容量u
31
69
140
219
306
累计装机容量v
104
173
313
532
838
(1)为了分析中国海上风电装机容量的情况,建立了false和false两个线性回归模型,你认为用哪个线性回归模型更可靠?并说明理由.
(2)根据(1)的判断结果及表中数据,求出回归方程,并根据这个回归模型回答下列问题:
①2021年我国海上风电新增装机容量的预测值是多少?
②预计至少要到哪一年,我国海上风电累计装机容量超过2000万千瓦?
参考数据:
false
false
false
false
765
2995
1960
7707
参考公式:回归方程false中false.
2.false年开始,小李在县城租房开了一间服装店,每年只卖甲品牌和乙品牌的服装.小李所租服装店每年的租金如下表:
年份
false
false
false
false
年份代号false
false
false
false
false
租金false(千元)
false
false
false
false
根据以往的统计可知,每年卖甲品牌服装的收入为false万元,卖乙品牌服装的收入为false万元.
(I)求false关于false的线性回归方程;
(II)由(I)求得的回归方程预测此服装店false年的利润为多少.(年利润false年收入false年租金)
参考公式:在线性回归方程false中,false,false.
3.新疆拥有巨大的植棉气候优势,日照时间长,光线充足,生长周期长,昼夜温差大,常年供不应求,品质属于世界顶级,植保无人机、打包采棉机、残膜回收机、智能深翻犁、……,这些智能机器,受到越来越多新疆棉农的青睐,新疆棉花生产早已经实现高度机械化,即使在忙碌的采摘季节,也不需要大量的“采棉工”,下表是新疆长绒棉近年来产量表:
年份
2015
2016
2017
2018
2019
2020
年份代码x
1
2
3
4
5
6
年产量y(百万吨)
6.6
6.7
7
7.1
7.2
7.4
(1)根据表中数据,建立y关于x的线性回归方程false;
(2)根据线性回归方程预测2021年新疆长绒棉的年产量.
附:对于一组数据false,false,…,false,其回归直线方程false的斜率和截距的最小二乘估计分别为false,false.
(参考数据:false,计算结果保留到小数点后两位)
4.某蛋糕店制作的蛋糕尺寸有6,8,10,12,14,16(单位:英寸)六种,根据日常销售统计,将蛋糕尺寸)、平均月销量false (个)以及成本和单价的数据整理得到如下的表格.
蛋糕尺寸x(英寸)
6
8
10
12
14
16
平均月销量y(个)
9
12
15
15
13
8
成本(元)
20
40
60
80
100
120
单价(元)
50
90
140
180
200
220
(1)求该蛋糕店销售蛋糕的平均月利润(利润=销售收入一成本);
(2)根据题中数据,从false与false两个模型中选择更合适的,建立false关于false的回方程(系数精确到0.01).
参考公式:对于一组数据false,其回归直线方程false的针率和截距的最小二乘法分别是false,false
参考数据:false,false, false
5.FEV1(一秒用力呼气容积)是肺功能的一个重要指标.为了研究某地区10~15岁男孩群体的FEV1与身高的关系,现从该地区A、B、C三个社区10~15岁男孩中随机抽取600名进行FEV1与身高数据的相关分析.
(1)若A、B、C三个社区10~15岁男孩人数比例为1:3:2,按分层抽样进行抽取,请求出三个社区应抽取的男孩人数.
(2)经过数据处理后,得到该地区10~15岁男孩身高x(cm)与FEV1y(L)对应的10组数据false(i=1,2,…,10),并作出如图散点图:经计算得:false,false,false 152,false 2.464,false(i=1,2,…,10)的相关系数r≈0.987.
①请你利用所给公式与数据建立y关于x的线性回归方程,并估计身高160cm的男孩的FEV1的预报值y0.
②已知,若①中回归模型误差的标准差为s,则该地区身高160cm的男孩的FEV1的实际值落在(y0-3s,y0+3s)内的概率为99.74%.现已求得s=0.1,若该地区有两个身高160cm的12岁男孩M和N,分别测得FEV1值为2.8L和2.3L,请结合概率统计知识对两个男孩的FEV1指标作出一个合理的推断与建议.
附:样本(xi,yi)(i=1,2,…,n)的相关系数rfalse,
其回归方程false的斜率和截距的最小二乘法估计分别为false,false,false.
6.区块链技术被认为是继蒸汽机、电力、互联网之后下一代颠覆性的核心技术.区块链作为构造信任的机器,将可能彻底改变整个人类社会价值传递的方式.某5G科技公司对2020年1月份至6月份某款5G产品的销售量及销售单价进行了调查,销售单价false和销售量false之间的一组数据如下表所示:
月份
1
2
3
4
5
6
月销售单价false(百元)
9
8.8
8.6
8.4
8.2
8
月销售量false(万件)
68
75
80
83
84
90
(1)由散点图可知变量false,false具有线性相关关系,根据1至6月份的数据,求出false关于false的回归直线方程;
(2)预计在今后的销售中,月销售量与月销售单价仍然服从(1)中的关系,若该种产品的成本是350元/件,那么该产品的月销售单价应定为多少元才能获得最大月利润?(注:利润=销售收入-成本)
参考公式和数据:false,false,其中false,false.
参考答案
1.(1)模型false更可靠,理由见解析;(2)①363;②2023年.
【详解】
(1)模型false更可靠.
原因:从散点图可以看出,左边的散点图上的点比右边散点图上的点更集中在一条直线的附近,说明变量u和t具有更强的线性相关关系.
(2)依题意得false,false,false,false,
所以false,则false,
所以false;
①当false时,2021年我国海上风电新增装机容量的预测值是false.
②当false时,2022年我国海上风电新增裝机容量的预测值是false.
当false时,2023年我国海上风电新增装机量的预测值是false
因为false,false;
所以预计至少要到2023年,我国海上风电累计装机量超过2000万千瓦.
2.(I)false;(II)14.45万元.
【详解】
命题意图 本题考查线性回归方程.
解析(I)根据表中数据,计算可得false,false,
false,
false
false,
false,
false关于false的线性回归方程为false
(II)将false代入回归方程得false(千元).
false预测第false年卖甲品牌服装的收入为false万元,卖乙品牌服装的收入为false万元,
false预测false年的利润为false(万元).
3.(1)false;(2)约为7.56百万吨.
【详解】
(1)由题意,根据表格中熟记,可得false,
false,
false,
所以false,
又由false,
所以false关于false的线性回归方程为false.
(2)由(1)可得,当年份为2021年时,年份代码为false,
此时false.
所以可预测2021年新疆长绒棉年产量约为7.56百万吨.
4.(1)6570元;(2)false.
【详解】
解:(1)根据题意,该蛋糕店销售蛋糕的平均月利润为
false元;
(2)由表中的数据可知false与false之间不是线性关系,所以选false,设false,则false,
false
false,false
所以false
因此y关于x的回归方程为false.
5.(1)A:100人,B:300人,C:200人;(2)①false,2.84,②答案见解析.
【详解】
(1)A社区抽取人数:false人;B社区抽取人数:false人;
C社区抽取人数:false人;
(2)①对比b与r的公式,得:
false,
∴false.
∴所求的线性回归方程为false,而当x=160时,预计y0=0.047×160-4.68=2.84;
②∵s=0.1,则y0 - 3s=2.84 - 3×0.1=2.54,y0+3s=2.84+3×0.1=3.14.
∴该地区身高160cm的男孩的FEV1的实际值落在区间(2.54,3.14)内的概率为99.74%,即该地区身高160cm的男孩的EFV1值不在这个区间内的概率极小,仅有0.26%,M的EFV1值落在这个区间内,我们推断他的EFV1是正常的,N的EFV1值低于该区间的下限,我们推断他的EFV1是不正常的,建议他去找一下不正常的原因.
6.(1)false;(2)800元.
【详解】
解:(1)根据表中数据,可得
false,false,
false.
因为false,
所以false,false,
所以false关于false的线性回归方程为false.
(2)设该产品的月销售单价为false百元,月利润为false百万元,
则由false,得false,
所以当false时,false(百万元),所以月销售单价应定为800元,才能获得最大月利润.
