8.1 成对数据的统计相关性 学案-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(wordl含答案)
文档属性
| 名称 | 8.1 成对数据的统计相关性 学案-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(wordl含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 384.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-09 00:00:00 | ||
图片预览



文档简介
第八章 成对数据的统计分析
第八章 成对数据的统计分析
8.1成对数据的统计相关性
8.1成对数据的统计相关性
知识梳理
知识梳理
知识点1. 变量的相关关系
相关关系:两个变量________关系,但又________确切到可由其中的一个去精确地决定另一个的程度,这种关系称为________关系.
相关关系的分类
按变量间的增减性分为________相关和________相关.
①正相关:当一个变量的值________时,另一个变量的相应值也________
②负相关:当一个变量的值________时,另一个变量的相应值也________
按变量间是否有线性特征分为线性相关和非线性相关(曲线相关).
①线性相关:如果两个变量的取值呈现________相关或________相关,而且散点落在一条直线附近,我们称这两个变量________相关;
②非线性相关或曲线相关:如果两个变量具有________性,但不是线性相关,我们称这两个变量非线性相关
知识点2.相关关系的刻画
散点图::将样本中的每一个序号下的________样本数据都用直角坐标系中的点表示出来,由这些点组成的统计图叫做________.
样本相关系数
(1)我们常用样本相关系数r来确切地反映成对样本数据(xi,yi)的相关程度,其中r=.
(2)样本相关系数r的取值范围为[-1,1].
①若________时,成对样本数据正相关;
②若________时,成对样本数据负相关;
③当|r|越接近1时,成对样本数据的线性相关程度________;
④当|r|越接近0时,成对样本数据的线性相关程度________.
课后小练
课后小练
1.某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量false与尺寸false之间近似满足关系式false(false、false为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间false内时为优等品.现随机抽取false件合格产品,测得数据如下:
尺寸false
38
48
58
68
78
88
质量false
16.8
18.8
20.7
22.4
24
25.5
质量与尺寸的比false
0.442
0.392
0.357
0.329
0.308
0.290
(1)现从抽取的false件合格产品中再任选false件,记false为取到优等品的件数,试求随机变量false的期望;
(2)根据测得数据作了初步处理,得相关统计量的值如表:
false
false
false
false
false
false
false
false
(i)根据所给统计量,求false关于false的回归方程;
(ii)已知优等品的收益false(单位:千元)与false、false的关系为false,则当优等品的尺寸false为何值时,收益false的预报值最大?
附:对于样本false,其回归直线false的斜率和截距的最小二乘估计公式分别为:false,false,false.
2.商务部会同海关总署?国家药监局于3月31日发布关于有序开展医疗物资出口的公告.如医疗物资出口中出现质量问题,将认真调查,发现一起,查处一起,切实维护“中国制造”的形象,更好地发挥医疗物资对支持全球疫情防控的重要作用.为了监控某种医疗物资的一条生产线的生产过程,检验员每隔30false从该生产线上随机抽取一个医疗物资,并测量其尺寸(单位:false).下面是检验员在一天内依次抽取的16个医疗物资的尺寸:
抽取次数
1
2
3
4
5
6
7
8
医疗物资尺寸
false
false
false
false
false
false
false
false
抽取次数
9
10
11
12
13
14
15
16
医疗物资尺寸
false
false
false
false
false
false
false
false
经计算得false,false,false,false,false,其中false为抽取的第false个医疗物资的尺寸,false
(1)求false的相关系数false,并回答是否可以认为这一天生产的医疗物资尺寸不随生产过程的进行而系统地变大或变小(若false,则可以认为医疗物资尺寸不随生产过程的进行而系统地变大或变小).
(2)一天内抽检医疗物资中,如果出现了尺寸在false之外的医疗物资,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.从这一天抽检的结果看,是否需对当天的生产过程进行检查?
附:样本false的相关系数false
3.某地一公司的市场研究人员为了解公司生产的某产品的使用情况,从两个方面进行了调查统计,一是产品的质量参数x,二是产品的使用时间t(单位:千小时),经统计分析,质量参数x服从正态分布false,使用时间t与质量参数x之间有如下关系:
质量参数x
0.65
0.70
0.75
0.80
0.85
0.90
0.95
使用时间t
2.60
2.81
3.05
3.10
3.25
3.35
3.54
(1)该地监管部门对该公司的该产品进行检查,要求质量参数在0.785以上的产品为合格产品.现抽取20件该产品进行校验,求合格产品的件数的数学期望;
(2)该公司研究人员根据最小二乘法求得线性回归方程为false,请用相关系数说明使用时间t与质量参数x之间的关系是否可用线性回归模型拟合.
附:参考数据:false.若false,则false
参考公式:相关系数false;
回归直线方程为false,其中false.
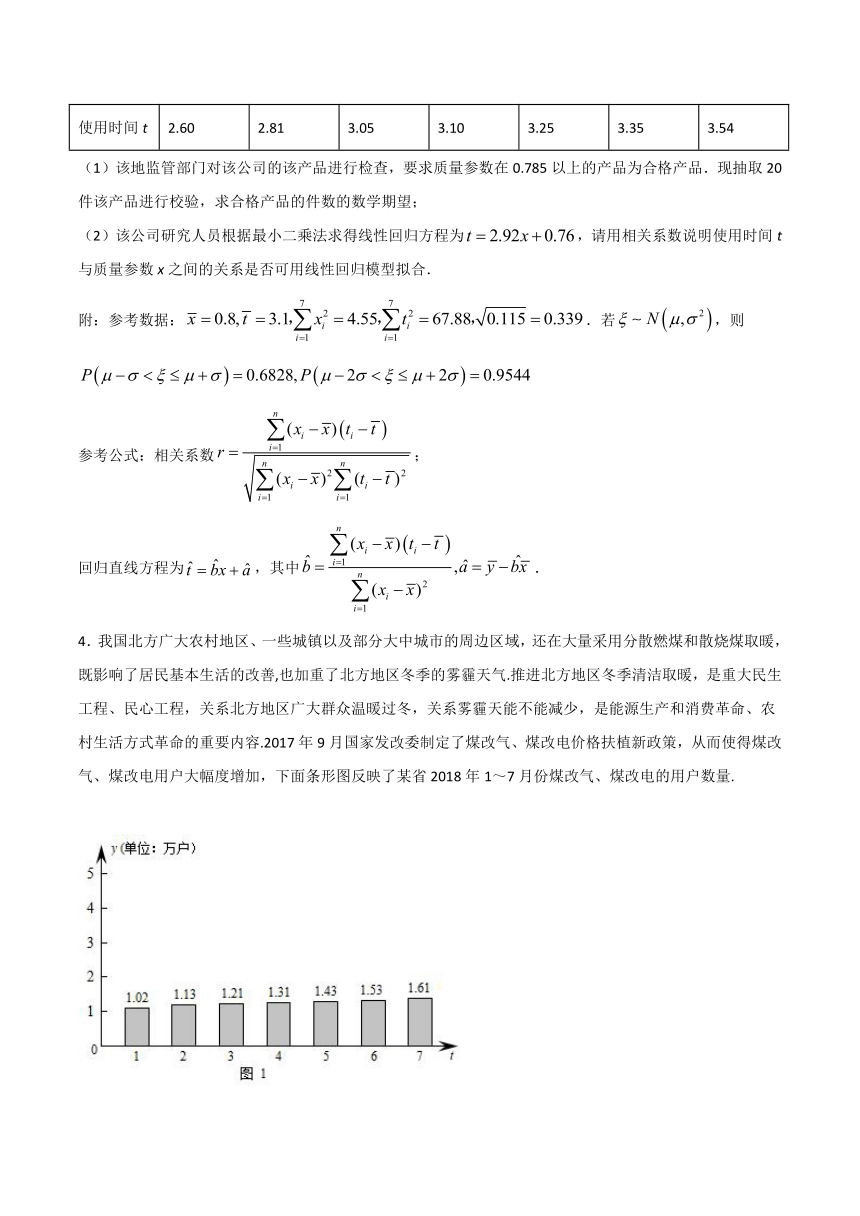
4.我国北方广大农村地区、一些城镇以及部分大中城市的周边区域,还在大量采用分散燃煤和散烧煤取暖,既影响了居民基本生活的改善,也加重了北方地区冬季的雾霾天气.推进北方地区冬季清洁取暖,是重大民生工程、民心工程,关系北方地区广大群众温暖过冬,关系雾霾天能不能减少,是能源生产和消费革命、农村生活方式革命的重要内容.2017年9月国家发改委制定了煤改气、煤改电价格扶植新政策,从而使得煤改气、煤改电用户大幅度增加,下面条形图反映了某省2018年1~7月份煤改气、煤改电的用户数量.
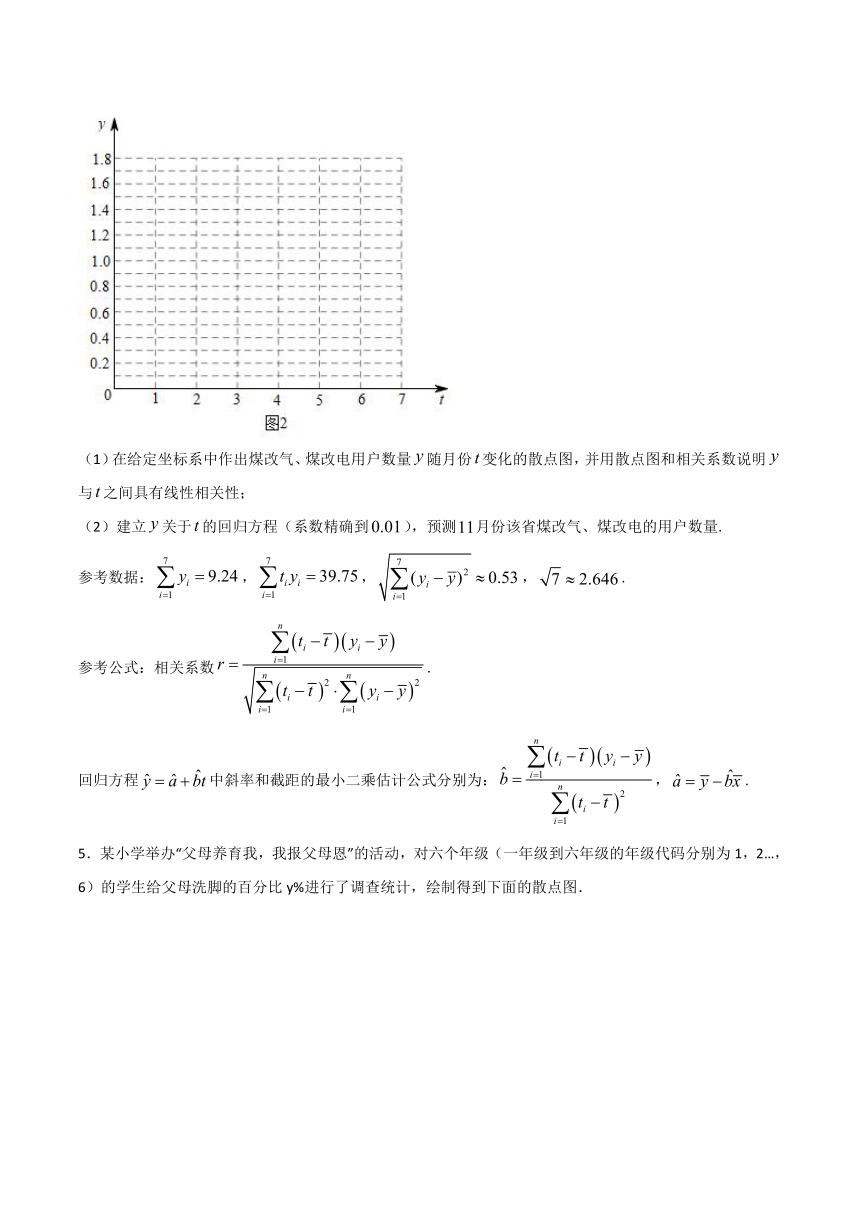
(1)在给定坐标系中作出煤改气、煤改电用户数量false随月份false变化的散点图,并用散点图和相关系数说明false与false之间具有线性相关性;
(2)建立false关于false的回归方程(系数精确到false),预测false月份该省煤改气、煤改电的用户数量.
参考数据:false,false,false,false.
参考公式:相关系数false.
回归方程false中斜率和截距的最小二乘估计公式分别为:false,false.
5.某小学举办“父母养育我,我报父母恩”的活动,对六个年级(一年级到六年级的年级代码分别为1,2…,6)的学生给父母洗脚的百分比y%进行了调查统计,绘制得到下面的散点图.
(1)由散点图看出,可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)建立y关于x的回归方程,并据此预计该校学生升入中学的第一年(年级代码为7)给父母洗脚的百分比.
附注:参考数据:false
参考公式:相关系数false,若r>0.95,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程false中斜率与截距的最小二乘估计公式分别为false=false ,false.
参考答案
1.(1)false;(2)(i)false;(ii)当优等品的尺寸false为false时,收益false的预报值最大.
【详解】
(1)由表可知,抽取的false件合格产品中有false件优等品,
所以,false的所有可能取值为false、false、false、false,
false,false,false,
false,
所以,随机变量false的期望为false;
(2)(i)false,false,
false,false,
false,false,
false,
false,false,所以,false,
故false关于false的回归方程为false;
(ii)由(i)知,false,
false,
当false,即false时,false取得最大值,
故当优等品的尺寸false为false时,收益false的预报值最大.
2.(1)false,可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小;(2)需对当天的生产过程进行检查.
【详解】
(1)由样本数据得false(false)的相关系数为
false
由于false,因此可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小.
(2)由于false,false,
故false的区间范围为false,
由样本数据可以看出抽取的第13个零件的尺寸在false以外,
因此需对当天的生产过程进行检查.
3.(1)false;(2)答案见解析.
【详解】
解:(1)一件产品的质量参数在0.785以上的概率false,
设抽取20件该产品中为合格产品的件数为false,则false,
则false.
(2)false,
同理,false,
false,false,
false
false
false
所以使用时间false与质量参数false之间具有较强的线性相关关系,可用线性回归模型拟合.
4.(1)散点图见解析,false与false的线性相关性相当高;(2)false万户.
【详解】
(1)作出散点图如图所示:
由条形图数据和参考数据得:false,false,false,
false,
false.
false与false的相关系数近似为false,false与false的线性相关性相当高.
(2)由false及(1)得:false,
false,false关于false的回归方程为false;
将false代入回归方程得:false,
false预测false月份该省煤改气、煤改电的用户数量达到false万户.
5.(1)详见解析;(2)见解析.
【详解】
(1)因为false
所以false,
所以false,
因为false所以false,
所以false
由于false与false的相关系数约为false,说明false与false的线性相关程度相当高,从而可用线性回归模型拟合false与false的关系.
(2)false
因为false,所以false
所以回归方程为false
将false,代入回归方程可得false,
所以预计该校学生升入中学的第一年给父母洗脚的百分比为false.
第八章 成对数据的统计分析
8.1成对数据的统计相关性
8.1成对数据的统计相关性
知识梳理
知识梳理
知识点1. 变量的相关关系
相关关系:两个变量________关系,但又________确切到可由其中的一个去精确地决定另一个的程度,这种关系称为________关系.
相关关系的分类
按变量间的增减性分为________相关和________相关.
①正相关:当一个变量的值________时,另一个变量的相应值也________
②负相关:当一个变量的值________时,另一个变量的相应值也________
按变量间是否有线性特征分为线性相关和非线性相关(曲线相关).
①线性相关:如果两个变量的取值呈现________相关或________相关,而且散点落在一条直线附近,我们称这两个变量________相关;
②非线性相关或曲线相关:如果两个变量具有________性,但不是线性相关,我们称这两个变量非线性相关
知识点2.相关关系的刻画
散点图::将样本中的每一个序号下的________样本数据都用直角坐标系中的点表示出来,由这些点组成的统计图叫做________.
样本相关系数
(1)我们常用样本相关系数r来确切地反映成对样本数据(xi,yi)的相关程度,其中r=.
(2)样本相关系数r的取值范围为[-1,1].
①若________时,成对样本数据正相关;
②若________时,成对样本数据负相关;
③当|r|越接近1时,成对样本数据的线性相关程度________;
④当|r|越接近0时,成对样本数据的线性相关程度________.
课后小练
课后小练
1.某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量false与尺寸false之间近似满足关系式false(false、false为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间false内时为优等品.现随机抽取false件合格产品,测得数据如下:
尺寸false
38
48
58
68
78
88
质量false
16.8
18.8
20.7
22.4
24
25.5
质量与尺寸的比false
0.442
0.392
0.357
0.329
0.308
0.290
(1)现从抽取的false件合格产品中再任选false件,记false为取到优等品的件数,试求随机变量false的期望;
(2)根据测得数据作了初步处理,得相关统计量的值如表:
false
false
false
false
false
false
false
false
(i)根据所给统计量,求false关于false的回归方程;
(ii)已知优等品的收益false(单位:千元)与false、false的关系为false,则当优等品的尺寸false为何值时,收益false的预报值最大?
附:对于样本false,其回归直线false的斜率和截距的最小二乘估计公式分别为:false,false,false.
2.商务部会同海关总署?国家药监局于3月31日发布关于有序开展医疗物资出口的公告.如医疗物资出口中出现质量问题,将认真调查,发现一起,查处一起,切实维护“中国制造”的形象,更好地发挥医疗物资对支持全球疫情防控的重要作用.为了监控某种医疗物资的一条生产线的生产过程,检验员每隔30false从该生产线上随机抽取一个医疗物资,并测量其尺寸(单位:false).下面是检验员在一天内依次抽取的16个医疗物资的尺寸:
抽取次数
1
2
3
4
5
6
7
8
医疗物资尺寸
false
false
false
false
false
false
false
false
抽取次数
9
10
11
12
13
14
15
16
医疗物资尺寸
false
false
false
false
false
false
false
false
经计算得false,false,false,false,false,其中false为抽取的第false个医疗物资的尺寸,false
(1)求false的相关系数false,并回答是否可以认为这一天生产的医疗物资尺寸不随生产过程的进行而系统地变大或变小(若false,则可以认为医疗物资尺寸不随生产过程的进行而系统地变大或变小).
(2)一天内抽检医疗物资中,如果出现了尺寸在false之外的医疗物资,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.从这一天抽检的结果看,是否需对当天的生产过程进行检查?
附:样本false的相关系数false
3.某地一公司的市场研究人员为了解公司生产的某产品的使用情况,从两个方面进行了调查统计,一是产品的质量参数x,二是产品的使用时间t(单位:千小时),经统计分析,质量参数x服从正态分布false,使用时间t与质量参数x之间有如下关系:
质量参数x
0.65
0.70
0.75
0.80
0.85
0.90
0.95
使用时间t
2.60
2.81
3.05
3.10
3.25
3.35
3.54
(1)该地监管部门对该公司的该产品进行检查,要求质量参数在0.785以上的产品为合格产品.现抽取20件该产品进行校验,求合格产品的件数的数学期望;
(2)该公司研究人员根据最小二乘法求得线性回归方程为false,请用相关系数说明使用时间t与质量参数x之间的关系是否可用线性回归模型拟合.
附:参考数据:false.若false,则false
参考公式:相关系数false;
回归直线方程为false,其中false.
4.我国北方广大农村地区、一些城镇以及部分大中城市的周边区域,还在大量采用分散燃煤和散烧煤取暖,既影响了居民基本生活的改善,也加重了北方地区冬季的雾霾天气.推进北方地区冬季清洁取暖,是重大民生工程、民心工程,关系北方地区广大群众温暖过冬,关系雾霾天能不能减少,是能源生产和消费革命、农村生活方式革命的重要内容.2017年9月国家发改委制定了煤改气、煤改电价格扶植新政策,从而使得煤改气、煤改电用户大幅度增加,下面条形图反映了某省2018年1~7月份煤改气、煤改电的用户数量.
(1)在给定坐标系中作出煤改气、煤改电用户数量false随月份false变化的散点图,并用散点图和相关系数说明false与false之间具有线性相关性;
(2)建立false关于false的回归方程(系数精确到false),预测false月份该省煤改气、煤改电的用户数量.
参考数据:false,false,false,false.
参考公式:相关系数false.
回归方程false中斜率和截距的最小二乘估计公式分别为:false,false.
5.某小学举办“父母养育我,我报父母恩”的活动,对六个年级(一年级到六年级的年级代码分别为1,2…,6)的学生给父母洗脚的百分比y%进行了调查统计,绘制得到下面的散点图.
(1)由散点图看出,可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)建立y关于x的回归方程,并据此预计该校学生升入中学的第一年(年级代码为7)给父母洗脚的百分比.
附注:参考数据:false
参考公式:相关系数false,若r>0.95,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程false中斜率与截距的最小二乘估计公式分别为false=false ,false.
参考答案
1.(1)false;(2)(i)false;(ii)当优等品的尺寸false为false时,收益false的预报值最大.
【详解】
(1)由表可知,抽取的false件合格产品中有false件优等品,
所以,false的所有可能取值为false、false、false、false,
false,false,false,
false,
所以,随机变量false的期望为false;
(2)(i)false,false,
false,false,
false,false,
false,
false,false,所以,false,
故false关于false的回归方程为false;
(ii)由(i)知,false,
false,
当false,即false时,false取得最大值,
故当优等品的尺寸false为false时,收益false的预报值最大.
2.(1)false,可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小;(2)需对当天的生产过程进行检查.
【详解】
(1)由样本数据得false(false)的相关系数为
false
由于false,因此可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小.
(2)由于false,false,
故false的区间范围为false,
由样本数据可以看出抽取的第13个零件的尺寸在false以外,
因此需对当天的生产过程进行检查.
3.(1)false;(2)答案见解析.
【详解】
解:(1)一件产品的质量参数在0.785以上的概率false,
设抽取20件该产品中为合格产品的件数为false,则false,
则false.
(2)false,
同理,false,
false,false,
false
false
false
所以使用时间false与质量参数false之间具有较强的线性相关关系,可用线性回归模型拟合.
4.(1)散点图见解析,false与false的线性相关性相当高;(2)false万户.
【详解】
(1)作出散点图如图所示:
由条形图数据和参考数据得:false,false,false,
false,
false.
false与false的相关系数近似为false,false与false的线性相关性相当高.
(2)由false及(1)得:false,
false,false关于false的回归方程为false;
将false代入回归方程得:false,
false预测false月份该省煤改气、煤改电的用户数量达到false万户.
5.(1)详见解析;(2)见解析.
【详解】
(1)因为false
所以false,
所以false,
因为false所以false,
所以false
由于false与false的相关系数约为false,说明false与false的线性相关程度相当高,从而可用线性回归模型拟合false与false的关系.
(2)false
因为false,所以false
所以回归方程为false
将false,代入回归方程可得false,
所以预计该校学生升入中学的第一年给父母洗脚的百分比为false.
