第八章 成对数据的统计分析 学案-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(word含答案)
文档属性
| 名称 | 第八章 成对数据的统计分析 学案-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 152.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-09 00:00:00 | ||
图片预览


文档简介
1024890011874500第八章 成对数据的统计分析
第八章 成对数据的统计分析
基础知识
基础知识
知识点1.列联表
(1).2×2列联表给出了________分类变量数据的交叉分类频数.
(2).定义一对分类变量X和Y,我们整理数据如下表所示:
X
Y
合计
Y=0
Y=1
X=0
a
b
________
X=1
c
d
c+d
合计
a+c
b+d
n=________________
像这种形式的数据统计表称为2×2列联表.
知识点2.独立性检验解决实际问题的主要环节
(1)提出零假设H0:X和Y相互________,并给出在问题中的解释.
(2)根据抽样数据整理出2×2列联表,计算χ2的值,并与临界值xα比较.
(3)根据检验规则得出推断结论.
(4)在X和Y不________的情况下,根据需要,通过比较相应的频率,分析X和Y间的影响规律.
知识点3.相关关系的分类
按变量间的增减性分为正相关和负相关.
①正相关:当一个变量的值________时,另一个变量的相应值也________
②负相关:当一个变量的值________时,另一个变量的相应值也________
按变量间是否有线性特征分为线性相关和非线性相关(曲线相关).
①线性相关:如果两个变量的取值呈现________相关或________相关,而且散点落在一条直线附近,我们称这两个变量________相关;
②非线性相关或曲线相关:如果两个变量具有________性,但不是________相关,我们称这两个变量非线性相关
知识点4.一元线性回归模型
称为Y关于x的一元线性回归模型.其中Y称为________或________变量,x称为自变量或解释变量,a称为________参数,b称为________参数;e是Y与bx+a之间的随机误差,如e=0,那么Y与x之间的关系就可以用一元线性函数模型来描述.
知识点5.对模型刻画数据效果的分析
残差图法
残差图中,如残差比较________地集中在以横轴为对称轴的水平带状区域内,说明经验回归方程较好地刻画两个变量的关系.
残差平方和法
残差平方和(yi-i)2越________,模型的拟合效果越好.
课后小练
课后小练
1.某种机械设备随着使用年限的增加,它的使用功能逐渐减退,使用价值逐年减少,通常把它使用价值逐年减少的“量”换算成费用,称之为“失效费”.某种机械设备的使用年限 x (单位:年)与失效费 y (单位:万元)的统计数据如下表所示:
使用年限 x (单位:年)
1
2
3
4
5
6
7
失效费 y (单位:万元)
2.90
3.30
3.60
4.40
4.80
5.20
5.90
(Ⅰ)由上表数据可知,可用线性回归模型拟合 y 与 x 的关系.请用相关系数加以说明;(精确到0.01)
(Ⅱ)求出 y 关于 x 的线性回归方程,并估算该种机械设备使用10年的失效费.
参考公式:相关系数 r=i=1n(xi?x)(yi?y)i=1n(xi?x)2i=1n(yi?y)2 .
线性回归方程 y=bx+a 中斜率和截距最小二乘估计计算公式: b=i=1n(xi?x)(yi?y)i=1n(xi?x)2 , a=y?bx .
参考数据: i=17(xi?x)(yi?y)=14.00 , i=17(yi?y)2=7.08 , 198.24≈14.10 .
2.垃圾分类收集处理是一项利国利民的社会工程和环保工程.搞好垃圾分类收集处理,可为政府节省开支,为国家节约能源,减少环境污染,是建设资源节约型社会的一个重要内容.为推进垃圾分类收集处理工作,A市通过多种渠道对市民进行垃圾分类收集处理方法的宣传教育,为了解市民能否正确进行垃圾分类处理,调查机构借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到如下列联表(单位:人):
能正确进行垃圾分类
不能正确进行垃圾分类
总计
55岁及以下
90
30
120
55岁以上
50
30
80
总计
140
60
200
附: K2=n(ad?bc)2(a+b)(c+d)(a+c)(b+d) ,其中 n=a+b+c+d .
P(K2≥k0)
0.15
0.10
0.05
0.025
k0
2.072
2.706
3.841
5.024
(1)根据以上数据,判断是否有90%的把握认为A市能否正确进行垃圾分类处理与年龄有关?
(2)将频率视为概率,现从A市55岁及以下的市民中用随机抽样的方法每次抽取1人,共抽取3次.记被抽取的3人中“不能正确进行垃圾分类”的人数为 X ,若每次抽取的结果是相互独立的,求随机变量 X 的分布列和均值 E(X) .
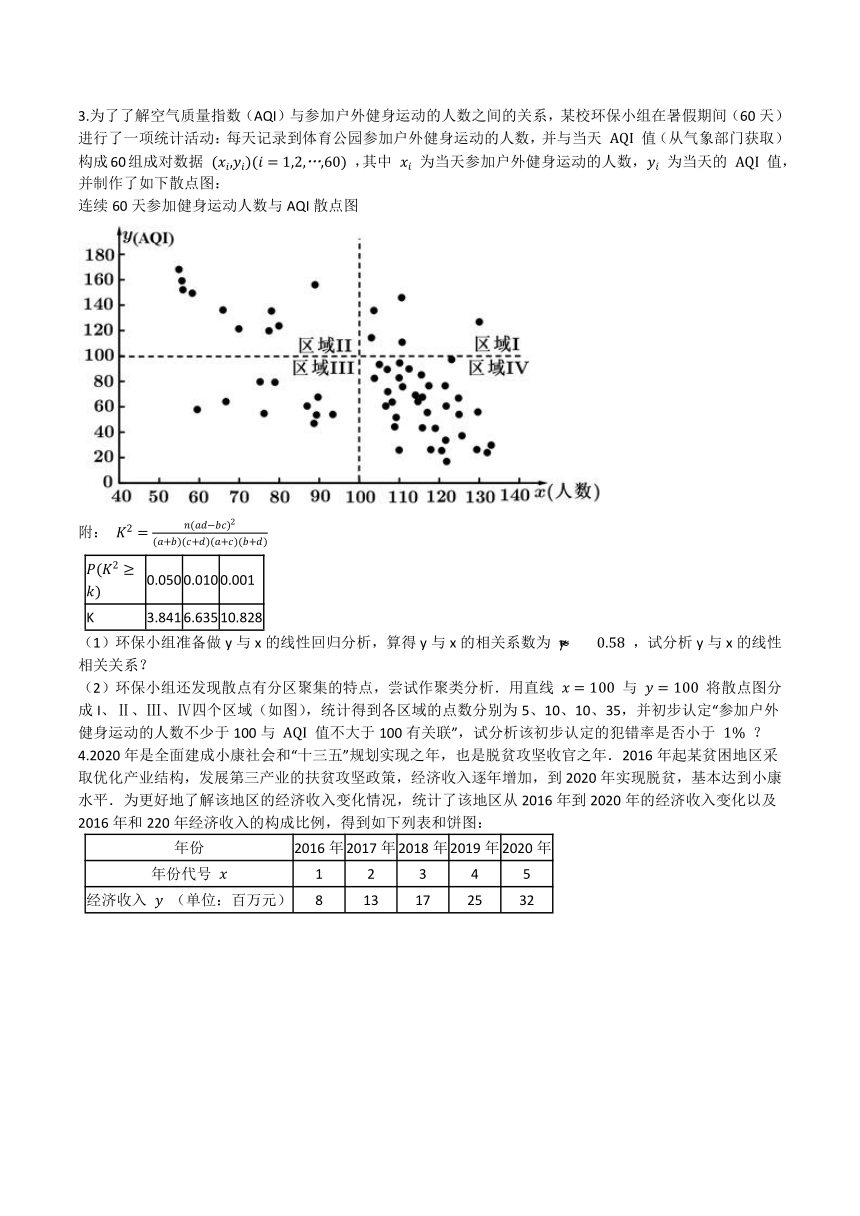
3.为了了解空气质量指数(AQI)与参加户外健身运动的人数之间的关系,某校环保小组在暑假期间(60天)进行了一项统计活动:每天记录到体育公园参加户外健身运动的人数,并与当天 AQI 值(从气象部门获取)构成60组成对数据 (xi,yi)(i=1,2,…,60) ,其中 xi 为当天参加户外健身运动的人数, yi 为当天的 AQI 值,并制作了如下散点图:
连续60天参加健身运动人数与AQI散点图
附: K2=n(ad?bc)2(a+b)(c+d)(a+c)(b+d)
P(K2≥k)
0.050
0.010
0.001
K
3.841
6.635
10.828
(1)环保小组准备做y与x的线性回归分析,算得y与x的相关系数为 γ≈?0.58 ,试分析y与x的线性相关关系?
(2)环保小组还发现散点有分区聚集的特点,尝试作聚类分析.用直线 x=100 与 y=100 将散点图分成I、Ⅱ、Ⅲ、Ⅳ四个区域(如图),统计得到各区域的点数分别为5、10、10、35,并初步认定“参加户外健身运动的人数不少于100与 AQI 值不大于100有关联”,试分析该初步认定的犯错率是否小于 1% ?
4.2020年是全面建成小康社会和“十三五”规划实现之年,也是脱贫攻坚收官之年.2016年起某贫困地区采取优化产业结构,发展第三产业的扶贫攻坚政策,经济收入逐年增加,到2020年实现脱贫,基本达到小康水平.为更好地了解该地区的经济收入变化情况,统计了该地区从2016年到2020年的经济收入变化以及2016年和220年经济收入的构成比例,得到如下列表和饼图:
年份
2016年
2017年
2018年
2019年
2020年
年份代号 x
1
2
3
4
5
经济收入 y (单位:百万元)
8
13
17
25
32
参考公式:对于一组具有线性相关关系的数据 (xi,yi)(i=1,2,3,???,n) ,其回归直线 y=bx+a 的斜率和截距的最小二乘估计分别为: b=i=1n(xi?x)(yi?y)i=1n(xi?x)2 , a=y?bx .
(1)若该地区第三产业收入2020年是2016年的20倍,求2020年经济收入中第三产业收入和其他收入所占百分比 m , n 的值;
(2)求经济收入 y 关于 x 的线性回归方程,并预测2025年该地区的经济收入.
5.某网络购物平台每年11月11日举行“双十一”购物节,当天有多项优惠活动,深受广大消费者喜爱.已知该网络购物平台近5年“双十一”购物当天成交额如下表:
年份
2015
2016
2017
2018
2019
成交额(百亿元)
9
12
17
21
27
参考公式: b=i=1n(xi?x)(yi?y)i=1n(xi?x)2=i=1nxiyi?nxyi=1nxi2?nx2,a=y?bx .
(1)求成交额 y (百亿元)与时间变量 x (记2015年为 x=1 ,2016年为 x=2 ,…以此类推)的线性回归方程;
(2)试预测2021年该平台“双十一”购物当天的成交额(百亿元).
答案解析
1.【答案】 解:(Ⅰ)由题意,知 x=1+2+3+4+5+6+77=4 , y=2.90+3.30+3.60+4.40+4.80+5.20+5.907=4.30 ,
i=17(xi?x)2=(1?4)2+(2?4)2+(3?4)2+(4?4)2+(5?4)2+(6?4)2+(7?4)2=28 .
∴结合参考数据知: r=14.0028×7.08=14.00198.24≈14.0014.10≈0.99 .
因为 y 与 x 的相关系数近似为0.99,所以 y 与 x 的线性相关程度相当大,从而可以用线性回归模型拟合 y 与 x 的关系.
(Ⅱ)∵ b=i=17(xi?x)(yi?y)i=17(xi?x)2=1428=0.5 ,
∴ a=y?bx=4.3?0.5×4=2.3 .
∴ y 关于 x 的线性回归方程为 y=0.5x+2.3 ,将 x=10 代入线性回归方程,得 y=0.5×10+2.3=7.3 .
∴估算该种机械设备使用10年的失效费为7.3万元.
2.【答案】 (1)解:由列联表可知 K2=200×(90×30?50×30)2140×60×80×120≈3.571 ,
因为 3.571>2.706 ,
所以有90%的把握认为A市能否正确进行垃圾分类处理与年龄有关
(2)解:由题意可知,从该市55岁及以下的市民中用随机抽样的方法每次抽取1人,
不能正确进行垃圾分类的频率为 14 ,
所以 X?B(3,14) , X 的所有可能取值为0,1,2,3,
P(X=0)=C30×(34)3=2764 ,
P(X=1)=C31×14×(34)2=2764 ,
P(X=2)=C32×(14)2×34=964 ,
P(X=3)=C33×(14)3=164 ,
所以 X 的分布列为
X
0
1
2
3
P
2764
2764
964
164
所以 E(X)=3×14=34
3.【答案】 (1)解: γ≈?0.58 ,y与x的相关关系为负相关,
且 |γ|<0.75 ,故线性相关性不强,所以不建议继续做线性回归分析,
得到回归方程,拟合效果也会不理想
(2)解:建立2×2列联表如下
人数 <100
人数 ≥100
合计
AQI>100
10
5
15
AQI≤100
10
35
45
合计
20
40
60
代入公式计算得 K2=60×(350?50)215×45×20×40=10
查表知 6.635<10<10.828 ,故犯错率在0.001与0.01之间,
所以该初步认定的犯错率小于 1% .
4.【答案】 (1)解:由表格及饼图可得: m×32=20×8×6% ,
解得 m=30% , n=1?34%?30%?30%=6%
(2)解:由表格数据可得: x=15(1+2+3+4+5)=3 , y=15(8+13+17+25+32)=19 , i=15xi2=12+22+32+42+52=55 , i=15xiyi=1×8+2×13+3×17+4×25+5×32=345
则 b=i=1n(xi?x)(yi?y)i=1n(xi?x)2=i=1nxiyi?nxyi=1nxi2?nx2=345?5×3×1955?5×32=6 ,
a=y?bx=1 ,则经济收入 y 关于 x 的线性回归方程为 y=6x+1 ,
当 x=10 时, y=61 ,则2025年时该地区的经济收入大约为陆仟壹百万元
5.【答案】 (1)解:由已知得: x=1+2+3+4+55=3 , y=9+12+17+21+275=17.2 ,
i=15xiyi=1×9+2×12+3×17+4×21+5×27=303 ,
i=15xi2=12+22+32+42+52=55 ,
所以 b=i=15xiyi?5x?yi=15xi2?5x2=303?5×3×17.255?5×32=4.5 ,
则 a=y?bx=17.2?4.5×3=3.7 ,
所以 y=bx+a=4.5x+3.7 ;
(2)解:以题意可知2021年为 x=7 ,当 x=7 时, y=4.5×7+3.7=35.2 (百亿元)
所以估计2021年该平台“双十一”购物当天的成交额为35.2(百亿元).
第八章 成对数据的统计分析
基础知识
基础知识
知识点1.列联表
(1).2×2列联表给出了________分类变量数据的交叉分类频数.
(2).定义一对分类变量X和Y,我们整理数据如下表所示:
X
Y
合计
Y=0
Y=1
X=0
a
b
________
X=1
c
d
c+d
合计
a+c
b+d
n=________________
像这种形式的数据统计表称为2×2列联表.
知识点2.独立性检验解决实际问题的主要环节
(1)提出零假设H0:X和Y相互________,并给出在问题中的解释.
(2)根据抽样数据整理出2×2列联表,计算χ2的值,并与临界值xα比较.
(3)根据检验规则得出推断结论.
(4)在X和Y不________的情况下,根据需要,通过比较相应的频率,分析X和Y间的影响规律.
知识点3.相关关系的分类
按变量间的增减性分为正相关和负相关.
①正相关:当一个变量的值________时,另一个变量的相应值也________
②负相关:当一个变量的值________时,另一个变量的相应值也________
按变量间是否有线性特征分为线性相关和非线性相关(曲线相关).
①线性相关:如果两个变量的取值呈现________相关或________相关,而且散点落在一条直线附近,我们称这两个变量________相关;
②非线性相关或曲线相关:如果两个变量具有________性,但不是________相关,我们称这两个变量非线性相关
知识点4.一元线性回归模型
称为Y关于x的一元线性回归模型.其中Y称为________或________变量,x称为自变量或解释变量,a称为________参数,b称为________参数;e是Y与bx+a之间的随机误差,如e=0,那么Y与x之间的关系就可以用一元线性函数模型来描述.
知识点5.对模型刻画数据效果的分析
残差图法
残差图中,如残差比较________地集中在以横轴为对称轴的水平带状区域内,说明经验回归方程较好地刻画两个变量的关系.
残差平方和法
残差平方和(yi-i)2越________,模型的拟合效果越好.
课后小练
课后小练
1.某种机械设备随着使用年限的增加,它的使用功能逐渐减退,使用价值逐年减少,通常把它使用价值逐年减少的“量”换算成费用,称之为“失效费”.某种机械设备的使用年限 x (单位:年)与失效费 y (单位:万元)的统计数据如下表所示:
使用年限 x (单位:年)
1
2
3
4
5
6
7
失效费 y (单位:万元)
2.90
3.30
3.60
4.40
4.80
5.20
5.90
(Ⅰ)由上表数据可知,可用线性回归模型拟合 y 与 x 的关系.请用相关系数加以说明;(精确到0.01)
(Ⅱ)求出 y 关于 x 的线性回归方程,并估算该种机械设备使用10年的失效费.
参考公式:相关系数 r=i=1n(xi?x)(yi?y)i=1n(xi?x)2i=1n(yi?y)2 .
线性回归方程 y=bx+a 中斜率和截距最小二乘估计计算公式: b=i=1n(xi?x)(yi?y)i=1n(xi?x)2 , a=y?bx .
参考数据: i=17(xi?x)(yi?y)=14.00 , i=17(yi?y)2=7.08 , 198.24≈14.10 .
2.垃圾分类收集处理是一项利国利民的社会工程和环保工程.搞好垃圾分类收集处理,可为政府节省开支,为国家节约能源,减少环境污染,是建设资源节约型社会的一个重要内容.为推进垃圾分类收集处理工作,A市通过多种渠道对市民进行垃圾分类收集处理方法的宣传教育,为了解市民能否正确进行垃圾分类处理,调查机构借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到如下列联表(单位:人):
能正确进行垃圾分类
不能正确进行垃圾分类
总计
55岁及以下
90
30
120
55岁以上
50
30
80
总计
140
60
200
附: K2=n(ad?bc)2(a+b)(c+d)(a+c)(b+d) ,其中 n=a+b+c+d .
P(K2≥k0)
0.15
0.10
0.05
0.025
k0
2.072
2.706
3.841
5.024
(1)根据以上数据,判断是否有90%的把握认为A市能否正确进行垃圾分类处理与年龄有关?
(2)将频率视为概率,现从A市55岁及以下的市民中用随机抽样的方法每次抽取1人,共抽取3次.记被抽取的3人中“不能正确进行垃圾分类”的人数为 X ,若每次抽取的结果是相互独立的,求随机变量 X 的分布列和均值 E(X) .
3.为了了解空气质量指数(AQI)与参加户外健身运动的人数之间的关系,某校环保小组在暑假期间(60天)进行了一项统计活动:每天记录到体育公园参加户外健身运动的人数,并与当天 AQI 值(从气象部门获取)构成60组成对数据 (xi,yi)(i=1,2,…,60) ,其中 xi 为当天参加户外健身运动的人数, yi 为当天的 AQI 值,并制作了如下散点图:
连续60天参加健身运动人数与AQI散点图
附: K2=n(ad?bc)2(a+b)(c+d)(a+c)(b+d)
P(K2≥k)
0.050
0.010
0.001
K
3.841
6.635
10.828
(1)环保小组准备做y与x的线性回归分析,算得y与x的相关系数为 γ≈?0.58 ,试分析y与x的线性相关关系?
(2)环保小组还发现散点有分区聚集的特点,尝试作聚类分析.用直线 x=100 与 y=100 将散点图分成I、Ⅱ、Ⅲ、Ⅳ四个区域(如图),统计得到各区域的点数分别为5、10、10、35,并初步认定“参加户外健身运动的人数不少于100与 AQI 值不大于100有关联”,试分析该初步认定的犯错率是否小于 1% ?
4.2020年是全面建成小康社会和“十三五”规划实现之年,也是脱贫攻坚收官之年.2016年起某贫困地区采取优化产业结构,发展第三产业的扶贫攻坚政策,经济收入逐年增加,到2020年实现脱贫,基本达到小康水平.为更好地了解该地区的经济收入变化情况,统计了该地区从2016年到2020年的经济收入变化以及2016年和220年经济收入的构成比例,得到如下列表和饼图:
年份
2016年
2017年
2018年
2019年
2020年
年份代号 x
1
2
3
4
5
经济收入 y (单位:百万元)
8
13
17
25
32
参考公式:对于一组具有线性相关关系的数据 (xi,yi)(i=1,2,3,???,n) ,其回归直线 y=bx+a 的斜率和截距的最小二乘估计分别为: b=i=1n(xi?x)(yi?y)i=1n(xi?x)2 , a=y?bx .
(1)若该地区第三产业收入2020年是2016年的20倍,求2020年经济收入中第三产业收入和其他收入所占百分比 m , n 的值;
(2)求经济收入 y 关于 x 的线性回归方程,并预测2025年该地区的经济收入.
5.某网络购物平台每年11月11日举行“双十一”购物节,当天有多项优惠活动,深受广大消费者喜爱.已知该网络购物平台近5年“双十一”购物当天成交额如下表:
年份
2015
2016
2017
2018
2019
成交额(百亿元)
9
12
17
21
27
参考公式: b=i=1n(xi?x)(yi?y)i=1n(xi?x)2=i=1nxiyi?nxyi=1nxi2?nx2,a=y?bx .
(1)求成交额 y (百亿元)与时间变量 x (记2015年为 x=1 ,2016年为 x=2 ,…以此类推)的线性回归方程;
(2)试预测2021年该平台“双十一”购物当天的成交额(百亿元).
答案解析
1.【答案】 解:(Ⅰ)由题意,知 x=1+2+3+4+5+6+77=4 , y=2.90+3.30+3.60+4.40+4.80+5.20+5.907=4.30 ,
i=17(xi?x)2=(1?4)2+(2?4)2+(3?4)2+(4?4)2+(5?4)2+(6?4)2+(7?4)2=28 .
∴结合参考数据知: r=14.0028×7.08=14.00198.24≈14.0014.10≈0.99 .
因为 y 与 x 的相关系数近似为0.99,所以 y 与 x 的线性相关程度相当大,从而可以用线性回归模型拟合 y 与 x 的关系.
(Ⅱ)∵ b=i=17(xi?x)(yi?y)i=17(xi?x)2=1428=0.5 ,
∴ a=y?bx=4.3?0.5×4=2.3 .
∴ y 关于 x 的线性回归方程为 y=0.5x+2.3 ,将 x=10 代入线性回归方程,得 y=0.5×10+2.3=7.3 .
∴估算该种机械设备使用10年的失效费为7.3万元.
2.【答案】 (1)解:由列联表可知 K2=200×(90×30?50×30)2140×60×80×120≈3.571 ,
因为 3.571>2.706 ,
所以有90%的把握认为A市能否正确进行垃圾分类处理与年龄有关
(2)解:由题意可知,从该市55岁及以下的市民中用随机抽样的方法每次抽取1人,
不能正确进行垃圾分类的频率为 14 ,
所以 X?B(3,14) , X 的所有可能取值为0,1,2,3,
P(X=0)=C30×(34)3=2764 ,
P(X=1)=C31×14×(34)2=2764 ,
P(X=2)=C32×(14)2×34=964 ,
P(X=3)=C33×(14)3=164 ,
所以 X 的分布列为
X
0
1
2
3
P
2764
2764
964
164
所以 E(X)=3×14=34
3.【答案】 (1)解: γ≈?0.58 ,y与x的相关关系为负相关,
且 |γ|<0.75 ,故线性相关性不强,所以不建议继续做线性回归分析,
得到回归方程,拟合效果也会不理想
(2)解:建立2×2列联表如下
人数 <100
人数 ≥100
合计
AQI>100
10
5
15
AQI≤100
10
35
45
合计
20
40
60
代入公式计算得 K2=60×(350?50)215×45×20×40=10
查表知 6.635<10<10.828 ,故犯错率在0.001与0.01之间,
所以该初步认定的犯错率小于 1% .
4.【答案】 (1)解:由表格及饼图可得: m×32=20×8×6% ,
解得 m=30% , n=1?34%?30%?30%=6%
(2)解:由表格数据可得: x=15(1+2+3+4+5)=3 , y=15(8+13+17+25+32)=19 , i=15xi2=12+22+32+42+52=55 , i=15xiyi=1×8+2×13+3×17+4×25+5×32=345
则 b=i=1n(xi?x)(yi?y)i=1n(xi?x)2=i=1nxiyi?nxyi=1nxi2?nx2=345?5×3×1955?5×32=6 ,
a=y?bx=1 ,则经济收入 y 关于 x 的线性回归方程为 y=6x+1 ,
当 x=10 时, y=61 ,则2025年时该地区的经济收入大约为陆仟壹百万元
5.【答案】 (1)解:由已知得: x=1+2+3+4+55=3 , y=9+12+17+21+275=17.2 ,
i=15xiyi=1×9+2×12+3×17+4×21+5×27=303 ,
i=15xi2=12+22+32+42+52=55 ,
所以 b=i=15xiyi?5x?yi=15xi2?5x2=303?5×3×17.255?5×32=4.5 ,
则 a=y?bx=17.2?4.5×3=3.7 ,
所以 y=bx+a=4.5x+3.7 ;
(2)解:以题意可知2021年为 x=7 ,当 x=7 时, y=4.5×7+3.7=35.2 (百亿元)
所以估计2021年该平台“双十一”购物当天的成交额为35.2(百亿元).
