7.4 二项分布与超几何分布 学案-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(wordl含答案)
文档属性
| 名称 | 7.4 二项分布与超几何分布 学案-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(wordl含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 443.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-09 00:00:00 | ||
图片预览



文档简介
第七章 随机变量及其分布
第七章 随机变量及其分布
7.4二项分布与超几何分布
7.4二项分布与超几何分布
知识梳理
知识梳理
知识点一n重伯努利试验及其特征
1.n重伯努利试验的概念
将一个伯努利试验独立地________进行n次所组成的随机试验称为n重伯努利试验.
2.n重伯努利试验的共同特征
(1)同一个伯努利试验________做n次.
(2)各次试验的结果________________.
知识点二:二项分布
一般地,在n重伯努利试验中,设每次试验中事件A发生的概率为p(0 P(X=k)=________________,k=0,1,2,…,n.
称随机变量X服从二项分布,记作________________
知识点三 二项分布的均值与方差
二项分布的均值与方差
(1)二项分布的均值:在n次独立重复试验中,若X~B(n,p),则________________
二项分布的方差:若离散型随机变量X从二项分布,即X~B(n,p),则D(X)=np(1-p).
知识点四 超几何分布
定义:一般地,假设一批产品共有N件,其中有M件次品,从N件产品中随机抽取n件(不放回),用X表示抽取的n件产品中的次品数,则X的分布列为
(________________________________________________________)
其中n,N,M∈N*,M≤N,n≤N,m=max{0,n-N+M},r=min{n,M}.
如果随机变量X的分布列具有上式的形式,那么称随机变量X服从________________.
超几何分布的均值
设随机变量X服从超几何分布,则X可以解释为从包含M件次品的N件产品中,不放回地随机抽取n件产品中的次品数.令p=MN , 则p是N件产品的次品率,而是抽取的 n件产品的次品率,则E( Xn )=p,即________________
课后小练
课后小练
1.2020年第七次全国人口普查摸底工作从10月11日开始,10月31日结束.从11月1日开始进入普查的正式登记阶段.普查员进入每个住户逐人逐项登记普查信息,这期间还将随机抽取false的住户填报普查长表,调查更为详细的人口结构信息.整个登记工作持续到12月10日结束.某社区对随机抽取的false住户普查长表信息情况汇总,并按照住户人均年收入情况绘制出如下的频率分布直方图(假设该社区内住户人均年收人均在0到12万之间.):
(1)若抽取的false住户中,家庭人均年收人在false万元的恰好有32户,则该社区共有住户约多少户.
(2)若从抽取的false住户中人均年收人不高于8万元的住户中按照分层抽样的方法抽取10户,再从这10户中随机抽取4户对其住房和医疗保健情况进行调查,用X表示抽取的4户中家庭收入不少于6万元的住户数,求随机变量X的分布列与数学期望.
2.核酸检测是诊断新冠肺炎的重要依据,首先取病人的唾液或咽拭子的样本,再提取唾液或咽拭子样本里的遗传物质,如果有病毒,样本检测会呈现阳性,否则为阴性.多个样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验,混合样本中只要有病毒,则混合样本化验结果就会呈阳性,若混合样本呈阳性,则将该组中各个样本再逐个化验:若混合样本呈阴性,则该组各个样本均为阴性.根据统计发现,疑似病例核酸检测呈阳性的概率为false.现用两种方案对4例疑似病例进行核酸检测.
(1)方案一:4例逐个化验,设检测结果呈阳性的人数为X,求X的概率分布列;
(2)方案二:4例平均分成两组化验,设需要检测的次数为Y,求Y的概率分布列.
3.某企业对生产设备进行优化升级,升级后的设备控制系统由false个相同的元件组成,每个元件正常工作的概率均为false,各元件之间相互独立.当控制系统有不少于false个元件正常工作时,设备正常运行,否则设备停止运行,记设备正常运行的概率为false(例如:false表示控制系统由3个元件组成时设备正常运行的概率;false表示控制系统由5个元件组成时设备正常运行的概率).
(1)若每个元件正常工作的概率false.
(i)当false时,求控制系统中正常工作的元件个数false的分布列和期望;
(ii)计算false.
(2)已知设备升级前,单位时间的产量为false件,每件产品的利润为1元,设备升级后,在正常运行状态下,单位时间的产量是原来的4倍,且出现了髙端产品,每件产品成为高端产品的概率为false,每件髙端产品的利润是2元.请用false表示出设备升级后单位时间内的利润false(单位:元),在确保控制系统中元件总数为奇数的前提下,分析该设备能否通过增加控制系统中元件的个数来提高利润.
4.《讲课中国行动(2019—2030年)》包括15个专项行动,其中全民健身行动提出鼓励公众每周进行3次以上、每次30分钟以上中等强度运动,或者累计150分钟中等强度75分钟高强度身体活动.日常生活中要尽量多动,达到每天6千步~10千步的身体活动量.某高校从该校教职工中随机抽取了若干名,统计他们的人均步行数(均在2千步~14千步之间),得到的数据如下表:
日均步行数/千步
false
false
false
false
false
false
人数
12
24
false
24
false
9
频率
0.08
0.16
0.4
0.16
false
0.06
(1)求false,false,false的值;
(2)“每天运动一小时,健康工作五十年”,学校为了鼓励教职工积极参与锻炼,决定对日均步行数不低于false千步的教职工进行奖励,为了使全校30%的教职工得到奖励,试估计false的值;
(3)在第(2)问的条件下,以频率作为概率,从该校得到奖励的教职工中随机收取3人,设这3人中日均步行数不低于10千步的人数为false,求false的分布列和数学期望.
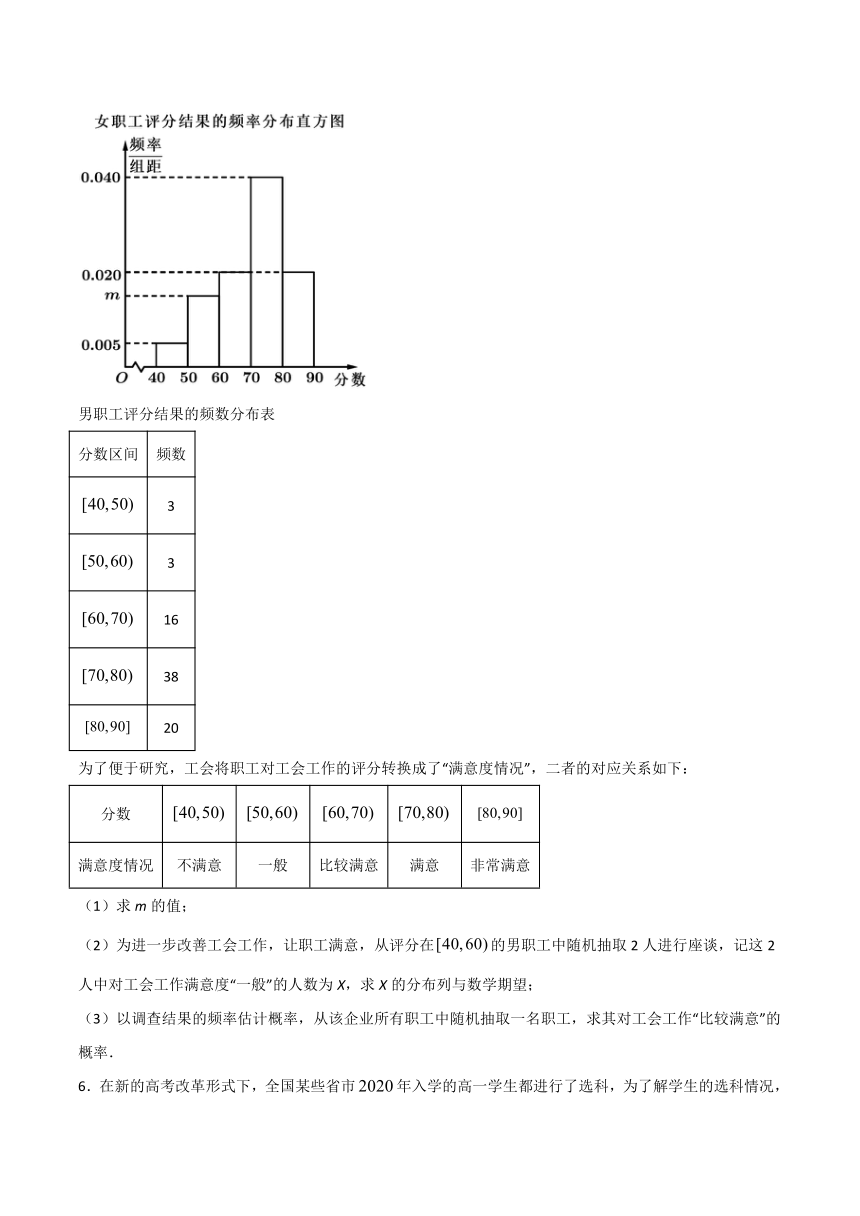
5.为了解企业职工对工会工作满意度情况之间的关系,某企业工会按性别采用分层抽样的方法,从全体企业职工中抽取容量为200的样本进行调查.被抽中的职工分别对工会工作进行评分,满分为100分,调查结果显示:最低分为40分,最高分为90分.随后,企业工会将男、女职工的评分结果按照相同的分组方式分别整理成了频数分布表和频率分布直方图,图表如下:
男职工评分结果的频数分布表
分数区间
频数
false
3
false
3
false
16
false
38
false
20
为了便于研究,工会将职工对工会工作的评分转换成了“满意度情况”,二者的对应关系如下:
分数
false
false
false
false
false
满意度情况
不满意
一般
比较满意
满意
非常满意
(1)求m的值;
(2)为进一步改善工会工作,让职工满意,从评分在false的男职工中随机抽取2人进行座谈,记这2人中对工会工作满意度“一般”的人数为X,求X的分布列与数学期望;
(3)以调查结果的频率估计概率,从该企业所有职工中随机抽取一名职工,求其对工会工作“比较满意”的概率.
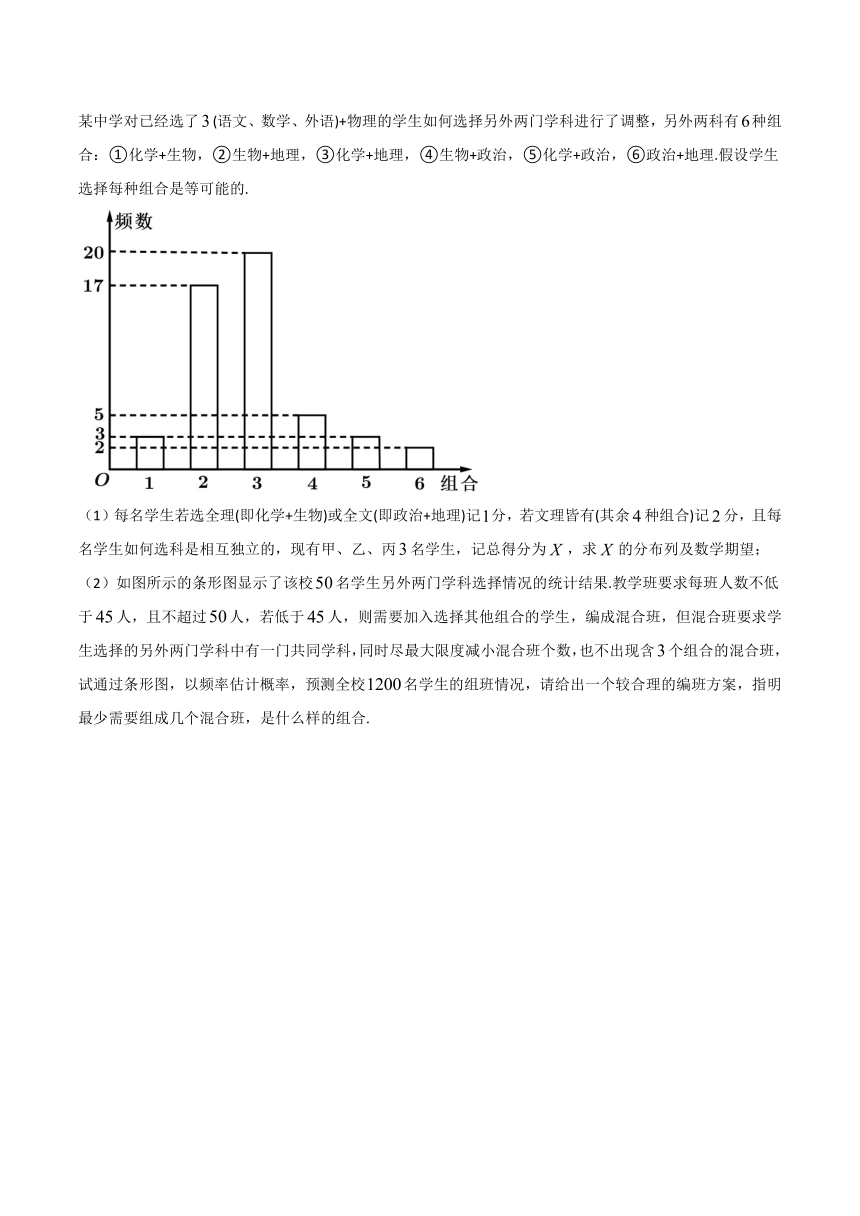
6.在新的高考改革形式下,全国某些省市false年入学的高一学生都进行了选科,为了解学生的选科情况,某中学对已经选了false(语文、数学、外语)+物理的学生如何选择另外两门学科进行了调整,另外两科有false种组合:①化学+生物,②生物+地理,③化学+地理,④生物+政治,⑤化学+政治,⑥政治+地理.假设学生选择每种组合是等可能的.
(1)每名学生若选全理(即化学+生物)或全文(即政治+地理)记false分,若文理皆有(其余false种组合)记false分,且每名学生如何选科是相互独立的,现有甲、乙、丙false名学生,记总得分为false,求false的分布列及数学期望;
(2)如图所示的条形图显示了该校false名学生另外两门学科选择情况的统计结果.教学班要求每班人数不低于false人,且不超过false人,若低于false人,则需要加入选择其他组合的学生,编成混合班,但混合班要求学生选择的另外两门学科中有一门共同学科,同时尽最大限度减小混合班个数,也不出现含false个组合的混合班,试通过条形图,以频率估计概率,预测全校false名学生的组班情况,请给出一个较合理的编班方案,指明最少需要组成几个混合班,是什么样的组合.
参考答案
1.(1)1600户;(2)分布列见解析;期望为false.
【详解】
解:(1)依题意,由频率分布直方图可知,
false,
所以false,
所以抽取的false住户中,家庭人均年收入在false万元的比重恰好为false,又恰好为32户,所有false住户共计约为160户,
进而可得该社区共有住户约1600户.
(2)依题意,在家庭人均年收入不高于8万元的住户中分层抽样抽取10户,
可知10户中,收入在false是1户,false是2户,false是3户,false是4户,
其中不少于6万的占4户,再从这10户中随机抽取4户对其住房和医疗保健情况进行调查,
所有X的可能值为0,1,2,3,4.
所以false,
false;false,
false,
故随机变量X的分布列为:
X
0
1
2
3
4
P
false
false
false
false
false
所以false.
2.(1)答案见解析;(2)答案见解析.
【详解】
(1)方案一false例逐个化验,检测结果呈阳性的人数false,
所以false,
false
false
所以X的分布列为
false
0
1
2
3
4
false
false
false
false
false
false
(2)方案二:4例平均分成两组化验,每一组两个样本检测,
若呈阴性,则检验次数为1,概率为false
若呈阳性,则检验次数为3,概率为false
false
所以false的分布列为
false
2
4
6
false
false
false
false
3.(1)(i)分布列见解析,数学期望为2;(ii)false;(2)false;分类讨论,答案见解析.
【详解】
(1)(i)因为false,所以控制系统中正常工作的元件个数false的可能取值为0,1,2,3;
因为每个元件的工作相互独立,且正常工作的概率均为false,
所以false,
所以false,
false
false,
false,
所以控制系统中正常工作的元件个数false的分布列为
false
0
1
2
3
false
false
false
false
false
控制系统中正常工作的元件个数false的数学期望为false;
(ii)由题意知:
false
false;
(2)升级改造后单位时间内产量的分布列为
产量
false
0
设备运行概率
false
false
所以升级改造后单位时间内产量的期望为false;
所以
产品类型
高端产品
一般产品
产量(单位:件)
false
false
利润(单位:元)
2
1
设备升级后单位时间内的利润为
false,即false;
因为控制系统中元件总数为奇数,若增加2个元件,则第一类:原系统中至少有false个元件正常工作,其概率为false;
第二类:原系统中恰好有false个元件正常工作,新增2个元件中至少有1个正常工作,其概率为
false;
第三类:原系统中有false个元件正常工作,新增2个元件全部正常工作,其概率为
false;
所以false
false,
即false,
所以当false时,false,false单调递增,
即增加元件个数设备正常工作的概率变大,
当false时,false,
即增加元件个数设备正常工作的概率没有变大,
又因为false,
所以当false时,设备可以通过增加控制系统中元件的个数来提高利润;
当false时,设备不可以通过增加控制系统中元件的个数来提高利润.
4.(1)false,false,false;(2)false;(3)分布列见解析,false.
【详解】
(1)由题意得:false,解得:false;false;则false,解得:false.
(2)日均步行数在false内的频率为:false,
日均步行数在false内的频率为false,
则false,解得:false.
false当false时,全校false的教职工能够得到奖励.
(3)由题意知:该校得到奖励的教职工在全校教职工中所占的比例为false,
false日均步行数不低于false千步的教职工在得到奖励的教职工所占的比例为false,false,
false,false,false,false,
false的分布列为:
false
false
false
false
false
false
false
false
false
false
数学期望false.
5.(1)false;(2)分布列见解析,1;(3)false.
【详解】
解:(1)因为false,
所以false.
(2)依题意,随机变量X的所有可能取值为0,1,2.
则false,false,
false.
所以随机变量X的分布列为
X
0
1
2
P
false
false
false
故X的数学期望false.
(3)设事件false{随机抽取一名职工,对工会工作服务“比较满意”}.
因为样本人数200人,其中男职工共有80人,
所以样本中女职工共有120人.
由频率分布直方图可知,
女职工对工会工作服务“比较满意”的人数共有:false人.
由频数分布表,可知男职工对工会工作“比较满意”的共有16人,
所以随机抽取一名职工,对工会工作“比较满意”的概率为false.
6.(1)分布列见解析,false;(2)答案见解析.
【详解】
(1)选全理(即化学+生物)或全文(即政治+地理)的概率为false, 即记false分的概率为false,因而记false分的概率为false,
易知false的可能取值为false、false、false、false,且false,false,false,false,
∴false的分布列为:
false
false
false
false
false
false
false
false
false
false
∴false;
(2)分情况进行讨论:
组合①:false人中选择①的有false人,其频率为false,预测全校false名学生选择①的人数为false,独立成一个班,剩下false人,
组合②:false人中选择②的有false人,其频率为false,预测全校false名学生选择②的人数为false,独立成八个50人的班,剩下false人,
组合③:false人中选择③的有false人,其频率为false,预测全校false名学生选择③的人数为false,独立成十个班,
组合④:false人中选择④的有false人,其频率为false,预测全校false名学生选择④的人数为false,独立成二个班,至少剩下false人,
组合⑤:false人中选择⑤的有false人,其频率为false,预测全校false名学生选择⑤的人数为false,独立成一个班,至少剩下false人,
组合⑥:false人中选择⑥的有false人,其频率为false,预测全校false名学生选择⑥的人数为false,独立成一个班,
①
⑤
②
④
化学+生物
化学+政治
生物+地理
生物+政治
false人
false人
false人
false人
减小混合班个数,把①⑤中独立班的人数调整为47到49人,剩下的学生组合成一个混合班,把②④剩下的学生组合成一个混合班(②组成的独立成八个班中每班减少false人).
第七章 随机变量及其分布
7.4二项分布与超几何分布
7.4二项分布与超几何分布
知识梳理
知识梳理
知识点一n重伯努利试验及其特征
1.n重伯努利试验的概念
将一个伯努利试验独立地________进行n次所组成的随机试验称为n重伯努利试验.
2.n重伯努利试验的共同特征
(1)同一个伯努利试验________做n次.
(2)各次试验的结果________________.
知识点二:二项分布
一般地,在n重伯努利试验中,设每次试验中事件A发生的概率为p(0
称随机变量X服从二项分布,记作________________
知识点三 二项分布的均值与方差
二项分布的均值与方差
(1)二项分布的均值:在n次独立重复试验中,若X~B(n,p),则________________
二项分布的方差:若离散型随机变量X从二项分布,即X~B(n,p),则D(X)=np(1-p).
知识点四 超几何分布
定义:一般地,假设一批产品共有N件,其中有M件次品,从N件产品中随机抽取n件(不放回),用X表示抽取的n件产品中的次品数,则X的分布列为
(________________________________________________________)
其中n,N,M∈N*,M≤N,n≤N,m=max{0,n-N+M},r=min{n,M}.
如果随机变量X的分布列具有上式的形式,那么称随机变量X服从________________.
超几何分布的均值
设随机变量X服从超几何分布,则X可以解释为从包含M件次品的N件产品中,不放回地随机抽取n件产品中的次品数.令p=MN , 则p是N件产品的次品率,而是抽取的 n件产品的次品率,则E( Xn )=p,即________________
课后小练
课后小练
1.2020年第七次全国人口普查摸底工作从10月11日开始,10月31日结束.从11月1日开始进入普查的正式登记阶段.普查员进入每个住户逐人逐项登记普查信息,这期间还将随机抽取false的住户填报普查长表,调查更为详细的人口结构信息.整个登记工作持续到12月10日结束.某社区对随机抽取的false住户普查长表信息情况汇总,并按照住户人均年收入情况绘制出如下的频率分布直方图(假设该社区内住户人均年收人均在0到12万之间.):
(1)若抽取的false住户中,家庭人均年收人在false万元的恰好有32户,则该社区共有住户约多少户.
(2)若从抽取的false住户中人均年收人不高于8万元的住户中按照分层抽样的方法抽取10户,再从这10户中随机抽取4户对其住房和医疗保健情况进行调查,用X表示抽取的4户中家庭收入不少于6万元的住户数,求随机变量X的分布列与数学期望.
2.核酸检测是诊断新冠肺炎的重要依据,首先取病人的唾液或咽拭子的样本,再提取唾液或咽拭子样本里的遗传物质,如果有病毒,样本检测会呈现阳性,否则为阴性.多个样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验,混合样本中只要有病毒,则混合样本化验结果就会呈阳性,若混合样本呈阳性,则将该组中各个样本再逐个化验:若混合样本呈阴性,则该组各个样本均为阴性.根据统计发现,疑似病例核酸检测呈阳性的概率为false.现用两种方案对4例疑似病例进行核酸检测.
(1)方案一:4例逐个化验,设检测结果呈阳性的人数为X,求X的概率分布列;
(2)方案二:4例平均分成两组化验,设需要检测的次数为Y,求Y的概率分布列.
3.某企业对生产设备进行优化升级,升级后的设备控制系统由false个相同的元件组成,每个元件正常工作的概率均为false,各元件之间相互独立.当控制系统有不少于false个元件正常工作时,设备正常运行,否则设备停止运行,记设备正常运行的概率为false(例如:false表示控制系统由3个元件组成时设备正常运行的概率;false表示控制系统由5个元件组成时设备正常运行的概率).
(1)若每个元件正常工作的概率false.
(i)当false时,求控制系统中正常工作的元件个数false的分布列和期望;
(ii)计算false.
(2)已知设备升级前,单位时间的产量为false件,每件产品的利润为1元,设备升级后,在正常运行状态下,单位时间的产量是原来的4倍,且出现了髙端产品,每件产品成为高端产品的概率为false,每件髙端产品的利润是2元.请用false表示出设备升级后单位时间内的利润false(单位:元),在确保控制系统中元件总数为奇数的前提下,分析该设备能否通过增加控制系统中元件的个数来提高利润.
4.《讲课中国行动(2019—2030年)》包括15个专项行动,其中全民健身行动提出鼓励公众每周进行3次以上、每次30分钟以上中等强度运动,或者累计150分钟中等强度75分钟高强度身体活动.日常生活中要尽量多动,达到每天6千步~10千步的身体活动量.某高校从该校教职工中随机抽取了若干名,统计他们的人均步行数(均在2千步~14千步之间),得到的数据如下表:
日均步行数/千步
false
false
false
false
false
false
人数
12
24
false
24
false
9
频率
0.08
0.16
0.4
0.16
false
0.06
(1)求false,false,false的值;
(2)“每天运动一小时,健康工作五十年”,学校为了鼓励教职工积极参与锻炼,决定对日均步行数不低于false千步的教职工进行奖励,为了使全校30%的教职工得到奖励,试估计false的值;
(3)在第(2)问的条件下,以频率作为概率,从该校得到奖励的教职工中随机收取3人,设这3人中日均步行数不低于10千步的人数为false,求false的分布列和数学期望.
5.为了解企业职工对工会工作满意度情况之间的关系,某企业工会按性别采用分层抽样的方法,从全体企业职工中抽取容量为200的样本进行调查.被抽中的职工分别对工会工作进行评分,满分为100分,调查结果显示:最低分为40分,最高分为90分.随后,企业工会将男、女职工的评分结果按照相同的分组方式分别整理成了频数分布表和频率分布直方图,图表如下:
男职工评分结果的频数分布表
分数区间
频数
false
3
false
3
false
16
false
38
false
20
为了便于研究,工会将职工对工会工作的评分转换成了“满意度情况”,二者的对应关系如下:
分数
false
false
false
false
false
满意度情况
不满意
一般
比较满意
满意
非常满意
(1)求m的值;
(2)为进一步改善工会工作,让职工满意,从评分在false的男职工中随机抽取2人进行座谈,记这2人中对工会工作满意度“一般”的人数为X,求X的分布列与数学期望;
(3)以调查结果的频率估计概率,从该企业所有职工中随机抽取一名职工,求其对工会工作“比较满意”的概率.
6.在新的高考改革形式下,全国某些省市false年入学的高一学生都进行了选科,为了解学生的选科情况,某中学对已经选了false(语文、数学、外语)+物理的学生如何选择另外两门学科进行了调整,另外两科有false种组合:①化学+生物,②生物+地理,③化学+地理,④生物+政治,⑤化学+政治,⑥政治+地理.假设学生选择每种组合是等可能的.
(1)每名学生若选全理(即化学+生物)或全文(即政治+地理)记false分,若文理皆有(其余false种组合)记false分,且每名学生如何选科是相互独立的,现有甲、乙、丙false名学生,记总得分为false,求false的分布列及数学期望;
(2)如图所示的条形图显示了该校false名学生另外两门学科选择情况的统计结果.教学班要求每班人数不低于false人,且不超过false人,若低于false人,则需要加入选择其他组合的学生,编成混合班,但混合班要求学生选择的另外两门学科中有一门共同学科,同时尽最大限度减小混合班个数,也不出现含false个组合的混合班,试通过条形图,以频率估计概率,预测全校false名学生的组班情况,请给出一个较合理的编班方案,指明最少需要组成几个混合班,是什么样的组合.
参考答案
1.(1)1600户;(2)分布列见解析;期望为false.
【详解】
解:(1)依题意,由频率分布直方图可知,
false,
所以false,
所以抽取的false住户中,家庭人均年收入在false万元的比重恰好为false,又恰好为32户,所有false住户共计约为160户,
进而可得该社区共有住户约1600户.
(2)依题意,在家庭人均年收入不高于8万元的住户中分层抽样抽取10户,
可知10户中,收入在false是1户,false是2户,false是3户,false是4户,
其中不少于6万的占4户,再从这10户中随机抽取4户对其住房和医疗保健情况进行调查,
所有X的可能值为0,1,2,3,4.
所以false,
false;false,
false,
故随机变量X的分布列为:
X
0
1
2
3
4
P
false
false
false
false
false
所以false.
2.(1)答案见解析;(2)答案见解析.
【详解】
(1)方案一false例逐个化验,检测结果呈阳性的人数false,
所以false,
false
false
所以X的分布列为
false
0
1
2
3
4
false
false
false
false
false
false
(2)方案二:4例平均分成两组化验,每一组两个样本检测,
若呈阴性,则检验次数为1,概率为false
若呈阳性,则检验次数为3,概率为false
false
所以false的分布列为
false
2
4
6
false
false
false
false
3.(1)(i)分布列见解析,数学期望为2;(ii)false;(2)false;分类讨论,答案见解析.
【详解】
(1)(i)因为false,所以控制系统中正常工作的元件个数false的可能取值为0,1,2,3;
因为每个元件的工作相互独立,且正常工作的概率均为false,
所以false,
所以false,
false
false,
false,
所以控制系统中正常工作的元件个数false的分布列为
false
0
1
2
3
false
false
false
false
false
控制系统中正常工作的元件个数false的数学期望为false;
(ii)由题意知:
false
false;
(2)升级改造后单位时间内产量的分布列为
产量
false
0
设备运行概率
false
false
所以升级改造后单位时间内产量的期望为false;
所以
产品类型
高端产品
一般产品
产量(单位:件)
false
false
利润(单位:元)
2
1
设备升级后单位时间内的利润为
false,即false;
因为控制系统中元件总数为奇数,若增加2个元件,则第一类:原系统中至少有false个元件正常工作,其概率为false;
第二类:原系统中恰好有false个元件正常工作,新增2个元件中至少有1个正常工作,其概率为
false;
第三类:原系统中有false个元件正常工作,新增2个元件全部正常工作,其概率为
false;
所以false
false,
即false,
所以当false时,false,false单调递增,
即增加元件个数设备正常工作的概率变大,
当false时,false,
即增加元件个数设备正常工作的概率没有变大,
又因为false,
所以当false时,设备可以通过增加控制系统中元件的个数来提高利润;
当false时,设备不可以通过增加控制系统中元件的个数来提高利润.
4.(1)false,false,false;(2)false;(3)分布列见解析,false.
【详解】
(1)由题意得:false,解得:false;false;则false,解得:false.
(2)日均步行数在false内的频率为:false,
日均步行数在false内的频率为false,
则false,解得:false.
false当false时,全校false的教职工能够得到奖励.
(3)由题意知:该校得到奖励的教职工在全校教职工中所占的比例为false,
false日均步行数不低于false千步的教职工在得到奖励的教职工所占的比例为false,false,
false,false,false,false,
false的分布列为:
false
false
false
false
false
false
false
false
false
false
数学期望false.
5.(1)false;(2)分布列见解析,1;(3)false.
【详解】
解:(1)因为false,
所以false.
(2)依题意,随机变量X的所有可能取值为0,1,2.
则false,false,
false.
所以随机变量X的分布列为
X
0
1
2
P
false
false
false
故X的数学期望false.
(3)设事件false{随机抽取一名职工,对工会工作服务“比较满意”}.
因为样本人数200人,其中男职工共有80人,
所以样本中女职工共有120人.
由频率分布直方图可知,
女职工对工会工作服务“比较满意”的人数共有:false人.
由频数分布表,可知男职工对工会工作“比较满意”的共有16人,
所以随机抽取一名职工,对工会工作“比较满意”的概率为false.
6.(1)分布列见解析,false;(2)答案见解析.
【详解】
(1)选全理(即化学+生物)或全文(即政治+地理)的概率为false, 即记false分的概率为false,因而记false分的概率为false,
易知false的可能取值为false、false、false、false,且false,false,false,false,
∴false的分布列为:
false
false
false
false
false
false
false
false
false
false
∴false;
(2)分情况进行讨论:
组合①:false人中选择①的有false人,其频率为false,预测全校false名学生选择①的人数为false,独立成一个班,剩下false人,
组合②:false人中选择②的有false人,其频率为false,预测全校false名学生选择②的人数为false,独立成八个50人的班,剩下false人,
组合③:false人中选择③的有false人,其频率为false,预测全校false名学生选择③的人数为false,独立成十个班,
组合④:false人中选择④的有false人,其频率为false,预测全校false名学生选择④的人数为false,独立成二个班,至少剩下false人,
组合⑤:false人中选择⑤的有false人,其频率为false,预测全校false名学生选择⑤的人数为false,独立成一个班,至少剩下false人,
组合⑥:false人中选择⑥的有false人,其频率为false,预测全校false名学生选择⑥的人数为false,独立成一个班,
①
⑤
②
④
化学+生物
化学+政治
生物+地理
生物+政治
false人
false人
false人
false人
减小混合班个数,把①⑤中独立班的人数调整为47到49人,剩下的学生组合成一个混合班,把②④剩下的学生组合成一个混合班(②组成的独立成八个班中每班减少false人).
