8.3 列联表与独立性检验 学案-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(wordl含答案)
文档属性
| 名称 | 8.3 列联表与独立性检验 学案-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(wordl含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 278.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-09 13:04:23 | ||
图片预览




文档简介
1201420011544300第八章 成对数据的统计分析
第八章 成对数据的统计分析
8.3列联表与独立性检验
8.3列联表与独立性检验
知识梳理
知识梳理
知识点1.分类变量与列联表
分类变量
为了方便,会使用一种________的随机变量,区别不同的现象或性质,这随机变量称为________变量.分类变量的取值可以用________表示.
列联表
(1).2×2列联表给出了________分类变量数据的交叉分类频数.
(2).定义一对分类变量X和Y,我们整理数据如下表所示:
X
Y
合计
Y=0
Y=1
X=0
a
b
a+b
X=1
c
d
c+d
合计
a+c
b+d
n=________
像这种形式的数据统计表称为2×2列联表.
3.两个分类变量之间关联关系的定性分析方法
(1)频率分析法:通过对________的分类变量的不同类别事件发生的频率大小进行分析分类变量之间是否有关联关系.通常通过列联表列出两个分类变量的频数表来进行分析.
(2)图形分析法:与表格相比,图形更能直观地反映两个分类变量间是否互相________,常用等高堆积条形图展示列联表数据的频率特征.
知识点2.独立性检验
1.定义:利用χ2的取值推断分类变量X和Y是否独立的方法称为χ2________检验,读作“卡方独立性检验”.简称独立性检验.
2.χ2=,其中n=a+b+c+d.
3.独立性检验解决实际问题的主要环节
(1)提出零假设H0:X和Y相互________,并给出在问题中的解释.
(2)根据抽样数据整理出2×2列联表,计算χ2的值,并与临界值xα比较.
(3)根据检验规则得出推断结论.
(4)在X和Y不独立的情况下,根据需要,通过比较________的频率,分析X和Y间的影响规律.
课后小练
课后小练
1.2021年2月25日举行的全国脱贫攻坚总结表彰大会上,国家电网共有23名(个)先进个人、先进集体获得表彰.其中,国网西藏电力有限公司农电工作部从习近平总书记手中接过了“全国脱贫攻坚楷模”奖牌.过去8年,在党中央坚强领导下,经过世界规模最大、力度最强的脱贫攻坚战,近1亿人摆脱绝对贫困.长期以来贫困地区的农产品面临“种得出卖不出”“酒香也怕巷子深”的困境.深谙互联网思维的国家电网人,搭平台、建渠道,以一款APP让众多贫困地区的产品销售易如反掌.2020年“6.18”期间,带货主播和直播运营两大岗位高达去年同期的11.6倍.针对这一市场现象,为了加强监管,相关管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出100次成功交易,并对其评价进行统计,对商品的好评率为0.6,对商品和服务都做出好评的交易为40次,对商品和服务部不满意的交易为5次.
(1)请完成关于商品和服务评价的false列联表,并判断能否在犯错误的概率不超过0.025的前提下,认为商品好与服务好评有关?
对服务好评
对服务不满意
合计
对商品好评
40
对商品不满意
5
合计
100
(2)从“对服务不满意”的评价中分层选出10个,再从这10个评价中随机选出6个,记其中“对商品不满意”的个数为false,求false的分布列及数学期望.
附:false,false.
false
0.15
0.10
0.05
0.025
0.010
0.005
0.001
false
2.072
2.706
3.841
5.024
6.635
7.879
10.828
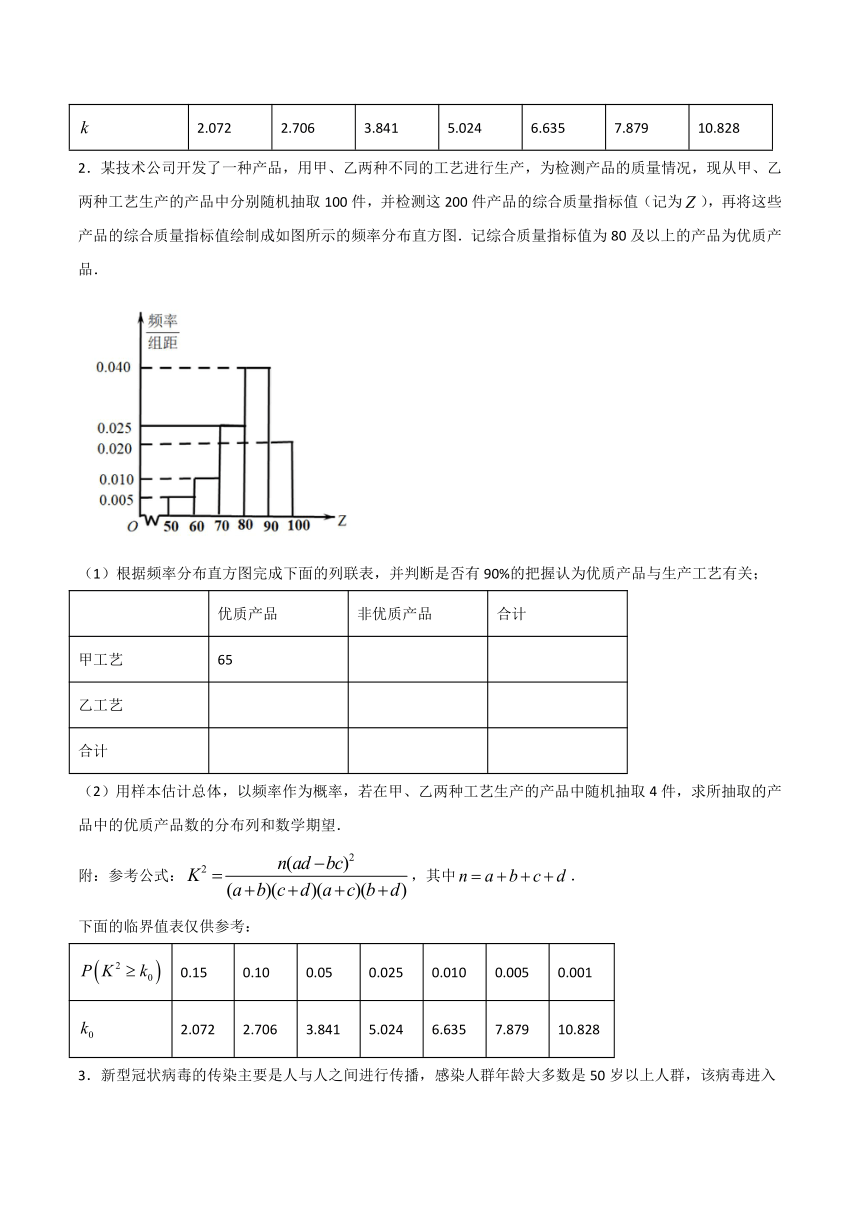
2.某技术公司开发了一种产品,用甲、乙两种不同的工艺进行生产,为检测产品的质量情况,现从甲、乙两种工艺生产的产品中分别随机抽取100件,并检测这200件产品的综合质量指标值(记为false),再将这些产品的综合质量指标值绘制成如图所示的频率分布直方图.记综合质量指标值为80及以上的产品为优质产品.
(1)根据频率分布直方图完成下面的列联表,并判断是否有90%的把握认为优质产品与生产工艺有关;
优质产品
非优质产品
合计
甲工艺
65
乙工艺
合计
(2)用样本估计总体,以频率作为概率,若在甲、乙两种工艺生产的产品中随机抽取4件,求所抽取的产品中的优质产品数的分布列和数学期望.
附:参考公式:false,其中false.
下面的临界值表仅供参考:
false
0.15
0.10
0.05
0.025
0.010
0.005
0.001
false
2.072
2.706
3.841
5.024
6.635
7.879
10.828
3.新型冠状病毒的传染主要是人与人之间进行传播,感染人群年龄大多数是50岁以上人群,该病毒进入人体后有潜伏期,潜伏期是指病原体侵入人体至最早出现临床症状的这段时间,潜伏期越长,感染到他人的可能性越高,现对400个病例的潜伏期(单位:天)进行调查,统计发现潜伏期平均数为false,方差为false,如果认为超过false天的潜伏期属于“长潜伏期”,按照年龄统计样本,50岁以上人数占false,长期潜伏人数占25%,其中50岁以上长期潜伏者有60人.
(1)请根据以上数据完成false列联表,并判断是否有false的把握认为“长期潜伏”与年龄有关;
false列联表,单位:人
50岁以下(含50岁)
50岁以上
总计
长期潜伏
非长期潜伏
总计
(2)假设潜伏期false服从正态分布false,其中false近似为样本平均数false,false近似为样本方差false,现在很多省市对入境旅客一律要求隔离14天,请结合false原则通过计算概率解释其合理性;
附:false
false
false
false
false
false
false
false
false
若false,false,false
4.某校的学习方法研究小组,设计了关于学习能力的问卷调查表,小组从高二年级学生中按性别(女生占55%)分层抽取n名同学进行调查,并把学生的学习能力由低到高按1,2,3,4,5五个基数进行赋分,形成如下条形图已知基数为2的学生人数占总调查人数的false.
(1)求n与a的值;
(2)若将某同学得分所在的基数false作为学习能力指标(基数false表示学习能力高,其他均为学习能力不高).在学习能力基数为5的学生中,男生与女生的比例为false,以本次抽取的n名同学为研究对象,完成下面的false列联表,并判断是否有90%的把握认为学习能力基数的高低与性别有关.
男生
女生
合计
学习能力基数高
学习能力基数不高
合计
(3)为了提高同学们的学习能力,该学习方法研究小组建议学校开设学习方法系列课程经过课程.学习之后,每位同学的学习能力T与学习能力基数false以及参加学习方法课程的次数k满足函数关系式false.如果学生A的学习能力基数为4,学生B的学习能力基数为2,则在A不参加学习方法课程的情况下,B至少需要参加多少次学习方法课程,其学习能力才能超过A?
参考数据及参考公式:false,false,
其中false.
false
0.15
0.10
0.05
0.01
false
2.072
2.706
3.841
6.635
5.目前我市逐步建立了以政府为主导以企业为主体,全社会共同推进的节能减排工作机制某企业响应号召,对现有设备进行改造,为了分析设备改造前后的效果,现从设备改造前后生产的大量产品中各抽取了200件产品作为样本,检测一项质量指标值,若该项质量指标值落在false内的产品视为合格品,否则为不合格品.如图是设备改造前的样本的频率分布直方图,如表是设备改造后的样本的频数分布表.
设备改造前样本的频率分布直方图:
设备改造后样本的频数分布表:
质量指示值
false
false
false
false
false
false
频数
4
36
96
28
32
4
(1)完成下面的false列联表,并判断是否有false的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
设备改造前
设备改造后
合计
合格品
不合格品
合计
(2)根据市场调查,设备改造后,每生产一件合格品企业可获利180元,一件不合格品亏损10元,用频率估计概率,则生产1000件产品企业大约能获利多少元?
附:
false
0.150
0.100
0.050
0.025
0.010
false
2.072
2.706
3.841
5.024
6.635
false
参考答案
1.(1)列联表见解析,能;(2)分布列见解析,false.
【详解】
(1)由题意可得关于商品和服务评价的false列联表如下:
对服务好评
对服务不满意
合计
对商品好评
40
20
60
对商品不满意
35
5
40
合计
75
25
100
false,
故能在犯错误的概率不超过0.025的前提下,认为商品好评与服务好评有关.
(2)由(1)得从“对服务不满意”的评价中分层选出的10个评价中,“对商品好评”的有8个,“对商品不满意”的有2个,故false的所有可能取值为0,1,2,
false,false,false,
false
0
1
2
false
false
false
false
所以false.
2.(1)答案见解析;没有;(2)分布列见解析;期望为false.
【详解】
(1)由频率分布直方图知,优质产品的频率为false,
则样本中,优质产品的件数为120件,列联表如下表所示:
优质产品
非优质产品
合计
甲工艺
65
35
100
乙工艺
55
45
100
合计
120
80
200
可得false.
∴没有90%的把握认为优质产品与生产工艺有关.
(2)由频率分布直方图得优质产品的频率为0.6,即概率为0.6,
设所抽取的产品为优质产品的件数为false,则false,
false;
false;
false;
false;
false.
其分布列为:
false
0
1
2
3
4
false
false
false
false
false
false
∴所抽取的产品为优质产品的数学期望false.
3.(1)列联表答案见解析,有false以上的把握认为“长期潜伏”与年龄有关;(2)答案见解析.
【详解】
(1)false列联表,单位:人
50岁以下(含50岁)
50岁以上
总计
长期潜伏
40
60
100
非长期潜伏
80
220
300
总计
120
280
400
false,
所以有false以上的把握认为“长期潜伏”与年龄有关.
(2)因为false,
所以潜伏期超过14天的概率很低,因此14天是合理的
4.(1)false ,false;(2)列联表见解析,没有把握;(3)17次.
【详解】
(1)false,所以false ,
false ;
(2)学习能力基数为5的学生中,男生与女生的比例为false,男生的6人,女生有14人,false列联表如表所示.
男生
女生
合计
学习能力基数高
6
14
20
学习能力基数不高
39
41
80
合计
45
55
100
false ,
所以没有90%的把握认为销售能力基数高不高与性别有关 ;
(3)学生A的学习能力false.学生B在参加了k次学习方法课程后,其学习能力false ,
由已知得false,即false,false ,
所以学生B至少需要参加17次学习方法课程,其学习能力指数才能超过学生A.
5.(1)填表见解析;有;(2)该企业大约能获利168800元.
【详解】
(1)设备改造前质量指标值不落在false内的产品有false,
因此设备改造前质量指标值落在false内的产品有false;
设备改造后质量指标值不落在false内的产品有false,
设备改造后质量指标值落在false内的产品有false,
根据以上的计算可得false列联表:
设备改造前
设备改造后
合计
合格品
172
192
364
不合格品
28
8
36
合计
200
200
400
将false列联表中的数据代入公式计算得:false,
false,
false有false的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
(2)用频率估计概率,1000件产品中大约有960件合格品,40件不合格品,
则获利约为false,
因此,该企业大约能获利168800元.
第八章 成对数据的统计分析
8.3列联表与独立性检验
8.3列联表与独立性检验
知识梳理
知识梳理
知识点1.分类变量与列联表
分类变量
为了方便,会使用一种________的随机变量,区别不同的现象或性质,这随机变量称为________变量.分类变量的取值可以用________表示.
列联表
(1).2×2列联表给出了________分类变量数据的交叉分类频数.
(2).定义一对分类变量X和Y,我们整理数据如下表所示:
X
Y
合计
Y=0
Y=1
X=0
a
b
a+b
X=1
c
d
c+d
合计
a+c
b+d
n=________
像这种形式的数据统计表称为2×2列联表.
3.两个分类变量之间关联关系的定性分析方法
(1)频率分析法:通过对________的分类变量的不同类别事件发生的频率大小进行分析分类变量之间是否有关联关系.通常通过列联表列出两个分类变量的频数表来进行分析.
(2)图形分析法:与表格相比,图形更能直观地反映两个分类变量间是否互相________,常用等高堆积条形图展示列联表数据的频率特征.
知识点2.独立性检验
1.定义:利用χ2的取值推断分类变量X和Y是否独立的方法称为χ2________检验,读作“卡方独立性检验”.简称独立性检验.
2.χ2=,其中n=a+b+c+d.
3.独立性检验解决实际问题的主要环节
(1)提出零假设H0:X和Y相互________,并给出在问题中的解释.
(2)根据抽样数据整理出2×2列联表,计算χ2的值,并与临界值xα比较.
(3)根据检验规则得出推断结论.
(4)在X和Y不独立的情况下,根据需要,通过比较________的频率,分析X和Y间的影响规律.
课后小练
课后小练
1.2021年2月25日举行的全国脱贫攻坚总结表彰大会上,国家电网共有23名(个)先进个人、先进集体获得表彰.其中,国网西藏电力有限公司农电工作部从习近平总书记手中接过了“全国脱贫攻坚楷模”奖牌.过去8年,在党中央坚强领导下,经过世界规模最大、力度最强的脱贫攻坚战,近1亿人摆脱绝对贫困.长期以来贫困地区的农产品面临“种得出卖不出”“酒香也怕巷子深”的困境.深谙互联网思维的国家电网人,搭平台、建渠道,以一款APP让众多贫困地区的产品销售易如反掌.2020年“6.18”期间,带货主播和直播运营两大岗位高达去年同期的11.6倍.针对这一市场现象,为了加强监管,相关管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出100次成功交易,并对其评价进行统计,对商品的好评率为0.6,对商品和服务都做出好评的交易为40次,对商品和服务部不满意的交易为5次.
(1)请完成关于商品和服务评价的false列联表,并判断能否在犯错误的概率不超过0.025的前提下,认为商品好与服务好评有关?
对服务好评
对服务不满意
合计
对商品好评
40
对商品不满意
5
合计
100
(2)从“对服务不满意”的评价中分层选出10个,再从这10个评价中随机选出6个,记其中“对商品不满意”的个数为false,求false的分布列及数学期望.
附:false,false.
false
0.15
0.10
0.05
0.025
0.010
0.005
0.001
false
2.072
2.706
3.841
5.024
6.635
7.879
10.828
2.某技术公司开发了一种产品,用甲、乙两种不同的工艺进行生产,为检测产品的质量情况,现从甲、乙两种工艺生产的产品中分别随机抽取100件,并检测这200件产品的综合质量指标值(记为false),再将这些产品的综合质量指标值绘制成如图所示的频率分布直方图.记综合质量指标值为80及以上的产品为优质产品.
(1)根据频率分布直方图完成下面的列联表,并判断是否有90%的把握认为优质产品与生产工艺有关;
优质产品
非优质产品
合计
甲工艺
65
乙工艺
合计
(2)用样本估计总体,以频率作为概率,若在甲、乙两种工艺生产的产品中随机抽取4件,求所抽取的产品中的优质产品数的分布列和数学期望.
附:参考公式:false,其中false.
下面的临界值表仅供参考:
false
0.15
0.10
0.05
0.025
0.010
0.005
0.001
false
2.072
2.706
3.841
5.024
6.635
7.879
10.828
3.新型冠状病毒的传染主要是人与人之间进行传播,感染人群年龄大多数是50岁以上人群,该病毒进入人体后有潜伏期,潜伏期是指病原体侵入人体至最早出现临床症状的这段时间,潜伏期越长,感染到他人的可能性越高,现对400个病例的潜伏期(单位:天)进行调查,统计发现潜伏期平均数为false,方差为false,如果认为超过false天的潜伏期属于“长潜伏期”,按照年龄统计样本,50岁以上人数占false,长期潜伏人数占25%,其中50岁以上长期潜伏者有60人.
(1)请根据以上数据完成false列联表,并判断是否有false的把握认为“长期潜伏”与年龄有关;
false列联表,单位:人
50岁以下(含50岁)
50岁以上
总计
长期潜伏
非长期潜伏
总计
(2)假设潜伏期false服从正态分布false,其中false近似为样本平均数false,false近似为样本方差false,现在很多省市对入境旅客一律要求隔离14天,请结合false原则通过计算概率解释其合理性;
附:false
false
false
false
false
false
false
false
false
若false,false,false
4.某校的学习方法研究小组,设计了关于学习能力的问卷调查表,小组从高二年级学生中按性别(女生占55%)分层抽取n名同学进行调查,并把学生的学习能力由低到高按1,2,3,4,5五个基数进行赋分,形成如下条形图已知基数为2的学生人数占总调查人数的false.
(1)求n与a的值;
(2)若将某同学得分所在的基数false作为学习能力指标(基数false表示学习能力高,其他均为学习能力不高).在学习能力基数为5的学生中,男生与女生的比例为false,以本次抽取的n名同学为研究对象,完成下面的false列联表,并判断是否有90%的把握认为学习能力基数的高低与性别有关.
男生
女生
合计
学习能力基数高
学习能力基数不高
合计
(3)为了提高同学们的学习能力,该学习方法研究小组建议学校开设学习方法系列课程经过课程.学习之后,每位同学的学习能力T与学习能力基数false以及参加学习方法课程的次数k满足函数关系式false.如果学生A的学习能力基数为4,学生B的学习能力基数为2,则在A不参加学习方法课程的情况下,B至少需要参加多少次学习方法课程,其学习能力才能超过A?
参考数据及参考公式:false,false,
其中false.
false
0.15
0.10
0.05
0.01
false
2.072
2.706
3.841
6.635
5.目前我市逐步建立了以政府为主导以企业为主体,全社会共同推进的节能减排工作机制某企业响应号召,对现有设备进行改造,为了分析设备改造前后的效果,现从设备改造前后生产的大量产品中各抽取了200件产品作为样本,检测一项质量指标值,若该项质量指标值落在false内的产品视为合格品,否则为不合格品.如图是设备改造前的样本的频率分布直方图,如表是设备改造后的样本的频数分布表.
设备改造前样本的频率分布直方图:
设备改造后样本的频数分布表:
质量指示值
false
false
false
false
false
false
频数
4
36
96
28
32
4
(1)完成下面的false列联表,并判断是否有false的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
设备改造前
设备改造后
合计
合格品
不合格品
合计
(2)根据市场调查,设备改造后,每生产一件合格品企业可获利180元,一件不合格品亏损10元,用频率估计概率,则生产1000件产品企业大约能获利多少元?
附:
false
0.150
0.100
0.050
0.025
0.010
false
2.072
2.706
3.841
5.024
6.635
false
参考答案
1.(1)列联表见解析,能;(2)分布列见解析,false.
【详解】
(1)由题意可得关于商品和服务评价的false列联表如下:
对服务好评
对服务不满意
合计
对商品好评
40
20
60
对商品不满意
35
5
40
合计
75
25
100
false,
故能在犯错误的概率不超过0.025的前提下,认为商品好评与服务好评有关.
(2)由(1)得从“对服务不满意”的评价中分层选出的10个评价中,“对商品好评”的有8个,“对商品不满意”的有2个,故false的所有可能取值为0,1,2,
false,false,false,
false
0
1
2
false
false
false
false
所以false.
2.(1)答案见解析;没有;(2)分布列见解析;期望为false.
【详解】
(1)由频率分布直方图知,优质产品的频率为false,
则样本中,优质产品的件数为120件,列联表如下表所示:
优质产品
非优质产品
合计
甲工艺
65
35
100
乙工艺
55
45
100
合计
120
80
200
可得false.
∴没有90%的把握认为优质产品与生产工艺有关.
(2)由频率分布直方图得优质产品的频率为0.6,即概率为0.6,
设所抽取的产品为优质产品的件数为false,则false,
false;
false;
false;
false;
false.
其分布列为:
false
0
1
2
3
4
false
false
false
false
false
false
∴所抽取的产品为优质产品的数学期望false.
3.(1)列联表答案见解析,有false以上的把握认为“长期潜伏”与年龄有关;(2)答案见解析.
【详解】
(1)false列联表,单位:人
50岁以下(含50岁)
50岁以上
总计
长期潜伏
40
60
100
非长期潜伏
80
220
300
总计
120
280
400
false,
所以有false以上的把握认为“长期潜伏”与年龄有关.
(2)因为false,
所以潜伏期超过14天的概率很低,因此14天是合理的
4.(1)false ,false;(2)列联表见解析,没有把握;(3)17次.
【详解】
(1)false,所以false ,
false ;
(2)学习能力基数为5的学生中,男生与女生的比例为false,男生的6人,女生有14人,false列联表如表所示.
男生
女生
合计
学习能力基数高
6
14
20
学习能力基数不高
39
41
80
合计
45
55
100
false ,
所以没有90%的把握认为销售能力基数高不高与性别有关 ;
(3)学生A的学习能力false.学生B在参加了k次学习方法课程后,其学习能力false ,
由已知得false,即false,false ,
所以学生B至少需要参加17次学习方法课程,其学习能力指数才能超过学生A.
5.(1)填表见解析;有;(2)该企业大约能获利168800元.
【详解】
(1)设备改造前质量指标值不落在false内的产品有false,
因此设备改造前质量指标值落在false内的产品有false;
设备改造后质量指标值不落在false内的产品有false,
设备改造后质量指标值落在false内的产品有false,
根据以上的计算可得false列联表:
设备改造前
设备改造后
合计
合格品
172
192
364
不合格品
28
8
36
合计
200
200
400
将false列联表中的数据代入公式计算得:false,
false,
false有false的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
(2)用频率估计概率,1000件产品中大约有960件合格品,40件不合格品,
则获利约为false,
因此,该企业大约能获利168800元.
