七年级数学勾股定理
图片预览




文档简介
(共12张PPT)
勾股定理
——直角三角行三边之间的关系
1.回顾直角三角形有哪些特性?
2.直角三角形三边之间有怎样的数量关系?
3.请同学们拿出三角尺测量它的三边长并计算两条直角边的平方和、斜边长的平方
比较两条直角边的平方和、斜边长的平方的大小
猜想它们的关系
Q
P
Q
P
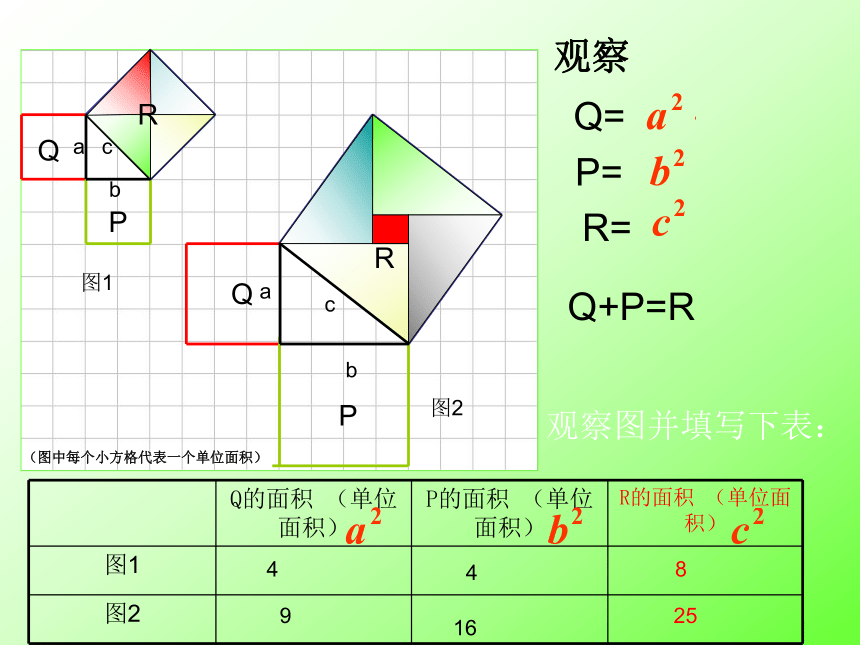
观察图并填写下表:
Q的面积 (单位面积) P的面积 (单位面积) R的面积 (单位面积)
图1
图2
观察
图1
图2
4
4
8
16
9
25
(图中每个小方格代表一个单位面积)
a
b
c
a
c
b
R
R
Q=
P=
R=
Q+P=R
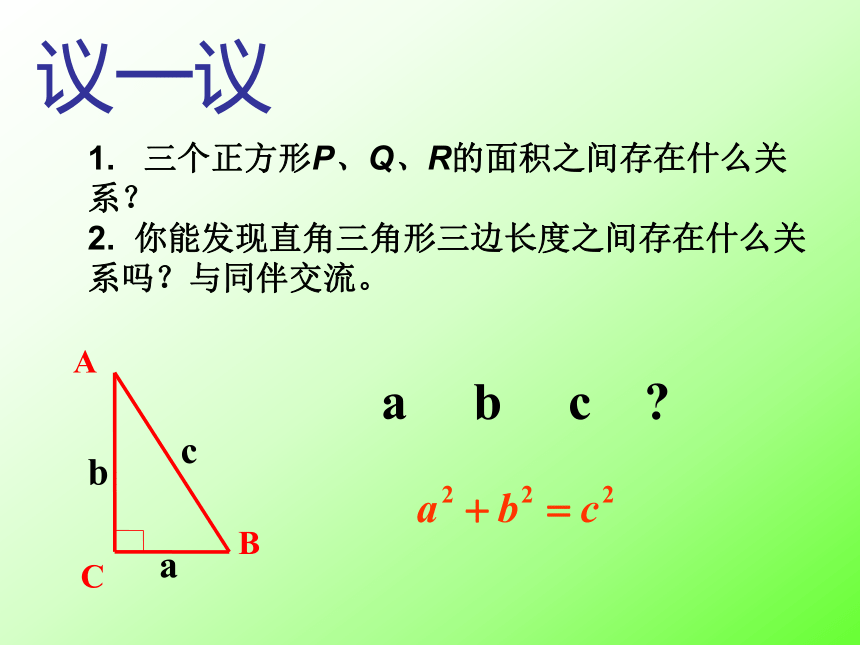
1. 三个正方形P、Q、R的面积之间存在什么关系?
2. 你能发现直角三角形三边长度之间存在什么关系吗?与同伴交流。
议一议
A
B
C
a
c
b
a b c
动动手
分别以5厘米、12厘米为直角三角形的直角边做出一个直角三角形,并测量斜边的长度.
前面得到的规律对这个三角形还成立吗?
2
3
4
5
6
7
8
9
10
11
12
13
14
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
0
1
5
12
13
勾股定理
如果直角三角形两直角边分别为a,b,斜边为c,那么
即直角三角形两直角边的平方和等于斜边的平方.
A
B
C
a
c
b
C=
a=
b=
一直角边 另一直角边 斜边
3 4
5 13
24 25
8 15
一直角边 另一直角边 斜边
3 4 5
6 8
9 12
12 16
3n 4n
5
17
在直角三角形中
凡是可以构成一个直角三角形三边的一组正整数,称之为 勾股数。
15
20
5n
10
如果一个直角三角形三边同时扩大n倍,那么这个三角形是 三角形
直角
12
7
实例
如图14.1.4,将长为5.41米的梯子AC斜靠在墙上,BC长为2.16米,
求梯子上端A到墙的底边的垂直距离AB.(精确到0.01米)
如图,在Rt△ABC中,BC=2.16米 AC=5.41米,
解:
根据勾股定理可得
AB=
答: 梯子上端A到墙的底边的垂直距离 AB 约为4.96米.
≈4.9(米).
做一做
32
60
A
225
B
81
1. 求下列图中字母所代表的正方形的面积
=92
=144
2. 在直角三角形中,其中两边为3和4,则第三边 是( )
A. 5 B.7 C. D.5或
7
7
3
3
4
4
7
5
D
3. 在一直角三角形中,两直角边分别为3和4,则斜边上的高是( )
A. 5 B. 7 C. 2.4 D. 12
3
4
5
h
A
B
C
C
作业:
1、阅读课本P55~56;勾股定理史话
2、必做题目:课本P55,习题14.1,第2、 3题。
再见
勾股定理
——直角三角行三边之间的关系
1.回顾直角三角形有哪些特性?
2.直角三角形三边之间有怎样的数量关系?
3.请同学们拿出三角尺测量它的三边长并计算两条直角边的平方和、斜边长的平方
比较两条直角边的平方和、斜边长的平方的大小
猜想它们的关系
Q
P
Q
P
观察图并填写下表:
Q的面积 (单位面积) P的面积 (单位面积) R的面积 (单位面积)
图1
图2
观察
图1
图2
4
4
8
16
9
25
(图中每个小方格代表一个单位面积)
a
b
c
a
c
b
R
R
Q=
P=
R=
Q+P=R
1. 三个正方形P、Q、R的面积之间存在什么关系?
2. 你能发现直角三角形三边长度之间存在什么关系吗?与同伴交流。
议一议
A
B
C
a
c
b
a b c
动动手
分别以5厘米、12厘米为直角三角形的直角边做出一个直角三角形,并测量斜边的长度.
前面得到的规律对这个三角形还成立吗?
2
3
4
5
6
7
8
9
10
11
12
13
14
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
0
1
5
12
13
勾股定理
如果直角三角形两直角边分别为a,b,斜边为c,那么
即直角三角形两直角边的平方和等于斜边的平方.
A
B
C
a
c
b
C=
a=
b=
一直角边 另一直角边 斜边
3 4
5 13
24 25
8 15
一直角边 另一直角边 斜边
3 4 5
6 8
9 12
12 16
3n 4n
5
17
在直角三角形中
凡是可以构成一个直角三角形三边的一组正整数,称之为 勾股数。
15
20
5n
10
如果一个直角三角形三边同时扩大n倍,那么这个三角形是 三角形
直角
12
7
实例
如图14.1.4,将长为5.41米的梯子AC斜靠在墙上,BC长为2.16米,
求梯子上端A到墙的底边的垂直距离AB.(精确到0.01米)
如图,在Rt△ABC中,BC=2.16米 AC=5.41米,
解:
根据勾股定理可得
AB=
答: 梯子上端A到墙的底边的垂直距离 AB 约为4.96米.
≈4.9(米).
做一做
32
60
A
225
B
81
1. 求下列图中字母所代表的正方形的面积
=92
=144
2. 在直角三角形中,其中两边为3和4,则第三边 是( )
A. 5 B.7 C. D.5或
7
7
3
3
4
4
7
5
D
3. 在一直角三角形中,两直角边分别为3和4,则斜边上的高是( )
A. 5 B. 7 C. 2.4 D. 12
3
4
5
h
A
B
C
C
作业:
1、阅读课本P55~56;勾股定理史话
2、必做题目:课本P55,习题14.1,第2、 3题。
再见
