人教版八年级数学上册 11.2.2 三角形的外角2 教案
文档属性
| 名称 | 人教版八年级数学上册 11.2.2 三角形的外角2 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 47.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 00:21:00 | ||
图片预览

文档简介
学科
数学
年级/册
八年级上册
教材版本
人教版
课题名称
第十一章
三角形外角及性质
教学目标
1.理解并掌握三角形的外角的概念和性质.
2.利用三角形的外角的性质解决燕尾模型角度问题
重难点分析
重点分析
1.理解并掌握三角形的外角的概念和性质.
2.利用三角形的外角的性质解决燕尾模型角度问题
难点分析
培养类比建模思想,作辅助线知识的应用能力,渗透逻辑推理的训练.
教学方法
让学生应用三角形外角的性质解决学习和生活中的有关问题,发散思维,提高空间想象能力。
逐步养成数学推理的习惯和建模思想的培养。
教学环节
教学过程
导入
回顾旧知识:
(1)什么叫三角形的外角:?
三角形的(
一边)与(另一边
)的延长线组成的角,叫做三角形的外角.
如∠ACD是△ABC的一个外角
画一个△ABC
,你能画出它的所有外角来吗?请动手试一试.同时想一想△ABC的外角共有几个呢?
归纳:1.每一个三角形都有6个外角.每一个顶点相对应的外角都有2个.每个外角与相邻的内角是邻补角.
推论2:三角形的一个外角等于与它不相邻的两个内角的和。
推论3:三角形的一个外角大于与它不相邻的任何一个内角。
知识讲解
(难点突破)
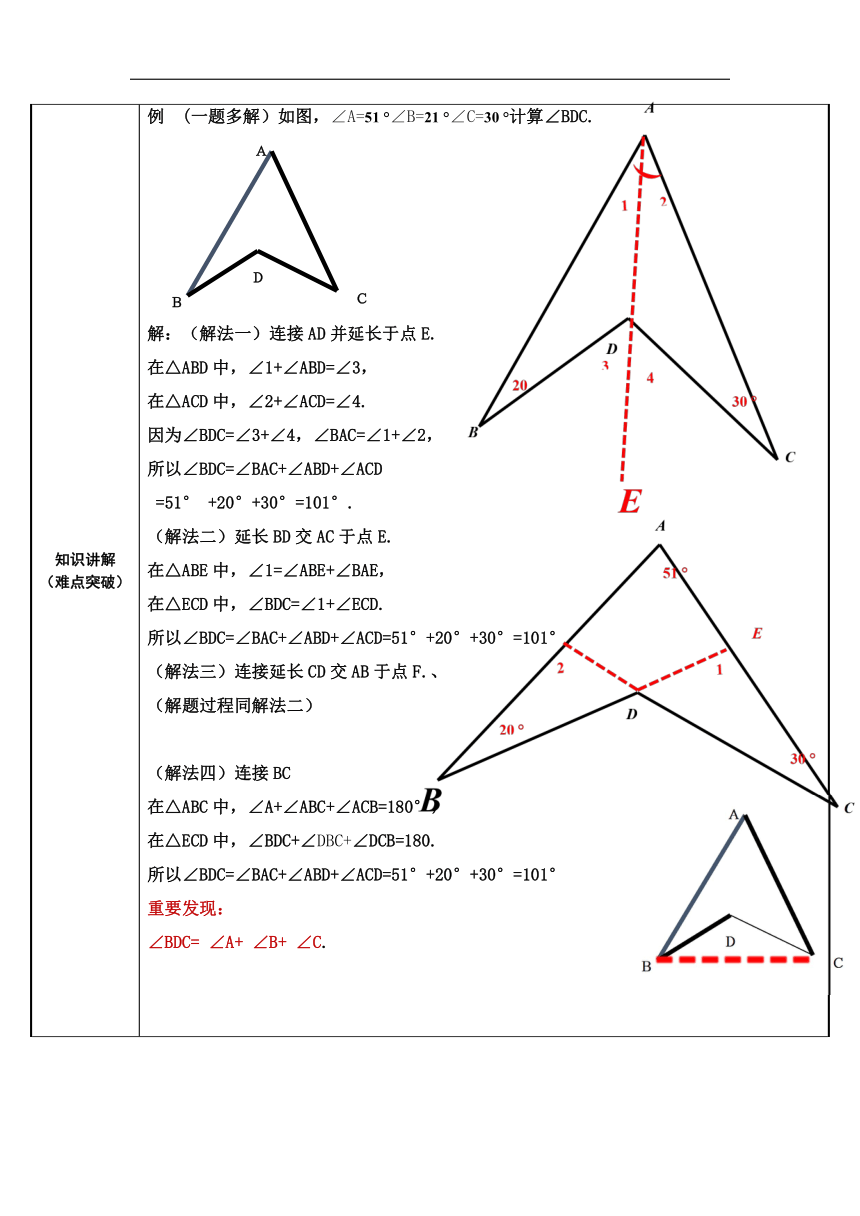
例
(一题多解)如图,∠A=51
°∠B=21
°∠C=30
°计算∠BDC.
解:(解法一)连接AD并延长于点E.
在△ABD中,∠1+∠ABD=∠3,
在△ACD中,∠2+∠ACD=∠4.
因为∠BDC=∠3+∠4,∠BAC=∠1+∠2,
所以∠BDC=∠BAC+∠ABD+∠ACD
=51°
+20°+30°=101°.
(解法二)延长BD交AC于点E.
在△ABE中,∠1=∠ABE+∠BAE,
在△ECD中,∠BDC=∠1+∠ECD.
所以∠BDC=∠BAC+∠ABD+∠ACD=51°+20°+30°=101°.
(解法三)连接延长CD交AB于点F.、
(解题过程同解法二)
(解法四)连接BC
在△ABC中,∠A+∠ABC+∠ACB=180°,
在△ECD中,∠BDC+∠DBC+∠DCB=180.
所以∠BDC=∠BAC+∠ABD+∠ACD=51°+20°+30°=101°
重要发现:
∠BDC=
∠A+
∠B+
∠C.
课堂练习
(难点巩固)
1.如图,求∠A+
∠B+
∠C+
∠D+
∠E的度数
解:因为∠A+
∠C=
∠EFG∠B+
∠D=
∠EGF
∠EGF
+
∠EFG
+
∠E
=
180°
所以∠A+
∠B+
∠C+
∠D+
∠E=
180°
2.已知:如下图,在△ABC中,
∠1是它的一个
外角,
E为边AC上一点,延长BC到D,连接DE.
求证:
∠1>∠2.
证明:∵
∠1是△ABC的一个外角(已知),
∴
∠1>∠3
(
三角形的一个外角大于任何
一个和它不相邻的内角
).
∵∠3是△CDE的一个外角
(外角定义).
∴∠3>∠2
(三角形的一个外角大于任何一个和它不相邻的内角).
∴
∠1>∠2(不等式的性质).
3.如图,求∠A+∠B+∠C+∠D+∠E+∠F=___
解:∵∠1是△ABN的外角
∴∠1=∠A+∠B
∵∠2是△CDP的外角
∴∠2=∠C+∠D
∵∠3是△MEF的外角
∴∠3=∠F+∠E
又∵∠1,∠2,∠3是△PMN的外角
∴∠1+∠2+∠3=360°
∴∠A+∠B+∠C+∠D+∠E+∠F=360°
小结
三、课堂小结:
[归纳总结]
外角可以把不在同一三角形中的几个角联系起来。解决问题的关键:
一是确定角的“身份”——内角还是外角;
二是添加辅助线构造三角形的外角。
数学
年级/册
八年级上册
教材版本
人教版
课题名称
第十一章
三角形外角及性质
教学目标
1.理解并掌握三角形的外角的概念和性质.
2.利用三角形的外角的性质解决燕尾模型角度问题
重难点分析
重点分析
1.理解并掌握三角形的外角的概念和性质.
2.利用三角形的外角的性质解决燕尾模型角度问题
难点分析
培养类比建模思想,作辅助线知识的应用能力,渗透逻辑推理的训练.
教学方法
让学生应用三角形外角的性质解决学习和生活中的有关问题,发散思维,提高空间想象能力。
逐步养成数学推理的习惯和建模思想的培养。
教学环节
教学过程
导入
回顾旧知识:
(1)什么叫三角形的外角:?
三角形的(
一边)与(另一边
)的延长线组成的角,叫做三角形的外角.
如∠ACD是△ABC的一个外角
画一个△ABC
,你能画出它的所有外角来吗?请动手试一试.同时想一想△ABC的外角共有几个呢?
归纳:1.每一个三角形都有6个外角.每一个顶点相对应的外角都有2个.每个外角与相邻的内角是邻补角.
推论2:三角形的一个外角等于与它不相邻的两个内角的和。
推论3:三角形的一个外角大于与它不相邻的任何一个内角。
知识讲解
(难点突破)
例
(一题多解)如图,∠A=51
°∠B=21
°∠C=30
°计算∠BDC.
解:(解法一)连接AD并延长于点E.
在△ABD中,∠1+∠ABD=∠3,
在△ACD中,∠2+∠ACD=∠4.
因为∠BDC=∠3+∠4,∠BAC=∠1+∠2,
所以∠BDC=∠BAC+∠ABD+∠ACD
=51°
+20°+30°=101°.
(解法二)延长BD交AC于点E.
在△ABE中,∠1=∠ABE+∠BAE,
在△ECD中,∠BDC=∠1+∠ECD.
所以∠BDC=∠BAC+∠ABD+∠ACD=51°+20°+30°=101°.
(解法三)连接延长CD交AB于点F.、
(解题过程同解法二)
(解法四)连接BC
在△ABC中,∠A+∠ABC+∠ACB=180°,
在△ECD中,∠BDC+∠DBC+∠DCB=180.
所以∠BDC=∠BAC+∠ABD+∠ACD=51°+20°+30°=101°
重要发现:
∠BDC=
∠A+
∠B+
∠C.
课堂练习
(难点巩固)
1.如图,求∠A+
∠B+
∠C+
∠D+
∠E的度数
解:因为∠A+
∠C=
∠EFG∠B+
∠D=
∠EGF
∠EGF
+
∠EFG
+
∠E
=
180°
所以∠A+
∠B+
∠C+
∠D+
∠E=
180°
2.已知:如下图,在△ABC中,
∠1是它的一个
外角,
E为边AC上一点,延长BC到D,连接DE.
求证:
∠1>∠2.
证明:∵
∠1是△ABC的一个外角(已知),
∴
∠1>∠3
(
三角形的一个外角大于任何
一个和它不相邻的内角
).
∵∠3是△CDE的一个外角
(外角定义).
∴∠3>∠2
(三角形的一个外角大于任何一个和它不相邻的内角).
∴
∠1>∠2(不等式的性质).
3.如图,求∠A+∠B+∠C+∠D+∠E+∠F=___
解:∵∠1是△ABN的外角
∴∠1=∠A+∠B
∵∠2是△CDP的外角
∴∠2=∠C+∠D
∵∠3是△MEF的外角
∴∠3=∠F+∠E
又∵∠1,∠2,∠3是△PMN的外角
∴∠1+∠2+∠3=360°
∴∠A+∠B+∠C+∠D+∠E+∠F=360°
小结
三、课堂小结:
[归纳总结]
外角可以把不在同一三角形中的几个角联系起来。解决问题的关键:
一是确定角的“身份”——内角还是外角;
二是添加辅助线构造三角形的外角。
