2.7二次根式 综合应用专题突破训练 2021-2022学年北师大版八年级数学上册(Word版 含答案)
文档属性
| 名称 | 2.7二次根式 综合应用专题突破训练 2021-2022学年北师大版八年级数学上册(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 319.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 00:00:00 | ||
图片预览




文档简介
2021-2022学年北师大版八年级数学上册《2.7二次根式》综合应用专题突破训练(附答案)
一.选择题(共8小题)
1.如图,从一个大正方形中可以裁去面积为8cm2和32cm2的两个小正方形,则大正方形的边长为( )
A. B. C. D.
2.已知两条线段的长分别为和,当第三条线段的长取何值时,这三条线段能围成一个直角三角形( )
A.2 B.4 C.2或4 D.
3.在数学课上,老师将一长方形纸片的长增加,宽增加,就成为了一个面积为192cm2的正方形,则原长方形纸片的面积为( )
A.18cm2 B.20cm2 C.36cm2 D.48cm2
4.如图,已知阴影部分是一个正方形,AB=4,∠B=45°,此正方形的面积( )
A.16 B.8 C.4 D.2
5.已知△ABC的两边的长分别为2,5,则△ABC的周长不可能是( )
A.10 B.11 C.12 D.13
6.能与cm和cm的线段组成直角三角形的第三条线段的长是( )cm
A. B.1 C. D.或1
7.如图,在数学课上,老师用5个完全相同的小长方形在无重叠的情况下拼成了一个大长方形,已知小长方形的长为、宽为,下列是四位同学对该大长方形的判断,其中不正确的是( )
A.大长方形的长为6 B.大长方形的宽为5
C.大长方形的周长为11 D.大长方形的面积为90
8.△ABC的两边长分别为2和2,第三边上的高等于,则△ABC的面积是( )
A. B.2 C.或2 D.不能确定
二.填空题(共8小题)
9.如图,将长方形分成四个区域,其中A、B两正方形区域的面积分别是1和7,则剩余区域的面积是 .
10.一个直角三角形的两直角边长分别为cm和cm,则这个直角三角形的面积是 cm2.
11.如图,两个相邻的正方形ABCD和CEFG,其中B,C,E在同一条直线上,点D在CG上,它们的面积分别为27平方米和48平方米,则BE的长为 米.
12.已知△ABC中,AB=2AC,若AB边上的高为,△ABC的面积为2,则BC边的长为 .
13.如图,大、小两个正方形连在一起,大正方形的边长为10,小正方形的边长为6,则阴影部分的面积为 .
14.如图,在矩形ABCD中,不重叠地放上两张面积分别是5cm2和3cm2的正方形纸片BCHE和AEFG.矩形ABCD没被这两个正方形盖住的面积是 .
15.如图,D是等边三角形ABC中AC延长线上一点,连接BD,E是AB上一点,且DE=DB,若AD+AE=5,BE=,则BC= .
16.△ABC中,∠ACB=90°,∠A、∠B、∠C所对的边分别为a、b、c,已知它的周长为6+且c=.
(1)比较大小6 ;(2)△ABC的面积等于 .
三.解答题(共6小题)
17.一个矩形的长a=+,宽b=﹣.
(1)该矩形的面积= ,周长= ;
(2)求a2+b2+ab的值.
18.我国宋代的数学家秦九韶发现:若一个三角形的三边长分别为a,b,c,则这个三角形的面积为s=,其中p=(a+b+c).
如图1,在△ABC中,已知AB=9,AC=8,BC=7.
(1)求△ABC的面积;
(2)如图2,AD,BE为△ABC的两条角平分线,它们的交点为点I,求I到边BC的距离.
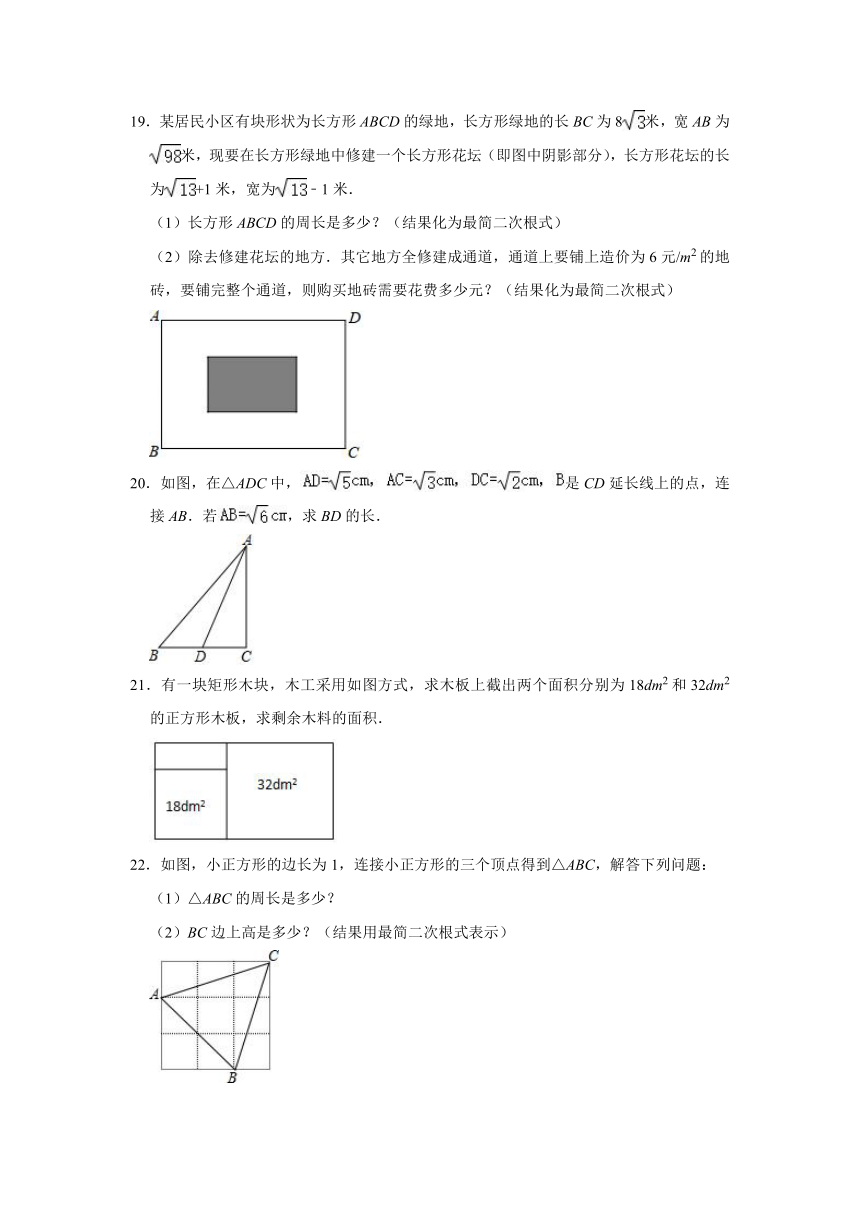
19.某居民小区有块形状为长方形ABCD的绿地,长方形绿地的长BC为8米,宽AB为米,现要在长方形绿地中修建一个长方形花坛(即图中阴影部分),长方形花坛的长为+1米,宽为﹣1米.
(1)长方形ABCD的周长是多少?(结果化为最简二次根式)
(2)除去修建花坛的地方.其它地方全修建成通道,通道上要铺上造价为6元/m2的地砖,要铺完整个通道,则购买地砖需要花费多少元?(结果化为最简二次根式)
20.如图,在△ADC中,是CD延长线上的点,连接AB.若,求BD的长.
21.有一块矩形木块,木工采用如图方式,求木板上截出两个面积分别为18dm2和32dm2的正方形木板,求剩余木料的面积.
22.如图,小正方形的边长为1,连接小正方形的三个顶点得到△ABC,解答下列问题:
(1)△ABC的周长是多少?
(2)BC边上高是多少?(结果用最简二次根式表示)
参考答案
一.选择题(共8小题)
1.解:从一个大正方形中裁去面积为 8cm2和 32cm2的两个小正方形,
则大正方形的边长是+=2+4=6.
故选:C.
2.解:设直角三角形的第三边为x,
当为斜边时,
由勾股定理可知:x2+6=10,
∴x=2,
当,为直角边时,
∴由勾股定理可知:6+10=x2,
∴x=4,
故选:C.
3.解:∵一个面积为192cm2的正方形纸片,边长为:8cm,
∴原矩形的长为:8﹣2=6(cm),宽为:8﹣7=(cm),
∴则原长方形纸片的面积为:(cm2).
故选:A.
4.解:∵AB=4,∠B=45°,
∴AC=AB?sin∠B=4×=2,
∴此正方形的面积为2×2=8.
故选:B.
5.解:设三角形的另一边长为x,
根据三角形三边关系可知:x<2+5,即x<7,
x>5﹣2,即x>3,
则3<x<7,
其周长L要满足:3+2+5<L<2+5+7,即10<L<14.
故选:D.
6.解:①是直角边时,第三边==cm,
②是斜边时,第三边==1cm,
所以,第三条线段的长是cm或1cm.
故选:D.
7.解:∵小长方形的长为=3、宽为=2,
∴大长方形的长为:,大长方形的宽为:,
大长方形的周长是:,大长方形的面积为:,
故选项C错误,选项A、B、D正确;
故选:C.
8.解:如图1,
根据题意,AB=2、AC=2,AD=,
∴BD==1,CD==3,
则S△ABC=×(1+3)×=2;
如图2,
S△ABC=×(3﹣1)×=,
故选:C.
二.填空题(共8小题)
9.解:∵A,B两正方形区域的面积分别是1和7,
∴A,B两正方形边长分别是1和,
故剩余区域的面积是:
(+1)﹣7﹣1
=7+﹣8
=﹣1.
故答案为:﹣1.
10.解:这个直角三角形的面积=cm2,
故答案为:2
11.∵正方形ABCD的面积为27,
∴BC=.
∵正方形CEFG的面积为48,
∴CE=.
∴BE=BC+CE=.
故答案为:.
12.解:AB=2×2÷=4,
则AC=AB=2,
在Rt△ADC中,AD===1
如图1,BD=AB﹣AD=4﹣1=3,
在Rt△CDB中,BC===2;
如图2,BD=AB+AD=4+1=5,
在Rt△CDB中,BC===2.
则BC边的长为2或2.
故答案为:2或2.
13.解:由图形可得,阴影部分的面积为:×10×10=50.
故答案为:50.
14.解:∵两张正方形纸片的面积分别为5cm2和3cm2,
∴它们的边长分别为cm和cm,
∴AB=(+)cm,BC=cm,
∴矩形ABCD没被这两个正方形盖住的面积是=﹣5﹣3=(﹣3)cm2,
故答案为:(﹣3)cm2.
15.解:过D作DF⊥AB于F,交BC于G,
∵DE=DB,
∴EF=BF=,
设AE=x,
∴AD=5﹣x,AF=AE+EF=x+,
∵△ABC是等边三角形,
∴∠A=60°,
∴∠ADF=30°,
∴AD=2AF,
即5﹣x=2(x+),
∴x=,
∴BC=AB=+=,
故答案为:.
16.解:(1)∵6=,
∴6>;
(2)∵∠ACB=90°,∠A、∠B、∠C所对的边分别为a、b、c,
它的周长为6+且c=,
∴a+b=6,a2+b2=c2=26,
∴(a+b)2=36,
∴a2+b2+2ab=36,
∴2ab=10,
∴ab=2.5.
故答案为:>,2.5.
三.解答题(共6小题)
17.解:(1)矩形的面积=ab==6﹣5=1;
周长=2(a+b)==4.
故答案为:1;.
(2)由(1)得:a+b=2,ab=1,
原式=(a+b)2﹣ab
=
=23.
18.解:(1)由题意得:p===12,
∴S△ABC===12;
(2)连接IC,过点I分别作AB、BC、AC边的垂线交AB、BC、AC于点M、Q、N,
由角平分线的性质定理可知:IM=IQ=IN,
观察图形易知:S△ABC=S△ABI+S△BCI+S△ACI===12,
∴=12,
解得:IQ=,
故I到边BC的距离为:.
19.解:(1)长方形ABCD的周长=2×()=2(8+7)=16+14(米),
答:长方形ABCD的周长是16+14(米),
(2)通道的面积=
=56﹣(13﹣1)
=56(平方米),
购买地砖需要花费=6×(56)=336﹣72(元).
答:购买地砖需要花费336﹣72元;
20.解:在,
∵AC2+DC2=3+5=AD2,
∴三角形ADC是直角三角形,∠C=90°,
在直角三角形ABC中,,
∴BD=BC﹣DC=.
21.解:∵两个正方形木板的面积分别为18dm2和32dm2,
∴这两个正方形的边长分别为:=3(dm),=4(dm),
∴剩余木料的面积为:(4﹣3)×3=×3=6(dm2).
22.解:(1)如图所示,AB=2,AC=BC==,则△ABC的周长是:AB+AC+BC=2+2;
(2)设BC边上高是h,则
BCh=32﹣×2×2﹣2××1×3=4,
即:×h=4,
解得h=.
一.选择题(共8小题)
1.如图,从一个大正方形中可以裁去面积为8cm2和32cm2的两个小正方形,则大正方形的边长为( )
A. B. C. D.
2.已知两条线段的长分别为和,当第三条线段的长取何值时,这三条线段能围成一个直角三角形( )
A.2 B.4 C.2或4 D.
3.在数学课上,老师将一长方形纸片的长增加,宽增加,就成为了一个面积为192cm2的正方形,则原长方形纸片的面积为( )
A.18cm2 B.20cm2 C.36cm2 D.48cm2
4.如图,已知阴影部分是一个正方形,AB=4,∠B=45°,此正方形的面积( )
A.16 B.8 C.4 D.2
5.已知△ABC的两边的长分别为2,5,则△ABC的周长不可能是( )
A.10 B.11 C.12 D.13
6.能与cm和cm的线段组成直角三角形的第三条线段的长是( )cm
A. B.1 C. D.或1
7.如图,在数学课上,老师用5个完全相同的小长方形在无重叠的情况下拼成了一个大长方形,已知小长方形的长为、宽为,下列是四位同学对该大长方形的判断,其中不正确的是( )
A.大长方形的长为6 B.大长方形的宽为5
C.大长方形的周长为11 D.大长方形的面积为90
8.△ABC的两边长分别为2和2,第三边上的高等于,则△ABC的面积是( )
A. B.2 C.或2 D.不能确定
二.填空题(共8小题)
9.如图,将长方形分成四个区域,其中A、B两正方形区域的面积分别是1和7,则剩余区域的面积是 .
10.一个直角三角形的两直角边长分别为cm和cm,则这个直角三角形的面积是 cm2.
11.如图,两个相邻的正方形ABCD和CEFG,其中B,C,E在同一条直线上,点D在CG上,它们的面积分别为27平方米和48平方米,则BE的长为 米.
12.已知△ABC中,AB=2AC,若AB边上的高为,△ABC的面积为2,则BC边的长为 .
13.如图,大、小两个正方形连在一起,大正方形的边长为10,小正方形的边长为6,则阴影部分的面积为 .
14.如图,在矩形ABCD中,不重叠地放上两张面积分别是5cm2和3cm2的正方形纸片BCHE和AEFG.矩形ABCD没被这两个正方形盖住的面积是 .
15.如图,D是等边三角形ABC中AC延长线上一点,连接BD,E是AB上一点,且DE=DB,若AD+AE=5,BE=,则BC= .
16.△ABC中,∠ACB=90°,∠A、∠B、∠C所对的边分别为a、b、c,已知它的周长为6+且c=.
(1)比较大小6 ;(2)△ABC的面积等于 .
三.解答题(共6小题)
17.一个矩形的长a=+,宽b=﹣.
(1)该矩形的面积= ,周长= ;
(2)求a2+b2+ab的值.
18.我国宋代的数学家秦九韶发现:若一个三角形的三边长分别为a,b,c,则这个三角形的面积为s=,其中p=(a+b+c).
如图1,在△ABC中,已知AB=9,AC=8,BC=7.
(1)求△ABC的面积;
(2)如图2,AD,BE为△ABC的两条角平分线,它们的交点为点I,求I到边BC的距离.
19.某居民小区有块形状为长方形ABCD的绿地,长方形绿地的长BC为8米,宽AB为米,现要在长方形绿地中修建一个长方形花坛(即图中阴影部分),长方形花坛的长为+1米,宽为﹣1米.
(1)长方形ABCD的周长是多少?(结果化为最简二次根式)
(2)除去修建花坛的地方.其它地方全修建成通道,通道上要铺上造价为6元/m2的地砖,要铺完整个通道,则购买地砖需要花费多少元?(结果化为最简二次根式)
20.如图,在△ADC中,是CD延长线上的点,连接AB.若,求BD的长.
21.有一块矩形木块,木工采用如图方式,求木板上截出两个面积分别为18dm2和32dm2的正方形木板,求剩余木料的面积.
22.如图,小正方形的边长为1,连接小正方形的三个顶点得到△ABC,解答下列问题:
(1)△ABC的周长是多少?
(2)BC边上高是多少?(结果用最简二次根式表示)
参考答案
一.选择题(共8小题)
1.解:从一个大正方形中裁去面积为 8cm2和 32cm2的两个小正方形,
则大正方形的边长是+=2+4=6.
故选:C.
2.解:设直角三角形的第三边为x,
当为斜边时,
由勾股定理可知:x2+6=10,
∴x=2,
当,为直角边时,
∴由勾股定理可知:6+10=x2,
∴x=4,
故选:C.
3.解:∵一个面积为192cm2的正方形纸片,边长为:8cm,
∴原矩形的长为:8﹣2=6(cm),宽为:8﹣7=(cm),
∴则原长方形纸片的面积为:(cm2).
故选:A.
4.解:∵AB=4,∠B=45°,
∴AC=AB?sin∠B=4×=2,
∴此正方形的面积为2×2=8.
故选:B.
5.解:设三角形的另一边长为x,
根据三角形三边关系可知:x<2+5,即x<7,
x>5﹣2,即x>3,
则3<x<7,
其周长L要满足:3+2+5<L<2+5+7,即10<L<14.
故选:D.
6.解:①是直角边时,第三边==cm,
②是斜边时,第三边==1cm,
所以,第三条线段的长是cm或1cm.
故选:D.
7.解:∵小长方形的长为=3、宽为=2,
∴大长方形的长为:,大长方形的宽为:,
大长方形的周长是:,大长方形的面积为:,
故选项C错误,选项A、B、D正确;
故选:C.
8.解:如图1,
根据题意,AB=2、AC=2,AD=,
∴BD==1,CD==3,
则S△ABC=×(1+3)×=2;
如图2,
S△ABC=×(3﹣1)×=,
故选:C.
二.填空题(共8小题)
9.解:∵A,B两正方形区域的面积分别是1和7,
∴A,B两正方形边长分别是1和,
故剩余区域的面积是:
(+1)﹣7﹣1
=7+﹣8
=﹣1.
故答案为:﹣1.
10.解:这个直角三角形的面积=cm2,
故答案为:2
11.∵正方形ABCD的面积为27,
∴BC=.
∵正方形CEFG的面积为48,
∴CE=.
∴BE=BC+CE=.
故答案为:.
12.解:AB=2×2÷=4,
则AC=AB=2,
在Rt△ADC中,AD===1
如图1,BD=AB﹣AD=4﹣1=3,
在Rt△CDB中,BC===2;
如图2,BD=AB+AD=4+1=5,
在Rt△CDB中,BC===2.
则BC边的长为2或2.
故答案为:2或2.
13.解:由图形可得,阴影部分的面积为:×10×10=50.
故答案为:50.
14.解:∵两张正方形纸片的面积分别为5cm2和3cm2,
∴它们的边长分别为cm和cm,
∴AB=(+)cm,BC=cm,
∴矩形ABCD没被这两个正方形盖住的面积是=﹣5﹣3=(﹣3)cm2,
故答案为:(﹣3)cm2.
15.解:过D作DF⊥AB于F,交BC于G,
∵DE=DB,
∴EF=BF=,
设AE=x,
∴AD=5﹣x,AF=AE+EF=x+,
∵△ABC是等边三角形,
∴∠A=60°,
∴∠ADF=30°,
∴AD=2AF,
即5﹣x=2(x+),
∴x=,
∴BC=AB=+=,
故答案为:.
16.解:(1)∵6=,
∴6>;
(2)∵∠ACB=90°,∠A、∠B、∠C所对的边分别为a、b、c,
它的周长为6+且c=,
∴a+b=6,a2+b2=c2=26,
∴(a+b)2=36,
∴a2+b2+2ab=36,
∴2ab=10,
∴ab=2.5.
故答案为:>,2.5.
三.解答题(共6小题)
17.解:(1)矩形的面积=ab==6﹣5=1;
周长=2(a+b)==4.
故答案为:1;.
(2)由(1)得:a+b=2,ab=1,
原式=(a+b)2﹣ab
=
=23.
18.解:(1)由题意得:p===12,
∴S△ABC===12;
(2)连接IC,过点I分别作AB、BC、AC边的垂线交AB、BC、AC于点M、Q、N,
由角平分线的性质定理可知:IM=IQ=IN,
观察图形易知:S△ABC=S△ABI+S△BCI+S△ACI===12,
∴=12,
解得:IQ=,
故I到边BC的距离为:.
19.解:(1)长方形ABCD的周长=2×()=2(8+7)=16+14(米),
答:长方形ABCD的周长是16+14(米),
(2)通道的面积=
=56﹣(13﹣1)
=56(平方米),
购买地砖需要花费=6×(56)=336﹣72(元).
答:购买地砖需要花费336﹣72元;
20.解:在,
∵AC2+DC2=3+5=AD2,
∴三角形ADC是直角三角形,∠C=90°,
在直角三角形ABC中,,
∴BD=BC﹣DC=.
21.解:∵两个正方形木板的面积分别为18dm2和32dm2,
∴这两个正方形的边长分别为:=3(dm),=4(dm),
∴剩余木料的面积为:(4﹣3)×3=×3=6(dm2).
22.解:(1)如图所示,AB=2,AC=BC==,则△ABC的周长是:AB+AC+BC=2+2;
(2)设BC边上高是h,则
BCh=32﹣×2×2﹣2××1×3=4,
即:×h=4,
解得h=.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
