人教版数学八年级上册11.2.1.1三角形的内角(3)教案
文档属性
| 名称 | 人教版数学八年级上册11.2.1.1三角形的内角(3)教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 98.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 00:00:00 | ||
图片预览

文档简介
人教版八年级上册11.2.1《三角形的内角》教学设计
一、教材分析
(一)教材的地位和作用
《三角形的内角》内容选自人教版九年义务教育八年级上册第十一章第二节第一课时.
“三角形的内角和等于180°”是三角形的一个重要性质,它从“角”的角度刻画了三角形的特征,也是进一步学习《多边形内角和》及其它几何知识的基础.
三角形内角和定理的证明以平行线的相关知识为基础,通过剪图、拼图来获得添加辅助线的思路和方法,为后继的学习奠定了基础,这种探究也体现了由实验几何到论证几何的研究过程!
(二)教学目标
基于对教材以上的认识及课程标准的要求,我拟定本节课的教学目标为:
1.
知识与技能:探索并证明三角形内角和定理;能运用三角形内角和定理
解决简单问题.
2.
过程与方法:通过拼图实践、合作探索、交流,培养学生的逻辑推理、大胆猜想、动手实践等能力.
3.情感、态度与价值观:在良好的师生关系下,建立轻松的学习氛围,使学生乐于学,在数学活动中获得成功的体验,增强自信心,在合作学习中增强集体责任感.
(三)教学重难点:
1.重点:探索并证明三角形内角和定理,体会证明的必要性.
2.难点:如何添加辅助线证明三角形内角和定理.
二、学情分析
处于这个年龄段的学生有能力自己动手,并乐于尝试、探索、思考、交流与合作,同时具有一定的分析、归纳、总结能力,渴望体验成功的喜悦.
因而老师有必要给学生充分的空间,同时注意问题的开放性与可扩展性.
基于以上情况,我确立了本节课的教法和学法:
三、教法、学法
(一)教法
基于本节课的特点和八年级学生的心理特征,我采用了“自学-议论-引导”的模式展开教学.
本节课采用多媒体辅助教学,提高课堂效率.
(二)学法
学生通过拼图初步得出证明思路,小组内讨论,寻求采用多种方法来证明三角形内角和定理,通过基础练习、提高练习和拓展练习发掘不同层次学生的不同能力,从而达到发展学生思维能力和自学能力的目的,发掘学生的创新精神.
四、教学准备
每个学生准备一个纸质三角形和剪刀.
五、教学过程设计
1.
探索并证明三角形内角和定理
问题1
用课件展示一副三角板,计算出它们的内角和都是180°,那所有的三角形内角和都是180°吗?为什么?
师生活动:学生回答,是的.
已预习的学生会模糊说出证明的方法,但绝大部分学生会说通过测量角度或老师告诉的.
追问1:通过测量若干个三角形的内角和就能说明全部吗?测量时没有误差吗?
师生活动:学生回答---不能,并且会存在误差.
追问2:到了初中,我们还能仅靠猜测就轻易得出结论吗?我们如何能得出“所有的三角形的三个内角的和都等于180°”这个结论呢?
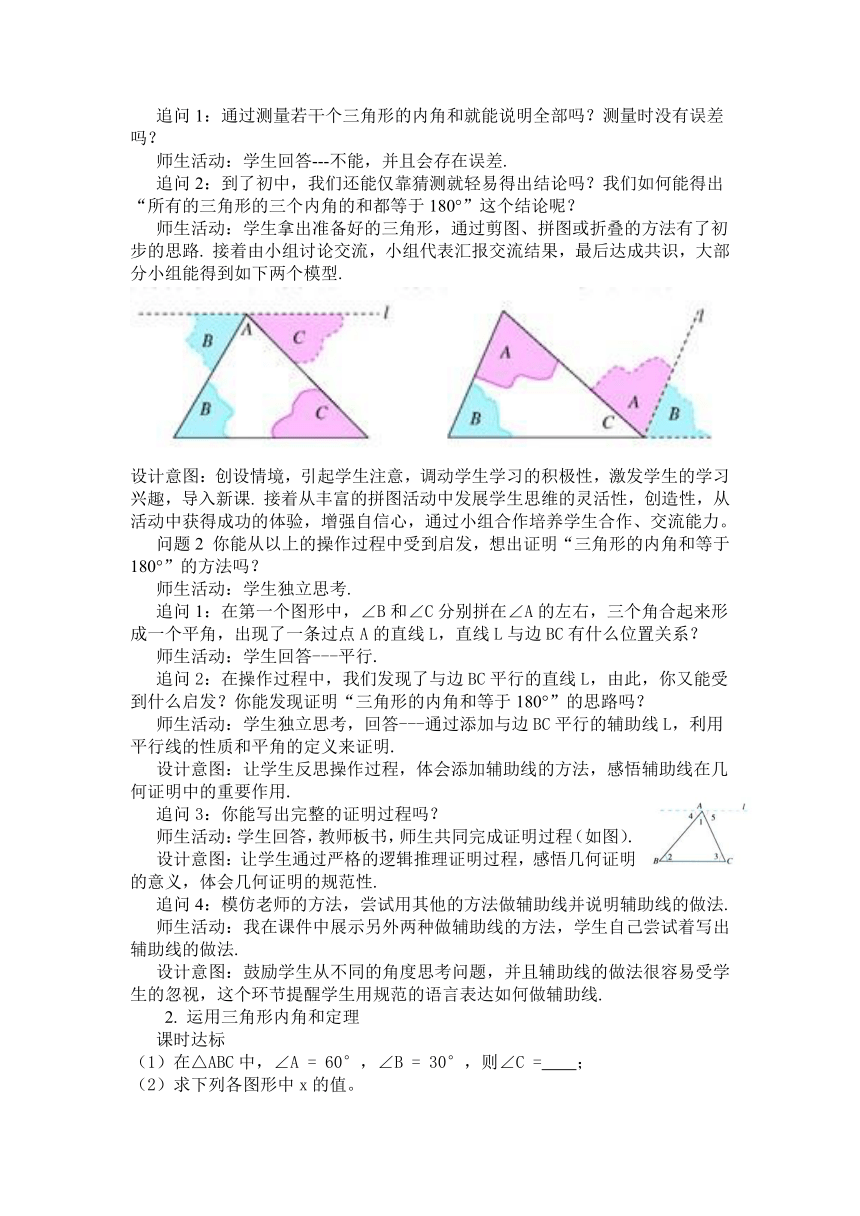
师生活动:学生拿出准备好的三角形,通过剪图、拼图或折叠的方法有了初步的思路.
接着由小组讨论交流,小组代表汇报交流结果,最后达成共识,大部分小组能得到如下两个模型.
设计意图:创设情境,引起学生注意,调动学生学习的积极性,激发学生的学习兴趣,导入新课.
接着从丰富的拼图活动中发展学生思维的灵活性,创造性,从活动中获得成功的体验,增强自信心,通过小组合作培养学生合作、交流能力。
问题2
你能从以上的操作过程中受到启发,想出证明“三角形的内角和等于180°”的方法吗?
师生活动:学生独立思考.
追问1:在第一个图形中,∠B和∠C分别拼在∠A的左右,三个角合起来形成一个平角,出现了一条过点A的直线L,直线L与边BC有什么位置关系?
师生活动:学生回答---平行.
追问2:在操作过程中,我们发现了与边BC平行的直线L,由此,你又能受到什么启发?你能发现证明“三角形的内角和等于180°”的思路吗?
师生活动:学生独立思考,回答---通过添加与边BC平行的辅助线L,利用平行线的性质和平角的定义来证明.
设计意图:让学生反思操作过程,体会添加辅助线的方法,感悟辅助线在几何证明中的重要作用.
追问3:你能写出完整的证明过程吗?
师生活动:学生回答,教师板书,师生共同完成证明过程(如图).
设计意图:让学生通过严格的逻辑推理证明过程,感悟几何证明的意义,体会几何证明的规范性.
追问4:模仿老师的方法,尝试用其他的方法做辅助线并说明辅助线的做法.
师生活动:我在课件中展示另外两种做辅助线的方法,学生自己尝试着写出辅助线的做法.
设计意图:鼓励学生从不同的角度思考问题,并且辅助线的做法很容易受学生的忽视,这个环节提醒学生用规范的语言表达如何做辅助线.
2.
运用三角形内角和定理
课时达标
(1)在△ABC中,∠A
=
60°,∠B
=
30°,则∠C
=
;
(2)求下列各图形中x的值。
1
x=
②
x=
师生活动:(1)独立思考并完成;(2)采用口答解决.
设计意图:这两题简单的呈现三角形内角和的运用,促进学生进一步巩固定理内容.
应用新知
(1)三角形的三个内角之比为1∶3∶5,那么这个三角形的最大内角为
;
(2)在△ABC中,∠A
=
40°,∠B
=∠C,则∠B
=
;
(3)在△ABC中,∠A
=∠B
=
4∠C,则∠C
=
;
师生活动:(1)独立思考并完成;(2)口头回答做法;(3)呈现准备好的答案.
设计意图:这三题灵活运用了三角形的内角和定理,并且和方程结合起来,拓宽学生的思维能力.
例题解析
例1、如图,在△ABC中,∠BAC
=40°,∠B
=75°,AD是△ABC的角平分线.
求∠ADB的度数.
师生活动:(1)教师引导学生分析解题思路;(2)师生共同完成板书,规范解题.
设计意图:运用三角形内角和定理求相关角的度数,并学着规范板书.
变式练习
如图,在△ABC中,∠B
=45°,∠C
=75°,AD是△ABC的角平分线.求∠ADB的度数.
师生活动:(1)学生独立思考完成,一名学生板书;(2)由板书学生讲解思路和过程,师生一起评阅、质疑.
设计意图:这个题只是例1的变式练习,一方面照顾学困生学会模仿,另一方面教学生灵活思考,懂得举一反三.
拓展提高
如图,已知AC//DE,若∠ABC=45°,
∠E
=70°,
∠D=85°,求∠A与∠ABD的度数。
师生活动:(1)学生独立思考完成,一名学生板书;(2)由板书学生讲解思路和过程,师生一起评阅、质疑.
设计意图:由于本班是数学成绩较好的班级,学生接受能力较好,避免“吃不饱”的现象,学生自己讲解、质疑、得出答案,整个过程会有很大的成就感,激发学生对数学挑战的欲望.
3.
小结
教师与学生一起回顾本节课所学的主要内容,并请学生回答以下问题:
(1)
本节课学习了哪些主要内容?
(2)
你是怎么找到三角形内角和定理的证明思路的?
设计意图:通过小结,使学生梳理本节课所学内容,掌握本节课的核心——三角形内角和定理,进一步回顾证明思路,体会辅助线在几何证明中的作用.
4.
布置作业
必做题:习题11.2第1、4、10题.
选做题:至少用两种方法解习题11.2第7题.
5.
板书设计
三角形的内角和
已知:△ABC中
解:
∵AD是△ABC的角平分线
求证:∠A+∠B+∠C=180°.
∴∠DAB=∠CAB=20°
证明:过点A做直线L//BC
在△ABC中
∴∠2=∠4
∠3=∠5
∠ADB=180°-∠B-∠DAB
∵∠1+∠4+∠5=180°
=180°-75°-20°
∴∠1+∠2+∠3=180°
=85°
教师备课札记
一、教材分析
(一)教材的地位和作用
《三角形的内角》内容选自人教版九年义务教育八年级上册第十一章第二节第一课时.
“三角形的内角和等于180°”是三角形的一个重要性质,它从“角”的角度刻画了三角形的特征,也是进一步学习《多边形内角和》及其它几何知识的基础.
三角形内角和定理的证明以平行线的相关知识为基础,通过剪图、拼图来获得添加辅助线的思路和方法,为后继的学习奠定了基础,这种探究也体现了由实验几何到论证几何的研究过程!
(二)教学目标
基于对教材以上的认识及课程标准的要求,我拟定本节课的教学目标为:
1.
知识与技能:探索并证明三角形内角和定理;能运用三角形内角和定理
解决简单问题.
2.
过程与方法:通过拼图实践、合作探索、交流,培养学生的逻辑推理、大胆猜想、动手实践等能力.
3.情感、态度与价值观:在良好的师生关系下,建立轻松的学习氛围,使学生乐于学,在数学活动中获得成功的体验,增强自信心,在合作学习中增强集体责任感.
(三)教学重难点:
1.重点:探索并证明三角形内角和定理,体会证明的必要性.
2.难点:如何添加辅助线证明三角形内角和定理.
二、学情分析
处于这个年龄段的学生有能力自己动手,并乐于尝试、探索、思考、交流与合作,同时具有一定的分析、归纳、总结能力,渴望体验成功的喜悦.
因而老师有必要给学生充分的空间,同时注意问题的开放性与可扩展性.
基于以上情况,我确立了本节课的教法和学法:
三、教法、学法
(一)教法
基于本节课的特点和八年级学生的心理特征,我采用了“自学-议论-引导”的模式展开教学.
本节课采用多媒体辅助教学,提高课堂效率.
(二)学法
学生通过拼图初步得出证明思路,小组内讨论,寻求采用多种方法来证明三角形内角和定理,通过基础练习、提高练习和拓展练习发掘不同层次学生的不同能力,从而达到发展学生思维能力和自学能力的目的,发掘学生的创新精神.
四、教学准备
每个学生准备一个纸质三角形和剪刀.
五、教学过程设计
1.
探索并证明三角形内角和定理
问题1
用课件展示一副三角板,计算出它们的内角和都是180°,那所有的三角形内角和都是180°吗?为什么?
师生活动:学生回答,是的.
已预习的学生会模糊说出证明的方法,但绝大部分学生会说通过测量角度或老师告诉的.
追问1:通过测量若干个三角形的内角和就能说明全部吗?测量时没有误差吗?
师生活动:学生回答---不能,并且会存在误差.
追问2:到了初中,我们还能仅靠猜测就轻易得出结论吗?我们如何能得出“所有的三角形的三个内角的和都等于180°”这个结论呢?
师生活动:学生拿出准备好的三角形,通过剪图、拼图或折叠的方法有了初步的思路.
接着由小组讨论交流,小组代表汇报交流结果,最后达成共识,大部分小组能得到如下两个模型.
设计意图:创设情境,引起学生注意,调动学生学习的积极性,激发学生的学习兴趣,导入新课.
接着从丰富的拼图活动中发展学生思维的灵活性,创造性,从活动中获得成功的体验,增强自信心,通过小组合作培养学生合作、交流能力。
问题2
你能从以上的操作过程中受到启发,想出证明“三角形的内角和等于180°”的方法吗?
师生活动:学生独立思考.
追问1:在第一个图形中,∠B和∠C分别拼在∠A的左右,三个角合起来形成一个平角,出现了一条过点A的直线L,直线L与边BC有什么位置关系?
师生活动:学生回答---平行.
追问2:在操作过程中,我们发现了与边BC平行的直线L,由此,你又能受到什么启发?你能发现证明“三角形的内角和等于180°”的思路吗?
师生活动:学生独立思考,回答---通过添加与边BC平行的辅助线L,利用平行线的性质和平角的定义来证明.
设计意图:让学生反思操作过程,体会添加辅助线的方法,感悟辅助线在几何证明中的重要作用.
追问3:你能写出完整的证明过程吗?
师生活动:学生回答,教师板书,师生共同完成证明过程(如图).
设计意图:让学生通过严格的逻辑推理证明过程,感悟几何证明的意义,体会几何证明的规范性.
追问4:模仿老师的方法,尝试用其他的方法做辅助线并说明辅助线的做法.
师生活动:我在课件中展示另外两种做辅助线的方法,学生自己尝试着写出辅助线的做法.
设计意图:鼓励学生从不同的角度思考问题,并且辅助线的做法很容易受学生的忽视,这个环节提醒学生用规范的语言表达如何做辅助线.
2.
运用三角形内角和定理
课时达标
(1)在△ABC中,∠A
=
60°,∠B
=
30°,则∠C
=
;
(2)求下列各图形中x的值。
1
x=
②
x=
师生活动:(1)独立思考并完成;(2)采用口答解决.
设计意图:这两题简单的呈现三角形内角和的运用,促进学生进一步巩固定理内容.
应用新知
(1)三角形的三个内角之比为1∶3∶5,那么这个三角形的最大内角为
;
(2)在△ABC中,∠A
=
40°,∠B
=∠C,则∠B
=
;
(3)在△ABC中,∠A
=∠B
=
4∠C,则∠C
=
;
师生活动:(1)独立思考并完成;(2)口头回答做法;(3)呈现准备好的答案.
设计意图:这三题灵活运用了三角形的内角和定理,并且和方程结合起来,拓宽学生的思维能力.
例题解析
例1、如图,在△ABC中,∠BAC
=40°,∠B
=75°,AD是△ABC的角平分线.
求∠ADB的度数.
师生活动:(1)教师引导学生分析解题思路;(2)师生共同完成板书,规范解题.
设计意图:运用三角形内角和定理求相关角的度数,并学着规范板书.
变式练习
如图,在△ABC中,∠B
=45°,∠C
=75°,AD是△ABC的角平分线.求∠ADB的度数.
师生活动:(1)学生独立思考完成,一名学生板书;(2)由板书学生讲解思路和过程,师生一起评阅、质疑.
设计意图:这个题只是例1的变式练习,一方面照顾学困生学会模仿,另一方面教学生灵活思考,懂得举一反三.
拓展提高
如图,已知AC//DE,若∠ABC=45°,
∠E
=70°,
∠D=85°,求∠A与∠ABD的度数。
师生活动:(1)学生独立思考完成,一名学生板书;(2)由板书学生讲解思路和过程,师生一起评阅、质疑.
设计意图:由于本班是数学成绩较好的班级,学生接受能力较好,避免“吃不饱”的现象,学生自己讲解、质疑、得出答案,整个过程会有很大的成就感,激发学生对数学挑战的欲望.
3.
小结
教师与学生一起回顾本节课所学的主要内容,并请学生回答以下问题:
(1)
本节课学习了哪些主要内容?
(2)
你是怎么找到三角形内角和定理的证明思路的?
设计意图:通过小结,使学生梳理本节课所学内容,掌握本节课的核心——三角形内角和定理,进一步回顾证明思路,体会辅助线在几何证明中的作用.
4.
布置作业
必做题:习题11.2第1、4、10题.
选做题:至少用两种方法解习题11.2第7题.
5.
板书设计
三角形的内角和
已知:△ABC中
解:
∵AD是△ABC的角平分线
求证:∠A+∠B+∠C=180°.
∴∠DAB=∠CAB=20°
证明:过点A做直线L//BC
在△ABC中
∴∠2=∠4
∠3=∠5
∠ADB=180°-∠B-∠DAB
∵∠1+∠4+∠5=180°
=180°-75°-20°
∴∠1+∠2+∠3=180°
=85°
教师备课札记
