人教版数学八年级上册11.2.1.2三角形内角和定理应用教案
文档属性
| 名称 | 人教版数学八年级上册11.2.1.2三角形内角和定理应用教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 140.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 00:00:00 | ||
图片预览

文档简介
11.2三角形的内角和(一)
教学任务分析
教学目标
知识目标
探究并掌握三角形内角和定理,并能应用三角形内角和定理解决一些简单的实际问题.
能力目标
经历观察、操作、推理、交流,发展推理能力和有条理的表达能力.
情感态度与价值观目标
学会多角度寻求解决问题的途径,在操作中进行自觉思考,积累数学探索的经验.
重点
三角形内角和定理.
难点
三角形内角和定理的推理过程
.
教学过程设计
问题与情景
师生行为
设计意图
[活动1]动手操作,引入新知
问题1
:我们已经知道,任意一个三角形的三个内角和等于180°.那么怎样证明这个结论呢?
问题2:将纸片上的△ABC三个内角剪下,随意将它们拼合在一起,你有几种拼法?经过拼合你能发现什么?
剪拼法:在纸上画出一个三角形,并将它的内角剪下来,拼在一起,就得到一个平角,请同学们动手做一做并进行监督指导.
通过动手操作,充分发挥学生的主动性和创新能力.
问题与情景
师生行为
设计意图
[活动2]
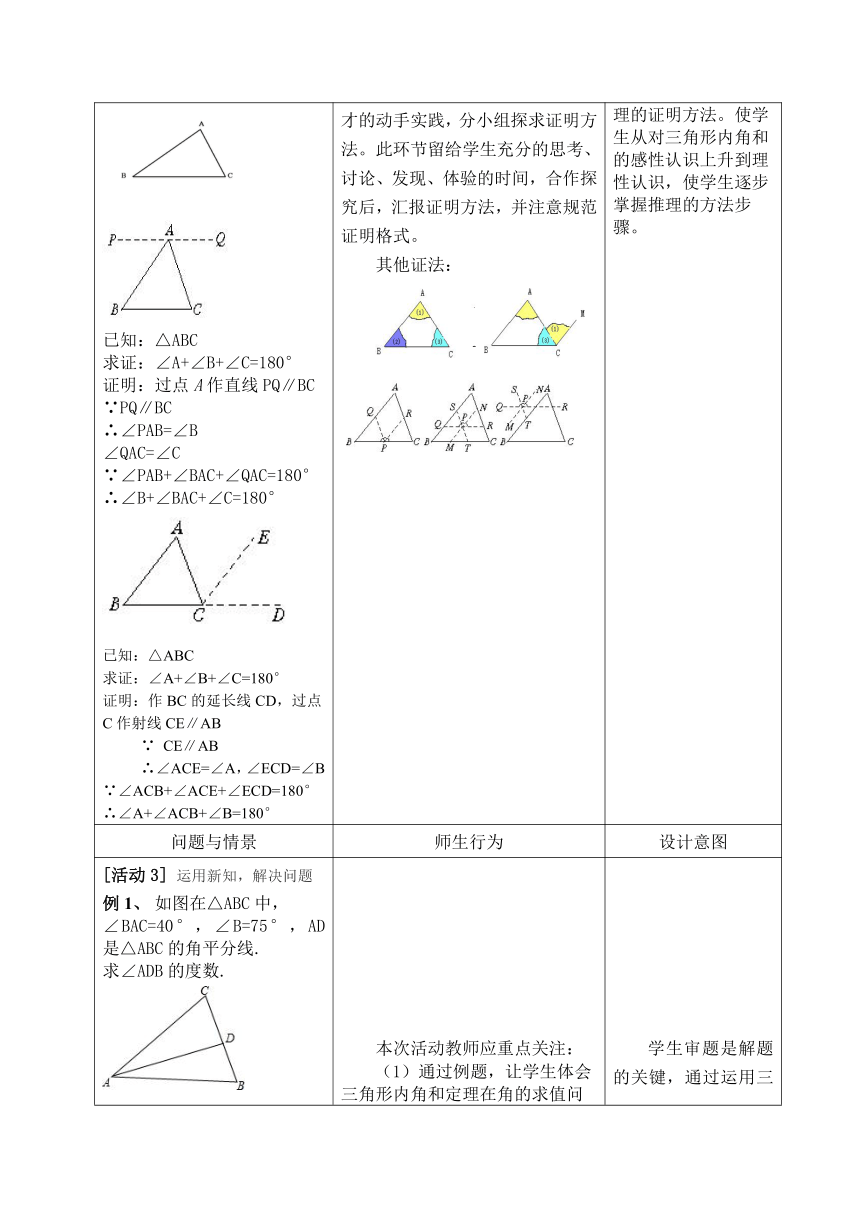
探究新知1.在小学里,用什么方法得到三角形内角和的结论?2.想一想通过动手实验我们发现三角形的三个内角的和等于180°,这个结论是否正确呢?因为在测量或剪拼中都会有误差,可不可以用推理论证的方法来说明上面的结论的正确性呢?已知:
求证:
已知:△ABC求证:∠A+∠B+∠C=180°证明:过点A作直线PQ∥BC∵PQ∥BC∴∠PAB=∠B∠QAC=∠C∵∠PAB+∠BAC+∠QAC=180°∴∠B+∠BAC+∠C=180°已知:△ABC求证:∠A+∠B+∠C=180°证明:作BC的延长线CD,过点C作射线CE∥AB
∵
CE∥AB
∴∠ACE=∠A,∠ECD=∠B
∵∠ACB+∠ACE+∠ECD=180°∴∠A+∠ACB+∠B=180°
本次活动教师应重点关注:先帮助学生回忆命题证明的基本步骤,然后让学生独立完成画图、写出已知、求证的步骤,其他同学补充完善。下面让学生对照刚才的动手实践,分小组探求证明方法。此环节留给学生充分的思考、讨论、发现、体验的时间,合作探究后,汇报证明方法,并注意规范证明格式。其他证法:
在教师的引导下,从动手操作中发现三角形的内角和定理的证明方法。使学生从对三角形内角和的感性认识上升到理性认识,使学生逐步掌握推理的方法步骤。?
问题与情景
师生行为
设计意图
[活动3]
运用新知,解决问题
如图在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线.求∠ADB的度数.例2、如图,C岛在A岛的北偏东方向,B岛在A岛的北偏东方向,C岛在B岛的北偏西方向,从C岛看A、B两岛的视角是多少度?[同步训练一]如图,说出各图中∠1
的度数.2、(1)一个三角形中最多有
个直角?为什么?(2)一个三角形中最多有
个钝角?为什么?(3)任意一个三角形中,最大的一个角的度数至少为
.3、如图,从A处观测C处的仰角∠CAD=30°,从B处观测C处的仰角∠CBD=45°,从C处观测A、B两处的视角∠ACB是多少度?
本次活动教师应重点关注:(1)通过例题,让学生体会三角形内角和定理在角的求值问题中的应用,注意向学生分析解决问题的思路和方法。对解题步骤的规范要求,提高学生数学综合解题能力。(2)学生能否进行合理的推理验证.
学生审题是解题的关键,通过运用三角形内角和定理,学会解决一些简单的数学问题.
通过练习实现知识向能力的转化,让学生能主动尝试从数学的角度运用所学知识和方法寻求解决问题的策略,同时训练学生能清晰、有条理地表达自己的思考过程,做到言之有理、落笔有据的意识.
问题与情景
师生行为
设计意图
[活动4]
随堂检测1、课本16页1题.2、在△ABC中,(1)∠A:∠B:∠C=3:4:5,则∠B
=
.(2)∠B
=80°,∠A=3∠C,则∠A
=
.(3)∠B=∠A+10°,∠C=∠B+10°,则△ABC各内角的度数分别为
.3、如图,一种滑翔伞是左右对称的四边形ABCD,其中∠A=150°,∠B=∠D=40°.求∠C的度数.
积极思考:如图,∠1=∠2,∠3=∠4,(1)若∠A=100°,求x的值.(2)若∠A=n°,求x的值.
教师给出题目,学生审题,独立思考,先在课堂练习本上书写解答过程,然后举手回答或实物展台展示过程或黑板书写证明过程,教师和同学共同点评.
本次活动教师应重点关注:就学生解题过程中暴露出来问题有针对性的点评.
考察学生对本节课所学内容的理解情况.
问题与情景
师生行为
设计意图
[活动5]小结反思,布置作业(1)小结(2)作业:习题11.2
3,4,7,8,10
教师引导学生回忆本节课所学的知识.教师布置作业,学生按要求课外完成.
梳理学习内容,养成整理知识的习惯.通过布置课外作业,及时获知学生对本节课知识的掌握情况,适当的调整教学进度和教学方法,并对学习有困难的学生给与指导.
教学反思:本节课教学活动中我力求充分体现以下特点:以学生发展为本,以学生为主体,思维为主线的思想;充分关注学生的自主探究与合作交流;练习体现了层次性,知识技能得于落实和发展。教师是学生学习的组织者、引导者、合作者,而非知识的灌输者,因而对一个问题的解决不是要教师将现成的方法传授给学生,而是教给学生解决问题的策略,给学生一把在知识的海洋中行舟的桨,让学生在积极思考,大胆尝试,主动探索中,获取成功并体验成功的喜悦。
3
80°
50°
1
30°
105°
1
22°
1
(1)
(2)
(3)
A
B
D
C
40
°
40
°
150°
A
B
C
1
2
教学任务分析
教学目标
知识目标
探究并掌握三角形内角和定理,并能应用三角形内角和定理解决一些简单的实际问题.
能力目标
经历观察、操作、推理、交流,发展推理能力和有条理的表达能力.
情感态度与价值观目标
学会多角度寻求解决问题的途径,在操作中进行自觉思考,积累数学探索的经验.
重点
三角形内角和定理.
难点
三角形内角和定理的推理过程
.
教学过程设计
问题与情景
师生行为
设计意图
[活动1]动手操作,引入新知
问题1
:我们已经知道,任意一个三角形的三个内角和等于180°.那么怎样证明这个结论呢?
问题2:将纸片上的△ABC三个内角剪下,随意将它们拼合在一起,你有几种拼法?经过拼合你能发现什么?
剪拼法:在纸上画出一个三角形,并将它的内角剪下来,拼在一起,就得到一个平角,请同学们动手做一做并进行监督指导.
通过动手操作,充分发挥学生的主动性和创新能力.
问题与情景
师生行为
设计意图
[活动2]
探究新知1.在小学里,用什么方法得到三角形内角和的结论?2.想一想通过动手实验我们发现三角形的三个内角的和等于180°,这个结论是否正确呢?因为在测量或剪拼中都会有误差,可不可以用推理论证的方法来说明上面的结论的正确性呢?已知:
求证:
已知:△ABC求证:∠A+∠B+∠C=180°证明:过点A作直线PQ∥BC∵PQ∥BC∴∠PAB=∠B∠QAC=∠C∵∠PAB+∠BAC+∠QAC=180°∴∠B+∠BAC+∠C=180°已知:△ABC求证:∠A+∠B+∠C=180°证明:作BC的延长线CD,过点C作射线CE∥AB
∵
CE∥AB
∴∠ACE=∠A,∠ECD=∠B
∵∠ACB+∠ACE+∠ECD=180°∴∠A+∠ACB+∠B=180°
本次活动教师应重点关注:先帮助学生回忆命题证明的基本步骤,然后让学生独立完成画图、写出已知、求证的步骤,其他同学补充完善。下面让学生对照刚才的动手实践,分小组探求证明方法。此环节留给学生充分的思考、讨论、发现、体验的时间,合作探究后,汇报证明方法,并注意规范证明格式。其他证法:
在教师的引导下,从动手操作中发现三角形的内角和定理的证明方法。使学生从对三角形内角和的感性认识上升到理性认识,使学生逐步掌握推理的方法步骤。?
问题与情景
师生行为
设计意图
[活动3]
运用新知,解决问题
如图在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线.求∠ADB的度数.例2、如图,C岛在A岛的北偏东方向,B岛在A岛的北偏东方向,C岛在B岛的北偏西方向,从C岛看A、B两岛的视角是多少度?[同步训练一]如图,说出各图中∠1
的度数.2、(1)一个三角形中最多有
个直角?为什么?(2)一个三角形中最多有
个钝角?为什么?(3)任意一个三角形中,最大的一个角的度数至少为
.3、如图,从A处观测C处的仰角∠CAD=30°,从B处观测C处的仰角∠CBD=45°,从C处观测A、B两处的视角∠ACB是多少度?
本次活动教师应重点关注:(1)通过例题,让学生体会三角形内角和定理在角的求值问题中的应用,注意向学生分析解决问题的思路和方法。对解题步骤的规范要求,提高学生数学综合解题能力。(2)学生能否进行合理的推理验证.
学生审题是解题的关键,通过运用三角形内角和定理,学会解决一些简单的数学问题.
通过练习实现知识向能力的转化,让学生能主动尝试从数学的角度运用所学知识和方法寻求解决问题的策略,同时训练学生能清晰、有条理地表达自己的思考过程,做到言之有理、落笔有据的意识.
问题与情景
师生行为
设计意图
[活动4]
随堂检测1、课本16页1题.2、在△ABC中,(1)∠A:∠B:∠C=3:4:5,则∠B
=
.(2)∠B
=80°,∠A=3∠C,则∠A
=
.(3)∠B=∠A+10°,∠C=∠B+10°,则△ABC各内角的度数分别为
.3、如图,一种滑翔伞是左右对称的四边形ABCD,其中∠A=150°,∠B=∠D=40°.求∠C的度数.
积极思考:如图,∠1=∠2,∠3=∠4,(1)若∠A=100°,求x的值.(2)若∠A=n°,求x的值.
教师给出题目,学生审题,独立思考,先在课堂练习本上书写解答过程,然后举手回答或实物展台展示过程或黑板书写证明过程,教师和同学共同点评.
本次活动教师应重点关注:就学生解题过程中暴露出来问题有针对性的点评.
考察学生对本节课所学内容的理解情况.
问题与情景
师生行为
设计意图
[活动5]小结反思,布置作业(1)小结(2)作业:习题11.2
3,4,7,8,10
教师引导学生回忆本节课所学的知识.教师布置作业,学生按要求课外完成.
梳理学习内容,养成整理知识的习惯.通过布置课外作业,及时获知学生对本节课知识的掌握情况,适当的调整教学进度和教学方法,并对学习有困难的学生给与指导.
教学反思:本节课教学活动中我力求充分体现以下特点:以学生发展为本,以学生为主体,思维为主线的思想;充分关注学生的自主探究与合作交流;练习体现了层次性,知识技能得于落实和发展。教师是学生学习的组织者、引导者、合作者,而非知识的灌输者,因而对一个问题的解决不是要教师将现成的方法传授给学生,而是教给学生解决问题的策略,给学生一把在知识的海洋中行舟的桨,让学生在积极思考,大胆尝试,主动探索中,获取成功并体验成功的喜悦。
3
80°
50°
1
30°
105°
1
22°
1
(1)
(2)
(3)
A
B
D
C
40
°
40
°
150°
A
B
C
1
2
