图形的中心对称
图片预览




文档简介
(共25张PPT)
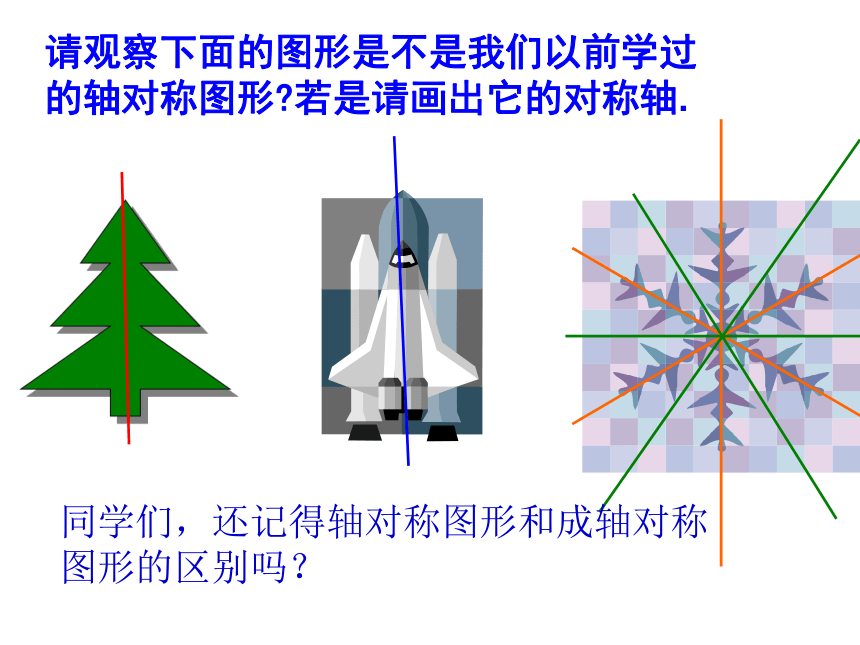
请观察下面的图形是不是我们以前学过的轴对称图形 若是请画出它的对称轴.
同学们,还记得轴对称图形和成轴对称图形的区别吗?
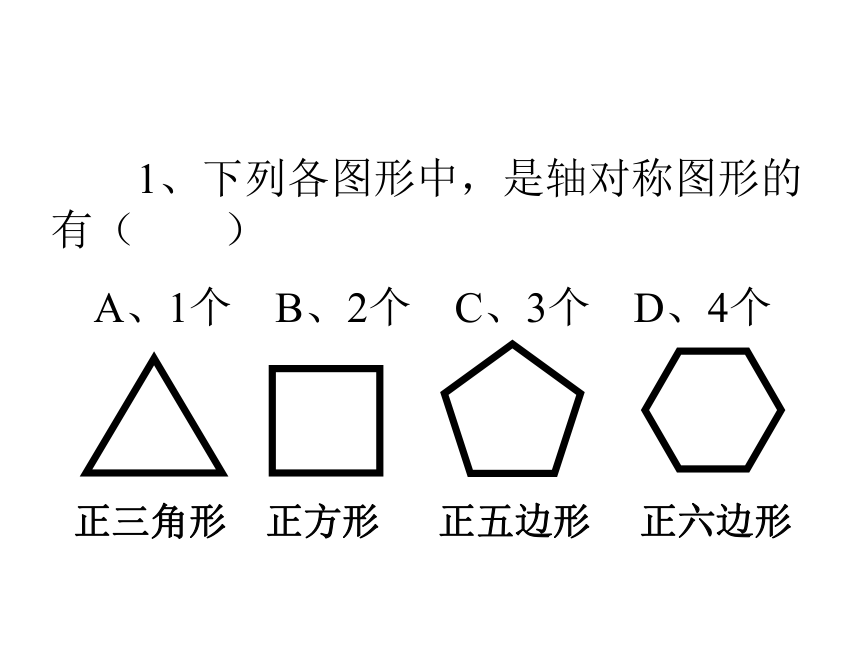
1、下列各图形中,是轴对称图形的有( )
A、1个 B、2个 C、3个 D、4个
正三角形 正方形 正五边形 正六边形
这三个图形各自旋转180°后都能与本身重合。
新课导入一
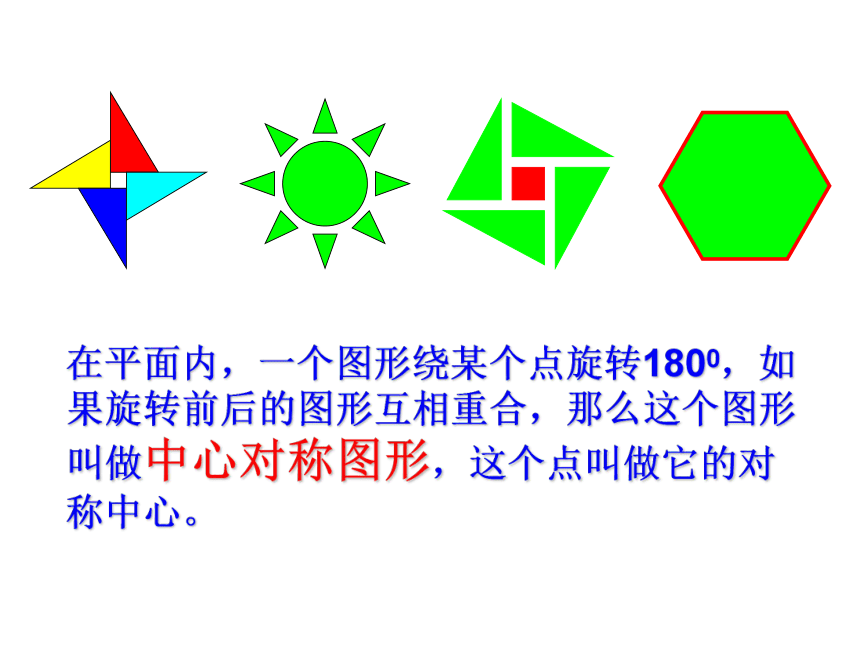
从图形变换的角度考虑,这些图形有什么共同的特征?
在平面内,一个图形绕某个点旋转1800,如果旋转前后的图形互相重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心。
O
B
A
C
D
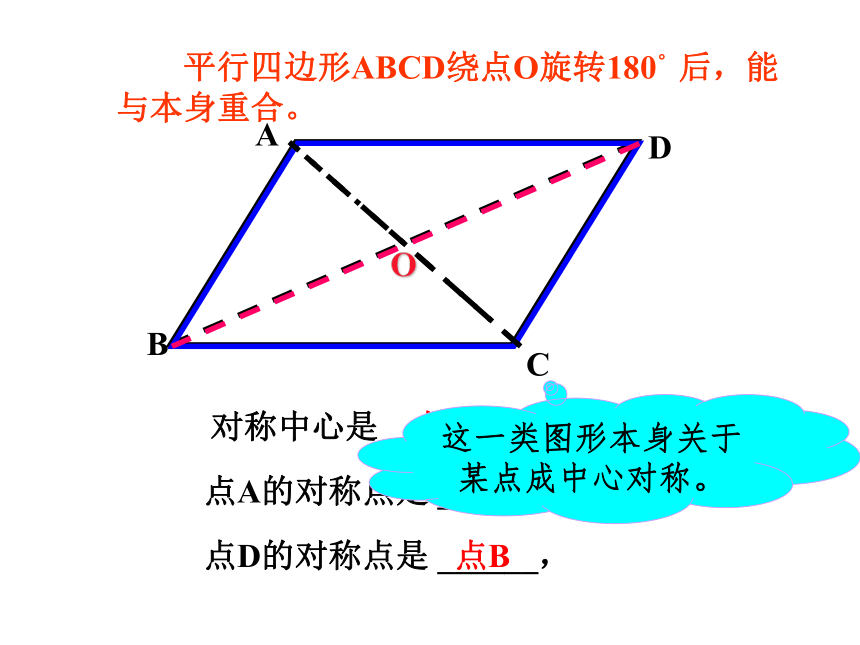
对称中心是 ______,
点O
点A的对称点是 ______,
点D的对称点是 ______,
点C
点B
平行四边形ABCD绕点O旋转180°后,能与本身重合。
这一类图形本身关于某点成中心对称。
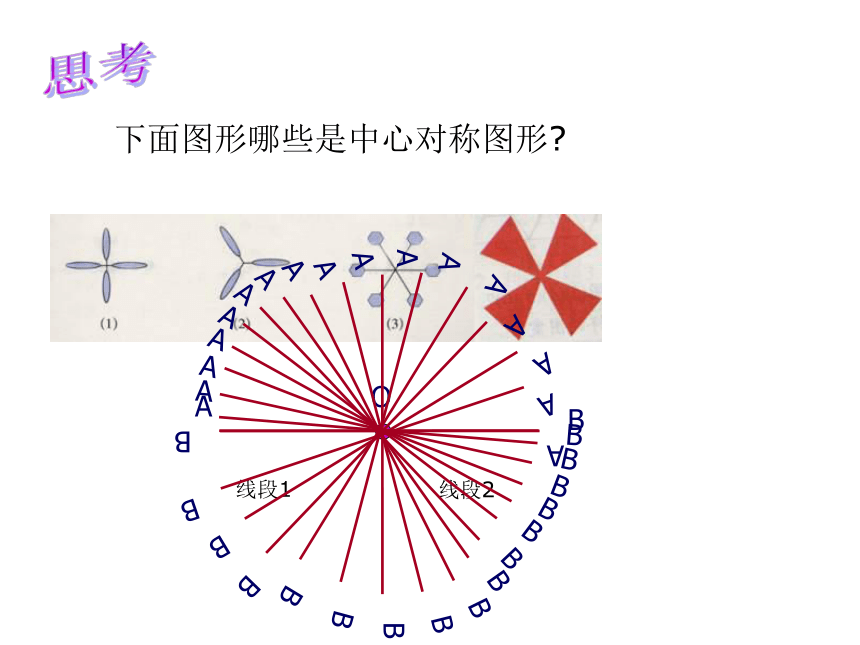
下面图形哪些是中心对称图形
线段1
线段2
O
A
B
A
B
A
B
A
B
A
B
A
B
A
B
A
B
A
B
A
B
A
B
A
B
A
B
A
B
A
B
A
B
A
B
下面的牌中哪些是中心对称图形?
小练习
√
√
√
轴对称图形与中心对称图形:
轴对称图形 中心对称图形
有一条对称轴——直线
有一个对称中心——点
图形沿轴对折
图形绕这个点旋转180O
对折部分与另一部分重合
旋转后与原图重合
连接中心对称图形上每一对对称点的线段都经过对称中心,且被对称中心平分
中心对称图形的性质:
(1)三角形是中心对称图形吗?
(2)正五边形是中心对称图形吗?
(3)正六边形是中心对称图形吗?
(4)除了平行四边形,你还能找到哪些多边形
是中心对称图形?
结论:中心对称的多边形很多,如边数为偶数
的正多边形都是中心对称图形。
(1)把其中一个图案绕点O旋转180°,你有什么发现
重合
重合
观察
(2)线段AC,BD相交于点O,OA=OC,OB=OD.把 △OCD绕点O旋转180°,你有什么发现
A
C
B
A
C
B
A
C
B
A
D
E
在平面内,一个图形绕某一定点旋转180°, 它能够和与另一个图形重合, 就说这两个图形关于这个点成中心对称,这个点叫做对称中心,旋转后两个图形上能够重合的点叫做关于对称中心的对称点.
A
D
E
讨论:中心对称与轴对称的区别:
畅所欲言:
你在生活中见到过中心对称的应用吗?
下图中△A′B′C′与△ABC关于点O是成中心对称的,你能从图中找到哪些等量关系
A’
B’
C’
A
B
C
O
(1)OA=OA′、OB=OB′、 OC=OC′
(2)△ABC≌△A′B′C′
A’
A
B
C
C’
B’
O
性质1 关于中心对称的两个图形是全等形。
∵ △ABC与△A`B`C`关
于点O成中心对称
∴ △ABC≌ △A`B`C`
性质2 关于中心对
称的两个图形,对称点的
连线都经过对称中心,并
且被对称中心平分。
∵△ABC与△A`B`C`关
于点O成中心对称
∴AA`、BB`、CC`经过点O
且 OA=OA`,OB=OB`,OC=OC`
名称 中心对称 中心对称图形
定义
性质
区别
联系
中心对称与中心对称图形的区别与联系
把一个图形绕着某一个点旋转180 ,如果他能够与另一个图形重合,那么就说这两个图形关于这点对称,这个点叫做对称中心,两个图形关于点对称也称中心对称,这两个图形中的对应点叫做关于中心的对称点
如果一个图形绕着一个点旋转180 后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心
①两个图形完全重合;
②对应点连线都经过对称中心,并且被对称中心平分
________
①两个图形的关系
②对称点在两个图形上
①具有某种性质的一个图形
②对称点在一个图形上
若把中心对称图形的两部分分别看作两图,则它们成中心对称。若把中心对称的两图看作一个整体,则成为中心对称图形。
巩固练习: 已知四边形ABCD和点O,画四边形A′B′C′D′,使它与已知四边形关于这一点对称。(2分钟)
A
B
A’
C’
B’
D’
D
O
C
四边形A1B1C1D1即为所求的图形。
1、中心对称图形,成中心对称的概念
2、 中心对称图形的基本性质
3、成中心对称图形的性质
4、中心对称图形,成中心对称
5、根据性质画图
1、在26个英文大写正体字母中,哪些字母是中心对称图形
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
达标检测
1、在26个英文大写正体字母中,哪些字母是中心对称图形
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
2 选择题:
⑴下列图形中即是轴对称图形又是中心对称图形的是( )
A 角 B 等边三角形 C 线段 D平行四边形
C
(2) 下列多边形中,是中心对称图形而不是轴对称图形的是( )
A平行四边形 B矩形 C菱形 D正方形
A
(3)已知:下列命题中真命题的个数是( )
①关于中心对称的两个图形一定不全等
②关于中心对称的两个图形是全等形
③两个全等的图形一定关于中心对称
A 0 B 1 C 2 D 3
B
3、 已知:如图ABCD和矩形AB’C’D’关于A点对称
求证:四边形BDB’D’是菱形
证明:∵矩形ABCD和矩形AB’C’D’
关于A点对称
∴AB=AB’ DA=D’A
∴四边形BDB’D’是平行四边形
∵DD’ ⊥BB’
∴ BDB’D’是菱形
A
B
C
D
B’
C’
D’
A’
B’
C’
O
A
B
C
4. 如图,已知等边三角形ABC和点O,
画△A’B’C’,使△A’B’C’和△ABC关于点O
成中心对称。
5、如图,已知△ABC与△A’B’C’中心对称,求出它们的对称中心O。
A
B
C
A’
B’
C’
请观察下面的图形是不是我们以前学过的轴对称图形 若是请画出它的对称轴.
同学们,还记得轴对称图形和成轴对称图形的区别吗?
1、下列各图形中,是轴对称图形的有( )
A、1个 B、2个 C、3个 D、4个
正三角形 正方形 正五边形 正六边形
这三个图形各自旋转180°后都能与本身重合。
新课导入一
从图形变换的角度考虑,这些图形有什么共同的特征?
在平面内,一个图形绕某个点旋转1800,如果旋转前后的图形互相重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心。
O
B
A
C
D
对称中心是 ______,
点O
点A的对称点是 ______,
点D的对称点是 ______,
点C
点B
平行四边形ABCD绕点O旋转180°后,能与本身重合。
这一类图形本身关于某点成中心对称。
下面图形哪些是中心对称图形
线段1
线段2
O
A
B
A
B
A
B
A
B
A
B
A
B
A
B
A
B
A
B
A
B
A
B
A
B
A
B
A
B
A
B
A
B
A
B
下面的牌中哪些是中心对称图形?
小练习
√
√
√
轴对称图形与中心对称图形:
轴对称图形 中心对称图形
有一条对称轴——直线
有一个对称中心——点
图形沿轴对折
图形绕这个点旋转180O
对折部分与另一部分重合
旋转后与原图重合
连接中心对称图形上每一对对称点的线段都经过对称中心,且被对称中心平分
中心对称图形的性质:
(1)三角形是中心对称图形吗?
(2)正五边形是中心对称图形吗?
(3)正六边形是中心对称图形吗?
(4)除了平行四边形,你还能找到哪些多边形
是中心对称图形?
结论:中心对称的多边形很多,如边数为偶数
的正多边形都是中心对称图形。
(1)把其中一个图案绕点O旋转180°,你有什么发现
重合
重合
观察
(2)线段AC,BD相交于点O,OA=OC,OB=OD.把 △OCD绕点O旋转180°,你有什么发现
A
C
B
A
C
B
A
C
B
A
D
E
在平面内,一个图形绕某一定点旋转180°, 它能够和与另一个图形重合, 就说这两个图形关于这个点成中心对称,这个点叫做对称中心,旋转后两个图形上能够重合的点叫做关于对称中心的对称点.
A
D
E
讨论:中心对称与轴对称的区别:
畅所欲言:
你在生活中见到过中心对称的应用吗?
下图中△A′B′C′与△ABC关于点O是成中心对称的,你能从图中找到哪些等量关系
A’
B’
C’
A
B
C
O
(1)OA=OA′、OB=OB′、 OC=OC′
(2)△ABC≌△A′B′C′
A’
A
B
C
C’
B’
O
性质1 关于中心对称的两个图形是全等形。
∵ △ABC与△A`B`C`关
于点O成中心对称
∴ △ABC≌ △A`B`C`
性质2 关于中心对
称的两个图形,对称点的
连线都经过对称中心,并
且被对称中心平分。
∵△ABC与△A`B`C`关
于点O成中心对称
∴AA`、BB`、CC`经过点O
且 OA=OA`,OB=OB`,OC=OC`
名称 中心对称 中心对称图形
定义
性质
区别
联系
中心对称与中心对称图形的区别与联系
把一个图形绕着某一个点旋转180 ,如果他能够与另一个图形重合,那么就说这两个图形关于这点对称,这个点叫做对称中心,两个图形关于点对称也称中心对称,这两个图形中的对应点叫做关于中心的对称点
如果一个图形绕着一个点旋转180 后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心
①两个图形完全重合;
②对应点连线都经过对称中心,并且被对称中心平分
________
①两个图形的关系
②对称点在两个图形上
①具有某种性质的一个图形
②对称点在一个图形上
若把中心对称图形的两部分分别看作两图,则它们成中心对称。若把中心对称的两图看作一个整体,则成为中心对称图形。
巩固练习: 已知四边形ABCD和点O,画四边形A′B′C′D′,使它与已知四边形关于这一点对称。(2分钟)
A
B
A’
C’
B’
D’
D
O
C
四边形A1B1C1D1即为所求的图形。
1、中心对称图形,成中心对称的概念
2、 中心对称图形的基本性质
3、成中心对称图形的性质
4、中心对称图形,成中心对称
5、根据性质画图
1、在26个英文大写正体字母中,哪些字母是中心对称图形
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
达标检测
1、在26个英文大写正体字母中,哪些字母是中心对称图形
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
2 选择题:
⑴下列图形中即是轴对称图形又是中心对称图形的是( )
A 角 B 等边三角形 C 线段 D平行四边形
C
(2) 下列多边形中,是中心对称图形而不是轴对称图形的是( )
A平行四边形 B矩形 C菱形 D正方形
A
(3)已知:下列命题中真命题的个数是( )
①关于中心对称的两个图形一定不全等
②关于中心对称的两个图形是全等形
③两个全等的图形一定关于中心对称
A 0 B 1 C 2 D 3
B
3、 已知:如图ABCD和矩形AB’C’D’关于A点对称
求证:四边形BDB’D’是菱形
证明:∵矩形ABCD和矩形AB’C’D’
关于A点对称
∴AB=AB’ DA=D’A
∴四边形BDB’D’是平行四边形
∵DD’ ⊥BB’
∴ BDB’D’是菱形
A
B
C
D
B’
C’
D’
A’
B’
C’
O
A
B
C
4. 如图,已知等边三角形ABC和点O,
画△A’B’C’,使△A’B’C’和△ABC关于点O
成中心对称。
5、如图,已知△ABC与△A’B’C’中心对称,求出它们的对称中心O。
A
B
C
A’
B’
C’
同课章节目录
