2020-2021学年贵州省黔南州八年级(下)期末数学试卷(word解析版)
文档属性
| 名称 | 2020-2021学年贵州省黔南州八年级(下)期末数学试卷(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-09 15:41:28 | ||
图片预览


文档简介
2020-2021学年贵州省黔南州八年级(下)期末数学试卷
一、选择题(每题2分,共24分)
1.=( )
A.﹣4 B.4 C.﹣2 D.2
2.一本笔记本5元,买x本共付y元,则5和y分别是( )
A.常量,常量 B.变量,变量 C.常量,变量 D.变量,常量
3.如图,在?ABCD中,若∠A=2∠B,则∠D的度数为( )
A.30° B.45° C.70° D.60°
4.下列运算正确的是( )
A. B. C. D.
5.第十六届中国国际文化产业博览交易会以“云上文博会”形式举办,各省通过搭建VR虚拟展馆的形式进行展览.在展会期间,很多有贵州地方特色的文化产业发展成果精彩亮相.借此机会,某手工艺术品展台通过网络平台销售了100件安顺奇石圆形摆件,销售情况统计如表:
直径(cm) 25 38 48 55 60
销量/件 22 28 20 13 17
则圆形摆件直径的众数为( )
A.43cm B.38cm C.48cm D.46cm
6.下列曲线中表示y是x的函数的是( )
A. B.
C. D.
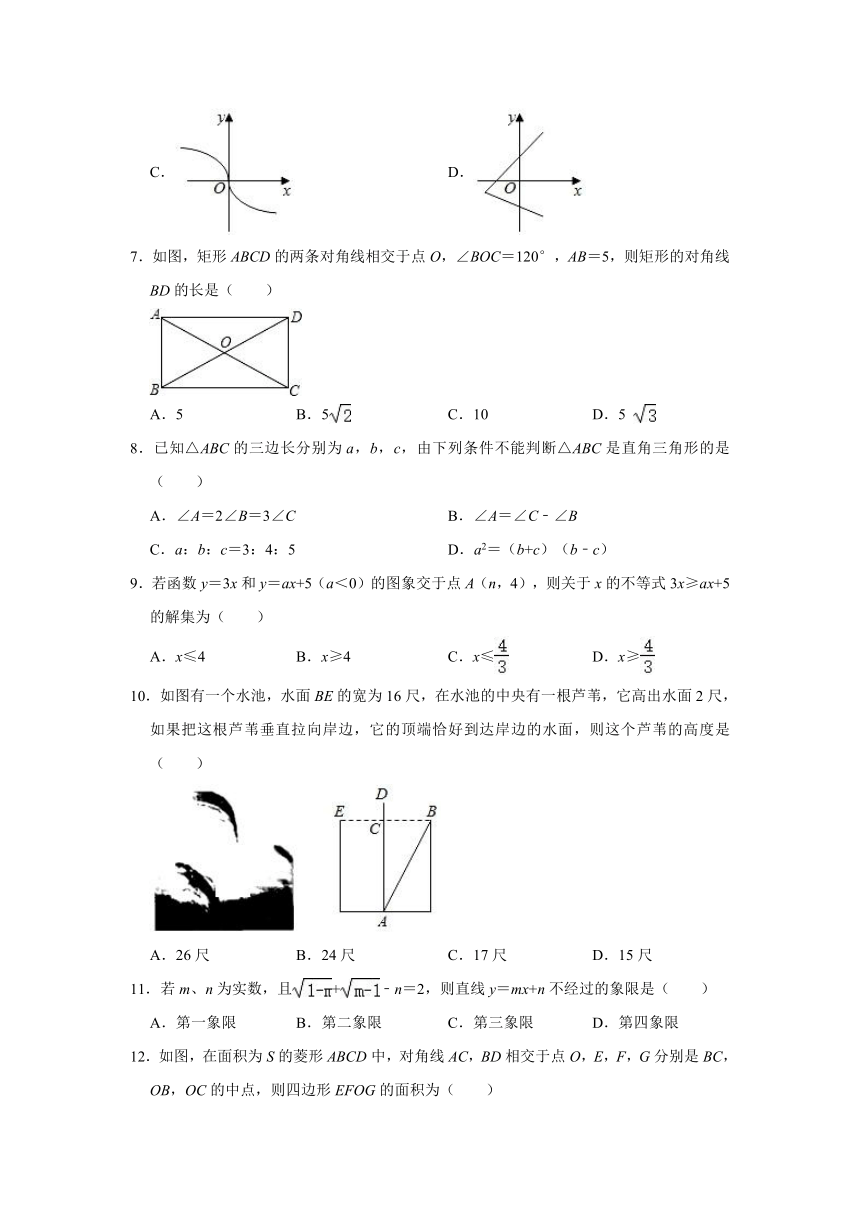
7.如图,矩形ABCD的两条对角线相交于点O,∠BOC=120°,AB=5,则矩形的对角线BD的长是( )
A.5 B.5 C.10 D.5
8.已知△ABC的三边长分别为a,b,c,由下列条件不能判断△ABC是直角三角形的是( )
A.∠A=2∠B=3∠C B.∠A=∠C﹣∠B
C.a:b:c=3:4:5 D.a2=(b+c)(b﹣c)
9.若函数y=3x和y=ax+5(a<0)的图象交于点A(n,4),则关于x的不等式3x≥ax+5的解集为( )
A.x≤4 B.x≥4 C.x≤ D.x≥
10.如图有一个水池,水面BE的宽为16尺,在水池的中央有一根芦苇,它高出水面2尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,则这个芦苇的高度是( )
A.26尺 B.24尺 C.17尺 D.15尺
11.若m、n为实数,且+﹣n=2,则直线y=mx+n不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
12.如图,在面积为S的菱形ABCD中,对角线AC,BD相交于点O,E,F,G分别是BC,OB,OC的中点,则四边形EFOG的面积为( )
A. B. C. D.
二、填空题(本大题4小題,每题3分,共12分)
13.函数y=的自变量x的取值范围是 .
14.将直线y=x+1向下平移4个单位后,所得直线的解析式是 .
15.在四边形ABCD中,AB=CD,要使四边形ABCD为平行四边形,则应添加的条件是(添加一个条件即可) .
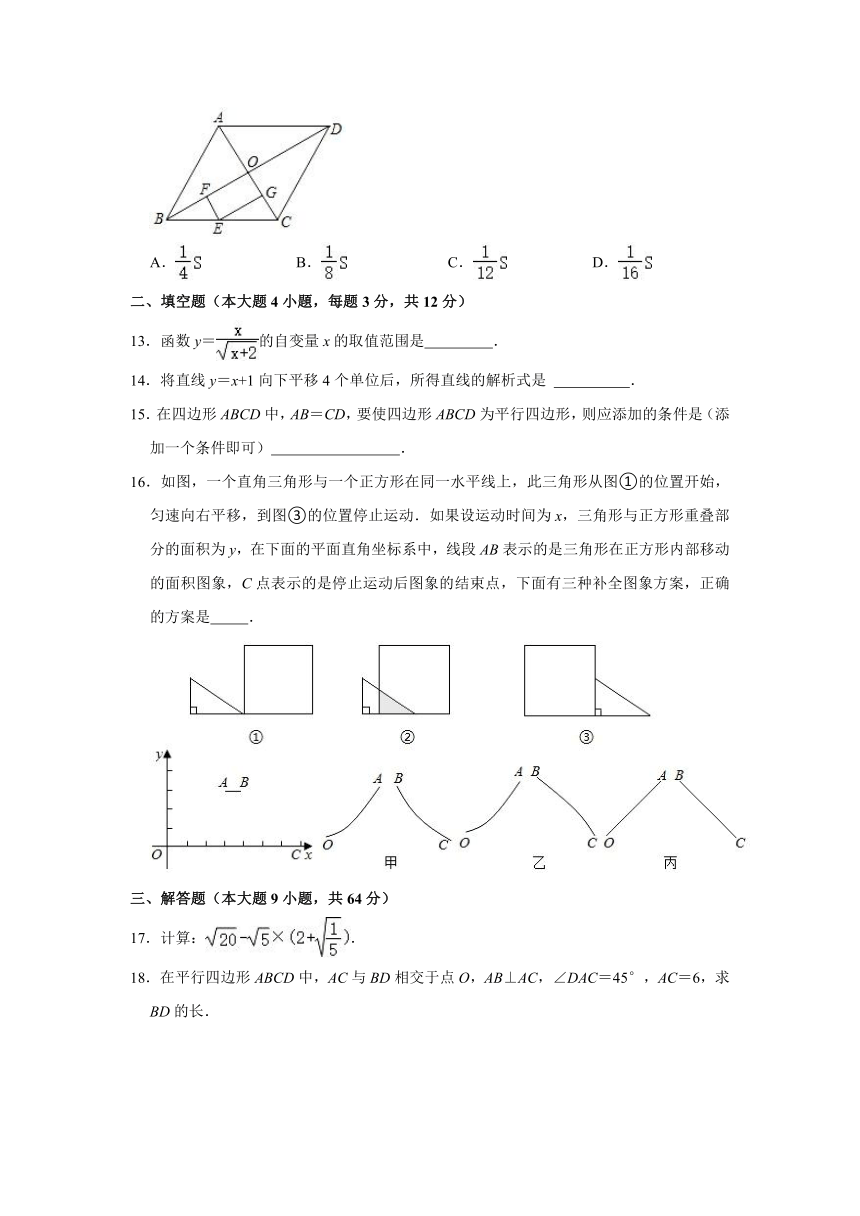
16.如图,一个直角三角形与一个正方形在同一水平线上,此三角形从图①的位置开始,匀速向右平移,到图③的位置停止运动.如果设运动时间为x,三角形与正方形重叠部分的面积为y,在下面的平面直角坐标系中,线段AB表示的是三角形在正方形内部移动的面积图象,C点表示的是停止运动后图象的结束点,下面有三种补全图象方案,正确的方案是 .
三、解答题(本大题9小题,共64分)
17.计算:.
18.在平行四边形ABCD中,AC与BD相交于点O,AB⊥AC,∠DAC=45°,AC=6,求BD的长.
19.在如图所示的平面直角坐标系中直接画出一次函数y=﹣x+2与y=﹣x﹣1的图象,并指出两条直线的位置关系.
20.老师在黑板上出示了这样一道题;化简.
嘉嘉的解法:原式=.
琪琪的解法:原式=.
(1)关于嘉嘉和琪琪的解法,说法的正确是 .
A.只有嘉嘉的解法正确;
B.只有琪琪的解法正确;
C.都正确;
D.都错误.
(2)请选择一种最适合你的方法化简.
21.直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).
(1)求直线AB的解析式;
(2)若直线AB上一点C在第一象限且点C的横坐标与纵坐标相等,求△BOC的面积.
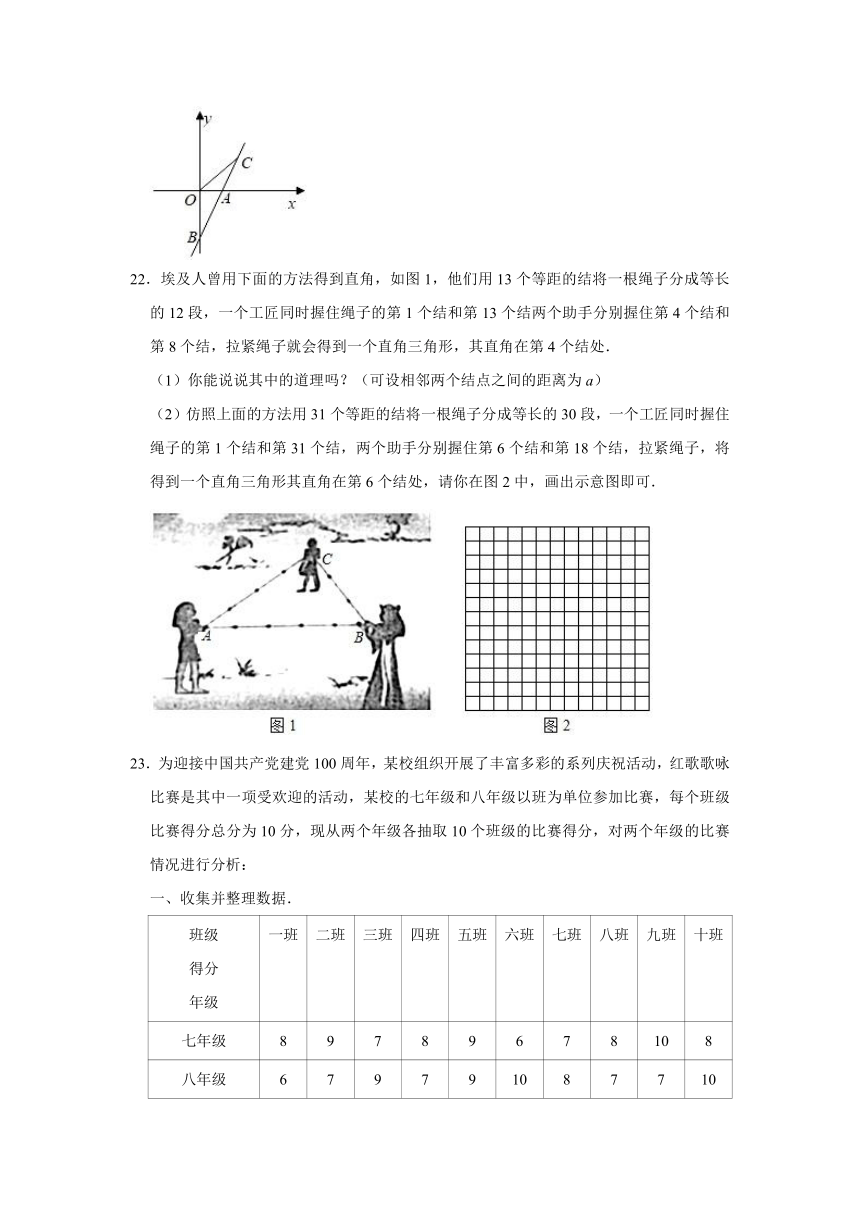
22.埃及人曾用下面的方法得到直角,如图1,他们用13个等距的结将一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结两个助手分别握住第4个结和第8个结,拉紧绳子就会得到一个直角三角形,其直角在第4个结处.
(1)你能说说其中的道理吗?(可设相邻两个结点之间的距离为a)
(2)仿照上面的方法用31个等距的结将一根绳子分成等长的30段,一个工匠同时握住绳子的第1个结和第31个结,两个助手分别握住第6个结和第18个结,拉紧绳子,将得到一个直角三角形其直角在第6个结处,请你在图2中,画出示意图即可.
23.为迎接中国共产党建党100周年,某校组织开展了丰富多彩的系列庆祝活动,红歌歌咏比赛是其中一项受欢迎的活动,某校的七年级和八年级以班为单位参加比赛,每个班级比赛得分总分为10分,现从两个年级各抽取10个班级的比赛得分,对两个年级的比赛情况进行分析:
一、收集并整理数据.
班级 得分
年级 一班 二班 三班 四班 五班 六班 七班 八班 九班 十班
七年级 8 9 7 8 9 6 7 8 10 8
八年级 6 7 9 7 9 10 8 7 7 10
二、分析数据.
平均数 众数 中位数 方差
七年级 a b 8 1.2
八年级 8 7 c 1.8
三、应用数据.
(1)a= ,b= ,c= .
(2)若规定9分及以上为优秀,请估计全校40个班级中,成绩优秀的班级共有几个班?
(3)你认为哪个年级的比赛成绩较好一些,请至少从以上统计的两个数据进行分析.
24.“又是一年春光好,植树添绿正当时”,进入春季后,全国各地开始大规模开展植树造林活动,贵州各地也正在积极响应.植树节当天,某校购买了A,B两种树苗共100棵进行种植,其中A种树苗的种植单价为30元,成活率为90%,B种树苗的种植单价为37元,成活率为95%.设购买A种树苗x棵,这批树苗种植后成活y棵,请解答下列问题.
(1)求出y与x之间的函数关系式.
(2)为保证这批树苗种植后至少成活93棵,求该校用于植树造林活动的总费用的最小值.
25.操作发现:
已知正方形ABCD的边长为1,在边BC,CD上任取一点P(不与顶点B,C,D重合),连接AP,分别过点D,B作DE⊥AP于点E,BF⊥AP于点F.
(1)如图1,当点P在CD上时,求证:BF=DE+EF.
(2)如图2,当点P在CD上时,过点C作CG⊥AP交AP的延长线于点G,试判断线段DE,BF,CG间的数量关系,并说明理由.
拓广探索:
(3)如图3,当点P在BC上时,过点C作CG⊥AP交AP的延长线于点G,请直接写出线段DE,BF,CG之间的数量关系,不用写理由.
参考答案
一、选择题(本大题12小题,每题2分,共24分)
1.=( )
A.﹣4 B.4 C.﹣2 D.2
【分析】利用二次根式的性质进行计算.
解:==4,
故选:B.
2.一本笔记本5元,买x本共付y元,则5和y分别是( )
A.常量,常量 B.变量,变量 C.常量,变量 D.变量,常量
【分析】在一个变化的过程中,数值发生变化的量称为变量,数值始终不变的量称为常量,所以5和y分别是常量,变量,据此判断即可.
解:一本笔记本5元,买x本共付y元,则5和y分别是常量,变量.
故选:C.
3.如图,在?ABCD中,若∠A=2∠B,则∠D的度数为( )
A.30° B.45° C.70° D.60°
【分析】由平行四边形的性质得出∠A+∠B=180°,再由已知条件∠A=2∠B,即可得出∠B的度数,再根据平行四边形的对角相等即可求出∠D的度数.
解:∵四边形ABCD是平行四边形,
∴AD∥BC,∠B=∠D,
∴∠A+∠B=180°,
∵∠A=2∠B,
∴2∠B+∠B=180°,
解得:∠B=60°;
∴∠D=60°,
故选:D.
4.下列运算正确的是( )
A. B. C. D.
【分析】根据二次根式的加法运算法则判断A,根据二次根式的减法计算法则判断B,根据二次根式的除法运算法则判断C,根据二次根式的乘法运算法则判断D.
解:A、与不是同类二次根式,不能合并计算,故此选项不符合题意;
B、2﹣5=﹣3,故此选项不符合题意;
C、,故此选项不符合题意;
D、,故此选项符合题意;
故选:D.
5.第十六届中国国际文化产业博览交易会以“云上文博会”形式举办,各省通过搭建VR虚拟展馆的形式进行展览.在展会期间,很多有贵州地方特色的文化产业发展成果精彩亮相.借此机会,某手工艺术品展台通过网络平台销售了100件安顺奇石圆形摆件,销售情况统计如表:
直径(cm) 25 38 48 55 60
销量/件 22 28 20 13 17
则圆形摆件直径的众数为( )
A.43cm B.38cm C.48cm D.46cm
【分析】根据众数的意义,结合统计表中的数据进行判断即可.
解:根据表格中的数据可知,销售圆形摆件中,直径为38cm的最多,共销售28件,
因此销售圆形摆件直径的众数为38cm,
故选:B.
6.下列曲线中表示y是x的函数的是( )
A. B.
C. D.
【分析】根据函数的定义解答即可.
解:A、不能表示y是x的函数,故此选项不合题意;
B、不能表示y是x的函数,故此选项不合题意;
C、能表示y是x的函数,故此选项合题意;
D、不能表示y是x的函数,故此选项不符合题意;
故选:C.
7.如图,矩形ABCD的两条对角线相交于点O,∠BOC=120°,AB=5,则矩形的对角线BD的长是( )
A.5 B.5 C.10 D.5
【分析】由矩形的性质可证△AOB为等边三角形,可求BO=AB的长,即可求BD的长.
解:∵四边形ABCD是矩形
∴AO=CO=BO=DO
∵∠BOC=120°
∴∠AOB=60°,且AO=BO
∴△ABO为等边三角形
∴AO=BO=AB=5
∴BD=10
故选:C.
8.已知△ABC的三边长分别为a,b,c,由下列条件不能判断△ABC是直角三角形的是( )
A.∠A=2∠B=3∠C B.∠A=∠C﹣∠B
C.a:b:c=3:4:5 D.a2=(b+c)(b﹣c)
【分析】根据三角形的内角和定理求出∠A的度数,即可判断选项A;根据三角形内角和定理求出∠C的度数,即可判断选项B;根据勾股定理的逆定理判定选项C和选项D即可.
解:设△ABC中,∠A的对边是a,∠B的对边是b,∠C的对边是c,
A.∵∠A=2∠B=3∠C,
∴∠B=∠A,∠C=∠A,
∵∠A+∠B+∠C=180°,
∴∠A+∠A+∠A=180°,
解得:∠A=()°,
∴△ABC不是直角三角形,故本选项符合题意;
B.∵∠A=∠C﹣∠B,
∴∠A+∠B=∠C,
∵∠A+∠B+∠C=180°,
∴2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,故本选项不符合题意;
C.∵a:b:c=3:4:5,
∴a2+b2=c2,
∴∠C=90°,
∴△ABC是直角三角形,故本选项不符合题意;
D∵a2=(b+c)(b﹣c),
∴a2=b2﹣c2,
即a2+c2=b2,
∴∠B=90°,
∴△ABC是直角三角形,故本选项不符合题意;
故选:A.
9.若函数y=3x和y=ax+5(a<0)的图象交于点A(n,4),则关于x的不等式3x≥ax+5的解集为( )
A.x≤4 B.x≥4 C.x≤ D.x≥
【分析】先利用正比例函数解析式确定A点坐标,然后利用函数图象,写出直线y=ax+5在直线y=3x下方所对应的自变量的范围即可.
解:把A(n,4)代入y=3x得3n=4,解得n=,则A(,4),
根据图象得,当x≥时,3x≥ax+5.
故选:D.
10.如图有一个水池,水面BE的宽为16尺,在水池的中央有一根芦苇,它高出水面2尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,则这个芦苇的高度是( )
A.26尺 B.24尺 C.17尺 D.15尺
【分析】先设水池的深度为x尺,则这根芦苇的长度为(x+2)尺,根据勾股定理可得方程x2+82=(x+2)2,再解即可.
解:设水池的深度为x尺,由题意得:
x2+82=(x+2)2,
解得:x=15,
所以x+2=17.
即:这个芦苇的高度是17尺.
故选:C.
11.若m、n为实数,且+﹣n=2,则直线y=mx+n不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【分析】根据非负数的性质求出m、n的值,再根据一次函数的性质得到答案.
解:因为m、n为实数,且+﹣n=2,
所以m﹣1=0,n+2=0,
即m=1,n=﹣2,
所以直线y=x﹣2经过一、三、四象限,不过第二象限,
故选:B.
12.如图,在面积为S的菱形ABCD中,对角线AC,BD相交于点O,E,F,G分别是BC,OB,OC的中点,则四边形EFOG的面积为( )
A. B. C. D.
【分析】连接OE,依据菱形的性质以及等腰三角形的性质,即可得到∠EFO,∠EGO,∠FOG都是直角,即可得到四边形OFEG是矩形;再根据菱形的面积即可得到矩形OFEG的面积.
解:如图所示,连接OE,
∵四边形ABCD是菱形,
∴∠BOC=90°,
又∵E是BC的中点,
∴OE=BE=CE,
又∵F,G分别是BO,CO的中点,
∴EF⊥OB,EG⊥OC,
∴四边形OGEF是矩形,
∵菱形ABCD的面积为S,
∴AC×BD=S,即AC×BD=2S,
∴四边形EFOG的面积=OG×OF=OC×OB=AC×BD=AC×BD=×2S=S.
故选:B.
二、填空题(本大题4小題,每题3分,共12分)
13.函数y=的自变量x的取值范围是 x>﹣2 .
【分析】根据被开方数是非负数,分母不能为零,可得答案.
解:由题意,得
x+2>0,
解得x>﹣2,
故答案为:x>﹣2.
14.将直线y=x+1向下平移4个单位后,所得直线的解析式是 y=x﹣3 .
【分析】直接根据“上加下减”的平移规律求解即可.
解:将直线y=x+1向下平移4个单位后,所得直线的解析式为y=x+1﹣4,即y=x﹣3.
故答案为y=x﹣3.
15.在四边形ABCD中,AB=CD,要使四边形ABCD为平行四边形,则应添加的条件是(添加一个条件即可) AB∥CD(答案不唯一) .
【分析】题中已知一组对边相等,可添加另一组对边相等,或已知的对边平行,都可.
解:根据平行四边形的判定,可添加AB∥CD(答案不唯一).
故答案为:AB∥CD(或AD=BC).
16.如图,一个直角三角形与一个正方形在同一水平线上,此三角形从图①的位置开始,匀速向右平移,到图③的位置停止运动.如果设运动时间为x,三角形与正方形重叠部分的面积为y,在下面的平面直角坐标系中,线段AB表示的是三角形在正方形内部移动的面积图象,C点表示的是停止运动后图象的结束点,下面有三种补全图象方案,正确的方案是 乙 .
【分析】当三角形从图①的位置开始,匀速向右平移到②的位置时,y=EF×DE=tanα?x2,该函数的表达式为开口向上的抛物线;直角三角形在正方形内部时,则y为常数,即为直角三角形的面积;当三角形通过正方形内部,匀速向右平移到②的位置时,同理可得:y=s﹣(x﹣a)2?tanα,进而求解.
解:设正方形的边长为a,直角三角形的面积为s,
①如下图,当三角形从图①的位置开始,匀速向右平移到②的位置时,如下图:
设重叠的图形为△DEF,∠DFE=α,
则EF=x,DE=EFtanα=xtanα,
则y=EF×DE=×x?xtanα=tanα?x2,该函数的表达式为开口向上的抛物线,
②当直角三角形在正方形内部时,
则y为常数,即为直角三角形的面积,对应函数图象AB段;
③当三角形通过正方形内部,匀速向右平移到②的位置时,
同理可得:y=s﹣(x﹣a)2?tanα=﹣tanα?x2+2a?tanα?x﹣a2tanα+s,该函数的表达式为开口向下的抛物线,
故答案为:乙.
三、解答题(本大题9小题,共64分)
17.计算:.
【分析】利用二次根式的性质进行化简,然后先算乘法,最后算加减.
解:原式=2﹣2﹣
=2﹣2﹣1
=﹣1.
18.在平行四边形ABCD中,AC与BD相交于点O,AB⊥AC,∠DAC=45°,AC=6,求BD的长.
【分析】根据平行四边形ABCD得到,BD=2OD,CD∥AB,由AB⊥AC,可得AC⊥CD,进而根据勾股定理即可得BD的长.
解:∵四边形ABCD是平行四边形,
∴,BD=2OD,CD∥AB,
∵AB⊥AC,
∴AC⊥CD,
∵∠DAC=45°,
∴CD=AC=6,
在Rt△COD中,,
∴.
19.在如图所示的平面直角坐标系中直接画出一次函数y=﹣x+2与y=﹣x﹣1的图象,并指出两条直线的位置关系.
【分析】首先分别作出y=﹣x+2与y=﹣x﹣1这两个函数的图象,然后根据图象可以直接观察即可.
解:一次函数y=﹣x+2经过点(2,0),(0,2),
y=﹣x﹣1的图象经过点(﹣1,0),(0,﹣1),
如图所示,
所以直线y=﹣x+2与直线y=﹣x﹣1平行.
20.老师在黑板上出示了这样一道题;化简.
嘉嘉的解法:原式=.
琪琪的解法:原式=.
(1)关于嘉嘉和琪琪的解法,说法的正确是 C .
A.只有嘉嘉的解法正确;
B.只有琪琪的解法正确;
C.都正确;
D.都错误.
(2)请选择一种最适合你的方法化简.
【分析】(1)嘉嘉利用平方差公式进行了二次根式分母有理化计算,琪琪利用平方差公式进行因式分解,然后再利用分式的基本性质进行约分,所以两位同学的解法都是正确的;
(2)利用平方差公式进行二次根式分母有理化计算.
解:(1)嘉嘉利用平方差公式进行了二次根式分母有理化计算,
琪琪利用平方差公式进行因式分解,然后再利用分式的基本性质进行约分,
两位同学的解法都是正确的,
故答案为:C;
(2)原式=
=
=
=.
21.直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).
(1)求直线AB的解析式;
(2)若直线AB上一点C在第一象限且点C的横坐标与纵坐标相等,求△BOC的面积.
【分析】(1)根据待定系数法即可求得;
(2)设点C的横坐标为m,代入解析式得m=2m﹣2,求得C(2,2),然后根据三角形面积公式求得即可.
解:(1)设直线AB的解析式为y=kx+b(k≠0).
将A(1,0),B(0,﹣2)代入解析式,得,
解得,
∴直线AB的解析式为y=2x﹣2;
(2)设点C的横坐标为m,代入得m=2m﹣2,解得m=2,
∴C(2,2),
∵B(0,﹣2),
∴S△BOC=×2×2=2.
22.埃及人曾用下面的方法得到直角,如图1,他们用13个等距的结将一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结两个助手分别握住第4个结和第8个结,拉紧绳子就会得到一个直角三角形,其直角在第4个结处.
(1)你能说说其中的道理吗?(可设相邻两个结点之间的距离为a)
(2)仿照上面的方法用31个等距的结将一根绳子分成等长的30段,一个工匠同时握住绳子的第1个结和第31个结,两个助手分别握住第6个结和第18个结,拉紧绳子,将得到一个直角三角形其直角在第6个结处,请你在图2中,画出示意图即可.
【分析】(1)根据勾股定理的逆定理进行证明即可;
(2)设相邻两个结点之间的距离为图中1个小正方形的边长,则此三角形三边的长分别为5、12、13,画出示意图即可.
解:(1)设相邻两个结点之间的距离为a,则此三角形三边的长分别为3a、4a、5a,
∵(3a)2+(4a)2=(5a)2,
∴以3a、4a、5a为边长的三角形是直角三角形;
(2)如图所示:
23.为迎接中国共产党建党100周年,某校组织开展了丰富多彩的系列庆祝活动,红歌歌咏比赛是其中一项受欢迎的活动,某校的七年级和八年级以班为单位参加比赛,每个班级比赛得分总分为10分,现从两个年级各抽取10个班级的比赛得分,对两个年级的比赛情况进行分析:
一、收集并整理数据.
班级 得分
年级 一班 二班 三班 四班 五班 六班 七班 八班 九班 十班
七年级 8 9 7 8 9 6 7 8 10 8
八年级 6 7 9 7 9 10 8 7 7 10
二、分析数据.
平均数 众数 中位数 方差
七年级 a b 8 1.2
八年级 8 7 c 1.8
三、应用数据.
(1)a= 8 ,b= 8 ,c= 7.5 .
(2)若规定9分及以上为优秀,请估计全校40个班级中,成绩优秀的班级共有几个班?
(3)你认为哪个年级的比赛成绩较好一些,请至少从以上统计的两个数据进行分析.
【分析】(1)根据中位数、平均数、众数的概念进行解答;
(2)总数乘以样本中9分及以上的班级数所占比例即可解答;
(3)分别从平均数和中位数、众数及方差的意义逐一分析可得.
解:(1)a=×(8+9+7+8+9+6+7+8+10+8)=8,
七年级10个班级的比赛得分8出现的最多,有4次,
∴b=8,
八年级10个班级的比赛得分从低到高重新排列为:6,7,7,7,7,8,9,9,10,10,
∴c=×(7+8)=7.5,
故答案为:8,8,7.5;
(2)估计全校40个班级中,成绩优秀的班级共:40×=14(个);
(3)从平均数看,七年级和八年级平均数相等,两个年级的平均成绩相等;
从中位数和众数看,七年级的中位数和众数大于八年级的中位数和众数,所以七年级高分的人数多于八年级高分人数,七年级的成绩较好;
从方差看,七年级的方差小于八年级的方差,所以七年级的成绩比八年级的成绩稳定,七年级的成绩较好;
综上可知,七年级的比赛成绩较好一些.
24.“又是一年春光好,植树添绿正当时”,进入春季后,全国各地开始大规模开展植树造林活动,贵州各地也正在积极响应.植树节当天,某校购买了A,B两种树苗共100棵进行种植,其中A种树苗的种植单价为30元,成活率为90%,B种树苗的种植单价为37元,成活率为95%.设购买A种树苗x棵,这批树苗种植后成活y棵,请解答下列问题.
(1)求出y与x之间的函数关系式.
(2)为保证这批树苗种植后至少成活93棵,求该校用于植树造林活动的总费用的最小值.
【分析】(1)设购买A种树苗x棵,则购买B种树苗(100﹣x)棵,根据成活y棵=A种树苗成活的棵树+B种树苗成活的棵树,即可求出y与x之间的函数关系式;
(2)根据这批树苗至少成活93棵,列出关于x的不等式,可求出x的范围,再根据总费用w=购买A种树苗的费用+种植A种树苗的费用得出w与x的函数关系式,利用一次函数的性质即可求解.
解:(1)设购买A种树苗x棵,则购买B种树苗(100﹣x)棵,由题意得:
y=90%x+95%×(100﹣x)=﹣0.05x+95(0≤x≤100);
(2)由题意,可得﹣0.05x+95≥93,
解得x≤40,
设总费用为w元,
由题意,得w=30x+37×(100﹣x)=﹣7x+3700,
∵﹣7<0,
∴w随x的增大而减小,
∴当x=40时,该校用于植树造林活动的总费用最少,最小值为:﹣7×40+3700=3420(元),
答:该校用于植树造林活动的总费用的最小值为3420元.
25.操作发现:
已知正方形ABCD的边长为1,在边BC,CD上任取一点P(不与顶点B,C,D重合),连接AP,分别过点D,B作DE⊥AP于点E,BF⊥AP于点F.
(1)如图1,当点P在CD上时,求证:BF=DE+EF.
(2)如图2,当点P在CD上时,过点C作CG⊥AP交AP的延长线于点G,试判断线段DE,BF,CG间的数量关系,并说明理由.
拓广探索:
(3)如图3,当点P在BC上时,过点C作CG⊥AP交AP的延长线于点G,请直接写出线段DE,BF,CG之间的数量关系,不用写理由.
【分析】(1)由DE⊥AP,BF⊥AP,可得∠AED=∠AFB=90°,进而可证△ADE≌△BAF(AAS),再根据全等三角形性质即可证得结论;
(2)如图2,过点C作CH⊥BF于点H,同(1)可证得△DAE≌△BCH(AAS),即可得出答案;
(3)如图3.过点C作CH⊥BF交BF的延长线于点H.再由四边形ABCD为正方形,可证得△DAE≌△BCH(AAS),进而可证四边形HFGC为矩形,即可得出答案.
解:(1)如图1,∵DE⊥AP,BF⊥AP,
∴∠AED=∠AFB=90°,
∴∠DAE+∠BAF=90°,∠BAF+∠ABF=90°,
∴∠DAE=∠ABF,而AB=AD,
∴△ADE≌△BAF(AAS),
∴DE=AF,AE=BF,
∵AE=AF+EF,
∴BF=DE+EF.
(2)线段DE、BF、CG间的数量关系是BF=DE+CG.
理由如下:
如图2,过点C作CH⊥BF于点H,
∵∠CHF=∠HFG=∠CGF=90°,
∴四边形HFGC为矩形,
∴CG=FH.
同(1)可证得△DAE≌△BCH(AAS),
∴DE=BH,
∴BF=FH+BH=CG+DE.
(3)DE=BF+CG.理由如下:
如图3.过点C作CH⊥BF交BF的延长线于点H.
则∠CHB=∠AED=90°,
∵四边形ABCD为正方形,
∴AD=BC,AD∥BC,
∴∠DAE=∠BGF,
∵DE⊥AP,BF⊥AP,CG⊥AP,
∴∠AED=∠BFP=∠CGF=90°,
∴∠DAE+∠ADE=∠BPF+∠CBH=90°,
∴∠ADE=∠CBH,
∴△DAE≌△BCH(AAS),
∴DE=BH.
∵∠BHC=∠HFG=∠CGF=90°,
∴四边形HFGC为矩形,
∴HF=CG,
∵BH=BF+HF,
∴DE=BF+CG.
一、选择题(每题2分,共24分)
1.=( )
A.﹣4 B.4 C.﹣2 D.2
2.一本笔记本5元,买x本共付y元,则5和y分别是( )
A.常量,常量 B.变量,变量 C.常量,变量 D.变量,常量
3.如图,在?ABCD中,若∠A=2∠B,则∠D的度数为( )
A.30° B.45° C.70° D.60°
4.下列运算正确的是( )
A. B. C. D.
5.第十六届中国国际文化产业博览交易会以“云上文博会”形式举办,各省通过搭建VR虚拟展馆的形式进行展览.在展会期间,很多有贵州地方特色的文化产业发展成果精彩亮相.借此机会,某手工艺术品展台通过网络平台销售了100件安顺奇石圆形摆件,销售情况统计如表:
直径(cm) 25 38 48 55 60
销量/件 22 28 20 13 17
则圆形摆件直径的众数为( )
A.43cm B.38cm C.48cm D.46cm
6.下列曲线中表示y是x的函数的是( )
A. B.
C. D.
7.如图,矩形ABCD的两条对角线相交于点O,∠BOC=120°,AB=5,则矩形的对角线BD的长是( )
A.5 B.5 C.10 D.5
8.已知△ABC的三边长分别为a,b,c,由下列条件不能判断△ABC是直角三角形的是( )
A.∠A=2∠B=3∠C B.∠A=∠C﹣∠B
C.a:b:c=3:4:5 D.a2=(b+c)(b﹣c)
9.若函数y=3x和y=ax+5(a<0)的图象交于点A(n,4),则关于x的不等式3x≥ax+5的解集为( )
A.x≤4 B.x≥4 C.x≤ D.x≥
10.如图有一个水池,水面BE的宽为16尺,在水池的中央有一根芦苇,它高出水面2尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,则这个芦苇的高度是( )
A.26尺 B.24尺 C.17尺 D.15尺
11.若m、n为实数,且+﹣n=2,则直线y=mx+n不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
12.如图,在面积为S的菱形ABCD中,对角线AC,BD相交于点O,E,F,G分别是BC,OB,OC的中点,则四边形EFOG的面积为( )
A. B. C. D.
二、填空题(本大题4小題,每题3分,共12分)
13.函数y=的自变量x的取值范围是 .
14.将直线y=x+1向下平移4个单位后,所得直线的解析式是 .
15.在四边形ABCD中,AB=CD,要使四边形ABCD为平行四边形,则应添加的条件是(添加一个条件即可) .
16.如图,一个直角三角形与一个正方形在同一水平线上,此三角形从图①的位置开始,匀速向右平移,到图③的位置停止运动.如果设运动时间为x,三角形与正方形重叠部分的面积为y,在下面的平面直角坐标系中,线段AB表示的是三角形在正方形内部移动的面积图象,C点表示的是停止运动后图象的结束点,下面有三种补全图象方案,正确的方案是 .
三、解答题(本大题9小题,共64分)
17.计算:.
18.在平行四边形ABCD中,AC与BD相交于点O,AB⊥AC,∠DAC=45°,AC=6,求BD的长.
19.在如图所示的平面直角坐标系中直接画出一次函数y=﹣x+2与y=﹣x﹣1的图象,并指出两条直线的位置关系.
20.老师在黑板上出示了这样一道题;化简.
嘉嘉的解法:原式=.
琪琪的解法:原式=.
(1)关于嘉嘉和琪琪的解法,说法的正确是 .
A.只有嘉嘉的解法正确;
B.只有琪琪的解法正确;
C.都正确;
D.都错误.
(2)请选择一种最适合你的方法化简.
21.直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).
(1)求直线AB的解析式;
(2)若直线AB上一点C在第一象限且点C的横坐标与纵坐标相等,求△BOC的面积.
22.埃及人曾用下面的方法得到直角,如图1,他们用13个等距的结将一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结两个助手分别握住第4个结和第8个结,拉紧绳子就会得到一个直角三角形,其直角在第4个结处.
(1)你能说说其中的道理吗?(可设相邻两个结点之间的距离为a)
(2)仿照上面的方法用31个等距的结将一根绳子分成等长的30段,一个工匠同时握住绳子的第1个结和第31个结,两个助手分别握住第6个结和第18个结,拉紧绳子,将得到一个直角三角形其直角在第6个结处,请你在图2中,画出示意图即可.
23.为迎接中国共产党建党100周年,某校组织开展了丰富多彩的系列庆祝活动,红歌歌咏比赛是其中一项受欢迎的活动,某校的七年级和八年级以班为单位参加比赛,每个班级比赛得分总分为10分,现从两个年级各抽取10个班级的比赛得分,对两个年级的比赛情况进行分析:
一、收集并整理数据.
班级 得分
年级 一班 二班 三班 四班 五班 六班 七班 八班 九班 十班
七年级 8 9 7 8 9 6 7 8 10 8
八年级 6 7 9 7 9 10 8 7 7 10
二、分析数据.
平均数 众数 中位数 方差
七年级 a b 8 1.2
八年级 8 7 c 1.8
三、应用数据.
(1)a= ,b= ,c= .
(2)若规定9分及以上为优秀,请估计全校40个班级中,成绩优秀的班级共有几个班?
(3)你认为哪个年级的比赛成绩较好一些,请至少从以上统计的两个数据进行分析.
24.“又是一年春光好,植树添绿正当时”,进入春季后,全国各地开始大规模开展植树造林活动,贵州各地也正在积极响应.植树节当天,某校购买了A,B两种树苗共100棵进行种植,其中A种树苗的种植单价为30元,成活率为90%,B种树苗的种植单价为37元,成活率为95%.设购买A种树苗x棵,这批树苗种植后成活y棵,请解答下列问题.
(1)求出y与x之间的函数关系式.
(2)为保证这批树苗种植后至少成活93棵,求该校用于植树造林活动的总费用的最小值.
25.操作发现:
已知正方形ABCD的边长为1,在边BC,CD上任取一点P(不与顶点B,C,D重合),连接AP,分别过点D,B作DE⊥AP于点E,BF⊥AP于点F.
(1)如图1,当点P在CD上时,求证:BF=DE+EF.
(2)如图2,当点P在CD上时,过点C作CG⊥AP交AP的延长线于点G,试判断线段DE,BF,CG间的数量关系,并说明理由.
拓广探索:
(3)如图3,当点P在BC上时,过点C作CG⊥AP交AP的延长线于点G,请直接写出线段DE,BF,CG之间的数量关系,不用写理由.
参考答案
一、选择题(本大题12小题,每题2分,共24分)
1.=( )
A.﹣4 B.4 C.﹣2 D.2
【分析】利用二次根式的性质进行计算.
解:==4,
故选:B.
2.一本笔记本5元,买x本共付y元,则5和y分别是( )
A.常量,常量 B.变量,变量 C.常量,变量 D.变量,常量
【分析】在一个变化的过程中,数值发生变化的量称为变量,数值始终不变的量称为常量,所以5和y分别是常量,变量,据此判断即可.
解:一本笔记本5元,买x本共付y元,则5和y分别是常量,变量.
故选:C.
3.如图,在?ABCD中,若∠A=2∠B,则∠D的度数为( )
A.30° B.45° C.70° D.60°
【分析】由平行四边形的性质得出∠A+∠B=180°,再由已知条件∠A=2∠B,即可得出∠B的度数,再根据平行四边形的对角相等即可求出∠D的度数.
解:∵四边形ABCD是平行四边形,
∴AD∥BC,∠B=∠D,
∴∠A+∠B=180°,
∵∠A=2∠B,
∴2∠B+∠B=180°,
解得:∠B=60°;
∴∠D=60°,
故选:D.
4.下列运算正确的是( )
A. B. C. D.
【分析】根据二次根式的加法运算法则判断A,根据二次根式的减法计算法则判断B,根据二次根式的除法运算法则判断C,根据二次根式的乘法运算法则判断D.
解:A、与不是同类二次根式,不能合并计算,故此选项不符合题意;
B、2﹣5=﹣3,故此选项不符合题意;
C、,故此选项不符合题意;
D、,故此选项符合题意;
故选:D.
5.第十六届中国国际文化产业博览交易会以“云上文博会”形式举办,各省通过搭建VR虚拟展馆的形式进行展览.在展会期间,很多有贵州地方特色的文化产业发展成果精彩亮相.借此机会,某手工艺术品展台通过网络平台销售了100件安顺奇石圆形摆件,销售情况统计如表:
直径(cm) 25 38 48 55 60
销量/件 22 28 20 13 17
则圆形摆件直径的众数为( )
A.43cm B.38cm C.48cm D.46cm
【分析】根据众数的意义,结合统计表中的数据进行判断即可.
解:根据表格中的数据可知,销售圆形摆件中,直径为38cm的最多,共销售28件,
因此销售圆形摆件直径的众数为38cm,
故选:B.
6.下列曲线中表示y是x的函数的是( )
A. B.
C. D.
【分析】根据函数的定义解答即可.
解:A、不能表示y是x的函数,故此选项不合题意;
B、不能表示y是x的函数,故此选项不合题意;
C、能表示y是x的函数,故此选项合题意;
D、不能表示y是x的函数,故此选项不符合题意;
故选:C.
7.如图,矩形ABCD的两条对角线相交于点O,∠BOC=120°,AB=5,则矩形的对角线BD的长是( )
A.5 B.5 C.10 D.5
【分析】由矩形的性质可证△AOB为等边三角形,可求BO=AB的长,即可求BD的长.
解:∵四边形ABCD是矩形
∴AO=CO=BO=DO
∵∠BOC=120°
∴∠AOB=60°,且AO=BO
∴△ABO为等边三角形
∴AO=BO=AB=5
∴BD=10
故选:C.
8.已知△ABC的三边长分别为a,b,c,由下列条件不能判断△ABC是直角三角形的是( )
A.∠A=2∠B=3∠C B.∠A=∠C﹣∠B
C.a:b:c=3:4:5 D.a2=(b+c)(b﹣c)
【分析】根据三角形的内角和定理求出∠A的度数,即可判断选项A;根据三角形内角和定理求出∠C的度数,即可判断选项B;根据勾股定理的逆定理判定选项C和选项D即可.
解:设△ABC中,∠A的对边是a,∠B的对边是b,∠C的对边是c,
A.∵∠A=2∠B=3∠C,
∴∠B=∠A,∠C=∠A,
∵∠A+∠B+∠C=180°,
∴∠A+∠A+∠A=180°,
解得:∠A=()°,
∴△ABC不是直角三角形,故本选项符合题意;
B.∵∠A=∠C﹣∠B,
∴∠A+∠B=∠C,
∵∠A+∠B+∠C=180°,
∴2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,故本选项不符合题意;
C.∵a:b:c=3:4:5,
∴a2+b2=c2,
∴∠C=90°,
∴△ABC是直角三角形,故本选项不符合题意;
D∵a2=(b+c)(b﹣c),
∴a2=b2﹣c2,
即a2+c2=b2,
∴∠B=90°,
∴△ABC是直角三角形,故本选项不符合题意;
故选:A.
9.若函数y=3x和y=ax+5(a<0)的图象交于点A(n,4),则关于x的不等式3x≥ax+5的解集为( )
A.x≤4 B.x≥4 C.x≤ D.x≥
【分析】先利用正比例函数解析式确定A点坐标,然后利用函数图象,写出直线y=ax+5在直线y=3x下方所对应的自变量的范围即可.
解:把A(n,4)代入y=3x得3n=4,解得n=,则A(,4),
根据图象得,当x≥时,3x≥ax+5.
故选:D.
10.如图有一个水池,水面BE的宽为16尺,在水池的中央有一根芦苇,它高出水面2尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,则这个芦苇的高度是( )
A.26尺 B.24尺 C.17尺 D.15尺
【分析】先设水池的深度为x尺,则这根芦苇的长度为(x+2)尺,根据勾股定理可得方程x2+82=(x+2)2,再解即可.
解:设水池的深度为x尺,由题意得:
x2+82=(x+2)2,
解得:x=15,
所以x+2=17.
即:这个芦苇的高度是17尺.
故选:C.
11.若m、n为实数,且+﹣n=2,则直线y=mx+n不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【分析】根据非负数的性质求出m、n的值,再根据一次函数的性质得到答案.
解:因为m、n为实数,且+﹣n=2,
所以m﹣1=0,n+2=0,
即m=1,n=﹣2,
所以直线y=x﹣2经过一、三、四象限,不过第二象限,
故选:B.
12.如图,在面积为S的菱形ABCD中,对角线AC,BD相交于点O,E,F,G分别是BC,OB,OC的中点,则四边形EFOG的面积为( )
A. B. C. D.
【分析】连接OE,依据菱形的性质以及等腰三角形的性质,即可得到∠EFO,∠EGO,∠FOG都是直角,即可得到四边形OFEG是矩形;再根据菱形的面积即可得到矩形OFEG的面积.
解:如图所示,连接OE,
∵四边形ABCD是菱形,
∴∠BOC=90°,
又∵E是BC的中点,
∴OE=BE=CE,
又∵F,G分别是BO,CO的中点,
∴EF⊥OB,EG⊥OC,
∴四边形OGEF是矩形,
∵菱形ABCD的面积为S,
∴AC×BD=S,即AC×BD=2S,
∴四边形EFOG的面积=OG×OF=OC×OB=AC×BD=AC×BD=×2S=S.
故选:B.
二、填空题(本大题4小題,每题3分,共12分)
13.函数y=的自变量x的取值范围是 x>﹣2 .
【分析】根据被开方数是非负数,分母不能为零,可得答案.
解:由题意,得
x+2>0,
解得x>﹣2,
故答案为:x>﹣2.
14.将直线y=x+1向下平移4个单位后,所得直线的解析式是 y=x﹣3 .
【分析】直接根据“上加下减”的平移规律求解即可.
解:将直线y=x+1向下平移4个单位后,所得直线的解析式为y=x+1﹣4,即y=x﹣3.
故答案为y=x﹣3.
15.在四边形ABCD中,AB=CD,要使四边形ABCD为平行四边形,则应添加的条件是(添加一个条件即可) AB∥CD(答案不唯一) .
【分析】题中已知一组对边相等,可添加另一组对边相等,或已知的对边平行,都可.
解:根据平行四边形的判定,可添加AB∥CD(答案不唯一).
故答案为:AB∥CD(或AD=BC).
16.如图,一个直角三角形与一个正方形在同一水平线上,此三角形从图①的位置开始,匀速向右平移,到图③的位置停止运动.如果设运动时间为x,三角形与正方形重叠部分的面积为y,在下面的平面直角坐标系中,线段AB表示的是三角形在正方形内部移动的面积图象,C点表示的是停止运动后图象的结束点,下面有三种补全图象方案,正确的方案是 乙 .
【分析】当三角形从图①的位置开始,匀速向右平移到②的位置时,y=EF×DE=tanα?x2,该函数的表达式为开口向上的抛物线;直角三角形在正方形内部时,则y为常数,即为直角三角形的面积;当三角形通过正方形内部,匀速向右平移到②的位置时,同理可得:y=s﹣(x﹣a)2?tanα,进而求解.
解:设正方形的边长为a,直角三角形的面积为s,
①如下图,当三角形从图①的位置开始,匀速向右平移到②的位置时,如下图:
设重叠的图形为△DEF,∠DFE=α,
则EF=x,DE=EFtanα=xtanα,
则y=EF×DE=×x?xtanα=tanα?x2,该函数的表达式为开口向上的抛物线,
②当直角三角形在正方形内部时,
则y为常数,即为直角三角形的面积,对应函数图象AB段;
③当三角形通过正方形内部,匀速向右平移到②的位置时,
同理可得:y=s﹣(x﹣a)2?tanα=﹣tanα?x2+2a?tanα?x﹣a2tanα+s,该函数的表达式为开口向下的抛物线,
故答案为:乙.
三、解答题(本大题9小题,共64分)
17.计算:.
【分析】利用二次根式的性质进行化简,然后先算乘法,最后算加减.
解:原式=2﹣2﹣
=2﹣2﹣1
=﹣1.
18.在平行四边形ABCD中,AC与BD相交于点O,AB⊥AC,∠DAC=45°,AC=6,求BD的长.
【分析】根据平行四边形ABCD得到,BD=2OD,CD∥AB,由AB⊥AC,可得AC⊥CD,进而根据勾股定理即可得BD的长.
解:∵四边形ABCD是平行四边形,
∴,BD=2OD,CD∥AB,
∵AB⊥AC,
∴AC⊥CD,
∵∠DAC=45°,
∴CD=AC=6,
在Rt△COD中,,
∴.
19.在如图所示的平面直角坐标系中直接画出一次函数y=﹣x+2与y=﹣x﹣1的图象,并指出两条直线的位置关系.
【分析】首先分别作出y=﹣x+2与y=﹣x﹣1这两个函数的图象,然后根据图象可以直接观察即可.
解:一次函数y=﹣x+2经过点(2,0),(0,2),
y=﹣x﹣1的图象经过点(﹣1,0),(0,﹣1),
如图所示,
所以直线y=﹣x+2与直线y=﹣x﹣1平行.
20.老师在黑板上出示了这样一道题;化简.
嘉嘉的解法:原式=.
琪琪的解法:原式=.
(1)关于嘉嘉和琪琪的解法,说法的正确是 C .
A.只有嘉嘉的解法正确;
B.只有琪琪的解法正确;
C.都正确;
D.都错误.
(2)请选择一种最适合你的方法化简.
【分析】(1)嘉嘉利用平方差公式进行了二次根式分母有理化计算,琪琪利用平方差公式进行因式分解,然后再利用分式的基本性质进行约分,所以两位同学的解法都是正确的;
(2)利用平方差公式进行二次根式分母有理化计算.
解:(1)嘉嘉利用平方差公式进行了二次根式分母有理化计算,
琪琪利用平方差公式进行因式分解,然后再利用分式的基本性质进行约分,
两位同学的解法都是正确的,
故答案为:C;
(2)原式=
=
=
=.
21.直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).
(1)求直线AB的解析式;
(2)若直线AB上一点C在第一象限且点C的横坐标与纵坐标相等,求△BOC的面积.
【分析】(1)根据待定系数法即可求得;
(2)设点C的横坐标为m,代入解析式得m=2m﹣2,求得C(2,2),然后根据三角形面积公式求得即可.
解:(1)设直线AB的解析式为y=kx+b(k≠0).
将A(1,0),B(0,﹣2)代入解析式,得,
解得,
∴直线AB的解析式为y=2x﹣2;
(2)设点C的横坐标为m,代入得m=2m﹣2,解得m=2,
∴C(2,2),
∵B(0,﹣2),
∴S△BOC=×2×2=2.
22.埃及人曾用下面的方法得到直角,如图1,他们用13个等距的结将一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结两个助手分别握住第4个结和第8个结,拉紧绳子就会得到一个直角三角形,其直角在第4个结处.
(1)你能说说其中的道理吗?(可设相邻两个结点之间的距离为a)
(2)仿照上面的方法用31个等距的结将一根绳子分成等长的30段,一个工匠同时握住绳子的第1个结和第31个结,两个助手分别握住第6个结和第18个结,拉紧绳子,将得到一个直角三角形其直角在第6个结处,请你在图2中,画出示意图即可.
【分析】(1)根据勾股定理的逆定理进行证明即可;
(2)设相邻两个结点之间的距离为图中1个小正方形的边长,则此三角形三边的长分别为5、12、13,画出示意图即可.
解:(1)设相邻两个结点之间的距离为a,则此三角形三边的长分别为3a、4a、5a,
∵(3a)2+(4a)2=(5a)2,
∴以3a、4a、5a为边长的三角形是直角三角形;
(2)如图所示:
23.为迎接中国共产党建党100周年,某校组织开展了丰富多彩的系列庆祝活动,红歌歌咏比赛是其中一项受欢迎的活动,某校的七年级和八年级以班为单位参加比赛,每个班级比赛得分总分为10分,现从两个年级各抽取10个班级的比赛得分,对两个年级的比赛情况进行分析:
一、收集并整理数据.
班级 得分
年级 一班 二班 三班 四班 五班 六班 七班 八班 九班 十班
七年级 8 9 7 8 9 6 7 8 10 8
八年级 6 7 9 7 9 10 8 7 7 10
二、分析数据.
平均数 众数 中位数 方差
七年级 a b 8 1.2
八年级 8 7 c 1.8
三、应用数据.
(1)a= 8 ,b= 8 ,c= 7.5 .
(2)若规定9分及以上为优秀,请估计全校40个班级中,成绩优秀的班级共有几个班?
(3)你认为哪个年级的比赛成绩较好一些,请至少从以上统计的两个数据进行分析.
【分析】(1)根据中位数、平均数、众数的概念进行解答;
(2)总数乘以样本中9分及以上的班级数所占比例即可解答;
(3)分别从平均数和中位数、众数及方差的意义逐一分析可得.
解:(1)a=×(8+9+7+8+9+6+7+8+10+8)=8,
七年级10个班级的比赛得分8出现的最多,有4次,
∴b=8,
八年级10个班级的比赛得分从低到高重新排列为:6,7,7,7,7,8,9,9,10,10,
∴c=×(7+8)=7.5,
故答案为:8,8,7.5;
(2)估计全校40个班级中,成绩优秀的班级共:40×=14(个);
(3)从平均数看,七年级和八年级平均数相等,两个年级的平均成绩相等;
从中位数和众数看,七年级的中位数和众数大于八年级的中位数和众数,所以七年级高分的人数多于八年级高分人数,七年级的成绩较好;
从方差看,七年级的方差小于八年级的方差,所以七年级的成绩比八年级的成绩稳定,七年级的成绩较好;
综上可知,七年级的比赛成绩较好一些.
24.“又是一年春光好,植树添绿正当时”,进入春季后,全国各地开始大规模开展植树造林活动,贵州各地也正在积极响应.植树节当天,某校购买了A,B两种树苗共100棵进行种植,其中A种树苗的种植单价为30元,成活率为90%,B种树苗的种植单价为37元,成活率为95%.设购买A种树苗x棵,这批树苗种植后成活y棵,请解答下列问题.
(1)求出y与x之间的函数关系式.
(2)为保证这批树苗种植后至少成活93棵,求该校用于植树造林活动的总费用的最小值.
【分析】(1)设购买A种树苗x棵,则购买B种树苗(100﹣x)棵,根据成活y棵=A种树苗成活的棵树+B种树苗成活的棵树,即可求出y与x之间的函数关系式;
(2)根据这批树苗至少成活93棵,列出关于x的不等式,可求出x的范围,再根据总费用w=购买A种树苗的费用+种植A种树苗的费用得出w与x的函数关系式,利用一次函数的性质即可求解.
解:(1)设购买A种树苗x棵,则购买B种树苗(100﹣x)棵,由题意得:
y=90%x+95%×(100﹣x)=﹣0.05x+95(0≤x≤100);
(2)由题意,可得﹣0.05x+95≥93,
解得x≤40,
设总费用为w元,
由题意,得w=30x+37×(100﹣x)=﹣7x+3700,
∵﹣7<0,
∴w随x的增大而减小,
∴当x=40时,该校用于植树造林活动的总费用最少,最小值为:﹣7×40+3700=3420(元),
答:该校用于植树造林活动的总费用的最小值为3420元.
25.操作发现:
已知正方形ABCD的边长为1,在边BC,CD上任取一点P(不与顶点B,C,D重合),连接AP,分别过点D,B作DE⊥AP于点E,BF⊥AP于点F.
(1)如图1,当点P在CD上时,求证:BF=DE+EF.
(2)如图2,当点P在CD上时,过点C作CG⊥AP交AP的延长线于点G,试判断线段DE,BF,CG间的数量关系,并说明理由.
拓广探索:
(3)如图3,当点P在BC上时,过点C作CG⊥AP交AP的延长线于点G,请直接写出线段DE,BF,CG之间的数量关系,不用写理由.
【分析】(1)由DE⊥AP,BF⊥AP,可得∠AED=∠AFB=90°,进而可证△ADE≌△BAF(AAS),再根据全等三角形性质即可证得结论;
(2)如图2,过点C作CH⊥BF于点H,同(1)可证得△DAE≌△BCH(AAS),即可得出答案;
(3)如图3.过点C作CH⊥BF交BF的延长线于点H.再由四边形ABCD为正方形,可证得△DAE≌△BCH(AAS),进而可证四边形HFGC为矩形,即可得出答案.
解:(1)如图1,∵DE⊥AP,BF⊥AP,
∴∠AED=∠AFB=90°,
∴∠DAE+∠BAF=90°,∠BAF+∠ABF=90°,
∴∠DAE=∠ABF,而AB=AD,
∴△ADE≌△BAF(AAS),
∴DE=AF,AE=BF,
∵AE=AF+EF,
∴BF=DE+EF.
(2)线段DE、BF、CG间的数量关系是BF=DE+CG.
理由如下:
如图2,过点C作CH⊥BF于点H,
∵∠CHF=∠HFG=∠CGF=90°,
∴四边形HFGC为矩形,
∴CG=FH.
同(1)可证得△DAE≌△BCH(AAS),
∴DE=BH,
∴BF=FH+BH=CG+DE.
(3)DE=BF+CG.理由如下:
如图3.过点C作CH⊥BF交BF的延长线于点H.
则∠CHB=∠AED=90°,
∵四边形ABCD为正方形,
∴AD=BC,AD∥BC,
∴∠DAE=∠BGF,
∵DE⊥AP,BF⊥AP,CG⊥AP,
∴∠AED=∠BFP=∠CGF=90°,
∴∠DAE+∠ADE=∠BPF+∠CBH=90°,
∴∠ADE=∠CBH,
∴△DAE≌△BCH(AAS),
∴DE=BH.
∵∠BHC=∠HFG=∠CGF=90°,
∴四边形HFGC为矩形,
∴HF=CG,
∵BH=BF+HF,
∴DE=BF+CG.
同课章节目录
