4.4指数函数、幂函数、对数函数增长的比较 课件(共39张PPT)-2021-2022学年高一上学期数学北师大版(2019)必修第一册
文档属性
| 名称 | 4.4指数函数、幂函数、对数函数增长的比较 课件(共39张PPT)-2021-2022学年高一上学期数学北师大版(2019)必修第一册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 7.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-09 13:41:51 | ||
图片预览








文档简介
(共39张PPT)
课件制作
胡琪
4.4指数函数、幂函数、对数函数增长的比较
北师大(2019)必修1
看看这一节我们要学什么
1.
了解三种函数的增长特征.
2.初步认识“直线上升”、“指数爆炸”和“对数增长”.
3.尝试函数模型的简单应用.
环节一
三种函数的单调性
指数函数、对数函数、幂函数单调性
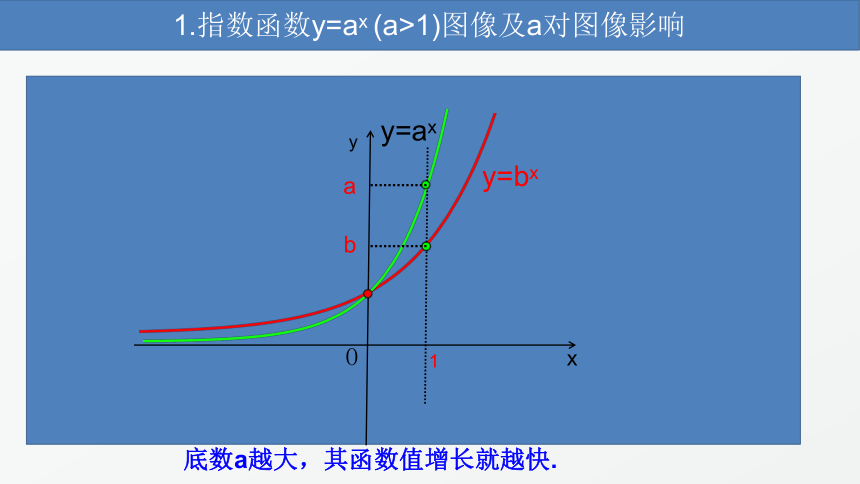
1.指数函数y=ax
(a>1),对数函数y=logax(a>1)
和幂函数y=xn
(n>0)在区间(0,+∞)上的单调性如何?
指数函数、对数函数、幂函数单调性
增函数
环节二
各自的增长特征
1.指数函数y=ax
(a>1)图像及a对图像影响
y=bx
y=ax
y
x
O
1
b
a
底数a越大,其函数值增长就越快.
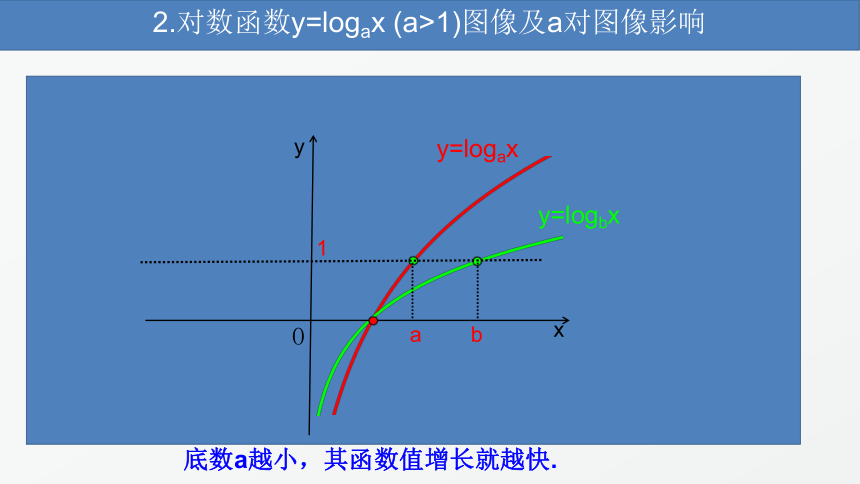
2.对数函数y=logax
(a>1)图像及a对图像影响
底数a越小,其函数值增长就越快.
y=logax
y=logbx
y
x
O
1
a
b
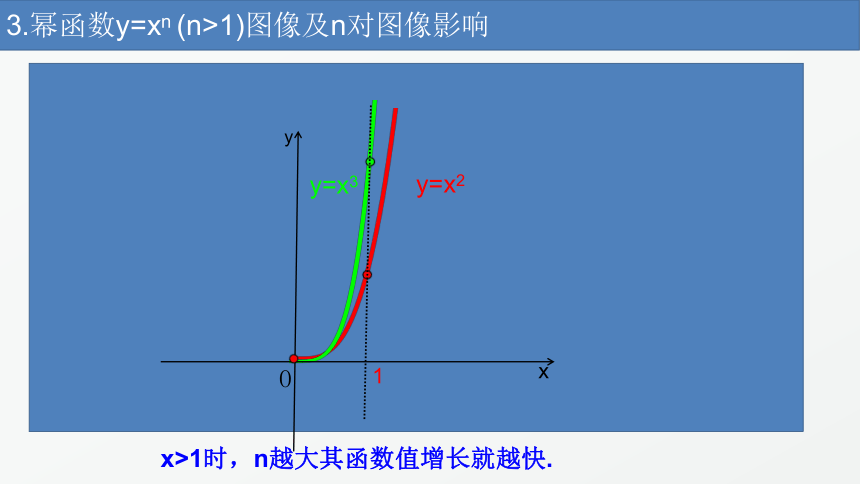
3.幂函数y=xn
(n>1)图像及n对图像影响
y=x2
y=x3
y
x
O
x>1时,n越大其函数值增长就越快.
1
环节三
增长速度比较
?
1
2
4
y=2x
y=x2
y=log2x
②在(0,2),幂函数比指数函数增长快;在(4,+∞),指数函数比幂函数增长快
①对数函数
y=log2x增长最慢
16
4
?
自变量x
函数值
y=2x
y=x100(x>0)
y=log2x
···
···
···
···
1
2
1
0
1.007
004
4
2.009
733
8
2.009
725
8
0.010
071
0
10
1
024
10100
100
1.27×1030
10200
300
2.04×1090
5.15×10247
500
3.27×10150
7.89×10269
700
5.26×10210
3.23×10284
900
8.45×10270
2.66×10295
996
6.70×10299
6.70×10299
9.960
0019
1
000
1.07×10301
10300
1
100
1.36×10331
1.38×10304
1
200
1.72×10361
8.28×10307
···
···
···
···
?
x
的
变
化
区
间
函数值的变化量
y=2x
y=x100(x>0)
y=log2x
(1,10)
1023
10100-1
3.321
928
1
(10,100)
1.27×1030
10200
3.321
928
1
(100,300)
2.04×1090
5.15×10247
(300,500)
3.27×10150
7.89×10269
(500,700)
5.26×10210
3.23×10284
(700,900)
8.45×10270
2.66×10295
(900,1000)
1.07×10301
10300
(1000,1100)
1.36×10331
1.38×10304
(1100,1200)
1.72×10361
8.28×10307
?
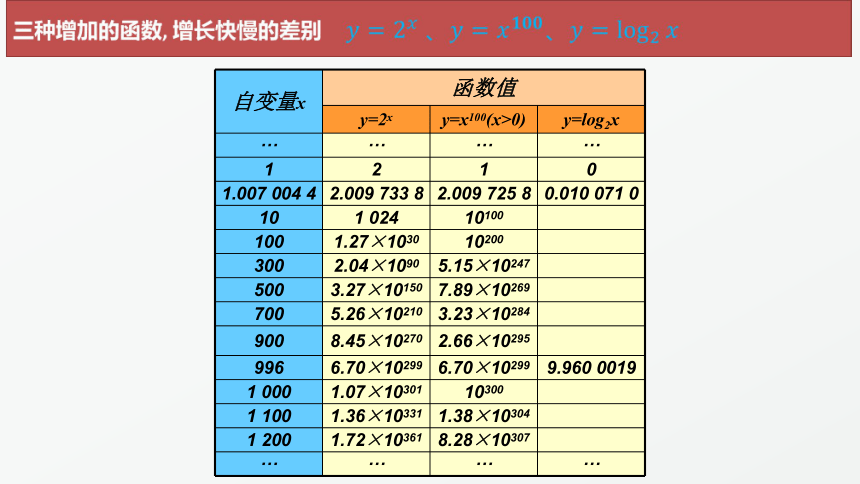
①、随着x的值越大,y=log2x的函数值增长的越来越慢,y=2x和y=x100的函数值增长的
越来越快y=log2x增长比y=2x和y=x100要慢的多。
②、对函数y=2x和y=x100而言
在x比较小时,会存在y=x100比y=2x的增长快的情况。
当x比较大时,y=2x比y=x100增长得更快。
?
x
y
y=4x
y=x4
y=log4x
4
16
o
①对数函数
y=log2x增长最慢
②在(0,2),幂函数比指数函数增长快;
在(4,+∞),指数函数比幂函数增长快
三种增加的函数,
增长快慢的差别
①对数函数增长最慢
②当自变量x大于某一个特定值时,指数函数比幂函数增长快
由于指数函数增长非常快,人们常称这种现象为“指数爆炸”。
环节四
应用
1.增长速度比较
例1(1)下列函数中,增长速度最慢的是( )
A.y=6x
B.y=log6x
C.y=x6
D.y=6x
对数函数增长的速度越来越慢,故选B
?
1.增长速度比较
?
?
1.增长速度比较
?
?
1.增长速度比较
函数f(x)的图象在区间(0,1)上递减较快,但递减速度逐渐变慢;在区间(1,+∞)上,递减较慢,且越来越慢;同样,函数g(x)的图象在区间(0,+∞)上,递减较慢,且递减速度越来越慢;函数h(x)的图象在区间(0,1)上递减较快,但递减速度变慢;在区间(1,+∞)上,递减较慢,且越来越慢.
经验一
常见函数模型及增长特点
⑴线性函数模型
y=kx+b的增长特点是直线上升,其增长速度不变.
⑵指数函数模型
y=ax随x增大,y增长速度越来越快,并且当a越大时,y=ax的函数值增长的越快.
⑶对数函数模型
y=logax随x增大,y增长速度越来越慢,并且当a越大时,y=logax的函数值增长的越慢.
2.比较大小
?
?
2.比较大小
例2
(2)已知m=0.95.1,n=5.10.9,p=log0.95.1,则这三个数的大小关系是( )
A.mB.mC.pD.p解析:∵01,p<0,∴p答案:C
2.比较大小
例2
(3)已知y1=2x,y2=x2,y3=log2x,则当2( )
A.y1>y2>y3
B.y2>y1>y3
C.y1>y3>y2
D.y2>y3>y1
解析:在同一平面直角坐标系中画出这三个函数的图象(图略),在区间(2,4)上,从上到下图象依次对应的函数为y2=x2,y1=2x,y3=log2x,故y2>y1>y3.答案:B
3.应用图像模型
例3(1)函数f(x)=2x和g(x)=x3的图象如图所示.设两函数的图象交于点A(x1,y1),B(x2,y2),且x1(1)请指出图中曲线C1,C2分别对应的函数.
(2)结合函数图象,判断f(6),g(6),f(2
017),g(2
017)的大小.
解:(1)C1对应的函数为g(x)=x3,C2对应的函数为f(x)=2x.
(2)因为f(1)>g(1),f(2)g(10),所以1017>x2.从题中图象上可以看出,当x1x2时,f(x)>g(x),所以f(2
017)>g(2
017).
又因为g(2
017)>g(6),所以f(2
017)>g(2
017)>g(6)>f(6).
3.应用图像模型
?
?
3.应用图像模型
例3(3)某林区的森林蓄积量每年比上一年平均增长10.4%,要增长到原来的x倍,需经过y年,则函数y=f(x)的图象大致是( )
设该林区的森林原有蓄积量为a,
由题意得,ax=a(1+0.104)y,故y=log1.104x(x≥1),
∴y=f(x)的图象大致为D中图象.
4.选择函数模型
例4(1)某汽车制造商在2020年初公告:公司计划2020年生产目标定为43万辆.已知该公司近三年的汽车生产量如下表所示:
年份/年
2017
2018
2019
产量/万辆
8
18
30
如果我们分别将2017,2018,2019,2020定义为第一、二、三、四年.现在有两个函数模型:一元二次函数模型f(x)=ax2+bx+c(a≠0)和指数函数模型g(x)=a·bx+c(a≠0,b>0,且b≠1),哪个模型能更好地反映该公司年产量y与年份x的关系?
4.选择函数模型
?
?
4.选择函数模型
例4(1)某汽车制造商在2020年初公告:公司计划2020年生产目标定为43万辆.已知该公司近三年的汽车生产量如下表所示:
年份/年
2017
2018
2019
产量/万辆
8
18
30
如果我们分别将2017,2018,2019,2020定义为第一、二、三、四年.现在有两个函数模型:一元二次函数模型f(x)=ax2+bx+c(a≠0)和指数函数模型g(x)=a·bx+c(a≠0,b>0,且b≠1),哪个模型能更好地反映该公司年产量y与年份x的关系?
由(1)(2)可得,函数模型f(x)=x2+7x能更好地反映该公司年产量y与年份x的关系
4.选择函数模型
例4(2)某工厂生产某种产品,每件产品的出厂价为50元,其成本为25元,在生产过程中,平均每生产一件产品有0.5
m3污水排出,为了净化环境,工厂设计两种方案进行污水处理,并准备实施.
方案1:工厂污水先净化处理后再排出,每处理1
m3污水所耗原料费为2元,并且每月排污设备损耗费为30
000元;
方案2:工厂污水排到污水厂统一处理,每处理1
m3需付14元的排污费.
(1)若工厂每月生产3
000件产品,在既不污染环境,又节约资金的前提下,应选择哪种处理污水的方案,请通过计算加以说明.
(2)若工厂每月生产6
000件产品,又该如何决策呢?
4.选择函数模型
解:设工厂每月生产x件产品,依方案1的利润为y1,依方案2的利润为y2,
则y1=(50-25)x-2×0.5x-30000=24x-30000,y2=(50-25)x-14×0.5x=18x.
(1)当x=3000时,y1=42000,y2=54000.
因为y1(2)当x=6000时,y1=114000,y2=108000.
因为y1>y2,故应选择方案1处理污水.
经验二
(1)线性函数增长模型适合于描述增长速度不变的变化规律;
(2)指数函数增长模型适合于描述增长速度急剧的变化规律;
(3)对数函数增长模型适合于描述增长速度平缓的变化规律.
因此,需抓住题中蕴含的数学信息,恰当、准确地建立相应变化
5.应用函数模型
?
?
5.应用函数模型
环节五
小结
指数爆炸中的生活哲理
三天打鱼,两天晒网
积跬步以致千里,
积怠惰以致深渊
只比你努力一点的人,
其实已经甩你很远
课件制作
胡琪
4.4指数函数、幂函数、对数函数增长的比较
北师大(2019)必修1
看看这一节我们要学什么
1.
了解三种函数的增长特征.
2.初步认识“直线上升”、“指数爆炸”和“对数增长”.
3.尝试函数模型的简单应用.
环节一
三种函数的单调性
指数函数、对数函数、幂函数单调性
1.指数函数y=ax
(a>1),对数函数y=logax(a>1)
和幂函数y=xn
(n>0)在区间(0,+∞)上的单调性如何?
指数函数、对数函数、幂函数单调性
增函数
环节二
各自的增长特征
1.指数函数y=ax
(a>1)图像及a对图像影响
y=bx
y=ax
y
x
O
1
b
a
底数a越大,其函数值增长就越快.
2.对数函数y=logax
(a>1)图像及a对图像影响
底数a越小,其函数值增长就越快.
y=logax
y=logbx
y
x
O
1
a
b
3.幂函数y=xn
(n>1)图像及n对图像影响
y=x2
y=x3
y
x
O
x>1时,n越大其函数值增长就越快.
1
环节三
增长速度比较
?
1
2
4
y=2x
y=x2
y=log2x
②在(0,2),幂函数比指数函数增长快;在(4,+∞),指数函数比幂函数增长快
①对数函数
y=log2x增长最慢
16
4
?
自变量x
函数值
y=2x
y=x100(x>0)
y=log2x
···
···
···
···
1
2
1
0
1.007
004
4
2.009
733
8
2.009
725
8
0.010
071
0
10
1
024
10100
100
1.27×1030
10200
300
2.04×1090
5.15×10247
500
3.27×10150
7.89×10269
700
5.26×10210
3.23×10284
900
8.45×10270
2.66×10295
996
6.70×10299
6.70×10299
9.960
0019
1
000
1.07×10301
10300
1
100
1.36×10331
1.38×10304
1
200
1.72×10361
8.28×10307
···
···
···
···
?
x
的
变
化
区
间
函数值的变化量
y=2x
y=x100(x>0)
y=log2x
(1,10)
1023
10100-1
3.321
928
1
(10,100)
1.27×1030
10200
3.321
928
1
(100,300)
2.04×1090
5.15×10247
(300,500)
3.27×10150
7.89×10269
(500,700)
5.26×10210
3.23×10284
(700,900)
8.45×10270
2.66×10295
(900,1000)
1.07×10301
10300
(1000,1100)
1.36×10331
1.38×10304
(1100,1200)
1.72×10361
8.28×10307
?
①、随着x的值越大,y=log2x的函数值增长的越来越慢,y=2x和y=x100的函数值增长的
越来越快y=log2x增长比y=2x和y=x100要慢的多。
②、对函数y=2x和y=x100而言
在x比较小时,会存在y=x100比y=2x的增长快的情况。
当x比较大时,y=2x比y=x100增长得更快。
?
x
y
y=4x
y=x4
y=log4x
4
16
o
①对数函数
y=log2x增长最慢
②在(0,2),幂函数比指数函数增长快;
在(4,+∞),指数函数比幂函数增长快
三种增加的函数,
增长快慢的差别
①对数函数增长最慢
②当自变量x大于某一个特定值时,指数函数比幂函数增长快
由于指数函数增长非常快,人们常称这种现象为“指数爆炸”。
环节四
应用
1.增长速度比较
例1(1)下列函数中,增长速度最慢的是( )
A.y=6x
B.y=log6x
C.y=x6
D.y=6x
对数函数增长的速度越来越慢,故选B
?
1.增长速度比较
?
?
1.增长速度比较
?
?
1.增长速度比较
函数f(x)的图象在区间(0,1)上递减较快,但递减速度逐渐变慢;在区间(1,+∞)上,递减较慢,且越来越慢;同样,函数g(x)的图象在区间(0,+∞)上,递减较慢,且递减速度越来越慢;函数h(x)的图象在区间(0,1)上递减较快,但递减速度变慢;在区间(1,+∞)上,递减较慢,且越来越慢.
经验一
常见函数模型及增长特点
⑴线性函数模型
y=kx+b的增长特点是直线上升,其增长速度不变.
⑵指数函数模型
y=ax随x增大,y增长速度越来越快,并且当a越大时,y=ax的函数值增长的越快.
⑶对数函数模型
y=logax随x增大,y增长速度越来越慢,并且当a越大时,y=logax的函数值增长的越慢.
2.比较大小
?
?
2.比较大小
例2
(2)已知m=0.95.1,n=5.10.9,p=log0.95.1,则这三个数的大小关系是( )
A.m
2.比较大小
例2
(3)已知y1=2x,y2=x2,y3=log2x,则当2
A.y1>y2>y3
B.y2>y1>y3
C.y1>y3>y2
D.y2>y3>y1
解析:在同一平面直角坐标系中画出这三个函数的图象(图略),在区间(2,4)上,从上到下图象依次对应的函数为y2=x2,y1=2x,y3=log2x,故y2>y1>y3.答案:B
3.应用图像模型
例3(1)函数f(x)=2x和g(x)=x3的图象如图所示.设两函数的图象交于点A(x1,y1),B(x2,y2),且x1
(2)结合函数图象,判断f(6),g(6),f(2
017),g(2
017)的大小.
解:(1)C1对应的函数为g(x)=x3,C2对应的函数为f(x)=2x.
(2)因为f(1)>g(1),f(2)
017)>g(2
017).
又因为g(2
017)>g(6),所以f(2
017)>g(2
017)>g(6)>f(6).
3.应用图像模型
?
?
3.应用图像模型
例3(3)某林区的森林蓄积量每年比上一年平均增长10.4%,要增长到原来的x倍,需经过y年,则函数y=f(x)的图象大致是( )
设该林区的森林原有蓄积量为a,
由题意得,ax=a(1+0.104)y,故y=log1.104x(x≥1),
∴y=f(x)的图象大致为D中图象.
4.选择函数模型
例4(1)某汽车制造商在2020年初公告:公司计划2020年生产目标定为43万辆.已知该公司近三年的汽车生产量如下表所示:
年份/年
2017
2018
2019
产量/万辆
8
18
30
如果我们分别将2017,2018,2019,2020定义为第一、二、三、四年.现在有两个函数模型:一元二次函数模型f(x)=ax2+bx+c(a≠0)和指数函数模型g(x)=a·bx+c(a≠0,b>0,且b≠1),哪个模型能更好地反映该公司年产量y与年份x的关系?
4.选择函数模型
?
?
4.选择函数模型
例4(1)某汽车制造商在2020年初公告:公司计划2020年生产目标定为43万辆.已知该公司近三年的汽车生产量如下表所示:
年份/年
2017
2018
2019
产量/万辆
8
18
30
如果我们分别将2017,2018,2019,2020定义为第一、二、三、四年.现在有两个函数模型:一元二次函数模型f(x)=ax2+bx+c(a≠0)和指数函数模型g(x)=a·bx+c(a≠0,b>0,且b≠1),哪个模型能更好地反映该公司年产量y与年份x的关系?
由(1)(2)可得,函数模型f(x)=x2+7x能更好地反映该公司年产量y与年份x的关系
4.选择函数模型
例4(2)某工厂生产某种产品,每件产品的出厂价为50元,其成本为25元,在生产过程中,平均每生产一件产品有0.5
m3污水排出,为了净化环境,工厂设计两种方案进行污水处理,并准备实施.
方案1:工厂污水先净化处理后再排出,每处理1
m3污水所耗原料费为2元,并且每月排污设备损耗费为30
000元;
方案2:工厂污水排到污水厂统一处理,每处理1
m3需付14元的排污费.
(1)若工厂每月生产3
000件产品,在既不污染环境,又节约资金的前提下,应选择哪种处理污水的方案,请通过计算加以说明.
(2)若工厂每月生产6
000件产品,又该如何决策呢?
4.选择函数模型
解:设工厂每月生产x件产品,依方案1的利润为y1,依方案2的利润为y2,
则y1=(50-25)x-2×0.5x-30000=24x-30000,y2=(50-25)x-14×0.5x=18x.
(1)当x=3000时,y1=42000,y2=54000.
因为y1
因为y1>y2,故应选择方案1处理污水.
经验二
(1)线性函数增长模型适合于描述增长速度不变的变化规律;
(2)指数函数增长模型适合于描述增长速度急剧的变化规律;
(3)对数函数增长模型适合于描述增长速度平缓的变化规律.
因此,需抓住题中蕴含的数学信息,恰当、准确地建立相应变化
5.应用函数模型
?
?
5.应用函数模型
环节五
小结
指数爆炸中的生活哲理
三天打鱼,两天晒网
积跬步以致千里,
积怠惰以致深渊
只比你努力一点的人,
其实已经甩你很远
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
