第二章 匀变速直线运动的研究 基础达标—2021-2022学年高一上学期物理人教版(word版含答案)必修第一册
文档属性
| 名称 | 第二章 匀变速直线运动的研究 基础达标—2021-2022学年高一上学期物理人教版(word版含答案)必修第一册 |

|
|
| 格式 | docx | ||
| 文件大小 | 376.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-08-09 00:00:00 | ||
图片预览




文档简介
高一物理人教版(2019)必修一第二章基础达标
一、单选题(共10题)
1.甲、乙、丙三个质点按如图所示的规律在同一直线上运动,其中丙质点的位移一时间图像是顶点过坐标原点的抛物线,则下列说法中正确的是( )
A.?丙质点做匀加速直线运动
B.?甲、乙两个质点运动方向相同
C.?
时甲、乙两质点距离最近
D.?甲质点做匀加速直线运动
2.为了制止高楼住户向窗外随意丢弃垃圾的陋习,某同学在自家(二楼)窗子上、下边框安装光电探测装置,利用自由落体运动规律推断丢弃垃圾住户的楼层。重力加速度g取10m/s2
,
每层楼高3米左右,设他家窗子上、下边框之间的距离为0.9m。某天光电探测装置检测到一下落物件经过该窗口的时间为0.03s,假设丢物住户是从窗口将物件从静止丢下的。估计丢物住户的楼层是(??
)
A.?14楼????????????????????????????????????B.?17楼????????????????????????????????????C.?20楼????????????????????????????????????D.?23楼
3.如图所示为一质点运动的位移-时间图像,曲线为一段圆弧,则下列说法中正确的是(??
)
A.?质点做曲线运动??????????????????????????????????????????????????B.?质点可能做匀速圆周运动
C.?质点在t1时刻离开出发点最远?????????????????????????????D.?质点运动的速率先减小后增大
4.亚丁湾索马里海域六艘海盗快艇试图靠近中国海军护航编队保护的商船,中国特战队员发射爆震弹成功将其驱离。假如其中一艘海盗快艇在海面上运动的v?t图像如图所示,设运动过程中海盗快艇所受阻力不变,则下列说法正确的是(??
)
A.?海盗快艇在0~66s内从静止出发做曲线运动???????B.?海盗快艇在96s末开始调头逃离
C.?海盗快艇在66s末离商船最近??????????????????????????????D.?海盗快艇在96~116s内做匀减速直线运动
5.甲、乙两质点做直线运动的x-t图像如图所示,其中甲图线为曲线,乙图线为直线,
s时,两图线相切,下列说法不正确的是(??
)
A.?
s时,甲、乙两质点速度均为3m/s???????????B.?
s时,甲、乙两质点没有相遇
C.?0~2.5s,甲的平均速度为4m/s???????????????????????????D.?在
s时,乙的纵坐标
m
6.CBA(中国男子篮球职业联赛)篮球筐距地面高度3.05m,某篮球运动员站立举手能达到高度2.53m。如图所示,他竖直跳起将篮球扣入栏中,重力加速度
,他起跳的初速度约为(??
)
A.?1m/s?????????????????????????????????B.?2.5m/s?????????????????????????????????C.?3.8m/s?????????????????????????????????D.?10m/s
7.一辆汽车以
的速度在平直公路上匀速行驶,因故突然紧急刹车,随后汽车停了下来。刹车时做匀减速运动的加速度大小为
,则(??
)
A.?刹车时汽车做匀减速运动的总时间为
??B.?刹车时汽车在
末的速度大小为
C.?刹车时汽车在前
内通过的位移为
???D.?刹车时汽车通过的总位移为
8.甲、乙两物体先后从同一地点出发,沿一条直线运动,它们的
图像如图所示,由图可知(??
)
A.?乙物体
末开始做加速运动,加速度大小为
B.?
时,乙物体追上了甲物体
C.?乙物体在前
内通过的位移为
D.?
时,甲在乙前面,它们之间的距离为乙追上甲前的最大距离
9.衢宁铁路于2020年9月27日开通运营,如图有一列车调度员在第1节车厢前端等待发车,列车启动后第3节车厢通过他用时
。已知每节车厢长为
,动车出站可视为匀加速直线运动,则该动车的加速度大小约为(??
)
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?
10.甲、乙两小车在同一地点同时开始往相同方向做直线运动的v-t图像如图所示(甲小车速度减为0后不再运动),根据图像提供的信息可知(?
)
A.?甲车在0-4s内的加速度大小为2m/s2??????????????????B.?甲车0-4s内与4-6s内的速度方向相反
C.?在乙追上甲之前,4s末两小车相距最远??????????????D.?8s末甲、乙两小车相遇,且离出发点距离为32m
二、多选题(共7题)
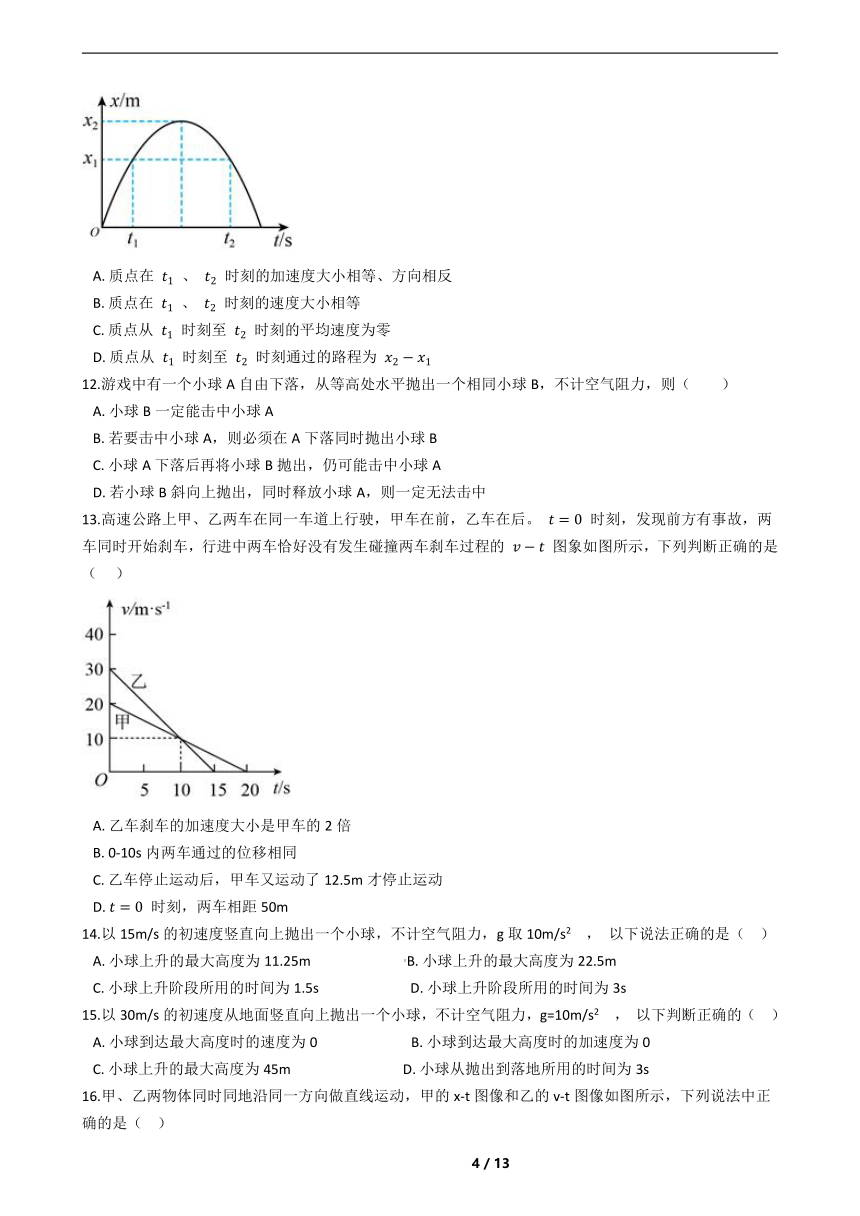
11.如图,某一质点做直线运动的
图像是抛物线的一部分,下列说法正确的是( )
A.?质点在
、
时刻的加速度大小相等、方向相反
B.?质点在
、
时刻的速度大小相等
C.?质点从
时刻至
时刻的平均速度为零
D.?质点从
时刻至
时刻通过的路程为
12.游戏中有一个小球A自由下落,从等高处水平抛出一个相同小球B,不计空气阻力,则( )
A.?小球B一定能击中小球A
B.?若要击中小球A,则必须在A下落同时抛出小球B
C.?小球A下落后再将小球B抛出,仍可能击中小球A
D.?若小球B斜向上抛出,同时释放小球A,则一定无法击中
13.高速公路上甲、乙两车在同一车道上行驶,甲车在前,乙车在后。
时刻,发现前方有事故,两车同时开始刹车,行进中两车恰好没有发生碰撞两车刹车过程的
图象如图所示,下列判断正确的是(???
)
A.?乙车刹车的加速度大小是甲车的2倍
B.?0-10s内两车通过的位移相同
C.?乙车停止运动后,甲车又运动了12.5m才停止运动
D.?
时刻,两车相距50m
14.以15m/s的初速度竖直向上抛出一个小球,不计空气阻力,g取10m/s2
,
以下说法正确的是(??
)
A.?小球上升的最大高度为11.25m???????????????????????????B.?小球上升的最大高度为22.5m
C.?小球上升阶段所用的时间为1.5s??????????????????????????D.?小球上升阶段所用的时间为3s
15.以30m/s的初速度从地面竖直向上抛出一个小球,不计空气阻力,g=10m/s2
,
以下判断正确的(??
)
A.?小球到达最大高度时的速度为0???????????????????????????B.?小球到达最大高度时的加速度为0
C.?小球上升的最大高度为45m????????????????????????????????D.?小球从抛出到落地所用的时间为3s
16.甲、乙两物体同时同地沿同一方向做直线运动,甲的x-t图像和乙的v-t图像如图所示,下列说法中正确的是(??
)
A.?0~2s内,甲、乙两物体之间的距离一直增大???????B.?第3s内,甲、乙两物体速度方向相反
C.?2~4s内,甲、乙均做减速运动????????????????????????????D.?6s末,甲、乙两物体均回到原出发点
17.在一次救灾活动中,一辆救灾汽车由静止开始做匀变速直线运动,刚运动了10s,由于前方突然有巨石滚下,堵在路中央,所以又紧急刹车,匀减速运动经5s停在巨石前。则关于汽车的运动情况,下列说法正确的是(??
)
A.?加速、减速中的加速度大小之比
?????B.?加速、减速中的平均速度大小之比
C.?加速、减速中的位移之比
????????????????D.?加速、减速中的平均速度大小之比
三、综合题(共3题)
18.如图是中国人民解放军的一次低空跳伞演练,假设伞兵离开悬停在空中的飞机后做自由落体运动,
末打开降落伞,此时速度为
,打开伞后伞兵以
的加速度竖直向下做匀减速运动,伞兵落地时速度恰好为
。求:
(1)伞兵打开伞时的速度大小
(2)伞兵打开伞时的离地高度
19.在疫情期间,智能送餐机器人可以尽量减少人员的接触,图为某款智能送餐机器人。某次机器人给
远处的顾客送菜,机器人从静止开始加速,
后速度达到
,然后做匀速直线运动,距离顾客
时开始减速,到达顾客身边恰能停止,机器人加速、减速阶段均可视为匀变速直线运动。求机器人:
(1)匀加速阶段的加速度大小;
(2)匀减速阶段的时间;
(3)整个送餐过程的平均速度大小。
20.甲、乙两车相距16.5m且甲在前乙在后,它们同时向同一方向运动,其中甲以15m/s的速度匀速行驶,乙以3m/s2的加速度由静止开始做匀加速直线运动,求
(1)甲、乙两车何时相距最远,最远距离多大?
(2)乙车何时能赶上甲车,此时乙车的速度是多大?
答案解析部分
一、单选题
1.【答案】
A
【解析】【解答】A.对比初速度为零的匀加速直线位移公式
可知,丙质点做匀加速直线运动,A符合题意;
BD.甲朝正方向做匀速直线运动,乙朝负方向做匀速直线运动,故甲、乙两个质点运动方向不同,BD不符合题意;
C.
时甲、乙两质点距离最远,C不符合题意。
故答案为:A。
【分析】根据运动图像画出两个物体的运动简图,由运动学公式列方程求解。
2.【答案】
B
【解析】【解答】设窗户上沿到物体下落点的距离为h,下落时间为t1
,
则有
到窗户下沿则有
联立可得
楼层数约为
因为该同学家在二楼,所以估计丢物住户的楼层是17楼.
故答案为:B。
【分析】利用自由落体的位移公式可以求出楼层的高度,结合每层楼的高度可以求出楼层的层数。
3.【答案】
D
【解析】【解答】AB.根据斜率等于速度可知,质点的速度先沿正方向,后沿负方向,质点一定做直线运动。AB不符合题意;
C.在t1时刻质点的位移为零,表示质点在t1时刻回到出发点,C不符合题意;
D.由斜率看出,质点的速度先减小后增大,D符合题意。
故答案为:D。
【分析】位移的图象只规定了两个方向所以质点做直线运动;利用图象斜率可以判别速度的变化;利用坐标可以判别其位移的大小。
4.【答案】
B
【解析】【解答】A.根据v-t图象的意义可知,某点处切线的斜率表示该点处的加速度,由题图可知,0~66?s内快艇做加速度逐渐减小的加速直线运动,A不符合题意;
BC.66s时快艇开始减速,96s时减速到零,此时离商船最近,然后开始调头,B符合题意,C不符合题意;
D.96~116s内,加速度为负且为定值,说明快艇反方向做匀加速直线运动,D不符合题意。
故答案为:B。
【分析】v-t图像的斜率大小表示速度大小,正负表示速度方向,图像与坐标轴围城的面积表示这段时间内的位移,即可求解。
5.【答案】
B
【解析】【解答】A.t=1.8s时,甲、乙两质点速度均为
A正确,不合题意;
B.t=1.8s时,甲、乙两质点位置相同,二者相遇,B错误,符合题意;
C.0~2.5s,甲的平均速度和平均速率均为
C正确,不合题意;
D.根据
可得在2.5s时刻,乙的纵坐标x=1.7×3m=5.1m,D正确,不合题意。
故答案为:B。
【分析】利用初末位置坐标及运动的时间可以求出两质点的速度大小;利用交点可以判别两个物体相遇;利用位移和时间可以求出平均速度的大小;利用乙的速度可以求出其末坐标的大小。
6.【答案】
C
【解析】【解答】根据v2=2gh可得
因运动员竖直跳起将篮球扣入栏中,可知起跳的略大于3.2m/s;
故答案为:C。
【分析】运动员做竖直上抛运动,利用速度位移公式可以求出起跳速度的大小。
7.【答案】
C
【解析】【解答】A.刹车时汽车做匀减速运动的总时间为
A不符合题意;
B.刹车时汽车在5s末汽车已经停止,则6s末的速度大小为0,B不符合题意;
C.刹车时汽车在前
内通过的位移为
C符合题意;
D.刹车时汽车通过的总位移为
D不符合题意。
故答案为:C。
【分析】运用匀变速运动的速度公式可以求得时间,汽车刹车计算速度时要注意刹车停止的时间,运用匀变速的位移公式求位移即可。
8.【答案】
D
【解析】【解答】A.乙物体
末开始做加速运动,加速度大小为
A不符合题意;
B.根据图像和时间轴围成的面积表示位移,则
时,甲乙位移不同,甲、乙两物体从同一地点出发,则乙物体没有追上甲物体,B不符合题意;
C.根据图像和时间轴围成的面积表示位移,乙物体在前
内通过的位移
C不符合题意;
D.在10~20s内,甲的速度大于乙的速度,甲比乙运动得快,甲在乙的前方,两者距离逐渐增大;20s后,乙的速度大于甲的速度,乙比甲运动得快,两者距离逐渐减小,在t=20s时刻两者距离最大,D符合题意。
故答案为:D。
【分析】速度图象反映物体速度随时间的变化情况,可直接读出速度的大小;速度图象的“面积”大
小等于物体通过的位移大小,根据位移关系即可分析乙何时追上甲;根据速度的大小关系,判断两者距离的变化.
9.【答案】
A
【解析】【解答】根据
可得第3节车厢经过他的时间为
解得
故答案为:A。
【分析】利用匀变速直线运动的位移公式结合其三节车厢运动时间和两节车厢运动时间的差值可以求出加速度的大小。
10.【答案】
D
【解析】【解答】A.由图可知,甲车在0-4s内的加速度大小为1m/s2
,
A不符合题意;
B.甲车0-4s内与4-6s内的速度方向相同,B不符合题意;
C.由图4-6s内甲车的加速度为-4m/s2
,
甲车从4s末经过
与乙车速度相等。
所以从运动开始经过5s甲乙两车速度相等,在5s之前甲车速度大于乙车,甲乙之间的距离越来越大,5s之后甲车速度小于乙车,甲乙之间的距离越来越小,所以在乙追上甲之前,5s末两小车相距最远,C不符合题意;
D.根据图像,可知甲车在0-8s内的位移
乙车在0-8s内的位移
所以8s末甲、乙两小车相遇,且离出发点距离为32m,D符合题意。
故答案为:D。
【分析】利用图像斜率可以求出加速度的大小;利用速度的符号可以判别速度的方向;两车其速度相等时其距离最大;利用面积的大小可以求出汽车的位移。
二、多选题
11.【答案】
B,C
【解析】【解答】A.质点做直线运动的
图像是抛物线的一部分,说明质点做的是匀变速直线运动,A不符合题意;
B.根据抛物线的特点,图线在
、
时刻的斜率大小相等,故质点在
、
时刻的速度大小相等,B符合题意;
C.质点从
时刻至
时刻通过的位移为零,可知质点在这段时间内的平均速度为零,C符合题意;
D.从
时刻至
时刻,质点先由
向
位置运动,再由
向
位置运动,通过的路程为
,D不符合题意。
故答案为:BC。
【分析】利用图线为抛物线所以可以判别质点做匀变速直线运动其加速度保持不变;利用图像斜率可以判别速度的大小;利用初末位置可以求出位移的大小,除以对应时间可以求出平均速度的大小;利用质点的位置可以求出通过的路程的大小。
12.【答案】
B,D
【解析】【解答】ABC.小球A自由下落,小球B从等高处水平抛出,要想击中A球,必须两个小球下落的高度相等,小球B在竖直方向做自由落体运动,所以必须同时抛出才能击中,AC不符合题意B符合题意;
D.小球B斜向上抛出,小球B在竖直方向上做竖直上抛运动,A小球做自由落体运动,不能击中,D符合题意。
故答案为:BD。
【分析】根据自由落体运动与抛体运动的规律结合运动学公式列方程求解。
13.【答案】
A,C,D
【解析】【解答】A.根据v-t图像的斜率表示加速度,知甲的加速度大小为
乙车的加速度大小为
故乙车的加速度大小是甲车的2倍,
A符合题意;
B.由v-t图像与时间轴所围成的面积表示物体发生的位移,可判断0~10s时两车通过的位移不相同,且乙车发生的位移大于甲车发生的位移,B不符合题意;
C.乙车在t=15s时停止运动,此时甲的速度为
,乙车停止运动后,甲车又运动了
C符合题意;
D.若行进中两车恰好没有发生碰撞,说明t=10s时刻两车速度相等时恰好相遇,则t=0时刻两车间距等于两车等于在0-10s内位移之差,如图中虚线面积
D符合题意。
故答案为:ACD。
【分析】利用图像斜率可以求出加速度的大小;利用图像面积可以求出位移的大小;利用图像面积可以求出运动的位移;利用共速时两车相遇结合面积可以求出最初两车相距的距离。
14.【答案】
A,C
【解析】【解答】AB.竖直上抛的小球,不计阻力时只受到自身重力作用,为匀减速,加速度
,上升到最高点时,速度为0。根据匀变速直线运动有
得到
A符合题意,B不符合题意;
CD.上升过程运动时间
C符合题意,D不符合题意。
故答案为:AC。
【分析】利用竖直上抛运动的速度位移公式可以求出上升的最大高度,结合速度公式可以求出运动的时间。
15.【答案】
A,C
【解析】【解答】AB.竖直上抛的小球,不计阻力时只受到自身重力作用,为匀减速,加速度
,小球上升到最高点时,速度为0,最高点时依然受重力作用,加速度
,A符合题意,B不符合题意;
C.上升过程根据匀变速直线运动规律有
解得
C符合题意;
D.上升过程运动时间
则小球从抛出到落地所用的时间为6s,D不符合题意。
故答案为:AC。
【分析】小球到达最高点时速度等于0其加速度等于重力加速度;利用速度位移公式可以求出最大的高度;利用速度公式可以求出运动的时间。
16.【答案】
B,D
【解析】【解答】A.根据x-t图象的斜率表示速度,知0~2s内甲物体沿正向做速度为2m/s的匀速直线运动,乙沿正向做初速度为0的匀加速直线运动,甲的速度先大于乙的速度,后小于乙的速度,则知甲、乙两物体之间的距离先增大后减小,A不符合题意;
B.根据x-t图象的斜率表示速度,知第3秒内甲的速度为负。由v-t图象知第3秒内乙物体速度为正,则第3秒内甲、乙两物体速度方向相反,B符合题意;
C.2~4s内,甲做负方向的匀速直线运动,乙2~3s做正方向匀减速直线运动,3~4s做负方向匀加速直线运动,C不符合题意;
D.6s末,甲的位移为零,v-t与时间轴所围的“面积”表示位移,知t=6s时,乙的位移为零,故6s末,甲、乙两物体均回到原出发点,D符合题意。
故答案为:BD。
【分析】利用位移时间图像的斜率可以判别甲车的速度,利用两车的速度比较可以判别两车距离的变化;利用位移图像斜率可以判别速度的方向,利用速度方向可以判别速度的方向;利用图像斜率可以判别甲的速度变化;利用位移时间图像的坐标可以判别甲的位移;利用速度时间图像的面积可以判别乙的位移。
17.【答案】
B,C
【解析】【解答】A.设加速的末速度为v,则有
加速、减速中的加速度大小之比
A不符合题意;
BD.根据匀变速直线运动的平均速度公式
得,加速、减速中的平均速度大小之比
B符合题意,D不符合题意;
C.根据位移公式
得,加速、减速中的位移之比
C符合题意。
故答案为:BC。
【分析】利用速度公式可以求出加速和减速的加速度比值;利用初末速度之和的一半可以求出平均速度的比值;利用平均速度结合运动时间可以求出位移的比值。
三、综合题
18.【答案】
(1)由自由落体速度公式可得
解得伞兵打开伞时的速度大小为
(2)打开伞后下落过程,由位移公式可得
解得伞兵打开伞时的离地高度为
【解析】【分析】(1)根据自由落体运动的速度公式列方程求解。
(2)由下落过程中速度与位移的关系列方程求解。
19.【答案】
(1)解:在加速过程由
可得
(2)解:在减速过程由
可得
(3)解:在加速度过程由
可得
则匀速过程
得
则全程的平均速度大小由
可得
【解析】【分析】(1)机器人做匀加速直线运动,利用加速度的定义式可以求出加速度的大小;
(2)机器人做匀减速直线运动,利用平均速度公式可以求出运动的时间;
(3)在加速过程中,利用平均速度公式可以求出机器人的位移,利用匀速运动的位移公式可以求出机器人匀速运动过程的时间,利用全程的位移和全程的运动时间可以求出平均速度的大小。
?
?
20.【答案】
(1)解:当两车的速度相等时,相距最远v1=at1
可得
甲车运动的距离
乙车运动的距离
此时相距的最远距离
(2)解:设经过t时间乙车追上甲车,有
代入数据解得t=11s
此时乙车的速度v2=at=3×11m/s=33m/s
【解析】【分析】(1)当两车速度相等时两车距离最远,乙车做匀加速直线运动,甲车做匀速直线运动,利用速度公式可以求出乙车加速的时间,结合两车的位移公式可以求出两车之间的距离;
(2)经过一段时间后乙车追上甲车,利用位移相等结合两车的位移公式可以求出相遇的时间,利用乙车的速度公式可以求出乙车速度的大小。
1
/
3
一、单选题(共10题)
1.甲、乙、丙三个质点按如图所示的规律在同一直线上运动,其中丙质点的位移一时间图像是顶点过坐标原点的抛物线,则下列说法中正确的是( )
A.?丙质点做匀加速直线运动
B.?甲、乙两个质点运动方向相同
C.?
时甲、乙两质点距离最近
D.?甲质点做匀加速直线运动
2.为了制止高楼住户向窗外随意丢弃垃圾的陋习,某同学在自家(二楼)窗子上、下边框安装光电探测装置,利用自由落体运动规律推断丢弃垃圾住户的楼层。重力加速度g取10m/s2
,
每层楼高3米左右,设他家窗子上、下边框之间的距离为0.9m。某天光电探测装置检测到一下落物件经过该窗口的时间为0.03s,假设丢物住户是从窗口将物件从静止丢下的。估计丢物住户的楼层是(??
)
A.?14楼????????????????????????????????????B.?17楼????????????????????????????????????C.?20楼????????????????????????????????????D.?23楼
3.如图所示为一质点运动的位移-时间图像,曲线为一段圆弧,则下列说法中正确的是(??
)
A.?质点做曲线运动??????????????????????????????????????????????????B.?质点可能做匀速圆周运动
C.?质点在t1时刻离开出发点最远?????????????????????????????D.?质点运动的速率先减小后增大
4.亚丁湾索马里海域六艘海盗快艇试图靠近中国海军护航编队保护的商船,中国特战队员发射爆震弹成功将其驱离。假如其中一艘海盗快艇在海面上运动的v?t图像如图所示,设运动过程中海盗快艇所受阻力不变,则下列说法正确的是(??
)
A.?海盗快艇在0~66s内从静止出发做曲线运动???????B.?海盗快艇在96s末开始调头逃离
C.?海盗快艇在66s末离商船最近??????????????????????????????D.?海盗快艇在96~116s内做匀减速直线运动
5.甲、乙两质点做直线运动的x-t图像如图所示,其中甲图线为曲线,乙图线为直线,
s时,两图线相切,下列说法不正确的是(??
)
A.?
s时,甲、乙两质点速度均为3m/s???????????B.?
s时,甲、乙两质点没有相遇
C.?0~2.5s,甲的平均速度为4m/s???????????????????????????D.?在
s时,乙的纵坐标
m
6.CBA(中国男子篮球职业联赛)篮球筐距地面高度3.05m,某篮球运动员站立举手能达到高度2.53m。如图所示,他竖直跳起将篮球扣入栏中,重力加速度
,他起跳的初速度约为(??
)
A.?1m/s?????????????????????????????????B.?2.5m/s?????????????????????????????????C.?3.8m/s?????????????????????????????????D.?10m/s
7.一辆汽车以
的速度在平直公路上匀速行驶,因故突然紧急刹车,随后汽车停了下来。刹车时做匀减速运动的加速度大小为
,则(??
)
A.?刹车时汽车做匀减速运动的总时间为
??B.?刹车时汽车在
末的速度大小为
C.?刹车时汽车在前
内通过的位移为
???D.?刹车时汽车通过的总位移为
8.甲、乙两物体先后从同一地点出发,沿一条直线运动,它们的
图像如图所示,由图可知(??
)
A.?乙物体
末开始做加速运动,加速度大小为
B.?
时,乙物体追上了甲物体
C.?乙物体在前
内通过的位移为
D.?
时,甲在乙前面,它们之间的距离为乙追上甲前的最大距离
9.衢宁铁路于2020年9月27日开通运营,如图有一列车调度员在第1节车厢前端等待发车,列车启动后第3节车厢通过他用时
。已知每节车厢长为
,动车出站可视为匀加速直线运动,则该动车的加速度大小约为(??
)
A.????????????????????????????????B.????????????????????????????????C.????????????????????????????????D.?
10.甲、乙两小车在同一地点同时开始往相同方向做直线运动的v-t图像如图所示(甲小车速度减为0后不再运动),根据图像提供的信息可知(?
)
A.?甲车在0-4s内的加速度大小为2m/s2??????????????????B.?甲车0-4s内与4-6s内的速度方向相反
C.?在乙追上甲之前,4s末两小车相距最远??????????????D.?8s末甲、乙两小车相遇,且离出发点距离为32m
二、多选题(共7题)
11.如图,某一质点做直线运动的
图像是抛物线的一部分,下列说法正确的是( )
A.?质点在
、
时刻的加速度大小相等、方向相反
B.?质点在
、
时刻的速度大小相等
C.?质点从
时刻至
时刻的平均速度为零
D.?质点从
时刻至
时刻通过的路程为
12.游戏中有一个小球A自由下落,从等高处水平抛出一个相同小球B,不计空气阻力,则( )
A.?小球B一定能击中小球A
B.?若要击中小球A,则必须在A下落同时抛出小球B
C.?小球A下落后再将小球B抛出,仍可能击中小球A
D.?若小球B斜向上抛出,同时释放小球A,则一定无法击中
13.高速公路上甲、乙两车在同一车道上行驶,甲车在前,乙车在后。
时刻,发现前方有事故,两车同时开始刹车,行进中两车恰好没有发生碰撞两车刹车过程的
图象如图所示,下列判断正确的是(???
)
A.?乙车刹车的加速度大小是甲车的2倍
B.?0-10s内两车通过的位移相同
C.?乙车停止运动后,甲车又运动了12.5m才停止运动
D.?
时刻,两车相距50m
14.以15m/s的初速度竖直向上抛出一个小球,不计空气阻力,g取10m/s2
,
以下说法正确的是(??
)
A.?小球上升的最大高度为11.25m???????????????????????????B.?小球上升的最大高度为22.5m
C.?小球上升阶段所用的时间为1.5s??????????????????????????D.?小球上升阶段所用的时间为3s
15.以30m/s的初速度从地面竖直向上抛出一个小球,不计空气阻力,g=10m/s2
,
以下判断正确的(??
)
A.?小球到达最大高度时的速度为0???????????????????????????B.?小球到达最大高度时的加速度为0
C.?小球上升的最大高度为45m????????????????????????????????D.?小球从抛出到落地所用的时间为3s
16.甲、乙两物体同时同地沿同一方向做直线运动,甲的x-t图像和乙的v-t图像如图所示,下列说法中正确的是(??
)
A.?0~2s内,甲、乙两物体之间的距离一直增大???????B.?第3s内,甲、乙两物体速度方向相反
C.?2~4s内,甲、乙均做减速运动????????????????????????????D.?6s末,甲、乙两物体均回到原出发点
17.在一次救灾活动中,一辆救灾汽车由静止开始做匀变速直线运动,刚运动了10s,由于前方突然有巨石滚下,堵在路中央,所以又紧急刹车,匀减速运动经5s停在巨石前。则关于汽车的运动情况,下列说法正确的是(??
)
A.?加速、减速中的加速度大小之比
?????B.?加速、减速中的平均速度大小之比
C.?加速、减速中的位移之比
????????????????D.?加速、减速中的平均速度大小之比
三、综合题(共3题)
18.如图是中国人民解放军的一次低空跳伞演练,假设伞兵离开悬停在空中的飞机后做自由落体运动,
末打开降落伞,此时速度为
,打开伞后伞兵以
的加速度竖直向下做匀减速运动,伞兵落地时速度恰好为
。求:
(1)伞兵打开伞时的速度大小
(2)伞兵打开伞时的离地高度
19.在疫情期间,智能送餐机器人可以尽量减少人员的接触,图为某款智能送餐机器人。某次机器人给
远处的顾客送菜,机器人从静止开始加速,
后速度达到
,然后做匀速直线运动,距离顾客
时开始减速,到达顾客身边恰能停止,机器人加速、减速阶段均可视为匀变速直线运动。求机器人:
(1)匀加速阶段的加速度大小;
(2)匀减速阶段的时间;
(3)整个送餐过程的平均速度大小。
20.甲、乙两车相距16.5m且甲在前乙在后,它们同时向同一方向运动,其中甲以15m/s的速度匀速行驶,乙以3m/s2的加速度由静止开始做匀加速直线运动,求
(1)甲、乙两车何时相距最远,最远距离多大?
(2)乙车何时能赶上甲车,此时乙车的速度是多大?
答案解析部分
一、单选题
1.【答案】
A
【解析】【解答】A.对比初速度为零的匀加速直线位移公式
可知,丙质点做匀加速直线运动,A符合题意;
BD.甲朝正方向做匀速直线运动,乙朝负方向做匀速直线运动,故甲、乙两个质点运动方向不同,BD不符合题意;
C.
时甲、乙两质点距离最远,C不符合题意。
故答案为:A。
【分析】根据运动图像画出两个物体的运动简图,由运动学公式列方程求解。
2.【答案】
B
【解析】【解答】设窗户上沿到物体下落点的距离为h,下落时间为t1
,
则有
到窗户下沿则有
联立可得
楼层数约为
因为该同学家在二楼,所以估计丢物住户的楼层是17楼.
故答案为:B。
【分析】利用自由落体的位移公式可以求出楼层的高度,结合每层楼的高度可以求出楼层的层数。
3.【答案】
D
【解析】【解答】AB.根据斜率等于速度可知,质点的速度先沿正方向,后沿负方向,质点一定做直线运动。AB不符合题意;
C.在t1时刻质点的位移为零,表示质点在t1时刻回到出发点,C不符合题意;
D.由斜率看出,质点的速度先减小后增大,D符合题意。
故答案为:D。
【分析】位移的图象只规定了两个方向所以质点做直线运动;利用图象斜率可以判别速度的变化;利用坐标可以判别其位移的大小。
4.【答案】
B
【解析】【解答】A.根据v-t图象的意义可知,某点处切线的斜率表示该点处的加速度,由题图可知,0~66?s内快艇做加速度逐渐减小的加速直线运动,A不符合题意;
BC.66s时快艇开始减速,96s时减速到零,此时离商船最近,然后开始调头,B符合题意,C不符合题意;
D.96~116s内,加速度为负且为定值,说明快艇反方向做匀加速直线运动,D不符合题意。
故答案为:B。
【分析】v-t图像的斜率大小表示速度大小,正负表示速度方向,图像与坐标轴围城的面积表示这段时间内的位移,即可求解。
5.【答案】
B
【解析】【解答】A.t=1.8s时,甲、乙两质点速度均为
A正确,不合题意;
B.t=1.8s时,甲、乙两质点位置相同,二者相遇,B错误,符合题意;
C.0~2.5s,甲的平均速度和平均速率均为
C正确,不合题意;
D.根据
可得在2.5s时刻,乙的纵坐标x=1.7×3m=5.1m,D正确,不合题意。
故答案为:B。
【分析】利用初末位置坐标及运动的时间可以求出两质点的速度大小;利用交点可以判别两个物体相遇;利用位移和时间可以求出平均速度的大小;利用乙的速度可以求出其末坐标的大小。
6.【答案】
C
【解析】【解答】根据v2=2gh可得
因运动员竖直跳起将篮球扣入栏中,可知起跳的略大于3.2m/s;
故答案为:C。
【分析】运动员做竖直上抛运动,利用速度位移公式可以求出起跳速度的大小。
7.【答案】
C
【解析】【解答】A.刹车时汽车做匀减速运动的总时间为
A不符合题意;
B.刹车时汽车在5s末汽车已经停止,则6s末的速度大小为0,B不符合题意;
C.刹车时汽车在前
内通过的位移为
C符合题意;
D.刹车时汽车通过的总位移为
D不符合题意。
故答案为:C。
【分析】运用匀变速运动的速度公式可以求得时间,汽车刹车计算速度时要注意刹车停止的时间,运用匀变速的位移公式求位移即可。
8.【答案】
D
【解析】【解答】A.乙物体
末开始做加速运动,加速度大小为
A不符合题意;
B.根据图像和时间轴围成的面积表示位移,则
时,甲乙位移不同,甲、乙两物体从同一地点出发,则乙物体没有追上甲物体,B不符合题意;
C.根据图像和时间轴围成的面积表示位移,乙物体在前
内通过的位移
C不符合题意;
D.在10~20s内,甲的速度大于乙的速度,甲比乙运动得快,甲在乙的前方,两者距离逐渐增大;20s后,乙的速度大于甲的速度,乙比甲运动得快,两者距离逐渐减小,在t=20s时刻两者距离最大,D符合题意。
故答案为:D。
【分析】速度图象反映物体速度随时间的变化情况,可直接读出速度的大小;速度图象的“面积”大
小等于物体通过的位移大小,根据位移关系即可分析乙何时追上甲;根据速度的大小关系,判断两者距离的变化.
9.【答案】
A
【解析】【解答】根据
可得第3节车厢经过他的时间为
解得
故答案为:A。
【分析】利用匀变速直线运动的位移公式结合其三节车厢运动时间和两节车厢运动时间的差值可以求出加速度的大小。
10.【答案】
D
【解析】【解答】A.由图可知,甲车在0-4s内的加速度大小为1m/s2
,
A不符合题意;
B.甲车0-4s内与4-6s内的速度方向相同,B不符合题意;
C.由图4-6s内甲车的加速度为-4m/s2
,
甲车从4s末经过
与乙车速度相等。
所以从运动开始经过5s甲乙两车速度相等,在5s之前甲车速度大于乙车,甲乙之间的距离越来越大,5s之后甲车速度小于乙车,甲乙之间的距离越来越小,所以在乙追上甲之前,5s末两小车相距最远,C不符合题意;
D.根据图像,可知甲车在0-8s内的位移
乙车在0-8s内的位移
所以8s末甲、乙两小车相遇,且离出发点距离为32m,D符合题意。
故答案为:D。
【分析】利用图像斜率可以求出加速度的大小;利用速度的符号可以判别速度的方向;两车其速度相等时其距离最大;利用面积的大小可以求出汽车的位移。
二、多选题
11.【答案】
B,C
【解析】【解答】A.质点做直线运动的
图像是抛物线的一部分,说明质点做的是匀变速直线运动,A不符合题意;
B.根据抛物线的特点,图线在
、
时刻的斜率大小相等,故质点在
、
时刻的速度大小相等,B符合题意;
C.质点从
时刻至
时刻通过的位移为零,可知质点在这段时间内的平均速度为零,C符合题意;
D.从
时刻至
时刻,质点先由
向
位置运动,再由
向
位置运动,通过的路程为
,D不符合题意。
故答案为:BC。
【分析】利用图线为抛物线所以可以判别质点做匀变速直线运动其加速度保持不变;利用图像斜率可以判别速度的大小;利用初末位置可以求出位移的大小,除以对应时间可以求出平均速度的大小;利用质点的位置可以求出通过的路程的大小。
12.【答案】
B,D
【解析】【解答】ABC.小球A自由下落,小球B从等高处水平抛出,要想击中A球,必须两个小球下落的高度相等,小球B在竖直方向做自由落体运动,所以必须同时抛出才能击中,AC不符合题意B符合题意;
D.小球B斜向上抛出,小球B在竖直方向上做竖直上抛运动,A小球做自由落体运动,不能击中,D符合题意。
故答案为:BD。
【分析】根据自由落体运动与抛体运动的规律结合运动学公式列方程求解。
13.【答案】
A,C,D
【解析】【解答】A.根据v-t图像的斜率表示加速度,知甲的加速度大小为
乙车的加速度大小为
故乙车的加速度大小是甲车的2倍,
A符合题意;
B.由v-t图像与时间轴所围成的面积表示物体发生的位移,可判断0~10s时两车通过的位移不相同,且乙车发生的位移大于甲车发生的位移,B不符合题意;
C.乙车在t=15s时停止运动,此时甲的速度为
,乙车停止运动后,甲车又运动了
C符合题意;
D.若行进中两车恰好没有发生碰撞,说明t=10s时刻两车速度相等时恰好相遇,则t=0时刻两车间距等于两车等于在0-10s内位移之差,如图中虚线面积
D符合题意。
故答案为:ACD。
【分析】利用图像斜率可以求出加速度的大小;利用图像面积可以求出位移的大小;利用图像面积可以求出运动的位移;利用共速时两车相遇结合面积可以求出最初两车相距的距离。
14.【答案】
A,C
【解析】【解答】AB.竖直上抛的小球,不计阻力时只受到自身重力作用,为匀减速,加速度
,上升到最高点时,速度为0。根据匀变速直线运动有
得到
A符合题意,B不符合题意;
CD.上升过程运动时间
C符合题意,D不符合题意。
故答案为:AC。
【分析】利用竖直上抛运动的速度位移公式可以求出上升的最大高度,结合速度公式可以求出运动的时间。
15.【答案】
A,C
【解析】【解答】AB.竖直上抛的小球,不计阻力时只受到自身重力作用,为匀减速,加速度
,小球上升到最高点时,速度为0,最高点时依然受重力作用,加速度
,A符合题意,B不符合题意;
C.上升过程根据匀变速直线运动规律有
解得
C符合题意;
D.上升过程运动时间
则小球从抛出到落地所用的时间为6s,D不符合题意。
故答案为:AC。
【分析】小球到达最高点时速度等于0其加速度等于重力加速度;利用速度位移公式可以求出最大的高度;利用速度公式可以求出运动的时间。
16.【答案】
B,D
【解析】【解答】A.根据x-t图象的斜率表示速度,知0~2s内甲物体沿正向做速度为2m/s的匀速直线运动,乙沿正向做初速度为0的匀加速直线运动,甲的速度先大于乙的速度,后小于乙的速度,则知甲、乙两物体之间的距离先增大后减小,A不符合题意;
B.根据x-t图象的斜率表示速度,知第3秒内甲的速度为负。由v-t图象知第3秒内乙物体速度为正,则第3秒内甲、乙两物体速度方向相反,B符合题意;
C.2~4s内,甲做负方向的匀速直线运动,乙2~3s做正方向匀减速直线运动,3~4s做负方向匀加速直线运动,C不符合题意;
D.6s末,甲的位移为零,v-t与时间轴所围的“面积”表示位移,知t=6s时,乙的位移为零,故6s末,甲、乙两物体均回到原出发点,D符合题意。
故答案为:BD。
【分析】利用位移时间图像的斜率可以判别甲车的速度,利用两车的速度比较可以判别两车距离的变化;利用位移图像斜率可以判别速度的方向,利用速度方向可以判别速度的方向;利用图像斜率可以判别甲的速度变化;利用位移时间图像的坐标可以判别甲的位移;利用速度时间图像的面积可以判别乙的位移。
17.【答案】
B,C
【解析】【解答】A.设加速的末速度为v,则有
加速、减速中的加速度大小之比
A不符合题意;
BD.根据匀变速直线运动的平均速度公式
得,加速、减速中的平均速度大小之比
B符合题意,D不符合题意;
C.根据位移公式
得,加速、减速中的位移之比
C符合题意。
故答案为:BC。
【分析】利用速度公式可以求出加速和减速的加速度比值;利用初末速度之和的一半可以求出平均速度的比值;利用平均速度结合运动时间可以求出位移的比值。
三、综合题
18.【答案】
(1)由自由落体速度公式可得
解得伞兵打开伞时的速度大小为
(2)打开伞后下落过程,由位移公式可得
解得伞兵打开伞时的离地高度为
【解析】【分析】(1)根据自由落体运动的速度公式列方程求解。
(2)由下落过程中速度与位移的关系列方程求解。
19.【答案】
(1)解:在加速过程由
可得
(2)解:在减速过程由
可得
(3)解:在加速度过程由
可得
则匀速过程
得
则全程的平均速度大小由
可得
【解析】【分析】(1)机器人做匀加速直线运动,利用加速度的定义式可以求出加速度的大小;
(2)机器人做匀减速直线运动,利用平均速度公式可以求出运动的时间;
(3)在加速过程中,利用平均速度公式可以求出机器人的位移,利用匀速运动的位移公式可以求出机器人匀速运动过程的时间,利用全程的位移和全程的运动时间可以求出平均速度的大小。
?
?
20.【答案】
(1)解:当两车的速度相等时,相距最远v1=at1
可得
甲车运动的距离
乙车运动的距离
此时相距的最远距离
(2)解:设经过t时间乙车追上甲车,有
代入数据解得t=11s
此时乙车的速度v2=at=3×11m/s=33m/s
【解析】【分析】(1)当两车速度相等时两车距离最远,乙车做匀加速直线运动,甲车做匀速直线运动,利用速度公式可以求出乙车加速的时间,结合两车的位移公式可以求出两车之间的距离;
(2)经过一段时间后乙车追上甲车,利用位移相等结合两车的位移公式可以求出相遇的时间,利用乙车的速度公式可以求出乙车速度的大小。
1
/
3
