第11章 图形的全等 单元测试卷(B)(含答案)
文档属性
| 名称 | 第11章 图形的全等 单元测试卷(B)(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 120.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-30 00:00:00 | ||
图片预览

文档简介
第11章 图形的全等 单元测试卷(B)
(满分:100分 时间:60分钟)
一、选择题(每题3分,共30分)
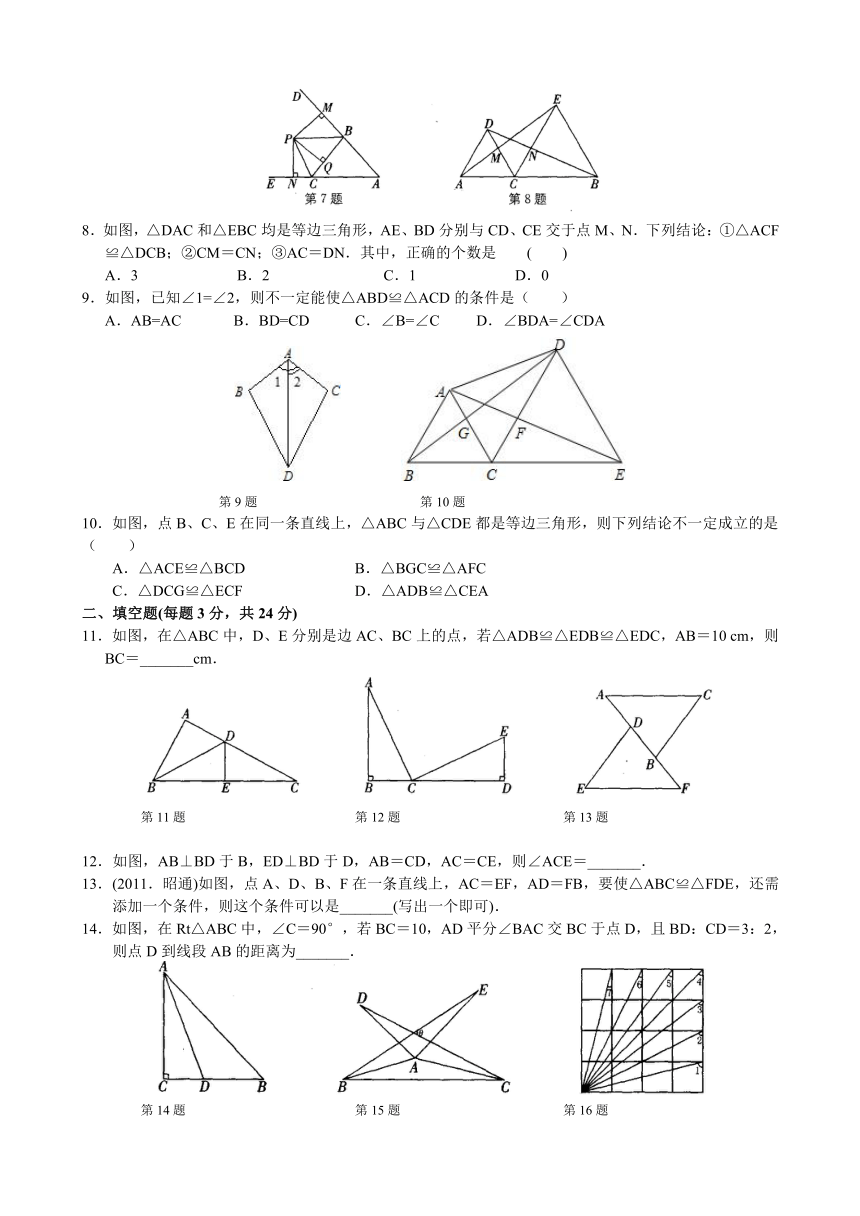
1.小明用如图所示的胶滚沿从左到右的方向将图案滚涂到墙上,下列给出的四个图案中,符合图示胶滚涂出的图案的是 ( )
2.下列结论错误的是 ( )
A.全等三角形对应边上的高相等
B.全等三角形对应边上的中线相等
C.两个直角三角形中,斜边和一个锐角对应相等,则这两个三角形全等
D.两个直角三角形中,两个锐角相等,则这两个三角形全等
3.(2011.江西)如图,下列条件中,不能说明△ABD≌△ACD的是 ( )
A.BD=DC,AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D.∠B=∠C,BD=DC
4.如图,下列四组条件:①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;③∠B=∠E,BC=FF,∠C=∠F;④AB=DE,AC=DF,∠B=∠E.其中,能使△ABC≌△DEF的条件共有 ( )
A.1组 B.2组 C.3组 D.4组
5.如图,AB=AC,要说明△ADC≌△AEB,则需添加的条件不能是 ( )
A.∠B=∠C B.AD=AE C.∠ADC=∠AEB D.DC=BE
6.如图,∠E=∠F=90°,∠B=∠C,AE=AF,下列结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△CAN≌△BAM.其中,正确的有 ( )
A.1个 B.2个 C.3个 D.4个
7.如图,∠DBC和∠ECB是△ABC的两个外角,P是∠DBC、∠ECB两平分线的交点,PM、PN、PQ分别是P点到AB、AC、BC三边的垂线段.PM、PN、PQ的数量关系是 ( )
A.PM>PN>PQ B.PMC.PM=PN=PQ D.PM=PN>PQ
8.如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N.下列结论:①△ACF≌△DCB;②CM=CN;③AC=DN.其中,正确的个数是 ( )
A.3 B.2 C.1 D.0
9.如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
A.AB=AC B.BD=CD C.∠B=∠C D.∠BDA=∠CDA
第9题 第10题
10.如图,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是( )
A.△ACE≌△BCD B.△BGC≌△AFC
C.△DCG≌△ECF D.△ADB≌△CEA
二、填空题(每题3分,共24分)
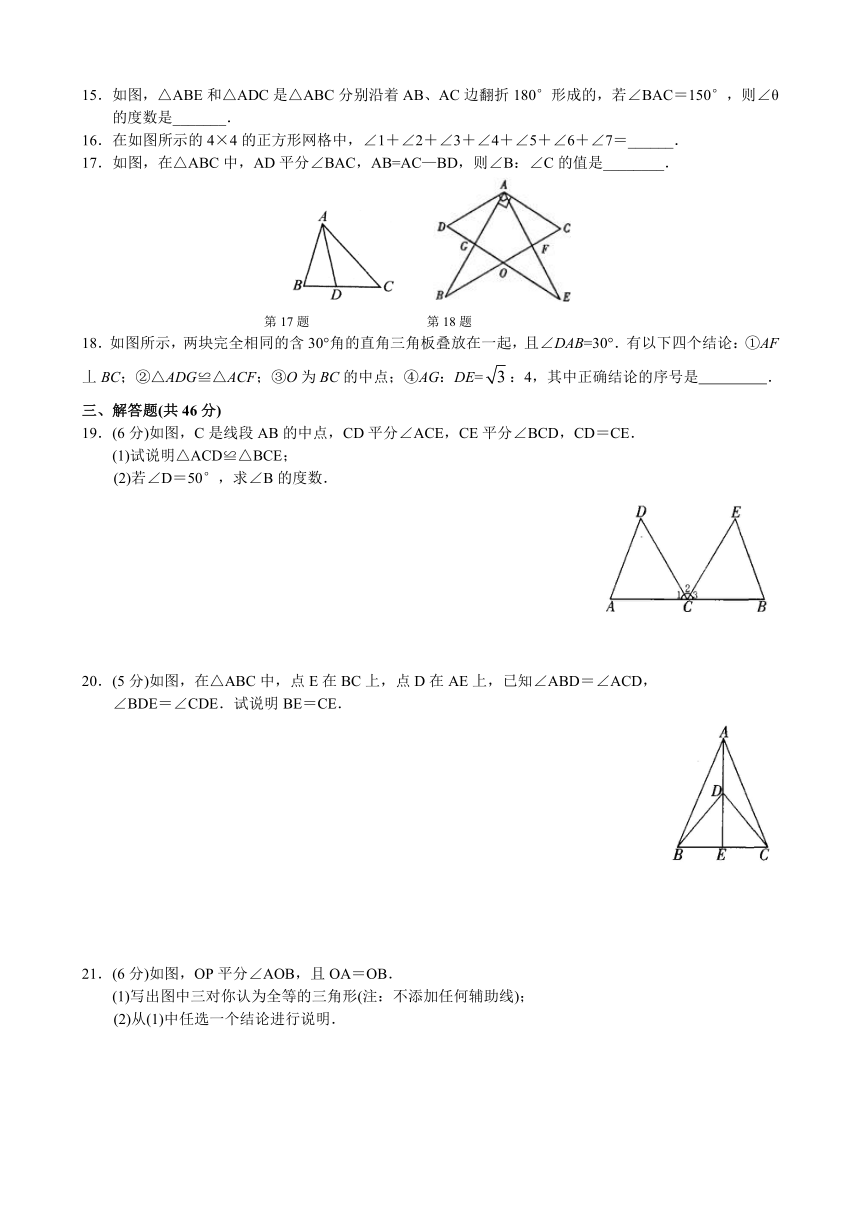
11.如图,在△ABC中,D、E分别是边AC、BC上的点,若△ADB≌△EDB≌△EDC,AB=10 cm,则BC=_______cm.
第11题 第12题 第13题
12.如图,AB⊥BD于B,ED⊥BD于D,AB=CD,AC=CE,则∠ACE=_______.
13.(2011.昭通)如图,点A、D、B、F在一条直线上,AC=EF,AD=FB,要使△ABC≌△FDE,还需添加一个条件,则这个条件可以是_______(写出一个即可).
14.如图,在Rt△ABC中,∠C=90°,若BC=10,AD平分∠BAC交BC于点D,且BD:CD=3:2,则点D到线段AB的距离为_______.
第14题 第15题 第16题
15.如图,△ABE和△ADC是△ABC分别沿着AB、AC边翻折180°形成的,若∠BAC=150°,则∠θ的度数是_______.
16.在如图所示的4×4的正方形网格中,∠1+∠2+∠3+∠4+∠5+∠6+∠7=______.
17.如图,在△ABC中,AD平分∠BAC,AB=AC—BD,则∠B:∠C的值是________.
第17题 第18题
18.如图所示,两块完全相同的含30°角的直角三角板叠放在一起,且∠DAB=30°.有以下四个结论:①AF丄BC;②△ADG≌△ACF;③O为BC的中点;④AG:DE=:4,其中正确结论的序号是 .
三、解答题(共46分)
19.(6分)如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.
(1)试说明△ACD≌△BCE;
(2)若∠D=50°,求∠B的度数.
20.(5分)如图,在△ABC中,点E在BC上,点D在AE上,已知∠ABD=∠ACD,
∠BDE=∠CDE.试说明BE=CE.
21.(6分)如图,OP平分∠AOB,且OA=OB.
(1)写出图中三对你认为全等的三角形(注:不添加任何辅助线);
(2)从(1)中任选一个结论进行说明.
22.(6分)如图,在△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F;过B作BD⊥BC,交CF的延长线于D.
(1)试说明AE=CD;
(2)若AC=12 cm,求BD的长.
23.(6分)(2011.内江)在Rt△ABC中,∠BAC=90°,AC=2AB.D是AC的中点,将一把锐角为45°的直角三角尺如图放置,使三角尺斜边的两个端点分别与点A、D重合,连接BE、EC.试猜想线段BE和EC的数量及位置关系,并说明理由.
24.(8分)如图,D是△ABC的边BC上的点,且CD=AB,∠ADB=∠BAD.AE是△ABD的中线,试说明AC=2AE.
25.(8分) (2011.牡丹江)在△ABC中,∠ACB=2∠B,如图①,当∠C=90°,AD为∠ABC的角平分线时,在AB上截取AE=AC,连接DE,易证AB=AC+CD.
(1)如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的数量关系?不需要证明,请直接写出你的猜想:
(2)如图③,当AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.
参考答案
一、1.A 2.D 3.D 4.C 5.D 6.C 7.C 8.B 9.B 10.D
二、11.20 12.90 13.答案不惟一 14.4 15.60° 16.315°
17.2 18.①②③④
三、19.(1)略 (2)70° 20.略 21.(1)答案不惟一 (2)答案不惟一
22.(1)略 (2)6cm 23.BE=EC,BE⊥EC 24.略
(1)猜想:AB=AC+CD.
证明:如图②,在AB上截取AE=AC,连接DE,
∵AD为△ABC的角平分线时,∴∠BAD=∠CAD,
∵AD=AD,∴△ADE≌△ADC(SAS),∴∠AED=∠C,ED=CD,
∵∠ACB=2∠B,∴∠AED=2∠B,∴∠B=∠EDB,∴EB=ED,∴EB=CD,
∴AB=AE+DE=AC+CD.
(2)猜想:AB+AC=CD.
证明:在BA的延长线上截取AE=AC,连接ED.
∵AD平分∠FAC,∴∠EAD=∠CAD.
在△EAD与△CAD中,AE=AC,∠EAD=∠CAD,AD=AD,
∴△EAD≌△CAD.∴ED=CD,∠AED=∠ACD.∴∠FED=∠ACB.
又∠ACB=2∠B,∠FED=∠B+∠EDB,∠EDB=∠B.
∴EB=ED.
∴EA+AB=EB=ED=CD.
∴AC+AB=CD.
(满分:100分 时间:60分钟)
一、选择题(每题3分,共30分)
1.小明用如图所示的胶滚沿从左到右的方向将图案滚涂到墙上,下列给出的四个图案中,符合图示胶滚涂出的图案的是 ( )
2.下列结论错误的是 ( )
A.全等三角形对应边上的高相等
B.全等三角形对应边上的中线相等
C.两个直角三角形中,斜边和一个锐角对应相等,则这两个三角形全等
D.两个直角三角形中,两个锐角相等,则这两个三角形全等
3.(2011.江西)如图,下列条件中,不能说明△ABD≌△ACD的是 ( )
A.BD=DC,AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D.∠B=∠C,BD=DC
4.如图,下列四组条件:①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E,BC=EF;③∠B=∠E,BC=FF,∠C=∠F;④AB=DE,AC=DF,∠B=∠E.其中,能使△ABC≌△DEF的条件共有 ( )
A.1组 B.2组 C.3组 D.4组
5.如图,AB=AC,要说明△ADC≌△AEB,则需添加的条件不能是 ( )
A.∠B=∠C B.AD=AE C.∠ADC=∠AEB D.DC=BE
6.如图,∠E=∠F=90°,∠B=∠C,AE=AF,下列结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△CAN≌△BAM.其中,正确的有 ( )
A.1个 B.2个 C.3个 D.4个
7.如图,∠DBC和∠ECB是△ABC的两个外角,P是∠DBC、∠ECB两平分线的交点,PM、PN、PQ分别是P点到AB、AC、BC三边的垂线段.PM、PN、PQ的数量关系是 ( )
A.PM>PN>PQ B.PM
8.如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N.下列结论:①△ACF≌△DCB;②CM=CN;③AC=DN.其中,正确的个数是 ( )
A.3 B.2 C.1 D.0
9.如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
A.AB=AC B.BD=CD C.∠B=∠C D.∠BDA=∠CDA
第9题 第10题
10.如图,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是( )
A.△ACE≌△BCD B.△BGC≌△AFC
C.△DCG≌△ECF D.△ADB≌△CEA
二、填空题(每题3分,共24分)
11.如图,在△ABC中,D、E分别是边AC、BC上的点,若△ADB≌△EDB≌△EDC,AB=10 cm,则BC=_______cm.
第11题 第12题 第13题
12.如图,AB⊥BD于B,ED⊥BD于D,AB=CD,AC=CE,则∠ACE=_______.
13.(2011.昭通)如图,点A、D、B、F在一条直线上,AC=EF,AD=FB,要使△ABC≌△FDE,还需添加一个条件,则这个条件可以是_______(写出一个即可).
14.如图,在Rt△ABC中,∠C=90°,若BC=10,AD平分∠BAC交BC于点D,且BD:CD=3:2,则点D到线段AB的距离为_______.
第14题 第15题 第16题
15.如图,△ABE和△ADC是△ABC分别沿着AB、AC边翻折180°形成的,若∠BAC=150°,则∠θ的度数是_______.
16.在如图所示的4×4的正方形网格中,∠1+∠2+∠3+∠4+∠5+∠6+∠7=______.
17.如图,在△ABC中,AD平分∠BAC,AB=AC—BD,则∠B:∠C的值是________.
第17题 第18题
18.如图所示,两块完全相同的含30°角的直角三角板叠放在一起,且∠DAB=30°.有以下四个结论:①AF丄BC;②△ADG≌△ACF;③O为BC的中点;④AG:DE=:4,其中正确结论的序号是 .
三、解答题(共46分)
19.(6分)如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.
(1)试说明△ACD≌△BCE;
(2)若∠D=50°,求∠B的度数.
20.(5分)如图,在△ABC中,点E在BC上,点D在AE上,已知∠ABD=∠ACD,
∠BDE=∠CDE.试说明BE=CE.
21.(6分)如图,OP平分∠AOB,且OA=OB.
(1)写出图中三对你认为全等的三角形(注:不添加任何辅助线);
(2)从(1)中任选一个结论进行说明.
22.(6分)如图,在△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作CF⊥AE,垂足为F;过B作BD⊥BC,交CF的延长线于D.
(1)试说明AE=CD;
(2)若AC=12 cm,求BD的长.
23.(6分)(2011.内江)在Rt△ABC中,∠BAC=90°,AC=2AB.D是AC的中点,将一把锐角为45°的直角三角尺如图放置,使三角尺斜边的两个端点分别与点A、D重合,连接BE、EC.试猜想线段BE和EC的数量及位置关系,并说明理由.
24.(8分)如图,D是△ABC的边BC上的点,且CD=AB,∠ADB=∠BAD.AE是△ABD的中线,试说明AC=2AE.
25.(8分) (2011.牡丹江)在△ABC中,∠ACB=2∠B,如图①,当∠C=90°,AD为∠ABC的角平分线时,在AB上截取AE=AC,连接DE,易证AB=AC+CD.
(1)如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的数量关系?不需要证明,请直接写出你的猜想:
(2)如图③,当AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.
参考答案
一、1.A 2.D 3.D 4.C 5.D 6.C 7.C 8.B 9.B 10.D
二、11.20 12.90 13.答案不惟一 14.4 15.60° 16.315°
17.2 18.①②③④
三、19.(1)略 (2)70° 20.略 21.(1)答案不惟一 (2)答案不惟一
22.(1)略 (2)6cm 23.BE=EC,BE⊥EC 24.略
(1)猜想:AB=AC+CD.
证明:如图②,在AB上截取AE=AC,连接DE,
∵AD为△ABC的角平分线时,∴∠BAD=∠CAD,
∵AD=AD,∴△ADE≌△ADC(SAS),∴∠AED=∠C,ED=CD,
∵∠ACB=2∠B,∴∠AED=2∠B,∴∠B=∠EDB,∴EB=ED,∴EB=CD,
∴AB=AE+DE=AC+CD.
(2)猜想:AB+AC=CD.
证明:在BA的延长线上截取AE=AC,连接ED.
∵AD平分∠FAC,∴∠EAD=∠CAD.
在△EAD与△CAD中,AE=AC,∠EAD=∠CAD,AD=AD,
∴△EAD≌△CAD.∴ED=CD,∠AED=∠ACD.∴∠FED=∠ACB.
又∠ACB=2∠B,∠FED=∠B+∠EDB,∠EDB=∠B.
∴EB=ED.
∴EA+AB=EB=ED=CD.
∴AC+AB=CD.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
