(小升初真题专项)六年级数学找规律题(易错题、难题)名师详解连载六
文档属性
| 名称 | (小升初真题专项)六年级数学找规律题(易错题、难题)名师详解连载六 |  | |
| 格式 | doc | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-09 22:18:57 | ||
图片预览




文档简介
(小升初真题)六年级数学找规律题(易错题、难题)名师详解连载六
1.0.234823482348…,这个纯循环小数的小数点后面第99位上的数字是( )
A.2 B.3 C.4 D.8
2.观察下列式子:0.2=123÷999,0.3=237÷999,0.4=45÷999,那么,0.5等于( )
A.0.45÷999 B.4.5÷999 C.45÷999 D.450÷999
3.一列分数的前4个是、、、.根据这4个分数的规律可知,第8个分数是( )
A. B. C. D.
4.21.78÷0.4=54.45
219.78÷0.4=549.45
2199.78÷0.4=5499.45……
按照上面的规律,下面正确的等式是( )
A.219999.78÷0.4=54999.45 B.2199.78÷0.4=54999.45
C.21999.78÷0.4=5499.945 D.219999.78÷0.4=549999.45
填在如图各正方形中的四个数之间都有相同的规律,根据此规律,m的值是( )
A.38 B.52 C.66 D.74
1.依据图中的规律,在括号里填上适当的分数。
2.先观察前面三道题,再填出横线里的数.
1×9+2=11,12×9+3=111,123×9+4=1111,1234×9+ = ,
×9+ =1111111.
3.奇妙的算式.
5×5=25
95×95=9025
995×995=990025
9995×9995=99900025
99995×99995= .
4.根据已有的结果找出规律,直接写得数.
6.6×6.7=44.22 66.666×66.667=
66.6×66.7=4442.22 666.666×666.667=
666.6×666.7=444422.22 6.666666×6666.667=
5.23.12.34,12.43,13.24,13.42,…,43.12,43.21,在这组数中,自左往右数,第19个数是多少?
1.将2化成循环小数是 ,小数点右边第2014位上的数字是 .
2.有一列数,第一个数是100,第二个数是90,从第三个数开始,每个数都是它前面两个数的平均数.第三十个数的整数部分是 .
3.一个同学暑假参加爬梯子闯关游戏,当他爬到梯子正中间时,二楼窗口喷出水来,他就往下退了3级,等到水过去了,他又爬了7级,这时屋顶有小沙包掉下来,他又往后退了2级,幸好没滑下,他又爬了8级,这时他距梯子最高层还有1级,问这个梯子共有 级.
4.按规律填数.
(1)2,5,8,11, , .
(2),,,, , .
(3),,,, , .
(4)
5.按规律填数.
(1)0.2、1.1、2.2、3.5、 、 .
(2)
1.桌上有1张纸,第一次把它剪成3块放回桌上;第二次从桌上拿起1块剪成3块后放回桌上;….进行了这样的8次操作后,桌上一共有( )块纸.
A.24 B.21 C.19 D.17
2.根据各式的规律填空:
1=12
1+3=22
1+3+5=32
1+3+5+7=42
(1)1+3+5+7+9+11+13= 2.(2)从1开始, 个连续奇数相加的和是202.
3.在生产和生活中,我们经常把一些同样大小的圆柱管捆扎起来,下面我们来探索捆扎一圈时绳子的长度.假设每个圆柱管的外直径都是10厘米,圆柱管的放置时“单层平放”,打结处绳子的长度不计,捆扎后横截面如下所示:
(1)探索:
个数 图形 绳子长度
1
厘米
2
厘米
3
厘米
… … …
(2)推想:
①当圆柱管的个数是10时,所用绳子的长度是 厘米.
②当圆柱管的个数是a时,所用绳子的长度是 厘米.
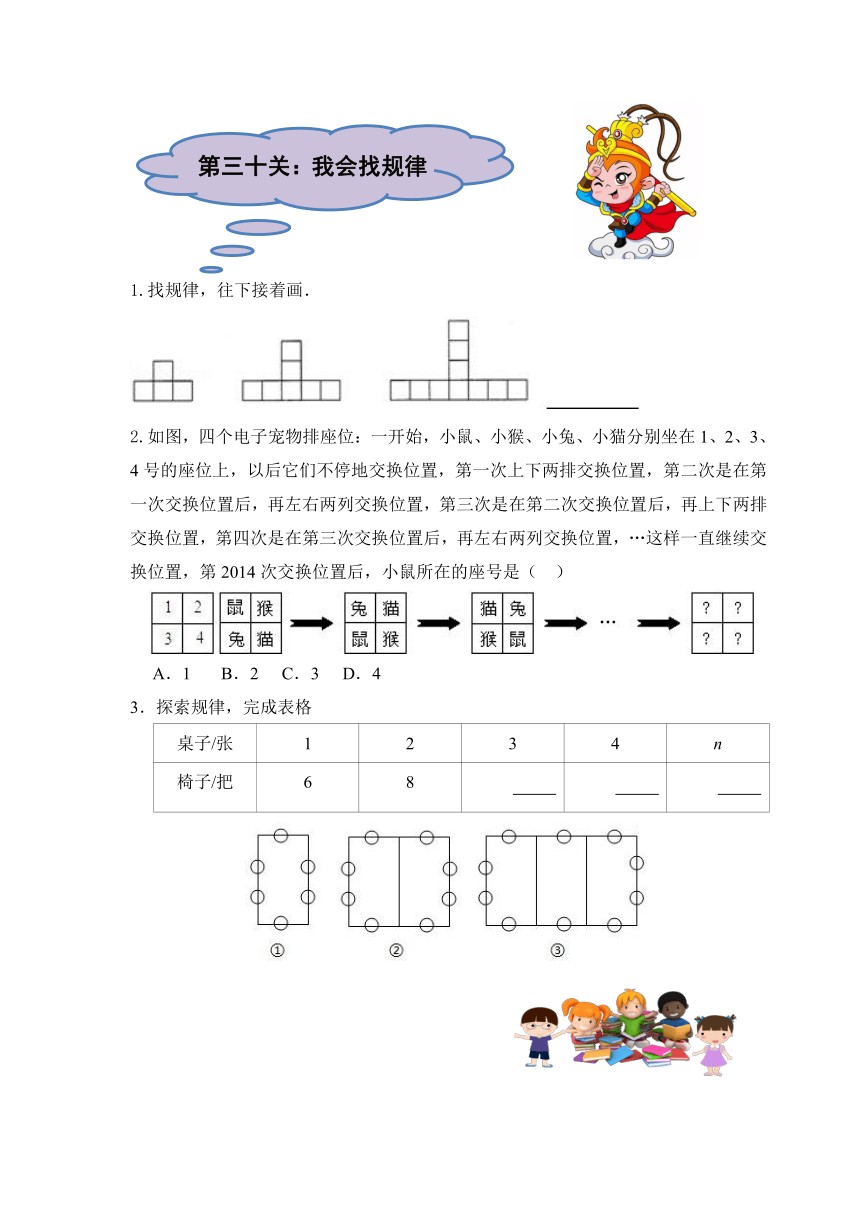
1.找规律,往下接着画.
2.如图,四个电子宠物排座位:一开始,小鼠、小猴、小兔、小猫分别坐在1、2、3、
4号的座位上,以后它们不停地交换位置,第一次上下两排交换位置,第二次是在第一次交换位置后,再左右两列交换位置,第三次是在第二次交换位置后,再上下两排交换位置,第四次是在第三次交换位置后,再左右两列交换位置,…这样一直继续交换位置,第2014次交换位置后,小鼠所在的座号是( )
A.1 B.2 C.3 D.4
3.探索规律,完成表格
桌子/张 1 2 3 4 n
椅子/把 6 8
参考答案及难题详解
第二十六关
1.解:0.234823482348…的循环节是2348,是4位数,
99÷4=24…3,从循环节的首位起第三位上的数字是4;
答案:C.
2.解:观察已知三个算式,当除数是999时,将被除数小数点向左移动3位,然后在十分位和千分位的数字上加上循环符号,就是算式的商,
所以,已知商为0.5,将循环符号去掉,然后小数点向右移动三位就是被除数,即
450,得到算式:0.5=450÷999 答案:D。
3.解:第8个数的分子是8;
由前4个分数是、、、可知,分子是1、2、3、4.
第n个分数的分子就是n,所以第8个数的分子是8;
分母是2,5,10、17,观察可知:?
2=1?+1,?5=2?+1, 10=3?+1,?17=4?+1,
则第n个分数的分母为n?+1,所以第8个分数的分母为8?+1=65,
即第8个分数是; 答案:C.
4.解:21.78÷0.4=54.45
219.78÷0.4=549.45
2199.78÷0.4=5499.45
……
219999.78÷0.4=549999.45
……
答案:D.
5..解:根据图形的规律,第4个图形:
左下应该是6+2=8
右上数字为:6+4=10
右下数字为:8×10﹣6=74
答:m的值是74.答案:D.
第二十七关
1.解:分子构成的数列为:3,5,7,9,11,13,……;
分母构成的规律用式子表示为:1+3=4,4+5=9,9+7=16,16+9=25,25+11=36,36+13=49,……。
故第6层的分数为
2.解:1×9+2=11,12×9+3=111,123×9+4=1111,1234×9+5=11111,123456×9+7=1111111;
答案:5,11111,123456,7。
3.解:认真观察5×5=25
95×95=9025
995×995=990025
9995×9995=99900025 得出规律,因数在5的前面有几个9,则在积中25的前面就有几个9和几个0,
所以,99995×99995=9999000025;
答案:9999000025.
4.解:根据已有的结果找出规律,直接写得数.
6.6×6.7=44.22 66.666×66.667=4444.422222
66.6×66.7=4442.22 666.666×666.667=444444.222222
666.6×666.7=444422.22 6.66666×6666.667=44444.442222222
5.解:12.34,12.43,13.24,13.42,…,43.12,43.21,是用1、2、3、4这四个数字和小数点组成的两位小数,然后把这些两位小数按照从小到大排列
一共有:4×3×2×1=24(个)
第24个是:43.21,第23个是:43.12,第22个是:34.21,第21个是:34.12,第20个是:24.31,第19个是:24.13.
答:第19个数是24.13.
第二十八关
1.解:2=2.1428
小数部分是7、1、4、2、8、5六个数字的循环小数,
2014÷6=335…4
余数是4,所以小数点右边第2014位上的数字是一个循环的第4个数字2;
答案:2.1428,2.
2.解:(100+90)÷2=95,(95+90)÷2=92.5,(95+92.5)÷2=93.75,(93.75+92.5)÷2=93,(93.5+93)÷2=93.25,(93.25+93)÷2=93.125,
前面两个数一定都是90多,其平均数一定也是90多,所以无论第几个整数部分都是93(除了第一组,第二 组);即从第五个数起每个数的整数部分是93.
答案:93.
3.解:设中间一级为第x级,则全梯共有2x﹣1级,根据题意得:
x﹣3+7﹣2+8+1=2x﹣1
x=12
2x﹣1=2×12﹣1=23.
答:这个梯子共有23级.
答案:23.
解:
(1)11+3=14, 14+3=17;
(2)=; =;
(3)分母:6×6=36, 分子:36﹣1=35,
这个分数是:;
分母:7×7=49, 分子:49﹣1=48,
这个分数是:.
(4)(58﹣10)÷6,
=48÷6,
=8;
所以是这个数列的第9项,它的分子就是10.即这个分数是.
5.(1)5、6.7.根据已知的数可得排列规律:从0.2开始每次递增0.9、1.1、1.3、1.5、1.7、1.9;据此解答。
(2)答案:20,22,24;50,45,40。
第二十九关
1.解:由以上分析可知,第八次操作后的块数是:
3+2×(8﹣1)=17(块) 答案:D.
2.(1)1+3+5+7+9+11+13=72;
(2)观察图形可知,从1开始的连续奇数的和等于奇数个数的平方,
所以从1开始,20个连续奇数相加的和是202.
答案:(1)7;(2)20.
3.解:①π×10=10π(厘米);②10π+20(厘米);
③10π+20×2=10π+40(厘米);
统计表如下:
个数 图形 绳子长度
1
10π厘米
2
10π+20厘米
3
10π+40厘米
… … …
(2)①当圆柱管的个数是10时,所用绳子的长度是:
10π+20×(10﹣1)=10π+180(厘米);
②当圆柱管的个数是a时,所用绳子的长度是:
10π+(a﹣1)×10×2
=10π+a×10﹣1×10×2
=10π+20a﹣20(厘米);
答案:10π+180;10π+20a﹣20.
第二十九关
1.
2.解:根据题意,可得
第一次交换位置后,小鼠所在的座号是3号;
第二次交换位置后,小鼠所在的座号是4号;
第三次交换位置后,小鼠所在的座号是2号;
第四次交换位置后,小鼠所在的座号是1号;
第五次交换位置后,小鼠所在的座号是3号;
第六次交换位置后,小鼠所在的座号是4号;
第七次交换位置后,小鼠所在的座号是2号;
第八次交换位置后,小鼠所在的座号是1号;
…,
所以小鼠的座号是3、4、2、1、3、4、2、1、…,每4个数一个循环,
因为2014÷4=503…2,
所以第2014次交换位置后,小鼠所在的座号是4号.
答:第2014次交换位置后,小鼠所在的座号是4号.
答案:D.
3.解:由分析可知,填表如下:
桌子/张 1 2 3 4 n
椅子/把 6 8 10 12 2n+4
1.0.234823482348…,这个纯循环小数的小数点后面第99位上的数字是( )
A.2 B.3 C.4 D.8
2.观察下列式子:0.2=123÷999,0.3=237÷999,0.4=45÷999,那么,0.5等于( )
A.0.45÷999 B.4.5÷999 C.45÷999 D.450÷999
3.一列分数的前4个是、、、.根据这4个分数的规律可知,第8个分数是( )
A. B. C. D.
4.21.78÷0.4=54.45
219.78÷0.4=549.45
2199.78÷0.4=5499.45……
按照上面的规律,下面正确的等式是( )
A.219999.78÷0.4=54999.45 B.2199.78÷0.4=54999.45
C.21999.78÷0.4=5499.945 D.219999.78÷0.4=549999.45
填在如图各正方形中的四个数之间都有相同的规律,根据此规律,m的值是( )
A.38 B.52 C.66 D.74
1.依据图中的规律,在括号里填上适当的分数。
2.先观察前面三道题,再填出横线里的数.
1×9+2=11,12×9+3=111,123×9+4=1111,1234×9+ = ,
×9+ =1111111.
3.奇妙的算式.
5×5=25
95×95=9025
995×995=990025
9995×9995=99900025
99995×99995= .
4.根据已有的结果找出规律,直接写得数.
6.6×6.7=44.22 66.666×66.667=
66.6×66.7=4442.22 666.666×666.667=
666.6×666.7=444422.22 6.666666×6666.667=
5.23.12.34,12.43,13.24,13.42,…,43.12,43.21,在这组数中,自左往右数,第19个数是多少?
1.将2化成循环小数是 ,小数点右边第2014位上的数字是 .
2.有一列数,第一个数是100,第二个数是90,从第三个数开始,每个数都是它前面两个数的平均数.第三十个数的整数部分是 .
3.一个同学暑假参加爬梯子闯关游戏,当他爬到梯子正中间时,二楼窗口喷出水来,他就往下退了3级,等到水过去了,他又爬了7级,这时屋顶有小沙包掉下来,他又往后退了2级,幸好没滑下,他又爬了8级,这时他距梯子最高层还有1级,问这个梯子共有 级.
4.按规律填数.
(1)2,5,8,11, , .
(2),,,, , .
(3),,,, , .
(4)
5.按规律填数.
(1)0.2、1.1、2.2、3.5、 、 .
(2)
1.桌上有1张纸,第一次把它剪成3块放回桌上;第二次从桌上拿起1块剪成3块后放回桌上;….进行了这样的8次操作后,桌上一共有( )块纸.
A.24 B.21 C.19 D.17
2.根据各式的规律填空:
1=12
1+3=22
1+3+5=32
1+3+5+7=42
(1)1+3+5+7+9+11+13= 2.(2)从1开始, 个连续奇数相加的和是202.
3.在生产和生活中,我们经常把一些同样大小的圆柱管捆扎起来,下面我们来探索捆扎一圈时绳子的长度.假设每个圆柱管的外直径都是10厘米,圆柱管的放置时“单层平放”,打结处绳子的长度不计,捆扎后横截面如下所示:
(1)探索:
个数 图形 绳子长度
1
厘米
2
厘米
3
厘米
… … …
(2)推想:
①当圆柱管的个数是10时,所用绳子的长度是 厘米.
②当圆柱管的个数是a时,所用绳子的长度是 厘米.
1.找规律,往下接着画.
2.如图,四个电子宠物排座位:一开始,小鼠、小猴、小兔、小猫分别坐在1、2、3、
4号的座位上,以后它们不停地交换位置,第一次上下两排交换位置,第二次是在第一次交换位置后,再左右两列交换位置,第三次是在第二次交换位置后,再上下两排交换位置,第四次是在第三次交换位置后,再左右两列交换位置,…这样一直继续交换位置,第2014次交换位置后,小鼠所在的座号是( )
A.1 B.2 C.3 D.4
3.探索规律,完成表格
桌子/张 1 2 3 4 n
椅子/把 6 8
参考答案及难题详解
第二十六关
1.解:0.234823482348…的循环节是2348,是4位数,
99÷4=24…3,从循环节的首位起第三位上的数字是4;
答案:C.
2.解:观察已知三个算式,当除数是999时,将被除数小数点向左移动3位,然后在十分位和千分位的数字上加上循环符号,就是算式的商,
所以,已知商为0.5,将循环符号去掉,然后小数点向右移动三位就是被除数,即
450,得到算式:0.5=450÷999 答案:D。
3.解:第8个数的分子是8;
由前4个分数是、、、可知,分子是1、2、3、4.
第n个分数的分子就是n,所以第8个数的分子是8;
分母是2,5,10、17,观察可知:?
2=1?+1,?5=2?+1, 10=3?+1,?17=4?+1,
则第n个分数的分母为n?+1,所以第8个分数的分母为8?+1=65,
即第8个分数是; 答案:C.
4.解:21.78÷0.4=54.45
219.78÷0.4=549.45
2199.78÷0.4=5499.45
……
219999.78÷0.4=549999.45
……
答案:D.
5..解:根据图形的规律,第4个图形:
左下应该是6+2=8
右上数字为:6+4=10
右下数字为:8×10﹣6=74
答:m的值是74.答案:D.
第二十七关
1.解:分子构成的数列为:3,5,7,9,11,13,……;
分母构成的规律用式子表示为:1+3=4,4+5=9,9+7=16,16+9=25,25+11=36,36+13=49,……。
故第6层的分数为
2.解:1×9+2=11,12×9+3=111,123×9+4=1111,1234×9+5=11111,123456×9+7=1111111;
答案:5,11111,123456,7。
3.解:认真观察5×5=25
95×95=9025
995×995=990025
9995×9995=99900025 得出规律,因数在5的前面有几个9,则在积中25的前面就有几个9和几个0,
所以,99995×99995=9999000025;
答案:9999000025.
4.解:根据已有的结果找出规律,直接写得数.
6.6×6.7=44.22 66.666×66.667=4444.422222
66.6×66.7=4442.22 666.666×666.667=444444.222222
666.6×666.7=444422.22 6.66666×6666.667=44444.442222222
5.解:12.34,12.43,13.24,13.42,…,43.12,43.21,是用1、2、3、4这四个数字和小数点组成的两位小数,然后把这些两位小数按照从小到大排列
一共有:4×3×2×1=24(个)
第24个是:43.21,第23个是:43.12,第22个是:34.21,第21个是:34.12,第20个是:24.31,第19个是:24.13.
答:第19个数是24.13.
第二十八关
1.解:2=2.1428
小数部分是7、1、4、2、8、5六个数字的循环小数,
2014÷6=335…4
余数是4,所以小数点右边第2014位上的数字是一个循环的第4个数字2;
答案:2.1428,2.
2.解:(100+90)÷2=95,(95+90)÷2=92.5,(95+92.5)÷2=93.75,(93.75+92.5)÷2=93,(93.5+93)÷2=93.25,(93.25+93)÷2=93.125,
前面两个数一定都是90多,其平均数一定也是90多,所以无论第几个整数部分都是93(除了第一组,第二 组);即从第五个数起每个数的整数部分是93.
答案:93.
3.解:设中间一级为第x级,则全梯共有2x﹣1级,根据题意得:
x﹣3+7﹣2+8+1=2x﹣1
x=12
2x﹣1=2×12﹣1=23.
答:这个梯子共有23级.
答案:23.
解:
(1)11+3=14, 14+3=17;
(2)=; =;
(3)分母:6×6=36, 分子:36﹣1=35,
这个分数是:;
分母:7×7=49, 分子:49﹣1=48,
这个分数是:.
(4)(58﹣10)÷6,
=48÷6,
=8;
所以是这个数列的第9项,它的分子就是10.即这个分数是.
5.(1)5、6.7.根据已知的数可得排列规律:从0.2开始每次递增0.9、1.1、1.3、1.5、1.7、1.9;据此解答。
(2)答案:20,22,24;50,45,40。
第二十九关
1.解:由以上分析可知,第八次操作后的块数是:
3+2×(8﹣1)=17(块) 答案:D.
2.(1)1+3+5+7+9+11+13=72;
(2)观察图形可知,从1开始的连续奇数的和等于奇数个数的平方,
所以从1开始,20个连续奇数相加的和是202.
答案:(1)7;(2)20.
3.解:①π×10=10π(厘米);②10π+20(厘米);
③10π+20×2=10π+40(厘米);
统计表如下:
个数 图形 绳子长度
1
10π厘米
2
10π+20厘米
3
10π+40厘米
… … …
(2)①当圆柱管的个数是10时,所用绳子的长度是:
10π+20×(10﹣1)=10π+180(厘米);
②当圆柱管的个数是a时,所用绳子的长度是:
10π+(a﹣1)×10×2
=10π+a×10﹣1×10×2
=10π+20a﹣20(厘米);
答案:10π+180;10π+20a﹣20.
第二十九关
1.
2.解:根据题意,可得
第一次交换位置后,小鼠所在的座号是3号;
第二次交换位置后,小鼠所在的座号是4号;
第三次交换位置后,小鼠所在的座号是2号;
第四次交换位置后,小鼠所在的座号是1号;
第五次交换位置后,小鼠所在的座号是3号;
第六次交换位置后,小鼠所在的座号是4号;
第七次交换位置后,小鼠所在的座号是2号;
第八次交换位置后,小鼠所在的座号是1号;
…,
所以小鼠的座号是3、4、2、1、3、4、2、1、…,每4个数一个循环,
因为2014÷4=503…2,
所以第2014次交换位置后,小鼠所在的座号是4号.
答:第2014次交换位置后,小鼠所在的座号是4号.
答案:D.
3.解:由分析可知,填表如下:
桌子/张 1 2 3 4 n
椅子/把 6 8 10 12 2n+4
同课章节目录
