(小升初真题专项)六年级数学找规律题(易错题、难题)名师详解连载三 (含答案)
文档属性
| 名称 | (小升初真题专项)六年级数学找规律题(易错题、难题)名师详解连载三 (含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 00:00:00 | ||
图片预览



文档简介
(小升初真题)六年级数学找规律题(易错题、难题)名师详解连载三
1.小强用小棒玩搭房子游戏(如下图),搭1间房用5根小棒,搭2间房用9根小棒.像这样搭3间房用( )根小棒,搭4间房用( )根小棒,搭n间房用( )根小棒。
4.下面的每一个图形都是由△、口、○中的两个组成的。观察各个图形,根据图形下面的数找出规律,画出表示“23”和“12”的图形。
2.观察思考。
上面每个图形都是由边长为1 cm的正方形拼成的,请仔细观察,并填表。
第个图形 ① ② ③ ④ ⑤ …
面积/cm2 1 3 6
…
周长/cm 4 8 12
…
1.有黄、红、绿、蓝、紫五种颜色的花,每两种颜色的花为一组,最多可以配成不重复的( )组。
2.用黑白两种颜色的正方形纸片,按黑色纸片逐渐加1的规律拼成一列图案(如下图):
(1)第4个图案中白色纸片有( )张; (2)第n个图案中白色纸片有(? )张。
分割次数 1 2 3 4 5 …
正方形总个数 4 7 10
…
3.一个正方形和一个三角形可以组合成一个不规则的五边形,如图所示:下列每个五边形的面积随着三角形高度的加倍而增加,其中每个五边形中正方形的边长为20厘米,三角形的高分别为5厘米、10厘米、20厘米、40厘米,按照这一模式,第6个五边形的面积是多少平方厘米?
分割次数 1 2 3 4 5 …
正方形总个数 4 7 10
…
分割次数 1 2 3 4 5 …
正方形总个数 4 7 10
…
5.小明在一条长凳上做摆卡片的游戏,如下图,他用三种摆法都正好从长凳的一端摆到另一端而没有剩余(第三种摆法中最后一个长方形是横向摆放的)。已知卡片长18厘米,宽12厘米,板凳最短是( )厘米。
A.36 B.72 C.180 D.360
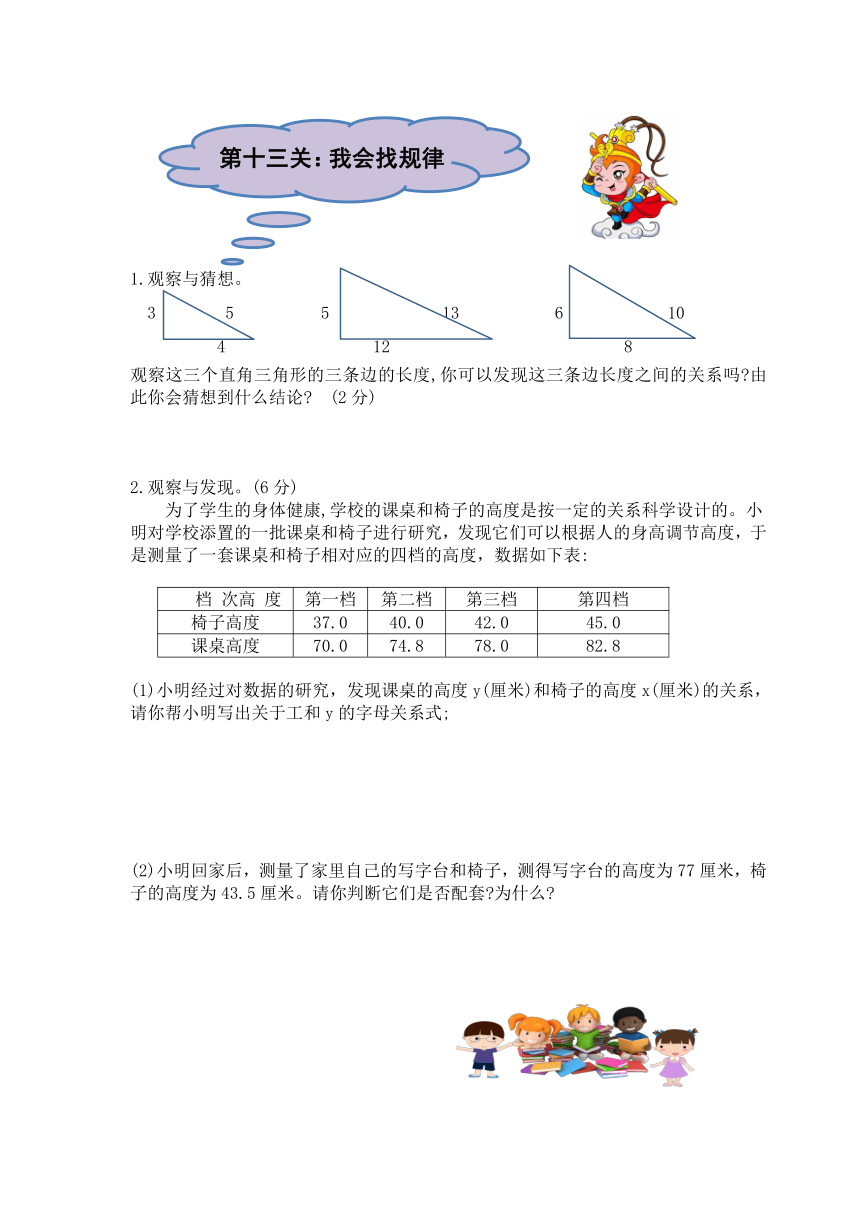
1.观察与猜想。
3 5 5 13 6 10
4 12 8
观察这三个直角三角形的三条边的长度,你可以发现这三条边长度之间的关系吗?由此你会猜想到什么结论??(2分)
2.观察与发现。(6分)
为了学生的身体健康,学校的课桌和椅子的高度是按一定的关系科学设计的。小
明对学校添置的一批课桌和椅子进行研究,发现它们可以根据人的身高调节高度,于是测量了一套课桌和椅子相对应的四档的高度,数据如下表:
档 次高 度 第一档 第二档 第三档 第四档
椅子高度 37.0 40.0 42.0 45.0
课桌高度 70.0 74.8 78.0 82.8
档 次高 度 第一档 第二档 第三档 第四档
椅子高度 37.0 40.0 42.0 45.0
课桌高度 70.0 74.8 78.0 82.8
档 次高 度 第一档 第二档 第三档 第四档
椅子高度 37.0 40.0 42.0 45.0
课桌高度 70.0 74.8 78.0 82.8
(1)小明经过对数据的研究,发现课桌的高度y(厘米)和椅子的高度x(厘米)的关系,请你帮小明写出关于工和y的字母关系式;
(2)小明回家后,测量了家里自己的写字台和椅子,测得写字台的高度为77厘米,椅子的高度为43.5厘米。请你判断它们是否配套?为什么?
图①.②.③.④都是平面图形。
(1)数一数每个图形各有多少个顶点,多少条边,这些边围出了多少个区城,将结果填人下表中(其中①已填好)。
图形 顶点数 边数 区域数
① 4 6 3
② ? ? ?
③ ? ? ?
④ ? ? ?
(2)观察上表,推断一个平面图形的顶点数、边数、区域数之间的关系。
(3)现已知某一平面图形有999个顶点和999个区城,试根据(2)中推断出的关系,确定这个图形有多少条边。
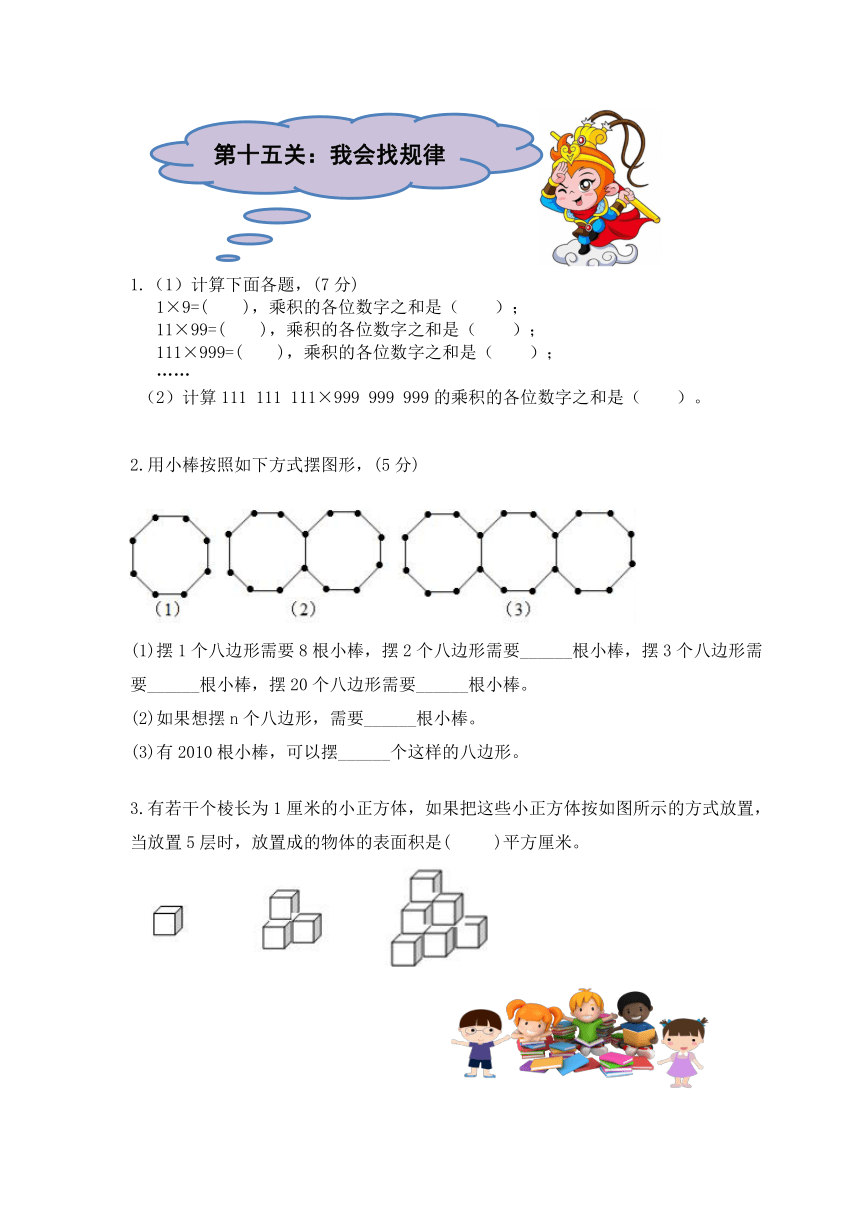
1.(1)计算下面各题,(7分)
1×9=( ),乘积的各位数字之和是( );
11×99=( ),乘积的各位数字之和是( );
111×999=( ),乘积的各位数字之和是( );
……
(2)计算111 111 111×999 999 999的乘积的各位数字之和是( )。
2.用小棒按照如下方式摆图形,(5分)
(1)摆1个八边形需要8根小棒,摆2个八边形需要______根小棒,摆3个八边形需要______根小棒,摆20个八边形需要______根小棒。
(2)如果想摆n个八边形,需要______根小棒。
(3)有2010根小棒,可以摆______个这样的八边形。
3.有若干个棱长为1厘米的小正方体,如果把这些小正方体按如图所示的方式放置,当放置5层时,放置成的物体的表面积是( )平方厘米。
参考答案及难题详解
第十一关
1.
解答
搭1间房用5根小棒
搭2间房用9根小棒
搭3间房用小棒:?5+4+4=13?(根)
搭4间房需要小棒:?5+4+4+4=17?(根)
搭n间房需要小棒:?5+4(n-1)=(4n+1)根
答:搭3间房用13根小棒,搭4间房用17根小棒,搭n间房用(4n+1)根小棒
故答案为:?13;?17;?(4n+1)
解析
根据图示可知:搭1间房用5根小棒,搭2间房用9根小棒,搭3间房用小棒:
5+4+4=13(根),?搭4间房需要小棒:5+4+4+4=17(根)……
搭n间房需要小棒:5+4(n-1)=(4n+1)根.据此解得。
2.
[解析]本题考查根据图形与数的规律画图。观察给出的图形和对应的数,可以发现外层的图形表示十位上的数,里层的图形表示个位上的数,△代表1,□代表3,○代表2。所以23表示的图形外层是○,内层是口,为 ;12表示的图形外层是△,内层是○,为 。
3.
第十二关
1.10
解析
此题考查了排列组合中的组合问题.对于这个简单问题,可以全部列出,数数即可得?解可以根据线段的计数来解答,共有n个顶点,则共有1+2+3+…+(n-1)条线段,据此把颜色的种类看做端点的个数解答即可.
解答
4+3+2+1=10(组) 答:可以分为10组.
2.(1)13?(2)3n+1
解析
观察题干可得:第1个图案中有白色纸片3×1+1张,第2个图案中有白色纸片3×2+1张,第3个图案中有白色纸片3×3+1张,第4个图案中有白色纸片3×4+1=13张,第5个图案中有白色纸片3×5+1……第n个图案中有白色纸片3n+1张由此解答。
详解:由规律得:
(1)第4个图案中有白色纸片:
3×4+1=13(张)
(2)第n个图案中有白色纸片3n+1张;故答案为:13;?3n+1.
3.解:
根据题意可得五边形中的三角形的高有这样一个规律: 相邻两个三角形,后一个的高是前一个高的2倍。
所以按照这一模式第6个五边形中三角形的高为160厘米
因为正方形的边长为20厘米,第6个五边形中三角形的高为160厘米
所以第6个五边形的面积
=20×20+×20×160=200平方厘米
4.C 18、12、30的最小公倍数是180
第十三关
1.3?+4?=5??5?+12?=13??6?+8?=10?
结论:在直角三角形中,两条直角边长度的平方和等于斜边长度的平方。
2.
(1)设桌高y与凳高x的关系为y=kx?+b(k:≠0),依题意得:
70=37k+b
74.8=40k+b
解得k=1.6b=10.8
:.桌高y与凳高x的关系式为y=1.6x+10.8;
(2)不配套,理由如下:
当x=43.5时,y=1.6×43.5+10.8=80.4? 80.4≠77,所以不配套
第十四关
1.(1)
图形 顶点数 边数 区域数
① 4 6 3
② 8 12 5
③ 6 9 4
④ 10 15 6
(2)顶点数+区域数-边数=1
(3)?999+999-1=1997(条)
第十五关
(1)9 9 1089 18 110889 27 (2)81
解析:
(1)由题意得:观察题目,然后通过计算会发现:1×9=(9),乘积的各位数字之和是(9);?因数是1个9
11×99=(1089),乘积的各位数字之和是(18);因数是2个9
111×999=(110889),乘积的各位数字之和是(27);因数是3个9
那么就有:?1111×9999=(111088899),乘积的各位数字之和是(36);因数是4个9就可以计算(2)
(2)计算:111 111 111×999 999 999.这个乘积的各位数字之和是多少?因数是9个9,那么它的和是81
2.(1)15?22?141?(2)?7n+1?(3)287?
解析:
摆一个八边形用了8根小棒,摆两个八边形就多用了7根,摆三个就多用了7×2根,……能够根据图形发现规律:多一个八边形,就多用7根小棒,则摆n个八边形,需要小棒:?8+7(n-1)?=7n+1根
详解:根据题干分析可得:摆一个八边形用了8根小棒,摆两个八边形需要8+7=15(根),摆三个需要8+7×2=22(根),所以摆a个八边形,需要小棒8+7(a-1)=7a+1根,当a=20时,7×20+1=141(根),当7a+1=2010时,7a=2009,
a=287,故答案为:?15;?22;?141;?7a+1;?287.
3.90
分析:
观察发现,1层时,表面积是6×1,2层时,表面积是6×(1+2),3层时时,表面积时表面积是6×(1+2+3),所以5层时,表面积是6×(1+2+3+4+5),n层时,表面积是6×(1+2+3+…+n),据此解答即可.
解答:
3层时,6×(1+2+3)=36(平方厘米),
5层时,6×(1+2+3+4+5)=90(平方厘米),
n层时,6×(1+2+3+…+n)=3n?+3n(平方厘米).
n=6,3n?+3n=3×5?+3×5=90
答:当有3层时,这个立方体图形的表面积是36平方厘米,当有5层时,这个立方体图形的表面积是90平方厘米,n层时,这个立方体图形的表面积是3n?+3n平方厘米。
1.小强用小棒玩搭房子游戏(如下图),搭1间房用5根小棒,搭2间房用9根小棒.像这样搭3间房用( )根小棒,搭4间房用( )根小棒,搭n间房用( )根小棒。
4.下面的每一个图形都是由△、口、○中的两个组成的。观察各个图形,根据图形下面的数找出规律,画出表示“23”和“12”的图形。
2.观察思考。
上面每个图形都是由边长为1 cm的正方形拼成的,请仔细观察,并填表。
第个图形 ① ② ③ ④ ⑤ …
面积/cm2 1 3 6
…
周长/cm 4 8 12
…
1.有黄、红、绿、蓝、紫五种颜色的花,每两种颜色的花为一组,最多可以配成不重复的( )组。
2.用黑白两种颜色的正方形纸片,按黑色纸片逐渐加1的规律拼成一列图案(如下图):
(1)第4个图案中白色纸片有( )张; (2)第n个图案中白色纸片有(? )张。
分割次数 1 2 3 4 5 …
正方形总个数 4 7 10
…
3.一个正方形和一个三角形可以组合成一个不规则的五边形,如图所示:下列每个五边形的面积随着三角形高度的加倍而增加,其中每个五边形中正方形的边长为20厘米,三角形的高分别为5厘米、10厘米、20厘米、40厘米,按照这一模式,第6个五边形的面积是多少平方厘米?
分割次数 1 2 3 4 5 …
正方形总个数 4 7 10
…
分割次数 1 2 3 4 5 …
正方形总个数 4 7 10
…
5.小明在一条长凳上做摆卡片的游戏,如下图,他用三种摆法都正好从长凳的一端摆到另一端而没有剩余(第三种摆法中最后一个长方形是横向摆放的)。已知卡片长18厘米,宽12厘米,板凳最短是( )厘米。
A.36 B.72 C.180 D.360
1.观察与猜想。
3 5 5 13 6 10
4 12 8
观察这三个直角三角形的三条边的长度,你可以发现这三条边长度之间的关系吗?由此你会猜想到什么结论??(2分)
2.观察与发现。(6分)
为了学生的身体健康,学校的课桌和椅子的高度是按一定的关系科学设计的。小
明对学校添置的一批课桌和椅子进行研究,发现它们可以根据人的身高调节高度,于是测量了一套课桌和椅子相对应的四档的高度,数据如下表:
档 次高 度 第一档 第二档 第三档 第四档
椅子高度 37.0 40.0 42.0 45.0
课桌高度 70.0 74.8 78.0 82.8
档 次高 度 第一档 第二档 第三档 第四档
椅子高度 37.0 40.0 42.0 45.0
课桌高度 70.0 74.8 78.0 82.8
档 次高 度 第一档 第二档 第三档 第四档
椅子高度 37.0 40.0 42.0 45.0
课桌高度 70.0 74.8 78.0 82.8
(1)小明经过对数据的研究,发现课桌的高度y(厘米)和椅子的高度x(厘米)的关系,请你帮小明写出关于工和y的字母关系式;
(2)小明回家后,测量了家里自己的写字台和椅子,测得写字台的高度为77厘米,椅子的高度为43.5厘米。请你判断它们是否配套?为什么?
图①.②.③.④都是平面图形。
(1)数一数每个图形各有多少个顶点,多少条边,这些边围出了多少个区城,将结果填人下表中(其中①已填好)。
图形 顶点数 边数 区域数
① 4 6 3
② ? ? ?
③ ? ? ?
④ ? ? ?
(2)观察上表,推断一个平面图形的顶点数、边数、区域数之间的关系。
(3)现已知某一平面图形有999个顶点和999个区城,试根据(2)中推断出的关系,确定这个图形有多少条边。
1.(1)计算下面各题,(7分)
1×9=( ),乘积的各位数字之和是( );
11×99=( ),乘积的各位数字之和是( );
111×999=( ),乘积的各位数字之和是( );
……
(2)计算111 111 111×999 999 999的乘积的各位数字之和是( )。
2.用小棒按照如下方式摆图形,(5分)
(1)摆1个八边形需要8根小棒,摆2个八边形需要______根小棒,摆3个八边形需要______根小棒,摆20个八边形需要______根小棒。
(2)如果想摆n个八边形,需要______根小棒。
(3)有2010根小棒,可以摆______个这样的八边形。
3.有若干个棱长为1厘米的小正方体,如果把这些小正方体按如图所示的方式放置,当放置5层时,放置成的物体的表面积是( )平方厘米。
参考答案及难题详解
第十一关
1.
解答
搭1间房用5根小棒
搭2间房用9根小棒
搭3间房用小棒:?5+4+4=13?(根)
搭4间房需要小棒:?5+4+4+4=17?(根)
搭n间房需要小棒:?5+4(n-1)=(4n+1)根
答:搭3间房用13根小棒,搭4间房用17根小棒,搭n间房用(4n+1)根小棒
故答案为:?13;?17;?(4n+1)
解析
根据图示可知:搭1间房用5根小棒,搭2间房用9根小棒,搭3间房用小棒:
5+4+4=13(根),?搭4间房需要小棒:5+4+4+4=17(根)……
搭n间房需要小棒:5+4(n-1)=(4n+1)根.据此解得。
2.
[解析]本题考查根据图形与数的规律画图。观察给出的图形和对应的数,可以发现外层的图形表示十位上的数,里层的图形表示个位上的数,△代表1,□代表3,○代表2。所以23表示的图形外层是○,内层是口,为 ;12表示的图形外层是△,内层是○,为 。
3.
第十二关
1.10
解析
此题考查了排列组合中的组合问题.对于这个简单问题,可以全部列出,数数即可得?解可以根据线段的计数来解答,共有n个顶点,则共有1+2+3+…+(n-1)条线段,据此把颜色的种类看做端点的个数解答即可.
解答
4+3+2+1=10(组) 答:可以分为10组.
2.(1)13?(2)3n+1
解析
观察题干可得:第1个图案中有白色纸片3×1+1张,第2个图案中有白色纸片3×2+1张,第3个图案中有白色纸片3×3+1张,第4个图案中有白色纸片3×4+1=13张,第5个图案中有白色纸片3×5+1……第n个图案中有白色纸片3n+1张由此解答。
详解:由规律得:
(1)第4个图案中有白色纸片:
3×4+1=13(张)
(2)第n个图案中有白色纸片3n+1张;故答案为:13;?3n+1.
3.解:
根据题意可得五边形中的三角形的高有这样一个规律: 相邻两个三角形,后一个的高是前一个高的2倍。
所以按照这一模式第6个五边形中三角形的高为160厘米
因为正方形的边长为20厘米,第6个五边形中三角形的高为160厘米
所以第6个五边形的面积
=20×20+×20×160=200平方厘米
4.C 18、12、30的最小公倍数是180
第十三关
1.3?+4?=5??5?+12?=13??6?+8?=10?
结论:在直角三角形中,两条直角边长度的平方和等于斜边长度的平方。
2.
(1)设桌高y与凳高x的关系为y=kx?+b(k:≠0),依题意得:
70=37k+b
74.8=40k+b
解得k=1.6b=10.8
:.桌高y与凳高x的关系式为y=1.6x+10.8;
(2)不配套,理由如下:
当x=43.5时,y=1.6×43.5+10.8=80.4? 80.4≠77,所以不配套
第十四关
1.(1)
图形 顶点数 边数 区域数
① 4 6 3
② 8 12 5
③ 6 9 4
④ 10 15 6
(2)顶点数+区域数-边数=1
(3)?999+999-1=1997(条)
第十五关
(1)9 9 1089 18 110889 27 (2)81
解析:
(1)由题意得:观察题目,然后通过计算会发现:1×9=(9),乘积的各位数字之和是(9);?因数是1个9
11×99=(1089),乘积的各位数字之和是(18);因数是2个9
111×999=(110889),乘积的各位数字之和是(27);因数是3个9
那么就有:?1111×9999=(111088899),乘积的各位数字之和是(36);因数是4个9就可以计算(2)
(2)计算:111 111 111×999 999 999.这个乘积的各位数字之和是多少?因数是9个9,那么它的和是81
2.(1)15?22?141?(2)?7n+1?(3)287?
解析:
摆一个八边形用了8根小棒,摆两个八边形就多用了7根,摆三个就多用了7×2根,……能够根据图形发现规律:多一个八边形,就多用7根小棒,则摆n个八边形,需要小棒:?8+7(n-1)?=7n+1根
详解:根据题干分析可得:摆一个八边形用了8根小棒,摆两个八边形需要8+7=15(根),摆三个需要8+7×2=22(根),所以摆a个八边形,需要小棒8+7(a-1)=7a+1根,当a=20时,7×20+1=141(根),当7a+1=2010时,7a=2009,
a=287,故答案为:?15;?22;?141;?7a+1;?287.
3.90
分析:
观察发现,1层时,表面积是6×1,2层时,表面积是6×(1+2),3层时时,表面积时表面积是6×(1+2+3),所以5层时,表面积是6×(1+2+3+4+5),n层时,表面积是6×(1+2+3+…+n),据此解答即可.
解答:
3层时,6×(1+2+3)=36(平方厘米),
5层时,6×(1+2+3+4+5)=90(平方厘米),
n层时,6×(1+2+3+…+n)=3n?+3n(平方厘米).
n=6,3n?+3n=3×5?+3×5=90
答:当有3层时,这个立方体图形的表面积是36平方厘米,当有5层时,这个立方体图形的表面积是90平方厘米,n层时,这个立方体图形的表面积是3n?+3n平方厘米。
同课章节目录
