(小升初真题专项)六年级数学操作题(易错题、难题)名师详解连载五(含答案)
文档属性
| 名称 | (小升初真题专项)六年级数学操作题(易错题、难题)名师详解连载五(含答案) | 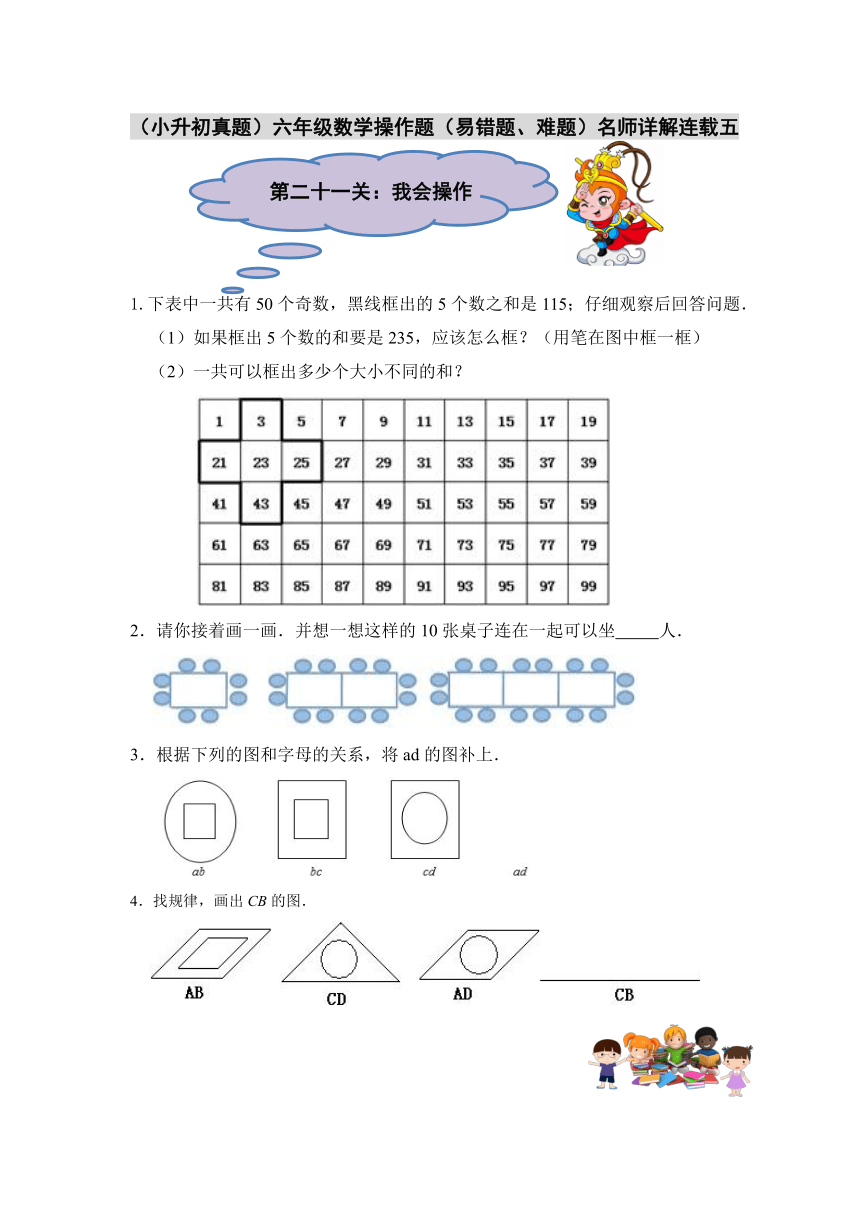 | |
| 格式 | doc | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 14:59:51 | ||
图片预览


文档简介
(小升初真题)六年级数学操作题(易错题、难题)名师详解连载五
1.下表中一共有50个奇数,黑线框出的5个数之和是115;仔细观察后回答问题.
(1)如果框出5个数的和要是235,应该怎么框?(用笔在图中框一框)
(2)一共可以框出多少个大小不同的和?
2.请你接着画一画.并想一想这样的10张桌子连在一起可以坐
人.
3.根据下列的图和字母的关系,将ad的图补上.
4.找规律,画出CB的图.
1.仔细观察,第四幅图应画什么图形?
2.如图,甲、乙、丙、丁四个图都称作平面图,观察图甲和表中对应数值,探究计数的方法并作答.
(1)数一数每个图各有多少个顶点,多少条边,这些边围出多少区域,并将结果填入下表.
图
甲
乙
丙
丁
顶点数m
4
7
边数n
6
9
区域数f
3
(2)根据表中数值,写出平面图的顶点数m,边数n、区域数f之间的一种关系:
。
(3)如果一个平面图有20个顶点和11个区域,那么利用(2)题中得出的关系,则这个平面图有
条边.
如图,数学实验室的窗户设计如图所示,如果每个符号代表一个数字,它们是837,571,206,439.求2018的图如何画?
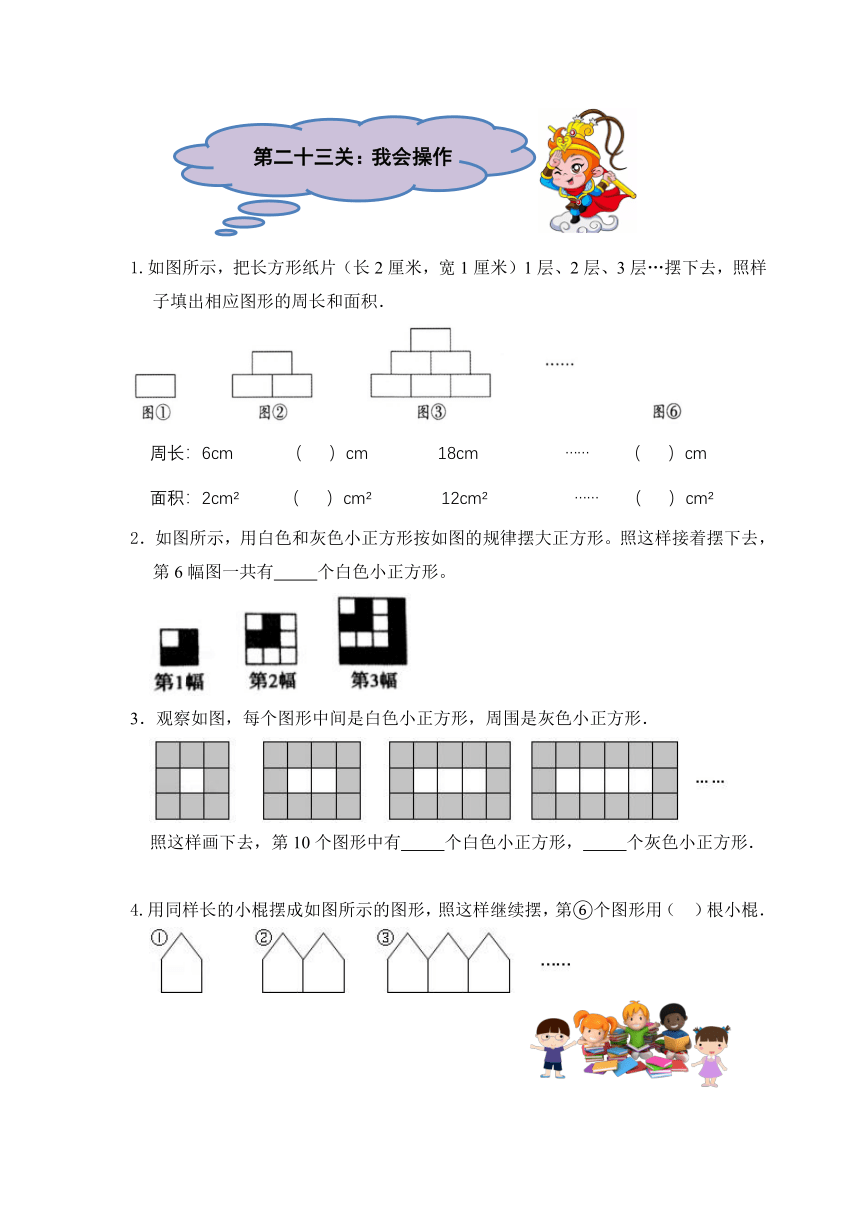
1.如图所示,把长方形纸片(长2厘米,宽1厘米)1层、2层、3层…摆下去,照样子填出相应图形的周长和面积.
周长:6cm
(
)cm
18cm
……
(
)cm
面积:2cm?
(
)cm?
12cm?
……
(
)cm?
2.如图所示,用白色和灰色小正方形按如图的规律摆大正方形。照这样接着摆下去,第6幅图一共有
个白色小正方形。
3.观察如图,每个图形中间是白色小正方形,周围是灰色小正方形.
照这样画下去,第10个图形中有
个白色小正方形,
个灰色小正方形.
4.用同样长的小棍摆成如图所示的图形,照这样继续摆,第⑥个图形用(
)根小棍.
1.摆1个正方形需要4根小棒,往后每多摆1个正方形就增加3根小棒,按这样的规律摆10个正方形,一共需要(
)根小棒.
2.教室里按2红1黄1蓝的顺序挂彩灯,共挂37盏.其中,红灯需挂(
)盏,黄灯需挂(
)盏,蓝灯需挂(
)盏.
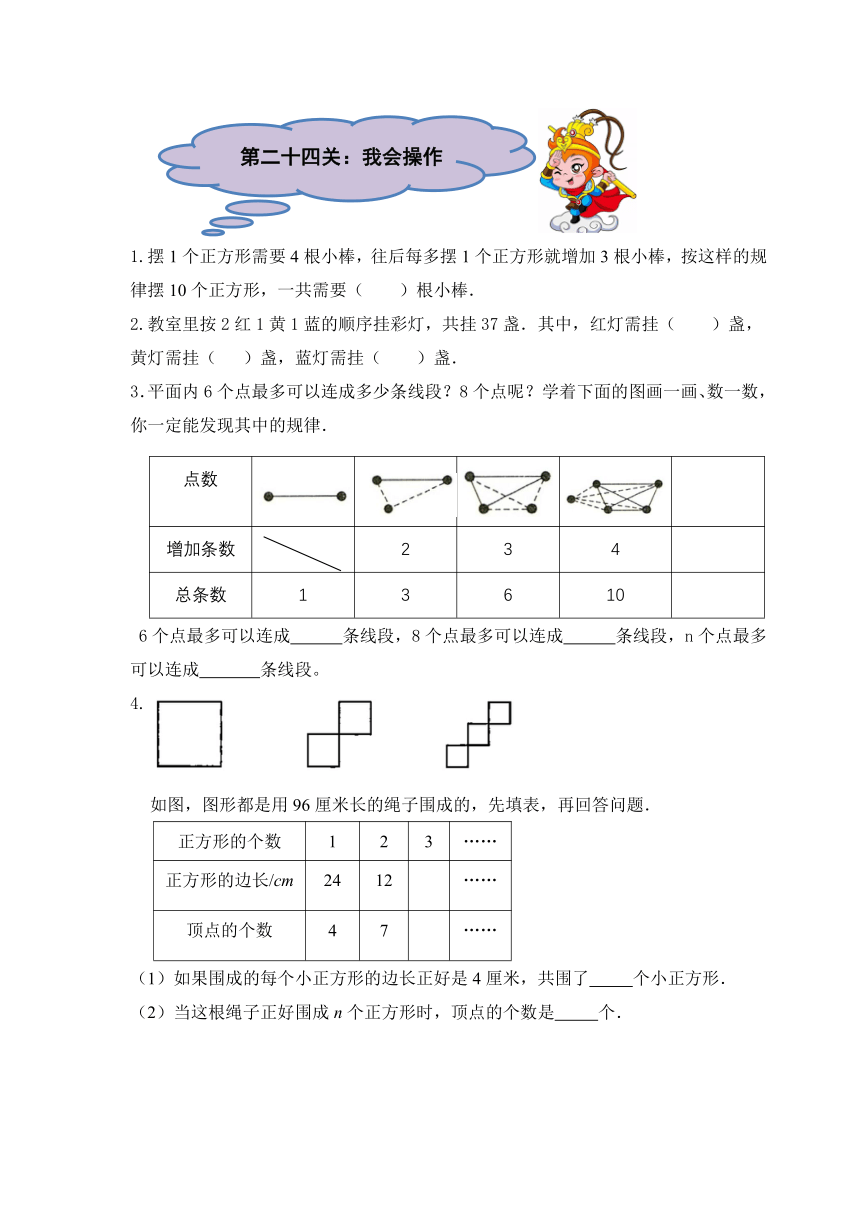
3.平面内6个点最多可以连成多少条线段?8个点呢?学着下面的图画一画、数一数,你一定能发现其中的规律.
点数
增加条数
2
3
4
总条数
1
3
6
10
6个点最多可以连成
条线段,8个点最多可以连成
条线段,n个点最多可以连成
条线段。
4.
如图,图形都是用96厘米长的绳子围成的,先填表,再回答问题.
正方形的个数
1
2
3
……
正方形的边长/cm
24
12
……
顶点的个数
4
7
……
(1)如果围成的每个小正方形的边长正好是4厘米,共围了
个小正方形.
(2)当这根绳子正好围成n个正方形时,顶点的个数是
个.
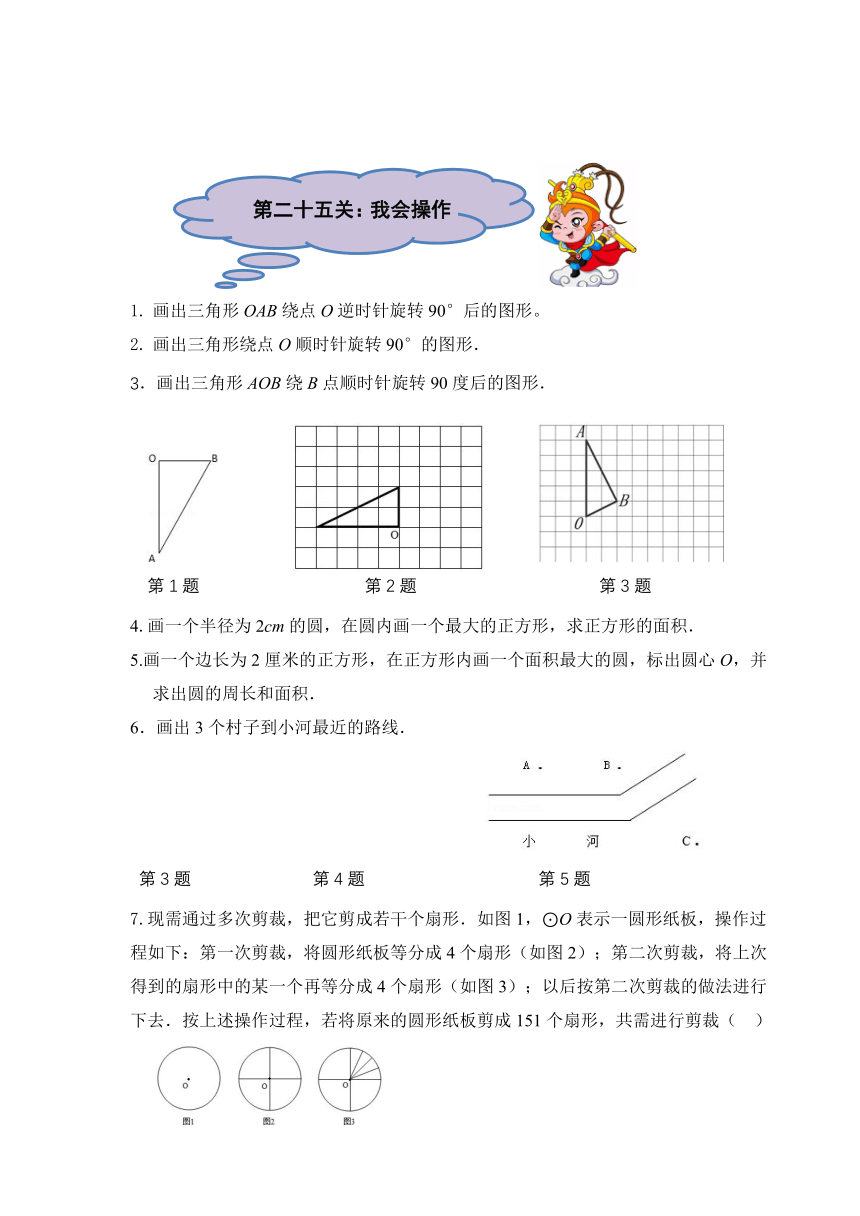
画出三角形OAB绕点O逆时针旋转90°后的图形。
画出三角形绕点O顺时针旋转90°的图形.
3.画出三角形AOB绕B点顺时针旋转90度后的图形.
第1题
第2题
第3题
4.画一个半径为2cm的圆,在圆内画一个最大的正方形,求正方形的面积.
5.画一个边长为2厘米的正方形,在正方形内画一个面积最大的圆,标出圆心O,并求出圆的周长和面积.
6.画出3个村子到小河最近的路线.
第3题
第4题
第5题
7.现需通过多次剪裁,把它剪成若干个扇形.如图1,⊙O表示一圆形纸板,操作过
程如下:第一次剪裁,将圆形纸板等分成4个扇形(如图2);第二次剪裁,将上次得到的扇形中的某一个再等分成4个扇形(如图3);以后按第二次剪裁的做法进行下去.按上述操作过程,若将原来的圆形纸板剪成151个扇形,共需进行剪裁(
)
参考答案及难题详解
第二十一关
1.解:根据规律框出的5个数的和是中间数的5倍可得:中间数是235÷5=45,其它四个数:45上面是25,下面65,左边是43,右边是47,框法如下:
(2)8×3=24(个);
答:一共可以框出24个大小不同的和.
2.解:由图示,摆放1张,2张,3张,…桌子,放的椅子数依次是8,12,16,…
8=4×1+4
12=4×2+4
16=4×3+4
那么,摆放n张餐桌应放的椅子数为:4n+4.
当n=10时,4×10+4
=40+4
=44(人)
答:10张桌子可以坐44人.
4.
第二十二关
1.
2.解:(1)结和图形我们可以得出:
图①有4个顶点、6条边、这些边围成3个区域;
图②有7个顶点、9条边、这些边围成3个区域;
图③有8个顶点、12条边、这些边围成5个区域;
图④有10个顶点、15条边、这些边围成6区域.
(2)根据以上数据,顶点用m表示,边数用n表
示,区域用f表示,他们的关系可表示为:m+f=n+1;
(3)把m=20,f=11代入上式得:n=m+f﹣1=20+11﹣1=30.
故如果平面图形有20个顶点和11个区域,那么这个平面图形的边数为30.
答案:m+f=n+1;30.
3.解:由图案和提供的数据可知:837,439第2位都是3,所以只有第2行和第4行是这两个数,第2行和第4行的末尾数字图形是7或者9,而571是其中一个数,第1行和第3行只有第一行的第2个图形是前面的那个7或9,所以第1行的数字是571,第2行是439,第3行是206,第4行是837;
即0,1,2,3,4,5,6,7,8,9分别用符号:
2018是:
第二十三关
1、12,6;36,42.
2×6=12(cm);6×6=36(cm);
2×3=6(cm?);(1+2+3+4+5+6)×2=42(cm?);
解:由图可知:
第1幅:?1个白色小正方形,
第2幅:?6个白色小正方形(1+5),
第3幅:?6个白色小正方形,
按如图规律:
第4幅:?15个白色小正方形(1+5+9),第5幅:15个白色小正方形,
第6幅:?1+5+9+13=28个白色小正方形.故答案为:?28.
3.解:第一个图形白色小正方形的个数为1个,灰色小正方形的个数为6+2=8(个)
第二个图形白色小正方形的个数为:2个,灰色小正方形的个数为:6+2+2=10(个)
……
第n个图形的白色小正方形的个数为n个,灰色小正方形的个数为(6+2n)个
所以第10个图形白色小正方形的个数为:10个
灰色小正方形的个数为:6+2×10=26(个)
答:第10个图形中有10个白色小正方形,26个灰色小正方形.
答案:10;26.
4.解:由图可知:
图形标号①的小棍根数为5;
图形标号②的小棍根数为9;
图形标号③的小棍根数为13;
…
由该搭建方式可得出规律:图形标号每增加1,小棍的个数增加4,
所以可以得出规律:搭第⑥个图形需要小棍根数为:6×4+1=25(根)
第二十四关
1..解:摆一个正方形要小棒4根;
摆两个正方形要小棒(4+3)根,即7根;
摆三个正方形要小棒(4+3×2)根,即10根,
…,
所以摆n个正方形要小棒:4+3×(n﹣1)=3n+1(根);
n=10,3×10+1=31(根);
答:摆10个正方形一共需要31根小棒.
2.解:37÷4=9…1
9个周期余1盏,则是红灯,
红灯数:2×9+1=19(盏)
黄灯数和蓝灯数都是1×9=9(盏)
3.解:根据题意,n个点的线段数是:1+2+3+4…+n﹣1条线段.
6个点可画:1+2+3+4+5=15(条)
8个点可画:1+2+3+4+5+6+7=28(条)
答:6个点,一共可以连15条线段;8个点,一共可以连28条线段.
4.分析;
根据图意,先计算出大正方形的边长;第几幅图就有几个小正方形,大正方形的边长就被平均分成了几份,每增加一个小正方形就增加3个顶点;据此完成表格,再根据表格进行解答即可.
解:96÷4=24(厘米)
24÷3=8(厘米)
4+3+3=10(个)
正方形的个数
1
2
3
……
正方形的边长/cm
24
12
8
……
顶点的个数
4
7
10
……
(1)24÷4=6(个)
答:如果围成的每个小正方形的边长正好是4厘米,共围了6个小正方形.
(2)4+3(n﹣1)=3n+1(个)
答:当这根绳子正好围成n个正方形时,顶点的个数是(3n+1)个.
答案:6;(3n+1).
第二十五关
1.解:画出三角形OAB绕点O逆时针旋转90°后的图形(图中红色部分):
2.解:画出三角形绕点O顺时针旋转90°的图形(图中红色部分:
3.
4.解:作图如下:
2r×r÷2×2
=2r×r
=2×2×2
=8(平方厘米).
答:正方形的面积是8平方厘米.
5.解:在正方形内画一个面积最大的圆,标出圆心O(下图):
3.14×2=6.28(厘米)
3.14×()2
=3.14×1
=3.14(平方厘米)
答:这个圆的周长是6.28厘米,面积是3.14平方厘米.
6.
7.解:设共需剪裁n次:
3n+1=151,
n=50;
剪成151个扇形需要剪50次;答案:B.
第二十一关:我会操作
第二十二关:我会操作
第二十三关:我会操作
第二十四关:我会操作
第二十五关:我会操作
1.下表中一共有50个奇数,黑线框出的5个数之和是115;仔细观察后回答问题.
(1)如果框出5个数的和要是235,应该怎么框?(用笔在图中框一框)
(2)一共可以框出多少个大小不同的和?
2.请你接着画一画.并想一想这样的10张桌子连在一起可以坐
人.
3.根据下列的图和字母的关系,将ad的图补上.
4.找规律,画出CB的图.
1.仔细观察,第四幅图应画什么图形?
2.如图,甲、乙、丙、丁四个图都称作平面图,观察图甲和表中对应数值,探究计数的方法并作答.
(1)数一数每个图各有多少个顶点,多少条边,这些边围出多少区域,并将结果填入下表.
图
甲
乙
丙
丁
顶点数m
4
7
边数n
6
9
区域数f
3
(2)根据表中数值,写出平面图的顶点数m,边数n、区域数f之间的一种关系:
。
(3)如果一个平面图有20个顶点和11个区域,那么利用(2)题中得出的关系,则这个平面图有
条边.
如图,数学实验室的窗户设计如图所示,如果每个符号代表一个数字,它们是837,571,206,439.求2018的图如何画?
1.如图所示,把长方形纸片(长2厘米,宽1厘米)1层、2层、3层…摆下去,照样子填出相应图形的周长和面积.
周长:6cm
(
)cm
18cm
……
(
)cm
面积:2cm?
(
)cm?
12cm?
……
(
)cm?
2.如图所示,用白色和灰色小正方形按如图的规律摆大正方形。照这样接着摆下去,第6幅图一共有
个白色小正方形。
3.观察如图,每个图形中间是白色小正方形,周围是灰色小正方形.
照这样画下去,第10个图形中有
个白色小正方形,
个灰色小正方形.
4.用同样长的小棍摆成如图所示的图形,照这样继续摆,第⑥个图形用(
)根小棍.
1.摆1个正方形需要4根小棒,往后每多摆1个正方形就增加3根小棒,按这样的规律摆10个正方形,一共需要(
)根小棒.
2.教室里按2红1黄1蓝的顺序挂彩灯,共挂37盏.其中,红灯需挂(
)盏,黄灯需挂(
)盏,蓝灯需挂(
)盏.
3.平面内6个点最多可以连成多少条线段?8个点呢?学着下面的图画一画、数一数,你一定能发现其中的规律.
点数
增加条数
2
3
4
总条数
1
3
6
10
6个点最多可以连成
条线段,8个点最多可以连成
条线段,n个点最多可以连成
条线段。
4.
如图,图形都是用96厘米长的绳子围成的,先填表,再回答问题.
正方形的个数
1
2
3
……
正方形的边长/cm
24
12
……
顶点的个数
4
7
……
(1)如果围成的每个小正方形的边长正好是4厘米,共围了
个小正方形.
(2)当这根绳子正好围成n个正方形时,顶点的个数是
个.
画出三角形OAB绕点O逆时针旋转90°后的图形。
画出三角形绕点O顺时针旋转90°的图形.
3.画出三角形AOB绕B点顺时针旋转90度后的图形.
第1题
第2题
第3题
4.画一个半径为2cm的圆,在圆内画一个最大的正方形,求正方形的面积.
5.画一个边长为2厘米的正方形,在正方形内画一个面积最大的圆,标出圆心O,并求出圆的周长和面积.
6.画出3个村子到小河最近的路线.
第3题
第4题
第5题
7.现需通过多次剪裁,把它剪成若干个扇形.如图1,⊙O表示一圆形纸板,操作过
程如下:第一次剪裁,将圆形纸板等分成4个扇形(如图2);第二次剪裁,将上次得到的扇形中的某一个再等分成4个扇形(如图3);以后按第二次剪裁的做法进行下去.按上述操作过程,若将原来的圆形纸板剪成151个扇形,共需进行剪裁(
)
参考答案及难题详解
第二十一关
1.解:根据规律框出的5个数的和是中间数的5倍可得:中间数是235÷5=45,其它四个数:45上面是25,下面65,左边是43,右边是47,框法如下:
(2)8×3=24(个);
答:一共可以框出24个大小不同的和.
2.解:由图示,摆放1张,2张,3张,…桌子,放的椅子数依次是8,12,16,…
8=4×1+4
12=4×2+4
16=4×3+4
那么,摆放n张餐桌应放的椅子数为:4n+4.
当n=10时,4×10+4
=40+4
=44(人)
答:10张桌子可以坐44人.
4.
第二十二关
1.
2.解:(1)结和图形我们可以得出:
图①有4个顶点、6条边、这些边围成3个区域;
图②有7个顶点、9条边、这些边围成3个区域;
图③有8个顶点、12条边、这些边围成5个区域;
图④有10个顶点、15条边、这些边围成6区域.
(2)根据以上数据,顶点用m表示,边数用n表
示,区域用f表示,他们的关系可表示为:m+f=n+1;
(3)把m=20,f=11代入上式得:n=m+f﹣1=20+11﹣1=30.
故如果平面图形有20个顶点和11个区域,那么这个平面图形的边数为30.
答案:m+f=n+1;30.
3.解:由图案和提供的数据可知:837,439第2位都是3,所以只有第2行和第4行是这两个数,第2行和第4行的末尾数字图形是7或者9,而571是其中一个数,第1行和第3行只有第一行的第2个图形是前面的那个7或9,所以第1行的数字是571,第2行是439,第3行是206,第4行是837;
即0,1,2,3,4,5,6,7,8,9分别用符号:
2018是:
第二十三关
1、12,6;36,42.
2×6=12(cm);6×6=36(cm);
2×3=6(cm?);(1+2+3+4+5+6)×2=42(cm?);
解:由图可知:
第1幅:?1个白色小正方形,
第2幅:?6个白色小正方形(1+5),
第3幅:?6个白色小正方形,
按如图规律:
第4幅:?15个白色小正方形(1+5+9),第5幅:15个白色小正方形,
第6幅:?1+5+9+13=28个白色小正方形.故答案为:?28.
3.解:第一个图形白色小正方形的个数为1个,灰色小正方形的个数为6+2=8(个)
第二个图形白色小正方形的个数为:2个,灰色小正方形的个数为:6+2+2=10(个)
……
第n个图形的白色小正方形的个数为n个,灰色小正方形的个数为(6+2n)个
所以第10个图形白色小正方形的个数为:10个
灰色小正方形的个数为:6+2×10=26(个)
答:第10个图形中有10个白色小正方形,26个灰色小正方形.
答案:10;26.
4.解:由图可知:
图形标号①的小棍根数为5;
图形标号②的小棍根数为9;
图形标号③的小棍根数为13;
…
由该搭建方式可得出规律:图形标号每增加1,小棍的个数增加4,
所以可以得出规律:搭第⑥个图形需要小棍根数为:6×4+1=25(根)
第二十四关
1..解:摆一个正方形要小棒4根;
摆两个正方形要小棒(4+3)根,即7根;
摆三个正方形要小棒(4+3×2)根,即10根,
…,
所以摆n个正方形要小棒:4+3×(n﹣1)=3n+1(根);
n=10,3×10+1=31(根);
答:摆10个正方形一共需要31根小棒.
2.解:37÷4=9…1
9个周期余1盏,则是红灯,
红灯数:2×9+1=19(盏)
黄灯数和蓝灯数都是1×9=9(盏)
3.解:根据题意,n个点的线段数是:1+2+3+4…+n﹣1条线段.
6个点可画:1+2+3+4+5=15(条)
8个点可画:1+2+3+4+5+6+7=28(条)
答:6个点,一共可以连15条线段;8个点,一共可以连28条线段.
4.分析;
根据图意,先计算出大正方形的边长;第几幅图就有几个小正方形,大正方形的边长就被平均分成了几份,每增加一个小正方形就增加3个顶点;据此完成表格,再根据表格进行解答即可.
解:96÷4=24(厘米)
24÷3=8(厘米)
4+3+3=10(个)
正方形的个数
1
2
3
……
正方形的边长/cm
24
12
8
……
顶点的个数
4
7
10
……
(1)24÷4=6(个)
答:如果围成的每个小正方形的边长正好是4厘米,共围了6个小正方形.
(2)4+3(n﹣1)=3n+1(个)
答:当这根绳子正好围成n个正方形时,顶点的个数是(3n+1)个.
答案:6;(3n+1).
第二十五关
1.解:画出三角形OAB绕点O逆时针旋转90°后的图形(图中红色部分):
2.解:画出三角形绕点O顺时针旋转90°的图形(图中红色部分:
3.
4.解:作图如下:
2r×r÷2×2
=2r×r
=2×2×2
=8(平方厘米).
答:正方形的面积是8平方厘米.
5.解:在正方形内画一个面积最大的圆,标出圆心O(下图):
3.14×2=6.28(厘米)
3.14×()2
=3.14×1
=3.14(平方厘米)
答:这个圆的周长是6.28厘米,面积是3.14平方厘米.
6.
7.解:设共需剪裁n次:
3n+1=151,
n=50;
剪成151个扇形需要剪50次;答案:B.
第二十一关:我会操作
第二十二关:我会操作
第二十三关:我会操作
第二十四关:我会操作
第二十五关:我会操作
同课章节目录
