6.3.3平面向量的应用举例-【新教材】人教A版(2019)高中数学必修第二册同步课堂训练(word含答案)
文档属性
| 名称 | 6.3.3平面向量的应用举例-【新教材】人教A版(2019)高中数学必修第二册同步课堂训练(word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 53.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 00:00:00 | ||
图片预览

文档简介
2020-2021学年高一数学第二学期人教版(2019)必修第二册同步课堂
第六章 平面向量及其应用
6.3.3平面向量的应用举例
-53340127000课堂小练
课堂小练
1.已知正三角形 ABC 的边长为 23 ,平面 ABC 内的动点 P,M 满足 |AP|=1 , PM=MC ,则 |BM|2 的最大值是(?? )
A.?434?????????????????????????????????B.?494?????????????????????????????????C.?37+634?????????????????????????????????D.?37+2334
2.已知△ABC是等腰三角形,AB=AC=5,BC=6,点P在线段AC上运动,则| PB + PC |的取值范围是(??? )
A.?[3,4]???????????????????????????????B.?[125,6]???????????????????????????????C.?[6,8]???????????????????????????????D.?[245,8]
3.已知 A(2,1),B(23,0),C,D 四点均在函数f(x)=log2 axx+b 的图象上,若四边形ABCD为平行四边形,则四边形ABCD的面积是(??? )
A.?265???????????????????????????????????????B.?263???????????????????????????????????????C.?525???????????????????????????????????????D.?523
4.已知 F1 ? F2 分别是椭圆 C:x2a2+y2b2=1(a>b>0) 的左?右焦点,过 F1 的直线 l 交椭圆于 D ? E 两点, |DF1|=5|F1E| , |DF2|=2 ,且 DF2⊥x 轴.若点 P 是圆 O:x2+y2=1 上的一个动点,则 |PF1|?|PF2| 的取值范围是(??? )
A.?[3?,?5]?????????????????????????????????B.?[2?,?5]?????????????????????????????????C.?[2?,?4]?????????????????????????????????D.?[3?,?4]
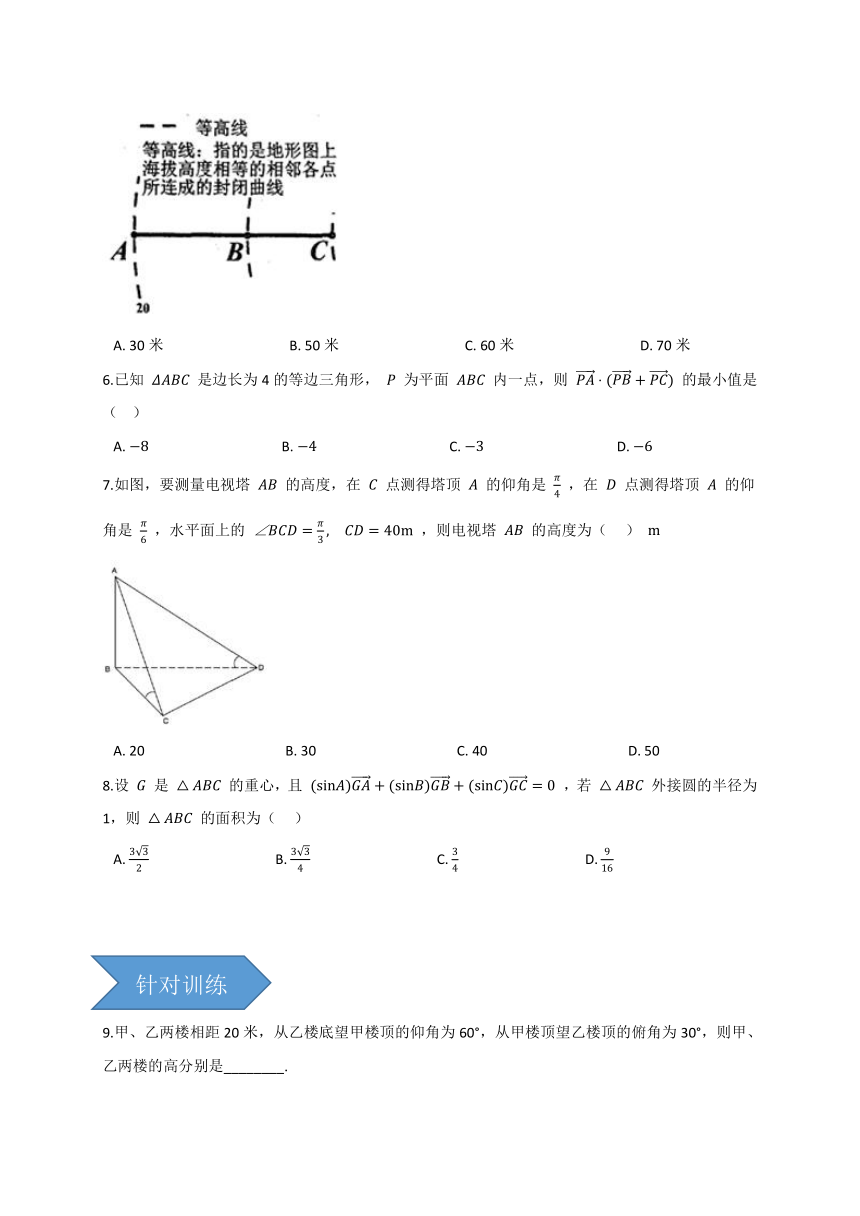
5.春秋以前中国已有“抱瓮而出灌”的原始提灌方式,使用提水吊杆——桔槔,后发展成辘轳.19世纪末,由于电动机的发明,离心泵得到了广泛应用,为发展机械提水灌溉提供了条件.图形如图所示为灌溉抽水管道在等高图的上垂直投影,在A处测得B处的仰角为37度,在A处测得C处的仰角为45度,在B处测得C处的仰角为53度,A点所在等高线值为20米,若BC管道长为50米,则B点所在等高线值为(??? )(参考数据 sin37°=35 )
A.?30米????????????????????????????????????B.?50米????????????????????????????????????C.?60米????????????????????????????????????D.?70米
6.已知 ΔABC 是边长为4的等边三角形, P 为平面 ABC 内一点,则 PA?(PB+PC) 的最小值是(?? )
A.??8??????????????????????????????????????B.??4??????????????????????????????????????C.??3??????????????????????????????????????D.??6
7.如图,要测量电视塔 AB 的高度,在 C 点测得塔顶 A 的仰角是 π4 ,在 D 点测得塔顶 A 的仰角是 π6 ,水平面上的 ∠BCD=π3,?CD=40m ,则电视塔 AB 的高度为(??? ) m
A.?20?????????????????????????????????????????B.?30?????????????????????????????????????????C.?40?????????????????????????????????????????D.?50
8.设 G 是 △ABC 的重心,且 (sinA)GA+(sinB)GB+(sinC)GC=0 ,若 △ABC 外接圆的半径为1,则 △ABC 的面积为(??? )
A.?332?????????????????????????????????????B.?334?????????????????????????????????????C.?34?????????????????????????????????????D.?916
-91440275590针对训练
针对训练
9.甲、乙两楼相距20米,从乙楼底望甲楼顶的仰角为60°,从甲楼顶望乙楼顶的俯角为30°,则甲、乙两楼的高分别是________.
10.已知 F1 , F2 是双曲线 Γ:x225?y29=1 的左、右焦点,点P为 Γ 上异于顶点的点,直线l分别与以 PF1 , PF2 为直径的圆相切于A,B两点,若向量 AB , F1F2 的夹角为 θ ,则 cosθ =________.
11.在 △ABC 中,角A,B,C所对的边分别为a,b,c,已知 cosBb+cosCc=1a ,且 a=4,b>a>c .
(1)求 bc 的值;
(2)若 △ABC 的面积 S=27 ,求 cosB .
12.已知 △ABC 的内角A,B,C的对边分别为a,b,c,且 asin(A+B?C)=csin(B+C) .
(1)求角C的大小
(2)若 2a+b=8 ,且 △ABC 的面积为 23 ,求 △ABC 的周长.
-10096594615答案解析
答案解析
1.【答案】 B
2.【答案】 D
3.【答案】 B
4.【答案】 A
5.【答案】 B
6.【答案】 D
7.【答案】 A
8.【答案】 B
9.【答案】 203 米、 4033 米
10.【答案】 33434
11.【答案】 (1)解:由已知和余弦定理得 a2+c2?b22acb+a2+b2?c22abc=1a ,
所以 a2+a2=2bc ,由 a=4 得 bc=16 ;
(2)解: S=12bcsinA=12×16sinA=27 ,
所以 sinA=74 ,因为 b>a>c ,所以 cosA=1?sin2A=34 ,
由余弦定理 cosA=b2+c2?a22cb=b2+c2?1632=34 ,
所以 b2+c2=40 ,又 bc=16 ,所以 b=42,c=22 ,
所以 cosB=a2+c2?b22ca=42+(22)2?(42)22×4×22=?24 .
12.【答案】 (1)解: ∵asin(A+B?C)=csin(B+C) ,
∴sinAsin(π?2C)=sinCsinA ,
∴2sinAsinCcosC=sinCsinA ,
∵sinAsinC≠0 ,
∴cosC=12,0∴C=π3 .
(2)解:由题意可得, 12ab32=23 ,
∴ab=8 ,
∵2a+b=8 联立可得, a=2,b=4 ,
由余弦定理可得, c2=12,c=23 ,
此时周长为 6+23 .
第六章 平面向量及其应用
6.3.3平面向量的应用举例
-53340127000课堂小练
课堂小练
1.已知正三角形 ABC 的边长为 23 ,平面 ABC 内的动点 P,M 满足 |AP|=1 , PM=MC ,则 |BM|2 的最大值是(?? )
A.?434?????????????????????????????????B.?494?????????????????????????????????C.?37+634?????????????????????????????????D.?37+2334
2.已知△ABC是等腰三角形,AB=AC=5,BC=6,点P在线段AC上运动,则| PB + PC |的取值范围是(??? )
A.?[3,4]???????????????????????????????B.?[125,6]???????????????????????????????C.?[6,8]???????????????????????????????D.?[245,8]
3.已知 A(2,1),B(23,0),C,D 四点均在函数f(x)=log2 axx+b 的图象上,若四边形ABCD为平行四边形,则四边形ABCD的面积是(??? )
A.?265???????????????????????????????????????B.?263???????????????????????????????????????C.?525???????????????????????????????????????D.?523
4.已知 F1 ? F2 分别是椭圆 C:x2a2+y2b2=1(a>b>0) 的左?右焦点,过 F1 的直线 l 交椭圆于 D ? E 两点, |DF1|=5|F1E| , |DF2|=2 ,且 DF2⊥x 轴.若点 P 是圆 O:x2+y2=1 上的一个动点,则 |PF1|?|PF2| 的取值范围是(??? )
A.?[3?,?5]?????????????????????????????????B.?[2?,?5]?????????????????????????????????C.?[2?,?4]?????????????????????????????????D.?[3?,?4]
5.春秋以前中国已有“抱瓮而出灌”的原始提灌方式,使用提水吊杆——桔槔,后发展成辘轳.19世纪末,由于电动机的发明,离心泵得到了广泛应用,为发展机械提水灌溉提供了条件.图形如图所示为灌溉抽水管道在等高图的上垂直投影,在A处测得B处的仰角为37度,在A处测得C处的仰角为45度,在B处测得C处的仰角为53度,A点所在等高线值为20米,若BC管道长为50米,则B点所在等高线值为(??? )(参考数据 sin37°=35 )
A.?30米????????????????????????????????????B.?50米????????????????????????????????????C.?60米????????????????????????????????????D.?70米
6.已知 ΔABC 是边长为4的等边三角形, P 为平面 ABC 内一点,则 PA?(PB+PC) 的最小值是(?? )
A.??8??????????????????????????????????????B.??4??????????????????????????????????????C.??3??????????????????????????????????????D.??6
7.如图,要测量电视塔 AB 的高度,在 C 点测得塔顶 A 的仰角是 π4 ,在 D 点测得塔顶 A 的仰角是 π6 ,水平面上的 ∠BCD=π3,?CD=40m ,则电视塔 AB 的高度为(??? ) m
A.?20?????????????????????????????????????????B.?30?????????????????????????????????????????C.?40?????????????????????????????????????????D.?50
8.设 G 是 △ABC 的重心,且 (sinA)GA+(sinB)GB+(sinC)GC=0 ,若 △ABC 外接圆的半径为1,则 △ABC 的面积为(??? )
A.?332?????????????????????????????????????B.?334?????????????????????????????????????C.?34?????????????????????????????????????D.?916
-91440275590针对训练
针对训练
9.甲、乙两楼相距20米,从乙楼底望甲楼顶的仰角为60°,从甲楼顶望乙楼顶的俯角为30°,则甲、乙两楼的高分别是________.
10.已知 F1 , F2 是双曲线 Γ:x225?y29=1 的左、右焦点,点P为 Γ 上异于顶点的点,直线l分别与以 PF1 , PF2 为直径的圆相切于A,B两点,若向量 AB , F1F2 的夹角为 θ ,则 cosθ =________.
11.在 △ABC 中,角A,B,C所对的边分别为a,b,c,已知 cosBb+cosCc=1a ,且 a=4,b>a>c .
(1)求 bc 的值;
(2)若 △ABC 的面积 S=27 ,求 cosB .
12.已知 △ABC 的内角A,B,C的对边分别为a,b,c,且 asin(A+B?C)=csin(B+C) .
(1)求角C的大小
(2)若 2a+b=8 ,且 △ABC 的面积为 23 ,求 △ABC 的周长.
-10096594615答案解析
答案解析
1.【答案】 B
2.【答案】 D
3.【答案】 B
4.【答案】 A
5.【答案】 B
6.【答案】 D
7.【答案】 A
8.【答案】 B
9.【答案】 203 米、 4033 米
10.【答案】 33434
11.【答案】 (1)解:由已知和余弦定理得 a2+c2?b22acb+a2+b2?c22abc=1a ,
所以 a2+a2=2bc ,由 a=4 得 bc=16 ;
(2)解: S=12bcsinA=12×16sinA=27 ,
所以 sinA=74 ,因为 b>a>c ,所以 cosA=1?sin2A=34 ,
由余弦定理 cosA=b2+c2?a22cb=b2+c2?1632=34 ,
所以 b2+c2=40 ,又 bc=16 ,所以 b=42,c=22 ,
所以 cosB=a2+c2?b22ca=42+(22)2?(42)22×4×22=?24 .
12.【答案】 (1)解: ∵asin(A+B?C)=csin(B+C) ,
∴sinAsin(π?2C)=sinCsinA ,
∴2sinAsinCcosC=sinCsinA ,
∵sinAsinC≠0 ,
∴cosC=12,0
(2)解:由题意可得, 12ab32=23 ,
∴ab=8 ,
∵2a+b=8 联立可得, a=2,b=4 ,
由余弦定理可得, c2=12,c=23 ,
此时周长为 6+23 .
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
