8.3.2 空间几何体的体积-【新教材】人教A版(2019)高中数学必修第二册同步课堂训练(word含答案)
文档属性
| 名称 | 8.3.2 空间几何体的体积-【新教材】人教A版(2019)高中数学必修第二册同步课堂训练(word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 202.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 08:21:05 | ||
图片预览

文档简介
2020-2021学年高一数学第二学期人教版(2019)必修第二册同步课堂
第八章 立体几何初步
8.3.2 空间几何体的体积
-53340127000课堂小练
课堂小练
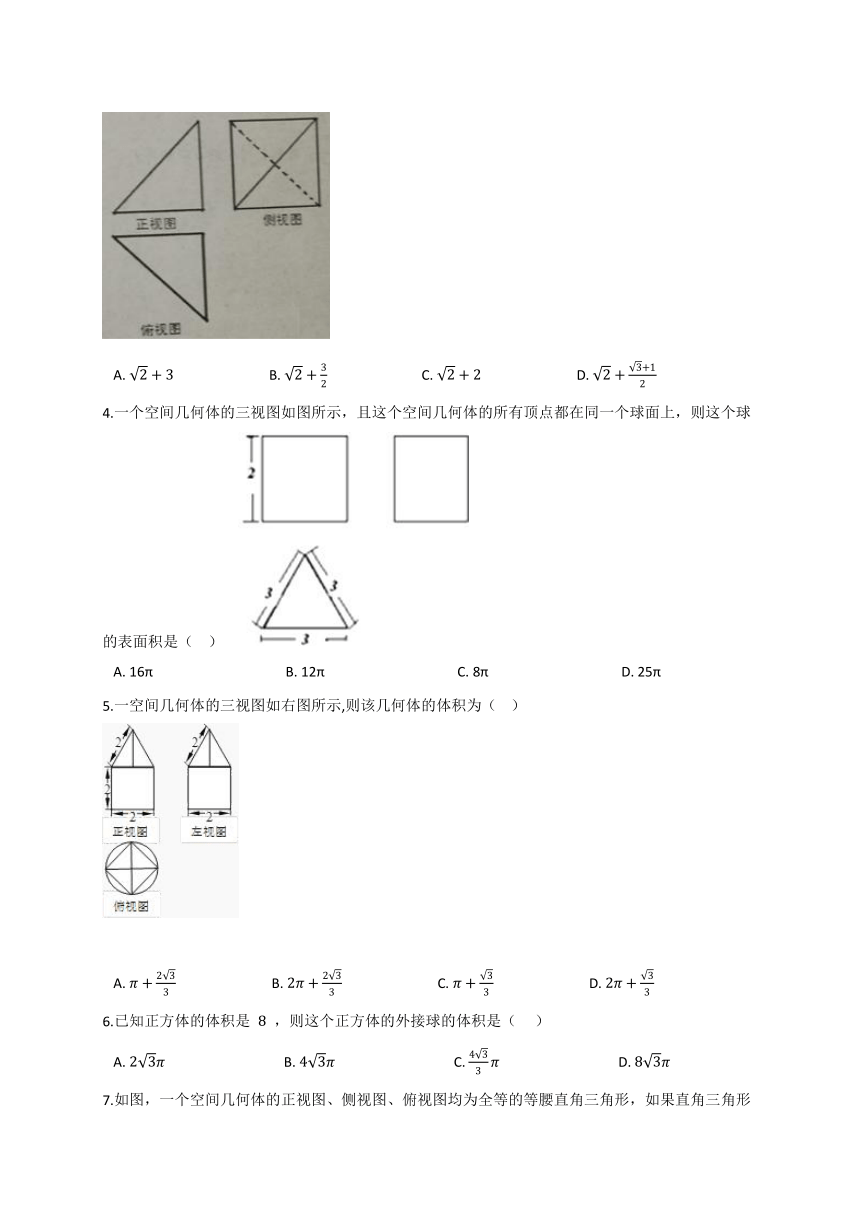
1.某空间几何体的三视图如图所示,则该几何体的体积为(??? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?4???????????????????????????????????????????D.?8
2.一空间几何体的三视图如下图所示,则该几何体的体积为(?? )?
A.?1???????????????????????????????????????????B.?3???????????????????????????????????????????C.?6???????????????????????????????????????????D.?2
3.一空间几何体的三视图如图所示,其中正视图和信视图均为边长为1的等腰直角三角形,则此空间几何体的表面积是( ??)
A.?2+3???????????????????????????B.?2+32???????????????????????????C.?2+2???????????????????????????D.?2+3+12
4.一个空间几何体的三视图如图所示,且这个空间几何体的所有顶点都在同一个球面上,则这个球的表面积是(?? )
A.?16π??????????????????????????????????????B.?12π??????????????????????????????????????C.?8π??????????????????????????????????????D.?25π
5.一空间几何体的三视图如右图所示,则该几何体的体积为(????)
?
A.?π+233????????????????????????????B.?2π+233????????????????????????????C.?π+33????????????????????????????D.?2π+33
6.已知正方体的体积是 8 ,则这个正方体的外接球的体积是(??? )
A.?23π??????????????????????????????????B.?43π??????????????????????????????????C.?433π??????????????????????????????????D.?83π
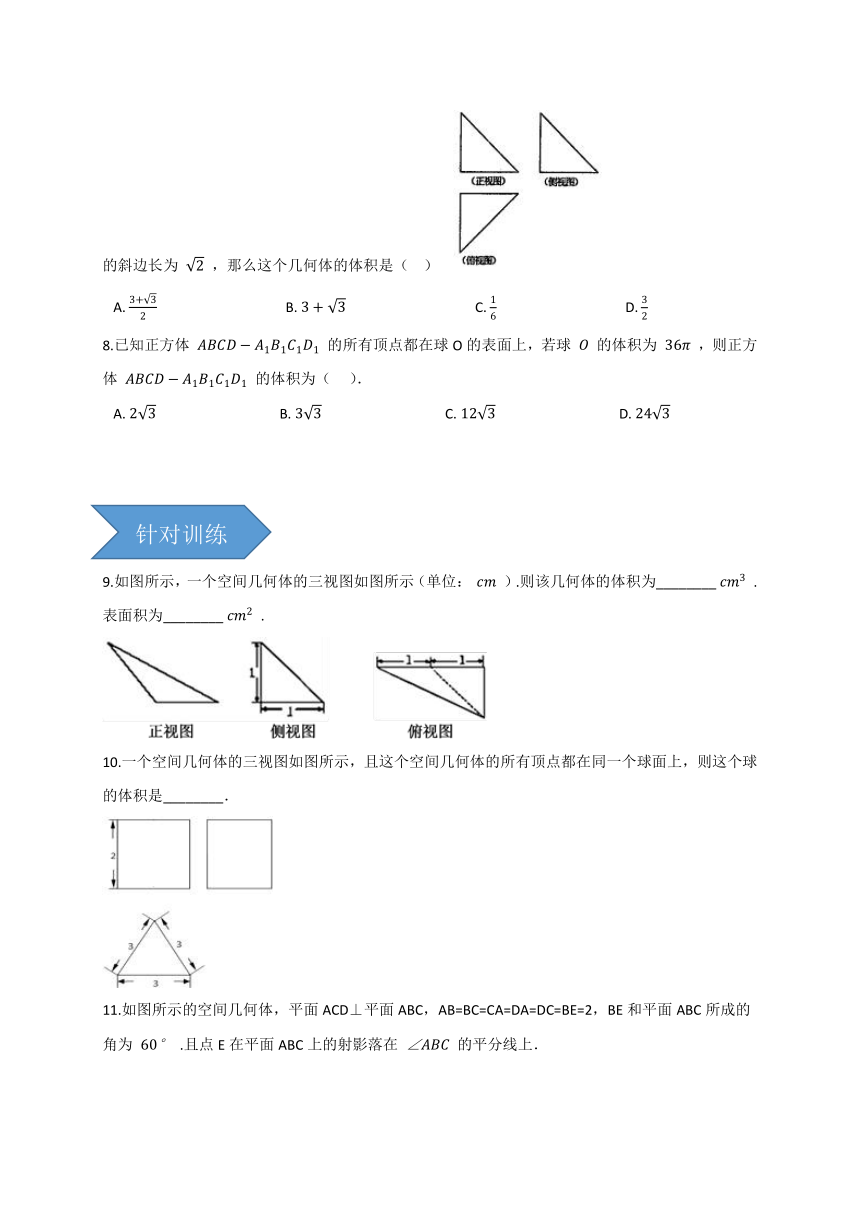
7.如图,一个空间几何体的正视图、侧视图、俯视图均为全等的等腰直角三角形,如果直角三角形的斜边长为 2 ,那么这个几何体的体积是(?? )
A.?3+32?????????????????????????????????????B.?3+3?????????????????????????????????????C.?16?????????????????????????????????????D.?32
8.已知正方体 ABCD?A1B1C1D1 的所有顶点都在球O的表面上,若球 O 的体积为 36π ,则正方体 ABCD?A1B1C1D1 的体积为(??? ).
A.?23????????????????????????????????????B.?33????????????????????????????????????C.?123????????????????????????????????????D.?243
-91440275590针对训练
针对训练
9.如图所示,一个空间几何体的三视图如图所示(单位: cm ).则该几何体的体积为________ cm3 .表面积为________ cm2 .
10.一个空间几何体的三视图如图所示,且这个空间几何体的所有顶点都在同一个球面上,则这个球的体积是________.
11.如图所示的空间几何体,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为 60° .且点E在平面ABC上的射影落在 ∠ABC 的平分线上.
(1)求证:DE//平面ABC;
(2)求二面角E—BC—A的余弦;
(3)求多面体ABCDE的体积.
12.如图是一个空间几何体的三视图,其正视图与侧视图是边长为4cm的正三角形、俯视图中正方形的边长为4cm,
(1)画出这个几何体的直观图(不用写作图步骤);
(2)请写出这个几何体的名称,并指出它的高是多少;
(3)求出这个几何体的表面积。
-10096594615答案解析
答案解析
1.【答案】 C
2.【答案】 D
3.【答案】 D
4.【答案】A
5.【答案】 B
6.【答案】 B
7.【答案】C
8.【答案】 D
9.【答案】 16;2+3+52
10.【答案】323π
11.【答案】 (1)解:由题意知,△ABC,△ACD都是边长为2的等边三角形,
取AC中点O,连接BO,DO,
则BO⊥AC,DO⊥AC∵平面ACD⊥平面ABC
∴DO⊥平面ABC,作EF⊥平面ABC,
那么EF∥DO,根据题意,点F落在BO上,
∴∠EBF=60?,易求得EF=DO= 3
所以四边形DEFO是平行四边形,DE∥OF;∵DE?平面ABC,OF?平面ABC,∴DE∥平面ABC
(2)解:作FG⊥BC,垂足为G,连接EG;
∵EF⊥平面ABC,根据三垂线定理可知,EG⊥BC,
∴∠EGF就是二面角E?BC?A的平面角,
∴EG=EF2?FG2=132∴cos∠EGF=FGEG=1313 ,
即二面角E?BC?A的余弦值为 1313 .
(3)解:∵平面ACD⊥平面ABC,OB⊥AC∴OB⊥平面ACD;
又∵DE∥OB∴DE⊥平面DAC,
∴三棱锥E?DAC的体积 V1=13S△BAC?DE=13?3?(3-1)=3-33
又三棱锥E?ABC的体积 V2=13S△ABC?EF=13?3?3=1 ,
∴多面体DE?ABC的体积为 V=V1+V2=6?33
12.【答案】 (1)解:如图:
(2)解:正四棱锥
高为 23
(3)解:表面积为48cm2
第八章 立体几何初步
8.3.2 空间几何体的体积
-53340127000课堂小练
课堂小练
1.某空间几何体的三视图如图所示,则该几何体的体积为(??? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?4???????????????????????????????????????????D.?8
2.一空间几何体的三视图如下图所示,则该几何体的体积为(?? )?
A.?1???????????????????????????????????????????B.?3???????????????????????????????????????????C.?6???????????????????????????????????????????D.?2
3.一空间几何体的三视图如图所示,其中正视图和信视图均为边长为1的等腰直角三角形,则此空间几何体的表面积是( ??)
A.?2+3???????????????????????????B.?2+32???????????????????????????C.?2+2???????????????????????????D.?2+3+12
4.一个空间几何体的三视图如图所示,且这个空间几何体的所有顶点都在同一个球面上,则这个球的表面积是(?? )
A.?16π??????????????????????????????????????B.?12π??????????????????????????????????????C.?8π??????????????????????????????????????D.?25π
5.一空间几何体的三视图如右图所示,则该几何体的体积为(????)
?
A.?π+233????????????????????????????B.?2π+233????????????????????????????C.?π+33????????????????????????????D.?2π+33
6.已知正方体的体积是 8 ,则这个正方体的外接球的体积是(??? )
A.?23π??????????????????????????????????B.?43π??????????????????????????????????C.?433π??????????????????????????????????D.?83π
7.如图,一个空间几何体的正视图、侧视图、俯视图均为全等的等腰直角三角形,如果直角三角形的斜边长为 2 ,那么这个几何体的体积是(?? )
A.?3+32?????????????????????????????????????B.?3+3?????????????????????????????????????C.?16?????????????????????????????????????D.?32
8.已知正方体 ABCD?A1B1C1D1 的所有顶点都在球O的表面上,若球 O 的体积为 36π ,则正方体 ABCD?A1B1C1D1 的体积为(??? ).
A.?23????????????????????????????????????B.?33????????????????????????????????????C.?123????????????????????????????????????D.?243
-91440275590针对训练
针对训练
9.如图所示,一个空间几何体的三视图如图所示(单位: cm ).则该几何体的体积为________ cm3 .表面积为________ cm2 .
10.一个空间几何体的三视图如图所示,且这个空间几何体的所有顶点都在同一个球面上,则这个球的体积是________.
11.如图所示的空间几何体,平面ACD⊥平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为 60° .且点E在平面ABC上的射影落在 ∠ABC 的平分线上.
(1)求证:DE//平面ABC;
(2)求二面角E—BC—A的余弦;
(3)求多面体ABCDE的体积.
12.如图是一个空间几何体的三视图,其正视图与侧视图是边长为4cm的正三角形、俯视图中正方形的边长为4cm,
(1)画出这个几何体的直观图(不用写作图步骤);
(2)请写出这个几何体的名称,并指出它的高是多少;
(3)求出这个几何体的表面积。
-10096594615答案解析
答案解析
1.【答案】 C
2.【答案】 D
3.【答案】 D
4.【答案】A
5.【答案】 B
6.【答案】 B
7.【答案】C
8.【答案】 D
9.【答案】 16;2+3+52
10.【答案】323π
11.【答案】 (1)解:由题意知,△ABC,△ACD都是边长为2的等边三角形,
取AC中点O,连接BO,DO,
则BO⊥AC,DO⊥AC∵平面ACD⊥平面ABC
∴DO⊥平面ABC,作EF⊥平面ABC,
那么EF∥DO,根据题意,点F落在BO上,
∴∠EBF=60?,易求得EF=DO= 3
所以四边形DEFO是平行四边形,DE∥OF;∵DE?平面ABC,OF?平面ABC,∴DE∥平面ABC
(2)解:作FG⊥BC,垂足为G,连接EG;
∵EF⊥平面ABC,根据三垂线定理可知,EG⊥BC,
∴∠EGF就是二面角E?BC?A的平面角,
∴EG=EF2?FG2=132∴cos∠EGF=FGEG=1313 ,
即二面角E?BC?A的余弦值为 1313 .
(3)解:∵平面ACD⊥平面ABC,OB⊥AC∴OB⊥平面ACD;
又∵DE∥OB∴DE⊥平面DAC,
∴三棱锥E?DAC的体积 V1=13S△BAC?DE=13?3?(3-1)=3-33
又三棱锥E?ABC的体积 V2=13S△ABC?EF=13?3?3=1 ,
∴多面体DE?ABC的体积为 V=V1+V2=6?33
12.【答案】 (1)解:如图:
(2)解:正四棱锥
高为 23
(3)解:表面积为48cm2
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
