9.1随机抽样-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册专题训练(word含答案)
文档属性
| 名称 | 9.1随机抽样-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册专题训练(word含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 182.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 00:00:00 | ||
图片预览


文档简介
1236980011785600高一数学人教版(2019)必修第二册
【9.1随机抽样专题训练】
【基础巩固】
1.某商铺统计了今年5个月的用电量y(单位:10kw/h)与月份x的对应数据,列表如下:
x
2
4
5
6
8
y
30
40
57
a
69
根据表中数据求出 y 关于 x 的线性回归方程为 y=6.5x+17.5 ,则上表中 a 的值为(??? )
A.?50????????????????????????????????????????B.?54????????????????????????????????????????C.?56.5????????????????????????????????????????D.?64
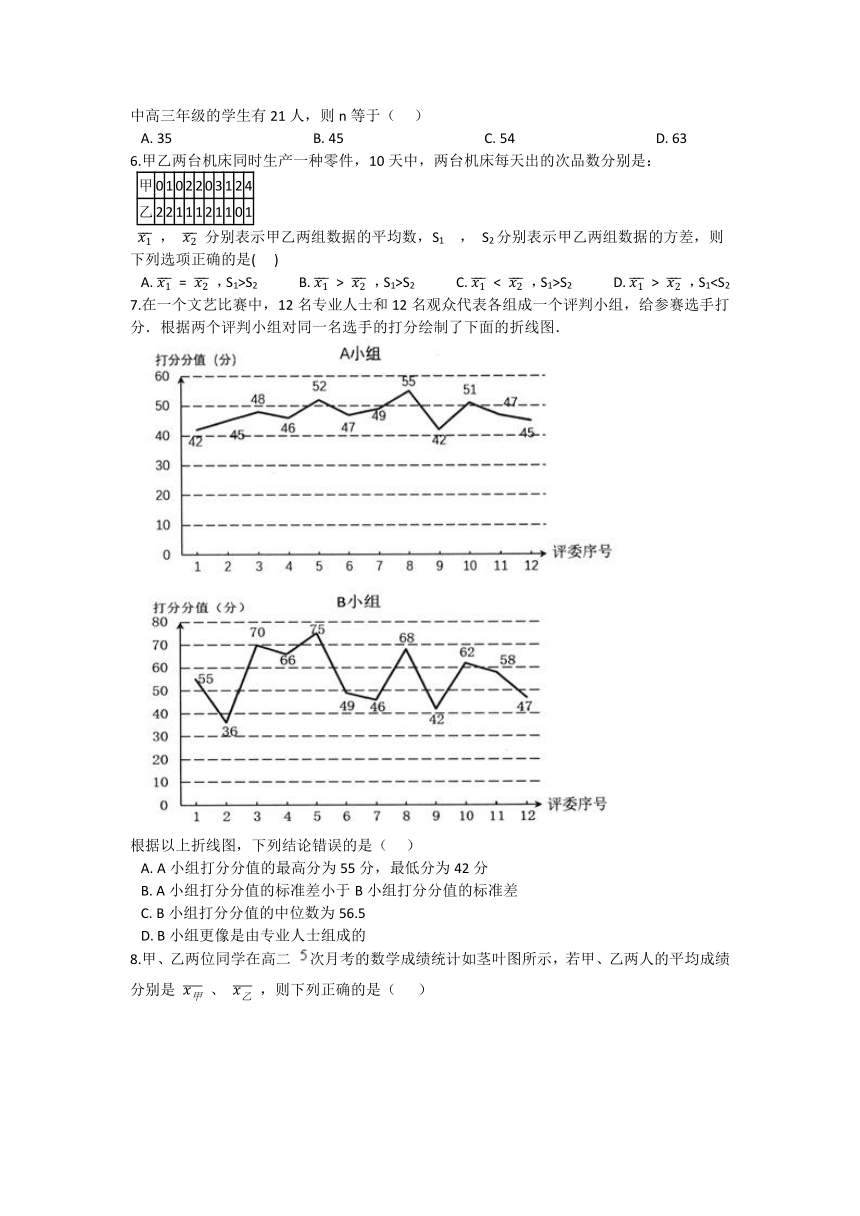
2.某工厂对一批新产品的长度(单位:mm)进行检测,检测结果的频率分布直方图如图所示,据此估计这批产品的中位数为(??? )
A.?20??????????????????????????????????????B.?25??????????????????????????????????????C.?22.5??????????????????????????????????????D.?22.75
3.晓霞在学校的“经典诗词朗诵”大赛中,5位评委给她的分数分别是:93,93,95,96,92,则晓霞得分的中位数与平均数分别是(??? )
A.?93;93???????????????????????????B.?93;93.8???????????????????????????C.?93.5;93.5???????????????????????????D.?94;93.8
4.某地气象局把当地某月(共30天)每一天的最低气温作了统计,并绘制了如下图所示的统计图.记这组数据的众数为M,中位数为N,平均数为P,则(??? )
A.?M5.某中学高一、高二、高三年级的学生人数之比依次为6:5:7,防疫站欲对该校学生进行身体健康调查,用分层抽样的方法从该校高中三个年级的学生中抽取容量为n的样本,样本中高三年级的学生有21人,则n等于(??? )
A.?35?????????????????????????????????????????B.?45?????????????????????????????????????????C.?54?????????????????????????????????????????D.?63
6.甲乙两台机床同时生产一种零件,10天中,两台机床每天出的次品数分别是:
甲
0
1
0
2
2
0
3
1
2
4
乙
2
2
1
1
1
2
1
1
0
1
x1 , x2 分别表示甲乙两组数据的平均数,S1 , S2分别表示甲乙两组数据的方差,则下列选项正确的是( ???)
A.?x1 = x2 ,S1>S2????????????B.?x1 > x2 ,S1>S2????????????C.?x1 < x2 ,S1>S2????????????D.?x1 > x2 ,S17.在一个文艺比赛中,12名专业人士和12名观众代表各组成一个评判小组,给参赛选手打分.根据两个评判小组对同一名选手的打分绘制了下面的折线图.
根据以上折线图,下列结论错误的是(??? )
A.?A小组打分分值的最高分为55分,最低分为42分
B.?A小组打分分值的标准差小于B小组打分分值的标准差
C.?B小组打分分值的中位数为56.5
D.?B小组更像是由专业人士组成的
8.甲、乙两位同学在高二 次月考的数学成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别是 x甲 、 x乙 ,则下列正确的是(???? )
A.?x甲x乙 ,乙比甲成绩稳定
C.?x甲>x乙 ,甲比乙成绩稳定?????????????????????????????????D.?x甲9.已知数据 a1,a2,...,an 的平均数为 a ,方差为 S2 ,则数据 2a1,2a2,...,2an 的平均数和方差为 (??? )
A.?a,S2?????????????????????????????????B.?2a,S2?????????????????????????????????C.?2a,4S2?????????????????????????????????D.?2a,2S2
10.惠州市某工厂 10 名工人某天生产同一类型零件,生产的件数分别是10、12、14 、14、15 、15 、16 、17 、17 、17,记这组数据的平均数为a,中位数为b,众数为c,则(??? )
A.?a>b>c???????????????????????????????B.?b>c>a???????????????????????????????C.?c>a>b???????????????????????????????D.?c>b>a
【培优提升】
11.某高中各年级男、女生人数统计如表:
年级
人数
性别
高一
高二
高三
男生
592
563
520
女生
528
517
a
按年级分层抽样,若抽取该校学生80人中,高二学生有27人,则表中a=________.
12.假设要考察某公司生产的500克袋装牛奶的三聚青氨是否超标,现从800袋牛奶中抽取60袋进行检验,利用随机数表抽取样本时,先将800袋牛奶按000,001,…,799进行编号,如果从随机数表第7行第8列的数开始向右读,请你依次写出最先检测的3袋牛奶的编号________.
(下面摘取了随机数表第7行至第9行)
84 42 17 53 31? 57 24 55 06 88? 77 04 74 47 67? 21 76 33 50 25? 83 92 12 06 76
63 01 63 78 59? 16 95 56 67 19? 98 10 50 71 75? 12 86 73 58 07? 44 39 52 38 79
33 21 12 34 29? 78 64 56 07 82? 52 42 0744 38? 15 51 00 13 42? 99 66 02 79 54.
13.若某中学7个班参加“庆国庆”歌咏比赛的得分如茎叶图所示,则这组数据的中位数是________.
14.某工厂生产 A 、 B 两种型号的不同产品,产品数量之比为 2:3 .用分层抽样的方法抽出一个样本容量为 n 的样本,则其中 A 种型号的产品有 14 件.现从样本中抽出两件产品,此时含有 A 型号产品的概率为________.
15.某中学举行了一次“交通安全知识竞赛”, 全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
组别
分组
频数
频率
第1组
[50,60)
8
0.16
第2组
[60,70)
a
▓
第3组
[70,80)
20
0.40
第4组
[80,90)
▓
0.08
第5组
[90,100]
2
b
合计
▓
▓
(1)写出 a,b,x,y 的值;
(2)若现在需要采用分层抽样的方式从5个小组中抽取25人去参加市里的抽测考试,则第1,2,3组应分别抽取多少人?
(3)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加交通安全知识的志愿宣传活动.求所抽取的2名同学中至少有1名同学来自第5组的概率.
16.某校为了了解高三学生某次月考数学成绩的情况,抽取这次月考100名学生的数学成绩(分数都在 [50,150] 内),按数学成绩分皮 [50,70) , [70,90) , [90,110) , [110,130) , [130,150] 这5组,得到频率分布直方图如图所示.
(1)估计这次月考该校高三学生数学成绩的中位数(结果保留一位小数);
(2)若从数学成绩在 [110,150] 内的学生中采用分层抽样的方法随机抽取5人,再从这5人中随机抽取2人,求至少有1人的数学成绩在 [130,150] 内的概率.
17.某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),现用分层抽样方法(按A类,B类分二层)从该工厂的工人中共抽取100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
(1)A类工人和B类工人各抽取多少人?
(2)将A类工人和B类工人的抽查结果分别绘制成频率分布直方图(如图1和图2).
①就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
②分别估计A类工人和B类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组中的数据用该组区间的中点值作代表).
18.某次数学测试后,数学老师对该班n位同学的成绩进行分析,全班同学的成绩都分布在区间 [95?,?145] ,制成的频率分布直方图如图所示.已知成绩在区间 [125?,?135) 的有12人.
(1)求n;
(2)根据频率分布直方图,估计本次测试该班的数学平均分(同一组数据用该组数据区间的中点值表示).
(3)现从 [125?,?135) , [135?,?145] 两个分数段的试卷中,按分层抽样的方法共抽取了6份试卷.若从这6份试卷中随机选出2份作为优秀试卷,求选出2份优秀试卷中恰有1份分数在 [135?,?145] 的概率.
【参考答案】
1.【答案】 B
2.【答案】 C
3.【答案】 B
4.【答案】 A
5.【答案】 C
6.【答案】 B
7.【答案】 D
8.【答案】 D
9.【答案】 C
10.【答案】 D
二、培优提升
11.【答案】 480
12.【答案】 331、572、455
13.【答案】 91
14.【答案】 1117
15.【答案】 (1)解:根据分组在[50,60)的频数是8,频率是0.16,故可得样本容量为 80.16=50 ;
故可得频数分布表为:
组别
分组
频数
频率
第1组
[50,60)
8
0.16
第2组
[60,70)
a =16
0.32
第3组
[70,80)
20
0.40
第4组
[80,90)
4
0.08
第5组
[90,100]
2
b =0.04
合计
50
1
则 a=16,b=0.04 ;
由此可得: x=0.3210=0.032 ; y=0.0410=0.004
(2)解:从50人中抽取25人,故抽样比为 12 ,
故从第一组抽取 8×12=4 人;从第二组抽取 16×12=8 人;从第三组抽取 20×12=10 人
(3)解:第四组[80,90)中共有4人;第五组[90,100]共有2人,
从以上所有人中抽取2人,共有 C62=15 种可能;
则抽取的2人全部来自第四组共有 C42=6 种可能,
故抽取的2人至少有1人来自第五组共有 15?6=9 种可能,
故满足题意的概率 P=915=35
16.【答案】 (1)解:因为 (0.004+0.010)×20=0.28<0.5 , (0.004+0.010+0.021)×20=0.7>0.5 ,
所以中位数在 [90,110) 内.
设中位数为 m .则 m?90110?90×0.021×20=0.5?0.28 ,
解得 m≈100.5 ,即这次月考该校高三学生数学成绩的中位数约为100.5分
(2)解:由题意可得这次月考数学成绩在 [110,130) 的人数为 100×0.009×20=18 ,
这次月考数学成绩在 [130,150] 的人数为 100×0.006×20=12 ,
则采用分层抽样的方法随机抽取的5人中,数学成绩在[110,130)的学生有3人,记为 a , b , c ,数学成绩在 [130,150] 的学生有2人,记为 D , E .
从这5人中随机抽取 2 人的情况有 ab , ac , aD , aE , bc , bD , bE , cD , cE , DE ,共10种,
其中符合条件的情况有 aD , aE , bD , bE , cD , cE , DE ,共7种,
故所求概率 P=710
17.【答案】 (1)解:A类工人中应抽取: 250×110=25 人,B类工人中应抽取: 750×110=75 人.
(2)解:①从直方图可以判断:B类工人中个体间的差异程度更小.
② xA=0.16×105+0.32×115+0.20×125+0.20×135+0.12×145=123 ,
xB=0.08×115+0.20×125+0.48×135+0.24×145=133.8 ,
x=25100×123+75100×133.8=131.1 ,
A类工人生产能力的平均数,B类工人生产能力的平均数以及全工厂工人生产能力的平均数的估计值分别为123,133.8和131.1
18.【答案】 (1)解:由题可知: n=120.02×10=60
(2)解: x=100×0.15+110×0.25+120×0.3+130×0.2+140×0.1=118.5
(3)解:由频率分布直方图可知:成绩分布在 [125,135) 有12人,在 [135,145) 有6人,抽取比例为 618=13 ,所以 [125,135) 内抽取人数为4人, [135,145) 抽取人数为2人.
记 [125,135) 中4人为a,b,c,d,记 [135,145) 的2人分别为e,f,
则所有的抽取结果为:(a,b),(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f)共15种.
恰有一份分数段在 [135,145) 有(a,e),(a,f),(b,e),(b,f),(c,e),(c,f),(d,e),(d,f)共8种,
所以,概率 P=815
【9.1随机抽样专题训练】
【基础巩固】
1.某商铺统计了今年5个月的用电量y(单位:10kw/h)与月份x的对应数据,列表如下:
x
2
4
5
6
8
y
30
40
57
a
69
根据表中数据求出 y 关于 x 的线性回归方程为 y=6.5x+17.5 ,则上表中 a 的值为(??? )
A.?50????????????????????????????????????????B.?54????????????????????????????????????????C.?56.5????????????????????????????????????????D.?64
2.某工厂对一批新产品的长度(单位:mm)进行检测,检测结果的频率分布直方图如图所示,据此估计这批产品的中位数为(??? )
A.?20??????????????????????????????????????B.?25??????????????????????????????????????C.?22.5??????????????????????????????????????D.?22.75
3.晓霞在学校的“经典诗词朗诵”大赛中,5位评委给她的分数分别是:93,93,95,96,92,则晓霞得分的中位数与平均数分别是(??? )
A.?93;93???????????????????????????B.?93;93.8???????????????????????????C.?93.5;93.5???????????????????????????D.?94;93.8
4.某地气象局把当地某月(共30天)每一天的最低气温作了统计,并绘制了如下图所示的统计图.记这组数据的众数为M,中位数为N,平均数为P,则(??? )
A.?M
A.?35?????????????????????????????????????????B.?45?????????????????????????????????????????C.?54?????????????????????????????????????????D.?63
6.甲乙两台机床同时生产一种零件,10天中,两台机床每天出的次品数分别是:
甲
0
1
0
2
2
0
3
1
2
4
乙
2
2
1
1
1
2
1
1
0
1
x1 , x2 分别表示甲乙两组数据的平均数,S1 , S2分别表示甲乙两组数据的方差,则下列选项正确的是( ???)
A.?x1 = x2 ,S1>S2????????????B.?x1 > x2 ,S1>S2????????????C.?x1 < x2 ,S1>S2????????????D.?x1 > x2 ,S1
根据以上折线图,下列结论错误的是(??? )
A.?A小组打分分值的最高分为55分,最低分为42分
B.?A小组打分分值的标准差小于B小组打分分值的标准差
C.?B小组打分分值的中位数为56.5
D.?B小组更像是由专业人士组成的
8.甲、乙两位同学在高二 次月考的数学成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别是 x甲 、 x乙 ,则下列正确的是(???? )
A.?x甲
C.?x甲>x乙 ,甲比乙成绩稳定?????????????????????????????????D.?x甲
A.?a,S2?????????????????????????????????B.?2a,S2?????????????????????????????????C.?2a,4S2?????????????????????????????????D.?2a,2S2
10.惠州市某工厂 10 名工人某天生产同一类型零件,生产的件数分别是10、12、14 、14、15 、15 、16 、17 、17 、17,记这组数据的平均数为a,中位数为b,众数为c,则(??? )
A.?a>b>c???????????????????????????????B.?b>c>a???????????????????????????????C.?c>a>b???????????????????????????????D.?c>b>a
【培优提升】
11.某高中各年级男、女生人数统计如表:
年级
人数
性别
高一
高二
高三
男生
592
563
520
女生
528
517
a
按年级分层抽样,若抽取该校学生80人中,高二学生有27人,则表中a=________.
12.假设要考察某公司生产的500克袋装牛奶的三聚青氨是否超标,现从800袋牛奶中抽取60袋进行检验,利用随机数表抽取样本时,先将800袋牛奶按000,001,…,799进行编号,如果从随机数表第7行第8列的数开始向右读,请你依次写出最先检测的3袋牛奶的编号________.
(下面摘取了随机数表第7行至第9行)
84 42 17 53 31? 57 24 55 06 88? 77 04 74 47 67? 21 76 33 50 25? 83 92 12 06 76
63 01 63 78 59? 16 95 56 67 19? 98 10 50 71 75? 12 86 73 58 07? 44 39 52 38 79
33 21 12 34 29? 78 64 56 07 82? 52 42 0744 38? 15 51 00 13 42? 99 66 02 79 54.
13.若某中学7个班参加“庆国庆”歌咏比赛的得分如茎叶图所示,则这组数据的中位数是________.
14.某工厂生产 A 、 B 两种型号的不同产品,产品数量之比为 2:3 .用分层抽样的方法抽出一个样本容量为 n 的样本,则其中 A 种型号的产品有 14 件.现从样本中抽出两件产品,此时含有 A 型号产品的概率为________.
15.某中学举行了一次“交通安全知识竞赛”, 全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
组别
分组
频数
频率
第1组
[50,60)
8
0.16
第2组
[60,70)
a
▓
第3组
[70,80)
20
0.40
第4组
[80,90)
▓
0.08
第5组
[90,100]
2
b
合计
▓
▓
(1)写出 a,b,x,y 的值;
(2)若现在需要采用分层抽样的方式从5个小组中抽取25人去参加市里的抽测考试,则第1,2,3组应分别抽取多少人?
(3)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加交通安全知识的志愿宣传活动.求所抽取的2名同学中至少有1名同学来自第5组的概率.
16.某校为了了解高三学生某次月考数学成绩的情况,抽取这次月考100名学生的数学成绩(分数都在 [50,150] 内),按数学成绩分皮 [50,70) , [70,90) , [90,110) , [110,130) , [130,150] 这5组,得到频率分布直方图如图所示.
(1)估计这次月考该校高三学生数学成绩的中位数(结果保留一位小数);
(2)若从数学成绩在 [110,150] 内的学生中采用分层抽样的方法随机抽取5人,再从这5人中随机抽取2人,求至少有1人的数学成绩在 [130,150] 内的概率.
17.某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),现用分层抽样方法(按A类,B类分二层)从该工厂的工人中共抽取100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
(1)A类工人和B类工人各抽取多少人?
(2)将A类工人和B类工人的抽查结果分别绘制成频率分布直方图(如图1和图2).
①就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
②分别估计A类工人和B类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组中的数据用该组区间的中点值作代表).
18.某次数学测试后,数学老师对该班n位同学的成绩进行分析,全班同学的成绩都分布在区间 [95?,?145] ,制成的频率分布直方图如图所示.已知成绩在区间 [125?,?135) 的有12人.
(1)求n;
(2)根据频率分布直方图,估计本次测试该班的数学平均分(同一组数据用该组数据区间的中点值表示).
(3)现从 [125?,?135) , [135?,?145] 两个分数段的试卷中,按分层抽样的方法共抽取了6份试卷.若从这6份试卷中随机选出2份作为优秀试卷,求选出2份优秀试卷中恰有1份分数在 [135?,?145] 的概率.
【参考答案】
1.【答案】 B
2.【答案】 C
3.【答案】 B
4.【答案】 A
5.【答案】 C
6.【答案】 B
7.【答案】 D
8.【答案】 D
9.【答案】 C
10.【答案】 D
二、培优提升
11.【答案】 480
12.【答案】 331、572、455
13.【答案】 91
14.【答案】 1117
15.【答案】 (1)解:根据分组在[50,60)的频数是8,频率是0.16,故可得样本容量为 80.16=50 ;
故可得频数分布表为:
组别
分组
频数
频率
第1组
[50,60)
8
0.16
第2组
[60,70)
a =16
0.32
第3组
[70,80)
20
0.40
第4组
[80,90)
4
0.08
第5组
[90,100]
2
b =0.04
合计
50
1
则 a=16,b=0.04 ;
由此可得: x=0.3210=0.032 ; y=0.0410=0.004
(2)解:从50人中抽取25人,故抽样比为 12 ,
故从第一组抽取 8×12=4 人;从第二组抽取 16×12=8 人;从第三组抽取 20×12=10 人
(3)解:第四组[80,90)中共有4人;第五组[90,100]共有2人,
从以上所有人中抽取2人,共有 C62=15 种可能;
则抽取的2人全部来自第四组共有 C42=6 种可能,
故抽取的2人至少有1人来自第五组共有 15?6=9 种可能,
故满足题意的概率 P=915=35
16.【答案】 (1)解:因为 (0.004+0.010)×20=0.28<0.5 , (0.004+0.010+0.021)×20=0.7>0.5 ,
所以中位数在 [90,110) 内.
设中位数为 m .则 m?90110?90×0.021×20=0.5?0.28 ,
解得 m≈100.5 ,即这次月考该校高三学生数学成绩的中位数约为100.5分
(2)解:由题意可得这次月考数学成绩在 [110,130) 的人数为 100×0.009×20=18 ,
这次月考数学成绩在 [130,150] 的人数为 100×0.006×20=12 ,
则采用分层抽样的方法随机抽取的5人中,数学成绩在[110,130)的学生有3人,记为 a , b , c ,数学成绩在 [130,150] 的学生有2人,记为 D , E .
从这5人中随机抽取 2 人的情况有 ab , ac , aD , aE , bc , bD , bE , cD , cE , DE ,共10种,
其中符合条件的情况有 aD , aE , bD , bE , cD , cE , DE ,共7种,
故所求概率 P=710
17.【答案】 (1)解:A类工人中应抽取: 250×110=25 人,B类工人中应抽取: 750×110=75 人.
(2)解:①从直方图可以判断:B类工人中个体间的差异程度更小.
② xA=0.16×105+0.32×115+0.20×125+0.20×135+0.12×145=123 ,
xB=0.08×115+0.20×125+0.48×135+0.24×145=133.8 ,
x=25100×123+75100×133.8=131.1 ,
A类工人生产能力的平均数,B类工人生产能力的平均数以及全工厂工人生产能力的平均数的估计值分别为123,133.8和131.1
18.【答案】 (1)解:由题可知: n=120.02×10=60
(2)解: x=100×0.15+110×0.25+120×0.3+130×0.2+140×0.1=118.5
(3)解:由频率分布直方图可知:成绩分布在 [125,135) 有12人,在 [135,145) 有6人,抽取比例为 618=13 ,所以 [125,135) 内抽取人数为4人, [135,145) 抽取人数为2人.
记 [125,135) 中4人为a,b,c,d,记 [135,145) 的2人分别为e,f,
则所有的抽取结果为:(a,b),(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f)共15种.
恰有一份分数段在 [135,145) 有(a,e),(a,f),(b,e),(b,f),(c,e),(c,f),(d,e),(d,f)共8种,
所以,概率 P=815
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
