10.3频率与概率-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册专题训练(word含答案)
文档属性
| 名称 | 10.3频率与概率-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册专题训练(word含答案) | 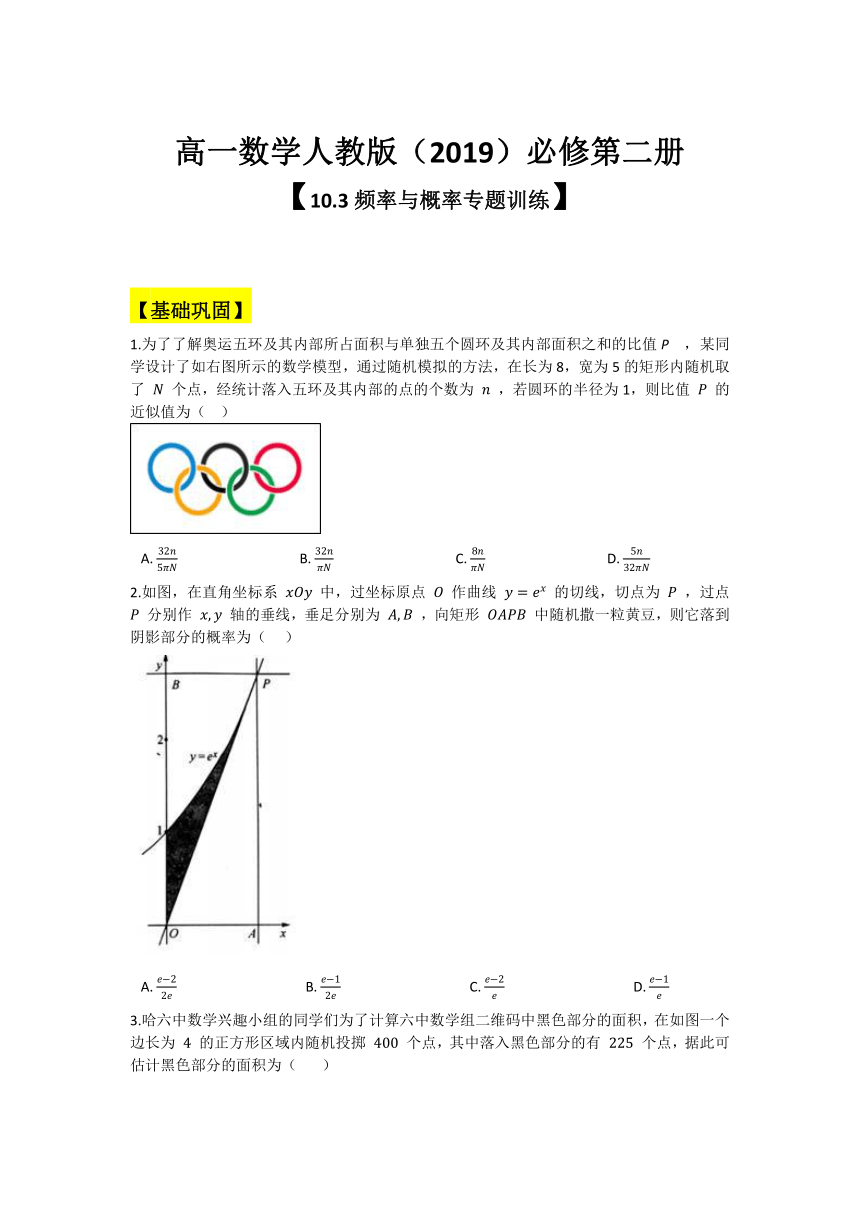 | |
| 格式 | docx | ||
| 文件大小 | 154.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 08:27:08 | ||
图片预览




文档简介
1201420011595100高一数学人教版(2019)必修第二册
【10.3频率与概率专题训练】
【基础巩固】
1.为了了解奥运五环及其内部所占面积与单独五个圆环及其内部面积之和的比值P , 某同学设计了如右图所示的数学模型,通过随机模拟的方法,在长为8,宽为5的矩形内随机取了 N 个点,经统计落入五环及其内部的点的个数为 n ,若圆环的半径为1,则比值 P 的近似值为(?? )
A.?32n5πN???????????????????????????????????B.?32nπN???????????????????????????????????C.?8nπN???????????????????????????????????D.?5n32πN
2.如图,在直角坐标系 xOy 中,过坐标原点 O 作曲线 y=ex 的切线,切点为 P ,过点 P 分别作 x,y 轴的垂线,垂足分别为 A,B ,向矩形 OAPB 中随机撒一粒黄豆,则它落到阴影部分的概率为(??? )
A.?e?22e?????????????????????????????????????B.?e?12e?????????????????????????????????????C.?e?2e?????????????????????????????????????D.?e?1e
3.哈六中数学兴趣小组的同学们为了计算六中数学组二维码中黑色部分的面积,在如图一个边长为 4 的正方形区域内随机投掷 400 个点,其中落入黑色部分的有 225 个点,据此可估计黑色部分的面积为(????? )
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
4.分别以正方形ABCD的四条边为直径画半圆,重叠部分如图中阴影区域所示,若向该正方形内随机投一点,则该点落在阴影区域的概率为(?? )
A.?4?π2????????????????????????????????????B.?π?22????????????????????????????????????C.?4?π4????????????????????????????????????D.?π?24
5.如图所示,分别以正方形ABCD两邻边AB、AD为直径向正方形内做两个半圆,交于点O.若向正方形内投掷一颗质地均匀的小球(小球落到每点的可能性均相同),则该球落在阴影部分的概率为( ??)
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
6.“纹样”是中国艺术宝库的瑰宝,“火纹”是常见的一种传统纹样.为了测算某火纹纹样(如图阴影部分所示)的面积,作一个边长为5的正方形将其包含在内,并向该正方形内随机投掷1000个点,己知恰有400个点落在阴影部分,据此可估计阴影部分的面积是(?? )
A.?2??????????????????????????????????????????B.?3??????????????????????????????????????????C.?10??????????????????????????????????????????D.?15
7.下列关于用转盘进行随机模拟的说法中正确的是( ??)
A.?旋转的次数的多少不会影响估计的结果???????????????B.?旋转的次数越多,估计的结果越精确
C.?旋转时可以按规律旋转???????????????????????????????????????D.?转盘的半径越大,估计的结果越精确
8.关于圆周率 π ,数学发展史上出现过许多有创意的求法,如著名的普丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计 π 的值:先请120名同学每人随机写下一个 x,y 都小于1的正实数对 (x,y) ,再统计其中 x,y 能与1构成钝角三角形三边的数对 (x,y) 的个数m,最后根据统计个数m估计 π 的值.如果统计结果是 m=34 ,那么可以估计 π 的值为(??? )
A.?227???????????????????????????????????????B.?4715???????????????????????????????????????C.?5116???????????????????????????????????????D.?5317
9.在如图所示的正方形中随机投掷10000个点,若曲线 C 的方程为 x2+y?1=0(x>0,y>0) ,则落入阴影部分的点的个数的估计为(??? )
A.?5000??????????????????????????????????B.?6667??????????????????????????????????C.?7500??????????????????????????????????D.?7854
10.通过模拟试验,产生了20组随机数
7130? 3013? 7055? 7430? 7740
4122? 7884? 2604? 3346? 0952
6107? 9706? 5774? 5725? 6576
5929? 1768? 6071? 9138? 6254
每组随机数中,如果恰有三个数在1,2,3,4,5,6中,则表示恰有三次击中目标,问四次射击中恰有三次击中目标的概率约为(? )
A.?320????????????????????????????????????????B.?15????????????????????????????????????????C.?14????????????????????????????????????????D.?920
【培优提升】
11.如图,一不规则区域内,有一边长为1米的正方形,向区域内随机地撒1 000颗黄豆,数得落在正方形区域内(含边界)的黄豆数为400颗,以此实验数据为依据可以估计出该不规则图形的面积为________平方米.(用分数作答)
12.我国古代数学家刘徽创立的“割圆术”可以估算圆周率π,理论上能把π的值计算到任意精度,祖冲之继承并发展了“割圆术”,将π的值精确到小数点后七位,其结果领先世界一千多年,“割圆术”的第一步是计算单位圆内接正六边形的面积S6 , S6=________.
13.如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分,在正方形ABCD中任取一点P,则点P恰好取自阴影部分的概率为________.
14.如图,在边长为1的正方形中随机撒1000粒豆子,有380粒落到阴影部分,据此估计阴影部分的面积为________.
15.设AB=6,在线段AB上任取两点C、D(端点A、B除外),将线段AB分成三条线段AC、CD、DB.
(1)若分成的三条线段的长度均为正整数,求这三条线段可以构成三角形(称为事件A)的概率;
(2)若分成的三条线段的长度均为正实数,求这三条线段可以构成三角形(称为事件B)的概率;
(3)根据以下用计算机所产生的20组随机数,试用随机数模拟的方法,来近似计算(2)中事件B的概率,
20组随机数如下:
组别
1
2
3
4
5
6
7
8
9
10
?X
?0.52
?0.36
?0.58
?0.73
?0.41
?0.6
?0.05
?0.32
0.38
?0.73
?Y
?0.76
0.39
0.37
0.01
0.04
0.28
0.03
?0.15
0.14
0.86
组别
?11
?12
13
14
15
16
17
18
19
20
?X
?0.67
?0.47
0.58
?0.21
0.54
?0.64
0.36
?0.35
0.95
?0.14
?Y
?0.41
0.54
?0.51
0.37
?0.31
0.23
?0.56
0.89
?0.17
0.03
(X和Y都是0~1之间的均匀随机数)
16.如图,面积为 S 的正方形 ABCD 中有一个不规则的图形 M ,可按下面方法估计 M 的面积:在正方形 ABCD 中随机投掷 n 个点,若 n 个点中有 m 个点落入 M 中,则 M 的面积的估计值为 mnS ,假设正方形 ABCD 的边长为2, M 的面积为1,并向正方形 ABCD 中随机投掷 10000 个点,以 X 表示落入 M 中的点的数目.
(I)求 X 的均值 EX ;
(II)求用以上方法估计 M 的面积时, M 的面积的估计值与实际值之差在区间 (?0.03,0.03) 内的概率.
附表: P(k)=t=0kC10000t×0.25t×0.7510000?t
17.解答题
(1)在边长为1的正方形ABCD内任取一点M,求事件“|AM|≤1”的概率;
(2)某班在一次数学活动中,老师让全班56名同学每人随机写下一对都小于1的正实数x、y,统计出两数能与1构成锐角三角形的三边长的数对(x,y)共有12对,请据此估计π的近似值(精确到0.001).
18.设O为坐标原点,点P的坐标(x﹣2,x﹣y)
(1)在一个盒子中,放有标号为1,2,3的三张卡片,现从此盒中有放回地先后抽到两张卡片的标号分别记为x,y,求|OP|的最大值,并求事件“|OP|取到最大值”的概率;
(2)若利用计算机随机在[0,3]上先后取两个数分别记为x,y,求P点在第一象限的概率.
【参考答案】
1.【答案】 C
2.【答案】 A
3.【答案】 C
4.【答案】 B
5.【答案】 C
6.【答案】 C
7.【答案】 B
8.【答案】 B
9.【答案】 B
10.【答案】 B
11.【答案】 52
12.【答案】 332
13.【答案】23
14.【答案】0.38
15.【答案】 (1)解:若分成的三条线段的长度均为正整数,则三条线段的长度的所有可能为:
1,1,4;1,2,3;1,3,2;1,4,1;
2,1,3;2,2,2;2,3,1;
3,1,2;3,2,1;
4,1,1,
共10种情况,其中只有三条线段为2,2,2时能构成三角形
则构成三角形的概率p= 110
(2)解:由题意知本题是一个几何概型
设其中两条线段长度分别为x,y,
则第三条线段长度为6﹣x﹣y,
则全部结果所构成的区域为:
0<x<6,0<y<6,0<6﹣x﹣y<6,
即为0<x<6,0<y<6,0<x+y<6
所表示的平面区域为三角形OAB;
若三条线段x,y,6﹣x﹣y,能构成三角形,
则还要满足 {x+y>6?x?yx+6?x?y>yy+6?x?y>x ,即为 {x+y>3y<3x<3 ,
所表示的平面区域为三角形DEF,
由几何概型知所求的概率为:P= S△DEFS△AOB = 14
(3)解:步骤如下:
①产生两组0~1之间的均匀随机数X、Y(题目给出)
②经平移和伸缩变换,a=6X,b=6Y,
③数出落在0<x<6,0<y<6,0<6﹣x﹣y<6的点(a,b)的个数N和落在0<x<3,0<y<3,0<6﹣x﹣y<6,6﹣x﹣y+y>x,x+y>6﹣x﹣y
的点(a,b)的个数N1 , 由已知中的20组随机数可数得N=13,N1=3
④由 SBSΩ=N1N = 313 ,故P(B)= 313 .
16.【答案】 解:(I) EX=10000×14=2500 (II)依题意所求概率为 P(?0.0317.【答案】 (1)解:如图,在边长为1的正方形ABCD内任取一点M,满足条件的点M落在扇形BAD内(图中阴影部分),由几何概型概率计算公式,有: P ( | M A | ≤ 1 ) = S阴影部分/S正方形ABCD =π4 ,
故事件“|AM|≤1”发生的概率为 π4 .
(2)以点A为坐标原点,AB为x轴,AD为y轴建立平面直角坐标系,如图所示:
任取两个小于1的正数x,y,所有基本事件构成区域 Ω = { ( x , y ) | { 0 < x < 1 ;0 < y < 1 } ,
, 即正方形ABCD内部;
事件N=“以x,y与1为边长能构成锐角三角形”包含的基本事件构成区域
, 即扇形BAD以外正方形ABCD以内的阴影部分;
由(1)知:P(N)=1?π4
全班56名同学每人随机写下一对都小于1的正实数x、y,可以看作在区域Ω中任取56个点;满足“以x,y与1为边长能构成锐角三角形”的(x,y)共有12对,即有12个点落在区域N中,
故其概率为1256=314 , 用频率估计概率,有1?π4≈314,即π4≈11 ,
∴π≈1114×4=227≈3.143即π的近似值为3.143.
18.【答案】 (1)解:记抽到的卡片标号为(x,y),所有的情况分别为,
(x,y)
(1,1)
(1,2)
(1,3)
(2,1)
(2,2)
(2,3)
(3,1)
(3,2)
(3,3)
P(x﹣2,x﹣y)
(﹣1,0)
(﹣1,﹣1)
(﹣1,﹣2)
(0,1)
(0,0)
(0,﹣1)
(1,2)
(1,1)
(1,0)
|OP|
1
2
5
1
0
1
5
2
1
共9种.由表格可知|OP|的最大值为 5
设事件A为“|OP|取到最大值”,则满足事件A的(x,y)有(1,3),(3,1)两种情况,
∴ P(A)=29
(2)解:设事件B为“P点在第一象限”
若 {0≤x≤30≤y≤3 ,其所表示的区域面积为3×3=9,
由题意可得事件B满足 {0≤x≤30≤y≤3x?2>0x?y>0 ,
即如图所示的阴影部分,
其区域面积为 1×3?12×1×1=52
∴ P(B)=529=518
【10.3频率与概率专题训练】
【基础巩固】
1.为了了解奥运五环及其内部所占面积与单独五个圆环及其内部面积之和的比值P , 某同学设计了如右图所示的数学模型,通过随机模拟的方法,在长为8,宽为5的矩形内随机取了 N 个点,经统计落入五环及其内部的点的个数为 n ,若圆环的半径为1,则比值 P 的近似值为(?? )
A.?32n5πN???????????????????????????????????B.?32nπN???????????????????????????????????C.?8nπN???????????????????????????????????D.?5n32πN
2.如图,在直角坐标系 xOy 中,过坐标原点 O 作曲线 y=ex 的切线,切点为 P ,过点 P 分别作 x,y 轴的垂线,垂足分别为 A,B ,向矩形 OAPB 中随机撒一粒黄豆,则它落到阴影部分的概率为(??? )
A.?e?22e?????????????????????????????????????B.?e?12e?????????????????????????????????????C.?e?2e?????????????????????????????????????D.?e?1e
3.哈六中数学兴趣小组的同学们为了计算六中数学组二维码中黑色部分的面积,在如图一个边长为 4 的正方形区域内随机投掷 400 个点,其中落入黑色部分的有 225 个点,据此可估计黑色部分的面积为(????? )
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
4.分别以正方形ABCD的四条边为直径画半圆,重叠部分如图中阴影区域所示,若向该正方形内随机投一点,则该点落在阴影区域的概率为(?? )
A.?4?π2????????????????????????????????????B.?π?22????????????????????????????????????C.?4?π4????????????????????????????????????D.?π?24
5.如图所示,分别以正方形ABCD两邻边AB、AD为直径向正方形内做两个半圆,交于点O.若向正方形内投掷一颗质地均匀的小球(小球落到每点的可能性均相同),则该球落在阴影部分的概率为( ??)
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
6.“纹样”是中国艺术宝库的瑰宝,“火纹”是常见的一种传统纹样.为了测算某火纹纹样(如图阴影部分所示)的面积,作一个边长为5的正方形将其包含在内,并向该正方形内随机投掷1000个点,己知恰有400个点落在阴影部分,据此可估计阴影部分的面积是(?? )
A.?2??????????????????????????????????????????B.?3??????????????????????????????????????????C.?10??????????????????????????????????????????D.?15
7.下列关于用转盘进行随机模拟的说法中正确的是( ??)
A.?旋转的次数的多少不会影响估计的结果???????????????B.?旋转的次数越多,估计的结果越精确
C.?旋转时可以按规律旋转???????????????????????????????????????D.?转盘的半径越大,估计的结果越精确
8.关于圆周率 π ,数学发展史上出现过许多有创意的求法,如著名的普丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计 π 的值:先请120名同学每人随机写下一个 x,y 都小于1的正实数对 (x,y) ,再统计其中 x,y 能与1构成钝角三角形三边的数对 (x,y) 的个数m,最后根据统计个数m估计 π 的值.如果统计结果是 m=34 ,那么可以估计 π 的值为(??? )
A.?227???????????????????????????????????????B.?4715???????????????????????????????????????C.?5116???????????????????????????????????????D.?5317
9.在如图所示的正方形中随机投掷10000个点,若曲线 C 的方程为 x2+y?1=0(x>0,y>0) ,则落入阴影部分的点的个数的估计为(??? )
A.?5000??????????????????????????????????B.?6667??????????????????????????????????C.?7500??????????????????????????????????D.?7854
10.通过模拟试验,产生了20组随机数
7130? 3013? 7055? 7430? 7740
4122? 7884? 2604? 3346? 0952
6107? 9706? 5774? 5725? 6576
5929? 1768? 6071? 9138? 6254
每组随机数中,如果恰有三个数在1,2,3,4,5,6中,则表示恰有三次击中目标,问四次射击中恰有三次击中目标的概率约为(? )
A.?320????????????????????????????????????????B.?15????????????????????????????????????????C.?14????????????????????????????????????????D.?920
【培优提升】
11.如图,一不规则区域内,有一边长为1米的正方形,向区域内随机地撒1 000颗黄豆,数得落在正方形区域内(含边界)的黄豆数为400颗,以此实验数据为依据可以估计出该不规则图形的面积为________平方米.(用分数作答)
12.我国古代数学家刘徽创立的“割圆术”可以估算圆周率π,理论上能把π的值计算到任意精度,祖冲之继承并发展了“割圆术”,将π的值精确到小数点后七位,其结果领先世界一千多年,“割圆术”的第一步是计算单位圆内接正六边形的面积S6 , S6=________.
13.如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分,在正方形ABCD中任取一点P,则点P恰好取自阴影部分的概率为________.
14.如图,在边长为1的正方形中随机撒1000粒豆子,有380粒落到阴影部分,据此估计阴影部分的面积为________.
15.设AB=6,在线段AB上任取两点C、D(端点A、B除外),将线段AB分成三条线段AC、CD、DB.
(1)若分成的三条线段的长度均为正整数,求这三条线段可以构成三角形(称为事件A)的概率;
(2)若分成的三条线段的长度均为正实数,求这三条线段可以构成三角形(称为事件B)的概率;
(3)根据以下用计算机所产生的20组随机数,试用随机数模拟的方法,来近似计算(2)中事件B的概率,
20组随机数如下:
组别
1
2
3
4
5
6
7
8
9
10
?X
?0.52
?0.36
?0.58
?0.73
?0.41
?0.6
?0.05
?0.32
0.38
?0.73
?Y
?0.76
0.39
0.37
0.01
0.04
0.28
0.03
?0.15
0.14
0.86
组别
?11
?12
13
14
15
16
17
18
19
20
?X
?0.67
?0.47
0.58
?0.21
0.54
?0.64
0.36
?0.35
0.95
?0.14
?Y
?0.41
0.54
?0.51
0.37
?0.31
0.23
?0.56
0.89
?0.17
0.03
(X和Y都是0~1之间的均匀随机数)
16.如图,面积为 S 的正方形 ABCD 中有一个不规则的图形 M ,可按下面方法估计 M 的面积:在正方形 ABCD 中随机投掷 n 个点,若 n 个点中有 m 个点落入 M 中,则 M 的面积的估计值为 mnS ,假设正方形 ABCD 的边长为2, M 的面积为1,并向正方形 ABCD 中随机投掷 10000 个点,以 X 表示落入 M 中的点的数目.
(I)求 X 的均值 EX ;
(II)求用以上方法估计 M 的面积时, M 的面积的估计值与实际值之差在区间 (?0.03,0.03) 内的概率.
附表: P(k)=t=0kC10000t×0.25t×0.7510000?t
17.解答题
(1)在边长为1的正方形ABCD内任取一点M,求事件“|AM|≤1”的概率;
(2)某班在一次数学活动中,老师让全班56名同学每人随机写下一对都小于1的正实数x、y,统计出两数能与1构成锐角三角形的三边长的数对(x,y)共有12对,请据此估计π的近似值(精确到0.001).
18.设O为坐标原点,点P的坐标(x﹣2,x﹣y)
(1)在一个盒子中,放有标号为1,2,3的三张卡片,现从此盒中有放回地先后抽到两张卡片的标号分别记为x,y,求|OP|的最大值,并求事件“|OP|取到最大值”的概率;
(2)若利用计算机随机在[0,3]上先后取两个数分别记为x,y,求P点在第一象限的概率.
【参考答案】
1.【答案】 C
2.【答案】 A
3.【答案】 C
4.【答案】 B
5.【答案】 C
6.【答案】 C
7.【答案】 B
8.【答案】 B
9.【答案】 B
10.【答案】 B
11.【答案】 52
12.【答案】 332
13.【答案】23
14.【答案】0.38
15.【答案】 (1)解:若分成的三条线段的长度均为正整数,则三条线段的长度的所有可能为:
1,1,4;1,2,3;1,3,2;1,4,1;
2,1,3;2,2,2;2,3,1;
3,1,2;3,2,1;
4,1,1,
共10种情况,其中只有三条线段为2,2,2时能构成三角形
则构成三角形的概率p= 110
(2)解:由题意知本题是一个几何概型
设其中两条线段长度分别为x,y,
则第三条线段长度为6﹣x﹣y,
则全部结果所构成的区域为:
0<x<6,0<y<6,0<6﹣x﹣y<6,
即为0<x<6,0<y<6,0<x+y<6
所表示的平面区域为三角形OAB;
若三条线段x,y,6﹣x﹣y,能构成三角形,
则还要满足 {x+y>6?x?yx+6?x?y>yy+6?x?y>x ,即为 {x+y>3y<3x<3 ,
所表示的平面区域为三角形DEF,
由几何概型知所求的概率为:P= S△DEFS△AOB = 14
(3)解:步骤如下:
①产生两组0~1之间的均匀随机数X、Y(题目给出)
②经平移和伸缩变换,a=6X,b=6Y,
③数出落在0<x<6,0<y<6,0<6﹣x﹣y<6的点(a,b)的个数N和落在0<x<3,0<y<3,0<6﹣x﹣y<6,6﹣x﹣y+y>x,x+y>6﹣x﹣y
的点(a,b)的个数N1 , 由已知中的20组随机数可数得N=13,N1=3
④由 SBSΩ=N1N = 313 ,故P(B)= 313 .
16.【答案】 解:(I) EX=10000×14=2500 (II)依题意所求概率为 P(?0.03
故事件“|AM|≤1”发生的概率为 π4 .
(2)以点A为坐标原点,AB为x轴,AD为y轴建立平面直角坐标系,如图所示:
任取两个小于1的正数x,y,所有基本事件构成区域 Ω = { ( x , y ) | { 0 < x < 1 ;0 < y < 1 } ,
, 即正方形ABCD内部;
事件N=“以x,y与1为边长能构成锐角三角形”包含的基本事件构成区域
, 即扇形BAD以外正方形ABCD以内的阴影部分;
由(1)知:P(N)=1?π4
全班56名同学每人随机写下一对都小于1的正实数x、y,可以看作在区域Ω中任取56个点;满足“以x,y与1为边长能构成锐角三角形”的(x,y)共有12对,即有12个点落在区域N中,
故其概率为1256=314 , 用频率估计概率,有1?π4≈314,即π4≈11 ,
∴π≈1114×4=227≈3.143即π的近似值为3.143.
18.【答案】 (1)解:记抽到的卡片标号为(x,y),所有的情况分别为,
(x,y)
(1,1)
(1,2)
(1,3)
(2,1)
(2,2)
(2,3)
(3,1)
(3,2)
(3,3)
P(x﹣2,x﹣y)
(﹣1,0)
(﹣1,﹣1)
(﹣1,﹣2)
(0,1)
(0,0)
(0,﹣1)
(1,2)
(1,1)
(1,0)
|OP|
1
2
5
1
0
1
5
2
1
共9种.由表格可知|OP|的最大值为 5
设事件A为“|OP|取到最大值”,则满足事件A的(x,y)有(1,3),(3,1)两种情况,
∴ P(A)=29
(2)解:设事件B为“P点在第一象限”
若 {0≤x≤30≤y≤3 ,其所表示的区域面积为3×3=9,
由题意可得事件B满足 {0≤x≤30≤y≤3x?2>0x?y>0 ,
即如图所示的阴影部分,
其区域面积为 1×3?12×1×1=52
∴ P(B)=529=518
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
