3.3 圆周角和圆心角的关系(1)
图片预览


文档简介
(共25张PPT)
3.3 圆周角和圆心角的关系(1)
大兴学校 卿丽萍
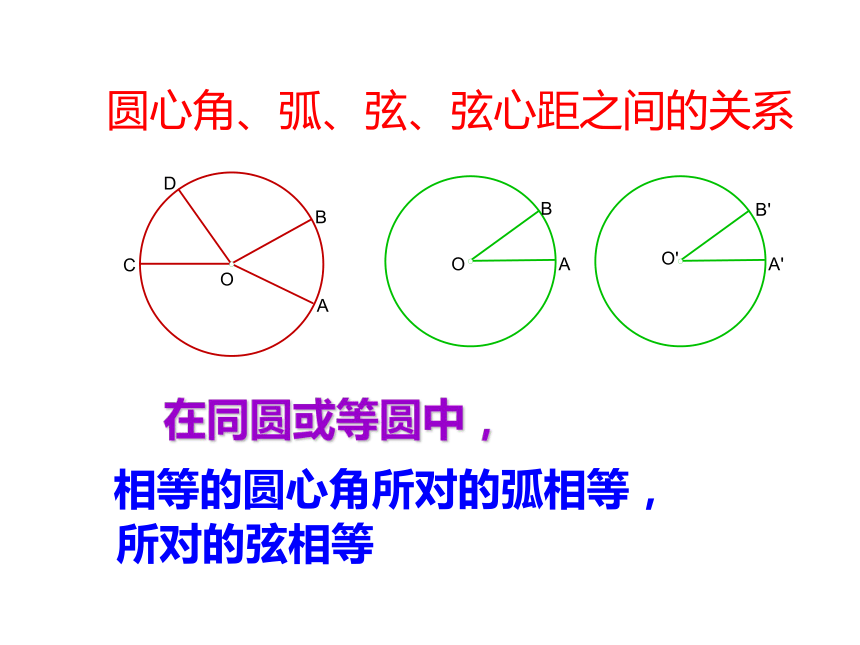
圆心角、弧、弦、弦心距之间的关系
在同圆或等圆中,
相等的圆心角所对的弧相等,
所对的弦相等
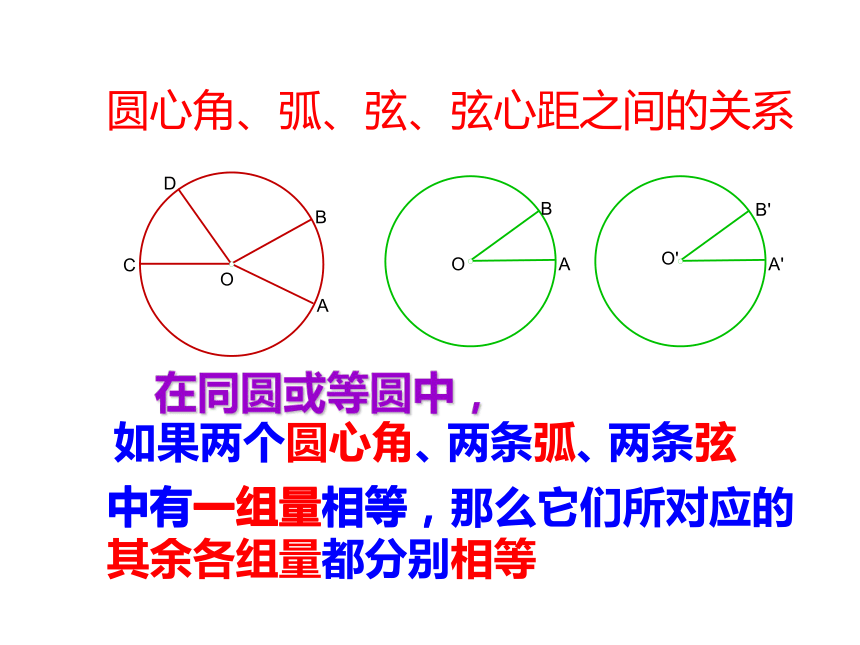
圆心角、弧、弦、弦心距之间的关系
在同圆或等圆中,
如果两个圆心角、
两条弧、
两条弦
中有一组量相等,
中有一组量相等,那么它们所对应的其余各组量都分别相等
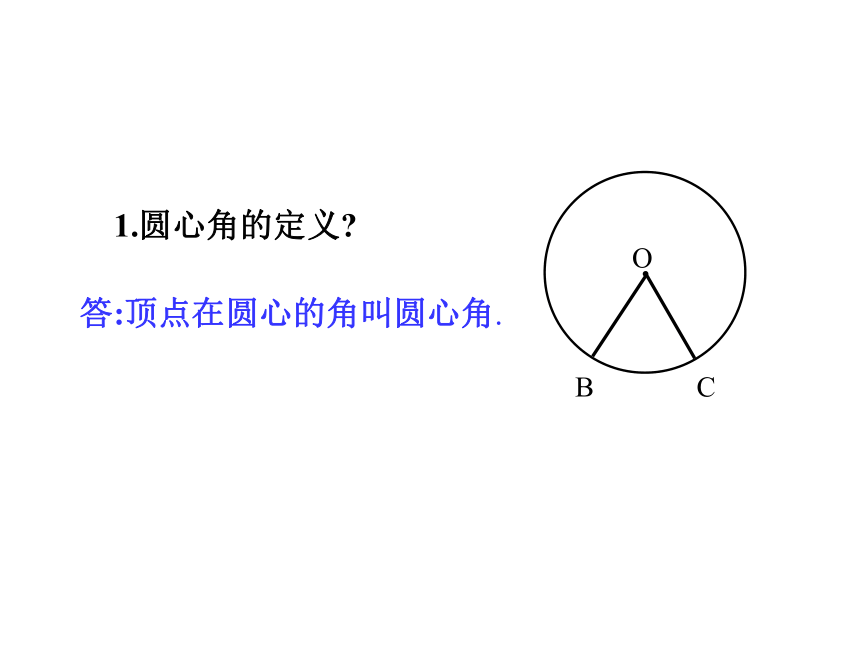
1.圆心角的定义
.
O
B
C
答:顶点在圆心的角叫圆心角.
.
O
B
C
圆心角的度数和它所对的弧的度数的关系
我们把顶点在圆心的周角等分成360份时,每一份的圆心角是1°的角。
在同圆或等圆中,圆心角的度数和它所对的弧的度数相等。
因为同圆中相等的圆心角所对的弧相等,所以整个圆也被等分成360份。我们把每一份这样的弧叫做1°的弧。
在同圆或等圆中,
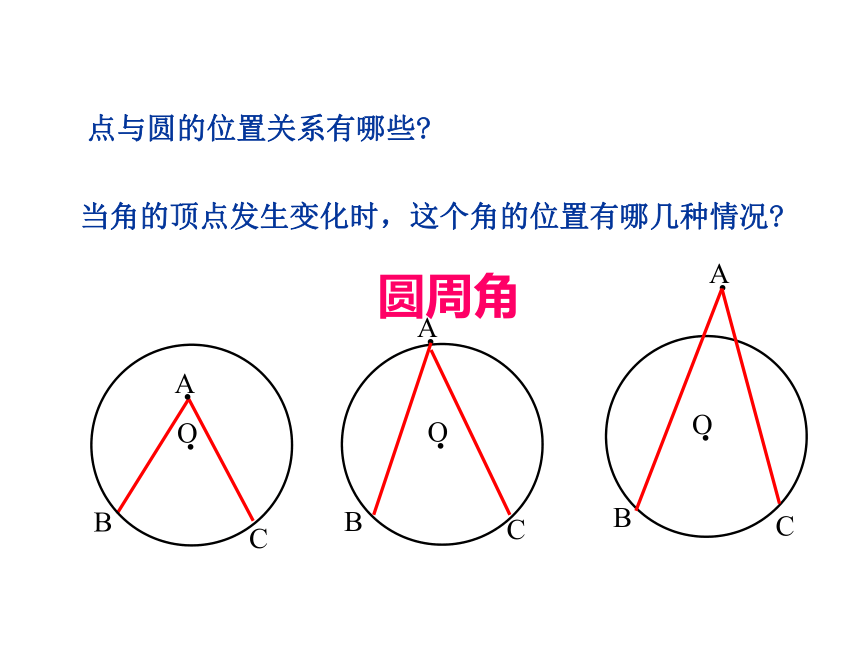
点与圆的位置关系有哪些
B
C
当角的顶点发生变化时,这个角的位置有哪几种情况
A
.
O
.
O
.
O
.
A
.
A
.
B
C
B
C
圆周角
.
O
B
C
A
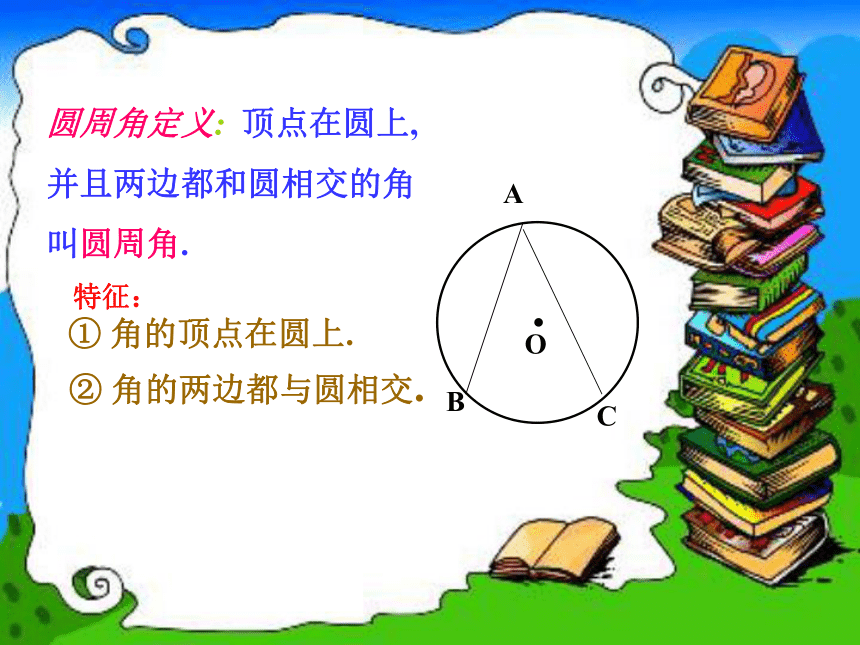
特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
圆周角定义: 顶点在圆上,
并且两边都和圆相交的角
叫圆周角.
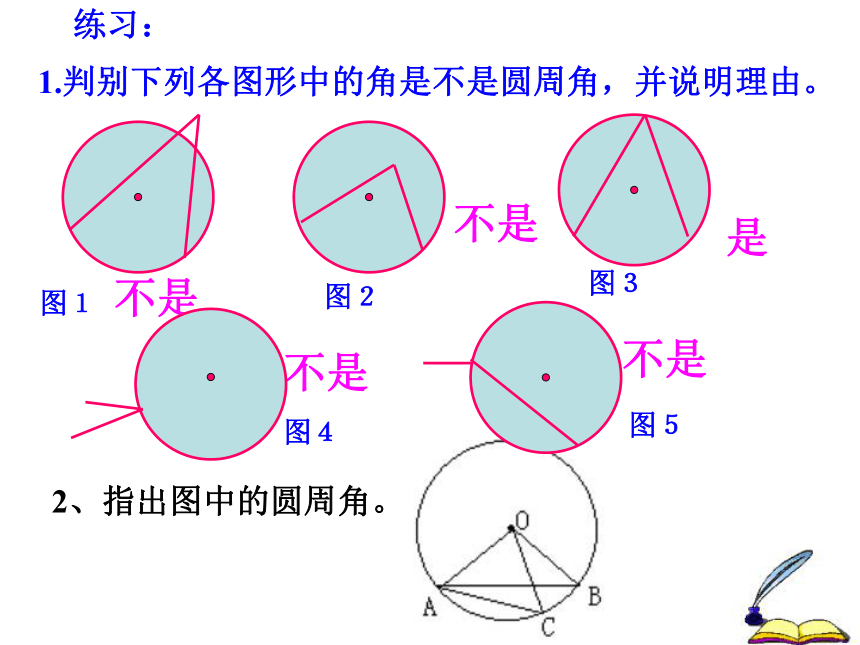
练习:
1.判别下列各图形中的角是不是圆周角,并说明理由。
不是
不是
是
不是
不是
图1
图2
图3
图4
图5
2、指出图中的圆周角。
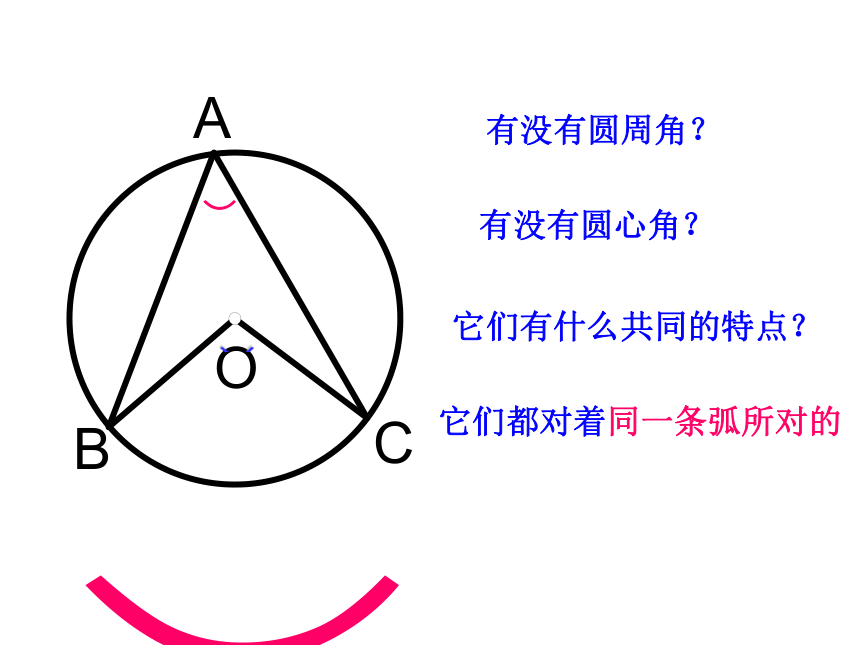
有没有圆周角?
有没有圆心角?
它们有什么共同的特点?
它们都对着同一条弧所对的
⌒
⌒
⌒
下列图形中,哪些图形中的圆心角∠BOC和圆周角∠A是同对一条弧。
自己动手量一量同一条弧所对的圆心角和圆周角分别是多少度?
一条弧所对的圆周角等于它所对的圆心角的一半
为了解决这个问题,我们先探究一条弧所对的圆
周角和圆心角之间有的关系.
类比圆心角探知圆周角
在同圆或等圆中,相等的弧所对的圆心角相等.
在同圆或等圆中,相等的弧所对的圆周角有什么关系?
想一想
●O
●O
●O
A
B
C
A
B
C
A
B
C
圆周角和圆心角的关系
如图,观察弧AC所对的圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系
说说你的想法,并与同伴交流.
议一议
教师提示:注意圆心与圆周角的位置关系.
●O
A
B
C
●O
A
B
C
●O
A
B
C
圆周角和圆心角的关系
1.首先考虑一种特殊情况:
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.
议一议
∵∠AOC是△ABO的外角,
∴∠AOC=∠B+∠A.
∵OA=OB,
●O
A
B
C
∴∠A=∠B.
∴∠AOC=2∠B.
即 ∠ABC = ∠AOC.
你能写出这个命题吗
一条弧所对的圆周角等于它所对的圆心角的一半.
老师期望:你可要理解并掌握这个模型.
圆周角和圆心角的关系
如果圆心不在圆周角的一边上,结果会怎样
2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样
议一议
老师提示:能否转化为1的情况
过点B作直径BD.由1可得:
●O
∴ ∠ABC = ∠AOC.
你能写出这个命题吗
一条弧所对的圆周角等于它所对的圆心角的一半.
A
B
C
D
∠ABD = ∠AOD,∠CBD = ∠COD,
圆周角和圆心角的关系
如果圆心不在圆周角的一边上,结果会怎样
3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样
议一议
老师提示:能否也转化为1的情况
过点B作直径BD.由1可得:
●O
∴ ∠ABC = ∠AOC.
你能写出这个命题吗
一条弧所对的圆周角等于它所对的圆心角的一半.
D
∠ABD = ∠AOD,∠CBD = ∠COD,
A
B
C
圆周角定理
综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:
圆周角定理:一条弧所对的圆周角等于它所对
的圆心角的一半.
议一议
老师提示:圆周角定理是承上启下的知识点,要予以重视.
●O
A
B
C
●O
A
B
C
●O
A
B
C
即 ∠ABC = ∠AOC.
练习:
2.如图,圆心角∠AOB=100°,则∠ACB=___。
O
A
B
C
B
A
O
.
70°
x
1.求圆中角X的度数
A
O
.
X
120°
130°
A
O
.
X
120°
C
C
D
B
3、 如图,在直径为AB的半圆中,O为圆心,C、D为半圆上的两点,∠COD=500,则∠CAD=_________
.
做做看,收获知多少?
一、判断
1、顶点在圆上的角叫圆周角。
2、圆周角的度数等于所对弧的度数的一半。
二、计算
1、半径为R的圆中,有一弦分圆周成1:2两
部分,则弦所对的圆周角的度数是 。
×
√
O
60°或120°
2、如图,在⊙O中,∠BOC=50°,
求∠A的大小.
●O
B
A
C
解: ∠A= ∠BOC = 25°.
习题1.如图:OA、OB、OC都是⊙O的半径 ∠AOB=2∠BOC.
求证:∠ACB=2∠BAC.
证明:
∠ACB= ∠AOB
1
2
∠BAC= ∠BOC
2
∠AOB=2∠BOC
A
O
B
C
∠ACB=2∠BAC
1
规律:解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理
分析:AB所对圆周角是∠ACB, 圆心角是∠AOB. 则∠ACB= ∠AOB.
BC所对圆周角是∠ BAC , 圆心角是∠BOC, 则∠ BAC= ∠BOC
⌒
⌒
2
1
___
2
1
___
习题1.如图:OA、OB、OC都是⊙O的半径 ∠AOB=2∠BOC.
求证:∠ACB=2∠BAC.
证明:
∠ACB= ∠AOB
1
2
∠BAC= ∠BOC
2
∠AOB=2∠BOC
A
O
B
C
∠ACB=2∠BAC
1
规律:解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理
分析:AB所对圆周角是∠ACB, 圆心角是∠AOB. 则∠ACB= ∠AOB.
BC所对圆周角是∠ BAC , 圆心角是∠BOC, 则∠ BAC= ∠BOC
⌒
⌒
2
1
___
2
1
___
思考题:如图,在⊙O中, CE=BD, DE=2BC, ∠ EOD=64°,求∠ A的度数。
︵
︵
A
B
C
D
E
O
一 、这节课主要学习了两个知识点:
1、圆周角定义。
2、圆周角定理及其定理应用。
二、方法上主要学习了圆周角定理的证明渗透了“特殊到一般”的思想方法和分类讨论的思想方法。
三、圆周角及圆周角定理的应用极其广泛,也是中考的一个重要考点,望同学们灵活运用
2.如图(2),在⊙O中,∠B,∠D,∠E的大小有什么关系
为什么
3.如图(3),AB是直径,你能确定∠C的度数吗
拓展 化心动为行动
1.如图(1),在⊙O中,∠BAC=50°,求∠C的大小.
猜一猜
●O
C
A
B
D
(1)
●O
B
A
C
D
E
(2)
●O
A
B
C
(3)
练习: 4、AB、AC为⊙O的两条弦,延长CA到D,使AD=AB,如果∠ADB=350,求∠BOC的度数。 5、如图,在⊙O中,BC=2DE, ∠ BOC=84°,求∠ A的度数。
⌒
⌒
3.3 圆周角和圆心角的关系(1)
大兴学校 卿丽萍
圆心角、弧、弦、弦心距之间的关系
在同圆或等圆中,
相等的圆心角所对的弧相等,
所对的弦相等
圆心角、弧、弦、弦心距之间的关系
在同圆或等圆中,
如果两个圆心角、
两条弧、
两条弦
中有一组量相等,
中有一组量相等,那么它们所对应的其余各组量都分别相等
1.圆心角的定义
.
O
B
C
答:顶点在圆心的角叫圆心角.
.
O
B
C
圆心角的度数和它所对的弧的度数的关系
我们把顶点在圆心的周角等分成360份时,每一份的圆心角是1°的角。
在同圆或等圆中,圆心角的度数和它所对的弧的度数相等。
因为同圆中相等的圆心角所对的弧相等,所以整个圆也被等分成360份。我们把每一份这样的弧叫做1°的弧。
在同圆或等圆中,
点与圆的位置关系有哪些
B
C
当角的顶点发生变化时,这个角的位置有哪几种情况
A
.
O
.
O
.
O
.
A
.
A
.
B
C
B
C
圆周角
.
O
B
C
A
特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
圆周角定义: 顶点在圆上,
并且两边都和圆相交的角
叫圆周角.
练习:
1.判别下列各图形中的角是不是圆周角,并说明理由。
不是
不是
是
不是
不是
图1
图2
图3
图4
图5
2、指出图中的圆周角。
有没有圆周角?
有没有圆心角?
它们有什么共同的特点?
它们都对着同一条弧所对的
⌒
⌒
⌒
下列图形中,哪些图形中的圆心角∠BOC和圆周角∠A是同对一条弧。
自己动手量一量同一条弧所对的圆心角和圆周角分别是多少度?
一条弧所对的圆周角等于它所对的圆心角的一半
为了解决这个问题,我们先探究一条弧所对的圆
周角和圆心角之间有的关系.
类比圆心角探知圆周角
在同圆或等圆中,相等的弧所对的圆心角相等.
在同圆或等圆中,相等的弧所对的圆周角有什么关系?
想一想
●O
●O
●O
A
B
C
A
B
C
A
B
C
圆周角和圆心角的关系
如图,观察弧AC所对的圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系
说说你的想法,并与同伴交流.
议一议
教师提示:注意圆心与圆周角的位置关系.
●O
A
B
C
●O
A
B
C
●O
A
B
C
圆周角和圆心角的关系
1.首先考虑一种特殊情况:
当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系.
议一议
∵∠AOC是△ABO的外角,
∴∠AOC=∠B+∠A.
∵OA=OB,
●O
A
B
C
∴∠A=∠B.
∴∠AOC=2∠B.
即 ∠ABC = ∠AOC.
你能写出这个命题吗
一条弧所对的圆周角等于它所对的圆心角的一半.
老师期望:你可要理解并掌握这个模型.
圆周角和圆心角的关系
如果圆心不在圆周角的一边上,结果会怎样
2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样
议一议
老师提示:能否转化为1的情况
过点B作直径BD.由1可得:
●O
∴ ∠ABC = ∠AOC.
你能写出这个命题吗
一条弧所对的圆周角等于它所对的圆心角的一半.
A
B
C
D
∠ABD = ∠AOD,∠CBD = ∠COD,
圆周角和圆心角的关系
如果圆心不在圆周角的一边上,结果会怎样
3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样
议一议
老师提示:能否也转化为1的情况
过点B作直径BD.由1可得:
●O
∴ ∠ABC = ∠AOC.
你能写出这个命题吗
一条弧所对的圆周角等于它所对的圆心角的一半.
D
∠ABD = ∠AOD,∠CBD = ∠COD,
A
B
C
圆周角定理
综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:
圆周角定理:一条弧所对的圆周角等于它所对
的圆心角的一半.
议一议
老师提示:圆周角定理是承上启下的知识点,要予以重视.
●O
A
B
C
●O
A
B
C
●O
A
B
C
即 ∠ABC = ∠AOC.
练习:
2.如图,圆心角∠AOB=100°,则∠ACB=___。
O
A
B
C
B
A
O
.
70°
x
1.求圆中角X的度数
A
O
.
X
120°
130°
A
O
.
X
120°
C
C
D
B
3、 如图,在直径为AB的半圆中,O为圆心,C、D为半圆上的两点,∠COD=500,则∠CAD=_________
.
做做看,收获知多少?
一、判断
1、顶点在圆上的角叫圆周角。
2、圆周角的度数等于所对弧的度数的一半。
二、计算
1、半径为R的圆中,有一弦分圆周成1:2两
部分,则弦所对的圆周角的度数是 。
×
√
O
60°或120°
2、如图,在⊙O中,∠BOC=50°,
求∠A的大小.
●O
B
A
C
解: ∠A= ∠BOC = 25°.
习题1.如图:OA、OB、OC都是⊙O的半径 ∠AOB=2∠BOC.
求证:∠ACB=2∠BAC.
证明:
∠ACB= ∠AOB
1
2
∠BAC= ∠BOC
2
∠AOB=2∠BOC
A
O
B
C
∠ACB=2∠BAC
1
规律:解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理
分析:AB所对圆周角是∠ACB, 圆心角是∠AOB. 则∠ACB= ∠AOB.
BC所对圆周角是∠ BAC , 圆心角是∠BOC, 则∠ BAC= ∠BOC
⌒
⌒
2
1
___
2
1
___
习题1.如图:OA、OB、OC都是⊙O的半径 ∠AOB=2∠BOC.
求证:∠ACB=2∠BAC.
证明:
∠ACB= ∠AOB
1
2
∠BAC= ∠BOC
2
∠AOB=2∠BOC
A
O
B
C
∠ACB=2∠BAC
1
规律:解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理
分析:AB所对圆周角是∠ACB, 圆心角是∠AOB. 则∠ACB= ∠AOB.
BC所对圆周角是∠ BAC , 圆心角是∠BOC, 则∠ BAC= ∠BOC
⌒
⌒
2
1
___
2
1
___
思考题:如图,在⊙O中, CE=BD, DE=2BC, ∠ EOD=64°,求∠ A的度数。
︵
︵
A
B
C
D
E
O
一 、这节课主要学习了两个知识点:
1、圆周角定义。
2、圆周角定理及其定理应用。
二、方法上主要学习了圆周角定理的证明渗透了“特殊到一般”的思想方法和分类讨论的思想方法。
三、圆周角及圆周角定理的应用极其广泛,也是中考的一个重要考点,望同学们灵活运用
2.如图(2),在⊙O中,∠B,∠D,∠E的大小有什么关系
为什么
3.如图(3),AB是直径,你能确定∠C的度数吗
拓展 化心动为行动
1.如图(1),在⊙O中,∠BAC=50°,求∠C的大小.
猜一猜
●O
C
A
B
D
(1)
●O
B
A
C
D
E
(2)
●O
A
B
C
(3)
练习: 4、AB、AC为⊙O的两条弦,延长CA到D,使AD=AB,如果∠ADB=350,求∠BOC的度数。 5、如图,在⊙O中,BC=2DE, ∠ BOC=84°,求∠ A的度数。
⌒
⌒
