2021-2022学年苏科新版八年级上册数学第2章 轴对称图形单元测试卷(word解析版)
文档属性
| 名称 | 2021-2022学年苏科新版八年级上册数学第2章 轴对称图形单元测试卷(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 346.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 12:55:39 | ||
图片预览

文档简介
2021-2022学年苏科新版八年级上册数学《第2章
轴对称图形》单元测试卷
一.选择题
1.如图所示,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,DE=4,BC=9,则BD的长为( )
A.6
B.5
C.4
D.3
2.如图,一个经过改造的台球桌面上四个角的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入( )球袋.
A.1号
B.2号
C.3号
D.4号
3.室内墙壁上挂一平面镜,小明在平面镜内看到他背后墙上时钟的示数如图所示,则这时的实际时间应是( )
A.3:40
B.8:20
C.3:20
D.4:20
4.下列说法正确的是( )
A.能够完全重合的两个图形成轴对称
B.全等的两个图形成轴对称
C.形状一样的两个图形成轴对称
D.沿着一条直线对折能够重合的两个图形成轴对称
5.如图,在一个规格为6×12(即6×12个小正方形)的球台上,有两个小球A,B.若击打小球A,经过球台边的反弹后,恰好击中小球B,那么小球A击出时,应瞄准球台边上的点( )
A.P1
B.P2
C.P3
D.P4
6.下列图案属于轴对称图案的是( )
A.
B.
C.
D.
7.如图的2×4的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与△ABC成轴对称的格点三角形一共有( )
A.2个
B.3个
C.4个
D.5个
8.黄帅拿一张正方形的纸按如图所示沿虚线连续对折后剪去带直角的部分,然后打开后的形状是( )
A.
B.
C.
D.
9.如图①,一张四边形纸片ABCD,∠A=50°,∠C=150°.若将其按照图②所示方式折叠后,恰好MD′∥AB,ND′∥BC,则∠D的度数为( )
A.70°
B.75°
C.80°
D.85°
10.如图,分别以△ABC的边AB,AC所在直线为对称轴作△ABC的对称图形△ABD和△ACE,∠BAC=150°,线段BD与CE相交于点O,连接BE、ED、DC、OA.有如下结论:①∠EAD=90°;②∠BOE=60°;③OA平分∠BOC;④EA=ED;⑤BP=EQ.其中正确的结论个数是( )
A.4个
B.3个
C.2个
D.1个
二.填空题
11.正方形是轴对称图形,它共有
条对称轴.
12.如图,∠1=∠2,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时必须保证∠1为
°.
13.如图a是长方形纸带,∠DEF=26°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是
.
14.如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则△ABC的周长为
.
15.如图是一个经过改造的台球桌面的示意图,图中四个角上的黑色部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多次反弹),那么该球最后将落入的球袋是
号袋(填球袋的编号).
16.从数学对称的角度看,下面的几组大写英文字母:①ANEC;②KBSM;③XIHZ;④ZDWH,不同于另外一组的是
.
17.在上学的路上,小刚从电瓶车的后视镜里看到一辆汽车,车顶字牌上的字在平面镜中的像是IXAT,则这辆车车顶字牌上的字实际是
.
18.如图,将一张正方形纸片,第1次剪成四个大小形状一样的小正方形,第2次将其中的一个小正方形再按同样的方法剪成四个小正方形,然后再将其中的一个小正方形剪成四个小正方形,如此循环进行下去,如果共剪n次,则可剪出
个正方形.
19.如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点,若∠MON=40°,则∠GOH=
.
20.如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且以格占为顶点的三角形,这样的三角形共有
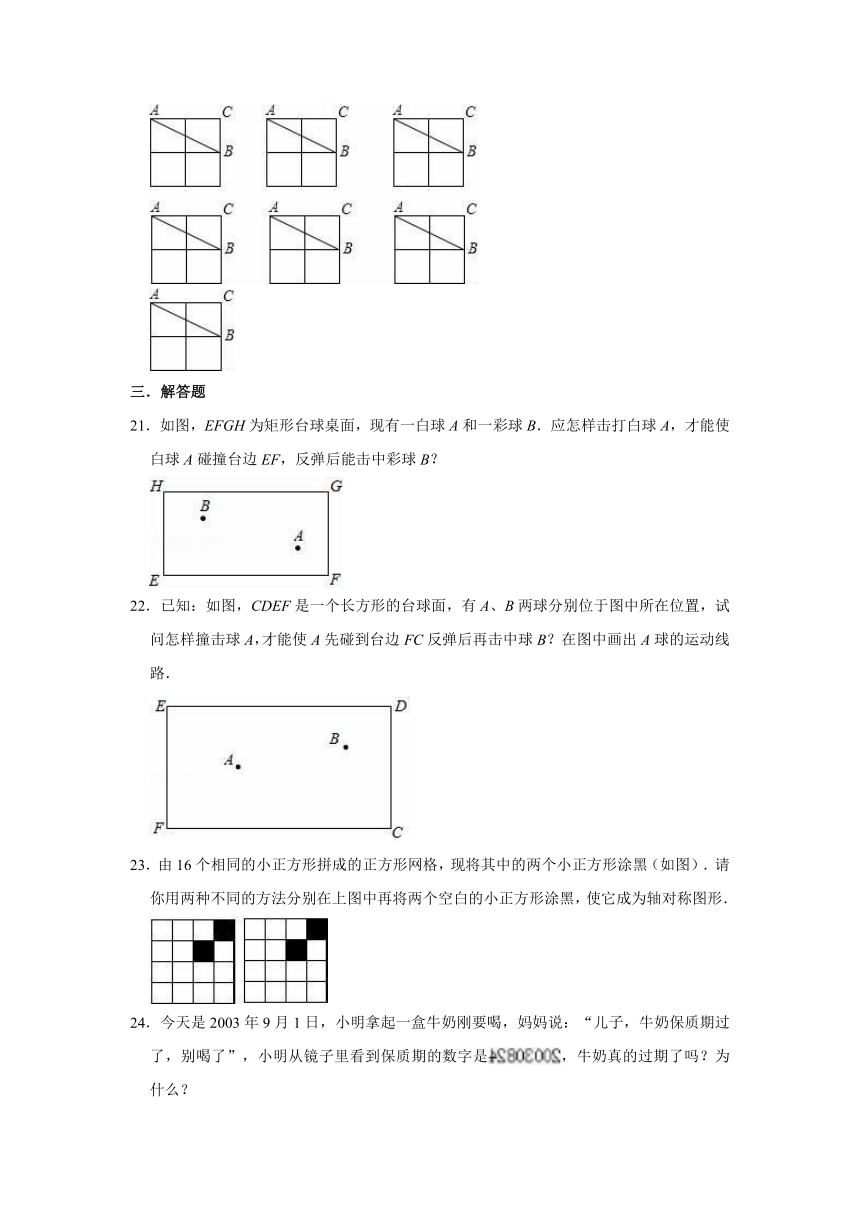
个,请在下面所给的格纸中一一画出.(所给的六个格纸未必全用).
三.解答题
21.如图,EFGH为矩形台球桌面,现有一白球A和一彩球B.应怎样击打白球A,才能使白球A碰撞台边EF,反弹后能击中彩球B?
22.已知:如图,CDEF是一个长方形的台球面,有A、B两球分别位于图中所在位置,试问怎样撞击球A,才能使A先碰到台边FC反弹后再击中球B?在图中画出A球的运动线路.
23.由16个相同的小正方形拼成的正方形网格,现将其中的两个小正方形涂黑(如图).请你用两种不同的方法分别在上图中再将两个空白的小正方形涂黑,使它成为轴对称图形.
24.今天是2003年9月1日,小明拿起一盒牛奶刚要喝,妈妈说:“儿子,牛奶保质期过了,别喝了”,小明从镜子里看到保质期的数字是,牛奶真的过期了吗?为什么?
25.如图,P在∠AOB内,点M,N分别是点P关于AO,BO的对称点,且与AO、BO相交点E、F,若△PEF的周长为15,求MN的长.
26.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)请你判断AE、AF与BE之间的数量关系,并说明理由.
27.如图:已知,P为∠AOB内一点,分别作出点P关于OA,OB的对称点P1,P2,连P1P2交OA于M,交OB于N,若P1P2=5cm,求△PMN的周长.
参考答案与试题解析
一.选择题
1.解:∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DC=DE=4,
∴BD=BC﹣CD=9﹣4=5.
故选:B.
2.解:根据题意:每次反射,都成轴对称变化,
∴一个球按图中所示的方向被击出,经过3次反射后,落入1号球袋.
故选:A.
3.解:根据镜面对称的性质,分析可得题中所显示的时刻与3:40成轴对称,所以此时实际时刻为3:40.
故选:A.
4.解:A、能够完全重合的两个图形叫做全等形,故此选项错误;
B、C、如右图可知,此两个选项错误;
D、沿着一条直线对折能够重合的两个图形成轴对称,此选项正确;
故选:D.
5.解:如图,应瞄准球台边上的点是P2.
故选:B.
6.解:A、是轴对称图形,故此选项正确;
B、不是轴对称图形,故此选项错误;
C、不是轴对称图形,故此选项错误;
D、不是轴对称图形,故此选项错误;
故选:A.
7.解:如图所示,对称轴有三种位置,与△ABC成轴对称的格点三角形有3个.
故选B.
8.解:严格按照图中的顺序向右下对折,向左下对折,从直角顶点处剪去一个直角三角形,展开得到结论.故选C.
9.解:∵△MND′由△MND翻折而成,
∴∠1=∠D′MN,∠2=∠D′NM,
∵MD′∥AB,ND′∥BC,∠A=50°,∠C=150°
∴∠1+∠D′MN=∠A=50°,∠2+∠D′NM=∠C=150°,
∴∠1=∠D′MN===25°,∠2=∠D′NM===75°,
∴∠D=180°﹣∠1﹣∠2=180°﹣25°﹣75°=80°.
故选:C.
10.解:∵△ABD和△ACE是△ABC的轴对称图形,
∴∠BAD=∠CAE=∠BAC,AB=AE,AC=AD,
∴∠EAD=3∠BAC﹣360°=3×150°﹣360°=90°,故①正确;
∴∠BAE=∠CAD=(360°﹣90°﹣150°)=60°,
由翻折的性质得,∠AEC=∠ABD=∠ABC,
又∵∠EPO=∠BPA,
∴∠BOE=∠BAE=60°,故②正确;
∵△ACE≌△ADB,
∴S△ACE=S△ADB,BD=CE,
∴BD边上的高与CE边上的高相等,
即点A到∠BOC两边的距离相等,
∴OA平分∠BOC,故③正确;
只有当AC=AB时,∠ADE=30°,才有EA=ED,故④错误;
在△ABP和△AEQ中,∠ABD=∠AEC,AB=AE,∠BAE=60°,∠EAQ=90°,
∴BP<EQ,故⑤错误;
综上所述,结论正确的是①②③共3个.
故选:B.
二.填空题
11.解:∵如图所示,正方形是轴对称图形,它共有4条对称轴.
故答案为:4.
12.解:要使白球反弹后能将黑球直接撞入袋中,
∠2+∠3=90°,
∴∠2=60°,
∵∠1=∠2,
∴∠1=60°.
13.解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠BFE=∠DEF=26°,
∴∠CFE=∠CFG﹣∠EFG=180°﹣2∠BFE﹣∠EFG=180°﹣3×26°=102°,
故答案为:102°.
14.解:∵∠C=90°,∠C=30°,
∴∠CAB=60°,
∵AD平分∠CAB,
∴∠CAD=∠DAB=∠B=30°,
∴DA=DB,
∵DE⊥AB,
∴AE=BE==,
∴AB=2,
∵AC=AB,
∴AC=,
∴BC==3,
∴△ABC的周长为+2+3=3+3,
故答案为3+3.
15.解:如图所示,则该球最后将落入的球袋是3号袋.
故答案为:3.
16.解:③XIHZ中全是中心对称;
所以而其它选项都有一个以上非中心对称图形.
故应填③.
17.解:IXAT是经过镜子反射后的字母,则这车车顶上字牌上的字实际是TAXI.
故答案为TAXI.
18.解:根据题意可知:后一个图形中的个数总比前一个图形中的个数多3个,
即剪第1次时,可剪出4个正方形;
剪第2次时,可剪出7个正方形;
剪第3次时,可剪出10个正方形;
剪第4次时,可剪出13个正方形;
…
剪n次时,共剪出小正方形的个数为:4+3(n﹣1)=3n+1.
故答案为:3n+1.
19.解:如图,连接OP,
∵P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,
∴∠GOM=∠MOP,∠PON=∠NOH,
∴∠GOH=∠GOM+∠MOP+∠PON+∠NOH=2∠MON,
∵∠MON=40°,
∴∠GOH=2×40°=80°.
故答案为:80°.
20.解:与△ABC成轴对称且以格点为顶点的三角形如图:
共5个.
三.解答题
21.解:如图,作点A关于EF的对称点A′,连接A′B,交EF于点C,将白球A打到台边EF的点C处,反弹后能击中彩球B.
22.解:如图所示:运动路线:A→P→B.
23.解:
24.解:
|20030824,
∴实际的保质期应是20030824,故牛奶已经过期.
25.解:∵点M是点P关于AO,的对称点,
∴AO垂直平分MP,
∴EP=EM.
同理PF=FN.
∵MN=ME+EF+FN,
∴MN=EP+EF+PF,
∵△PEF的周长为15,
∴MN=EP+EF+PF=15.
26.证明:(1)∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴DC=DE,
在Rt△DCF和Rt△DEB中,
,
∴Rt△DCF≌Rt△DEB,
∴CF=EB;
(2)AF+BE=AE.
∵Rt△DCF≌Rt△DEB,
∴AC=AE,
∴AF+FC=AE,
即AF+BE=AE.
27.解:∵P点关于OA的对称是点P1,P点关于OB的对称点P2,
∴PM=P1M,PN=P2N,
∴△PMN的周长=PM+PN+MN=MN+P1M+P2N=P1P2=5cm.
轴对称图形》单元测试卷
一.选择题
1.如图所示,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,DE=4,BC=9,则BD的长为( )
A.6
B.5
C.4
D.3
2.如图,一个经过改造的台球桌面上四个角的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入( )球袋.
A.1号
B.2号
C.3号
D.4号
3.室内墙壁上挂一平面镜,小明在平面镜内看到他背后墙上时钟的示数如图所示,则这时的实际时间应是( )
A.3:40
B.8:20
C.3:20
D.4:20
4.下列说法正确的是( )
A.能够完全重合的两个图形成轴对称
B.全等的两个图形成轴对称
C.形状一样的两个图形成轴对称
D.沿着一条直线对折能够重合的两个图形成轴对称
5.如图,在一个规格为6×12(即6×12个小正方形)的球台上,有两个小球A,B.若击打小球A,经过球台边的反弹后,恰好击中小球B,那么小球A击出时,应瞄准球台边上的点( )
A.P1
B.P2
C.P3
D.P4
6.下列图案属于轴对称图案的是( )
A.
B.
C.
D.
7.如图的2×4的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与△ABC成轴对称的格点三角形一共有( )
A.2个
B.3个
C.4个
D.5个
8.黄帅拿一张正方形的纸按如图所示沿虚线连续对折后剪去带直角的部分,然后打开后的形状是( )
A.
B.
C.
D.
9.如图①,一张四边形纸片ABCD,∠A=50°,∠C=150°.若将其按照图②所示方式折叠后,恰好MD′∥AB,ND′∥BC,则∠D的度数为( )
A.70°
B.75°
C.80°
D.85°
10.如图,分别以△ABC的边AB,AC所在直线为对称轴作△ABC的对称图形△ABD和△ACE,∠BAC=150°,线段BD与CE相交于点O,连接BE、ED、DC、OA.有如下结论:①∠EAD=90°;②∠BOE=60°;③OA平分∠BOC;④EA=ED;⑤BP=EQ.其中正确的结论个数是( )
A.4个
B.3个
C.2个
D.1个
二.填空题
11.正方形是轴对称图形,它共有
条对称轴.
12.如图,∠1=∠2,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时必须保证∠1为
°.
13.如图a是长方形纸带,∠DEF=26°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是
.
14.如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则△ABC的周长为
.
15.如图是一个经过改造的台球桌面的示意图,图中四个角上的黑色部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多次反弹),那么该球最后将落入的球袋是
号袋(填球袋的编号).
16.从数学对称的角度看,下面的几组大写英文字母:①ANEC;②KBSM;③XIHZ;④ZDWH,不同于另外一组的是
.
17.在上学的路上,小刚从电瓶车的后视镜里看到一辆汽车,车顶字牌上的字在平面镜中的像是IXAT,则这辆车车顶字牌上的字实际是
.
18.如图,将一张正方形纸片,第1次剪成四个大小形状一样的小正方形,第2次将其中的一个小正方形再按同样的方法剪成四个小正方形,然后再将其中的一个小正方形剪成四个小正方形,如此循环进行下去,如果共剪n次,则可剪出
个正方形.
19.如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点,若∠MON=40°,则∠GOH=
.
20.如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且以格占为顶点的三角形,这样的三角形共有
个,请在下面所给的格纸中一一画出.(所给的六个格纸未必全用).
三.解答题
21.如图,EFGH为矩形台球桌面,现有一白球A和一彩球B.应怎样击打白球A,才能使白球A碰撞台边EF,反弹后能击中彩球B?
22.已知:如图,CDEF是一个长方形的台球面,有A、B两球分别位于图中所在位置,试问怎样撞击球A,才能使A先碰到台边FC反弹后再击中球B?在图中画出A球的运动线路.
23.由16个相同的小正方形拼成的正方形网格,现将其中的两个小正方形涂黑(如图).请你用两种不同的方法分别在上图中再将两个空白的小正方形涂黑,使它成为轴对称图形.
24.今天是2003年9月1日,小明拿起一盒牛奶刚要喝,妈妈说:“儿子,牛奶保质期过了,别喝了”,小明从镜子里看到保质期的数字是,牛奶真的过期了吗?为什么?
25.如图,P在∠AOB内,点M,N分别是点P关于AO,BO的对称点,且与AO、BO相交点E、F,若△PEF的周长为15,求MN的长.
26.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)请你判断AE、AF与BE之间的数量关系,并说明理由.
27.如图:已知,P为∠AOB内一点,分别作出点P关于OA,OB的对称点P1,P2,连P1P2交OA于M,交OB于N,若P1P2=5cm,求△PMN的周长.
参考答案与试题解析
一.选择题
1.解:∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DC=DE=4,
∴BD=BC﹣CD=9﹣4=5.
故选:B.
2.解:根据题意:每次反射,都成轴对称变化,
∴一个球按图中所示的方向被击出,经过3次反射后,落入1号球袋.
故选:A.
3.解:根据镜面对称的性质,分析可得题中所显示的时刻与3:40成轴对称,所以此时实际时刻为3:40.
故选:A.
4.解:A、能够完全重合的两个图形叫做全等形,故此选项错误;
B、C、如右图可知,此两个选项错误;
D、沿着一条直线对折能够重合的两个图形成轴对称,此选项正确;
故选:D.
5.解:如图,应瞄准球台边上的点是P2.
故选:B.
6.解:A、是轴对称图形,故此选项正确;
B、不是轴对称图形,故此选项错误;
C、不是轴对称图形,故此选项错误;
D、不是轴对称图形,故此选项错误;
故选:A.
7.解:如图所示,对称轴有三种位置,与△ABC成轴对称的格点三角形有3个.
故选B.
8.解:严格按照图中的顺序向右下对折,向左下对折,从直角顶点处剪去一个直角三角形,展开得到结论.故选C.
9.解:∵△MND′由△MND翻折而成,
∴∠1=∠D′MN,∠2=∠D′NM,
∵MD′∥AB,ND′∥BC,∠A=50°,∠C=150°
∴∠1+∠D′MN=∠A=50°,∠2+∠D′NM=∠C=150°,
∴∠1=∠D′MN===25°,∠2=∠D′NM===75°,
∴∠D=180°﹣∠1﹣∠2=180°﹣25°﹣75°=80°.
故选:C.
10.解:∵△ABD和△ACE是△ABC的轴对称图形,
∴∠BAD=∠CAE=∠BAC,AB=AE,AC=AD,
∴∠EAD=3∠BAC﹣360°=3×150°﹣360°=90°,故①正确;
∴∠BAE=∠CAD=(360°﹣90°﹣150°)=60°,
由翻折的性质得,∠AEC=∠ABD=∠ABC,
又∵∠EPO=∠BPA,
∴∠BOE=∠BAE=60°,故②正确;
∵△ACE≌△ADB,
∴S△ACE=S△ADB,BD=CE,
∴BD边上的高与CE边上的高相等,
即点A到∠BOC两边的距离相等,
∴OA平分∠BOC,故③正确;
只有当AC=AB时,∠ADE=30°,才有EA=ED,故④错误;
在△ABP和△AEQ中,∠ABD=∠AEC,AB=AE,∠BAE=60°,∠EAQ=90°,
∴BP<EQ,故⑤错误;
综上所述,结论正确的是①②③共3个.
故选:B.
二.填空题
11.解:∵如图所示,正方形是轴对称图形,它共有4条对称轴.
故答案为:4.
12.解:要使白球反弹后能将黑球直接撞入袋中,
∠2+∠3=90°,
∴∠2=60°,
∵∠1=∠2,
∴∠1=60°.
13.解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠BFE=∠DEF=26°,
∴∠CFE=∠CFG﹣∠EFG=180°﹣2∠BFE﹣∠EFG=180°﹣3×26°=102°,
故答案为:102°.
14.解:∵∠C=90°,∠C=30°,
∴∠CAB=60°,
∵AD平分∠CAB,
∴∠CAD=∠DAB=∠B=30°,
∴DA=DB,
∵DE⊥AB,
∴AE=BE==,
∴AB=2,
∵AC=AB,
∴AC=,
∴BC==3,
∴△ABC的周长为+2+3=3+3,
故答案为3+3.
15.解:如图所示,则该球最后将落入的球袋是3号袋.
故答案为:3.
16.解:③XIHZ中全是中心对称;
所以而其它选项都有一个以上非中心对称图形.
故应填③.
17.解:IXAT是经过镜子反射后的字母,则这车车顶上字牌上的字实际是TAXI.
故答案为TAXI.
18.解:根据题意可知:后一个图形中的个数总比前一个图形中的个数多3个,
即剪第1次时,可剪出4个正方形;
剪第2次时,可剪出7个正方形;
剪第3次时,可剪出10个正方形;
剪第4次时,可剪出13个正方形;
…
剪n次时,共剪出小正方形的个数为:4+3(n﹣1)=3n+1.
故答案为:3n+1.
19.解:如图,连接OP,
∵P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,
∴∠GOM=∠MOP,∠PON=∠NOH,
∴∠GOH=∠GOM+∠MOP+∠PON+∠NOH=2∠MON,
∵∠MON=40°,
∴∠GOH=2×40°=80°.
故答案为:80°.
20.解:与△ABC成轴对称且以格点为顶点的三角形如图:
共5个.
三.解答题
21.解:如图,作点A关于EF的对称点A′,连接A′B,交EF于点C,将白球A打到台边EF的点C处,反弹后能击中彩球B.
22.解:如图所示:运动路线:A→P→B.
23.解:
24.解:
|20030824,
∴实际的保质期应是20030824,故牛奶已经过期.
25.解:∵点M是点P关于AO,的对称点,
∴AO垂直平分MP,
∴EP=EM.
同理PF=FN.
∵MN=ME+EF+FN,
∴MN=EP+EF+PF,
∵△PEF的周长为15,
∴MN=EP+EF+PF=15.
26.证明:(1)∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴DC=DE,
在Rt△DCF和Rt△DEB中,
,
∴Rt△DCF≌Rt△DEB,
∴CF=EB;
(2)AF+BE=AE.
∵Rt△DCF≌Rt△DEB,
∴AC=AE,
∴AF+FC=AE,
即AF+BE=AE.
27.解:∵P点关于OA的对称是点P1,P点关于OB的对称点P2,
∴PM=P1M,PN=P2N,
∴△PMN的周长=PM+PN+MN=MN+P1M+P2N=P1P2=5cm.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
