2021-2022学年苏科新版九年级上册数学第2章 对称图形——圆单元测试卷(word解析版)
文档属性
| 名称 | 2021-2022学年苏科新版九年级上册数学第2章 对称图形——圆单元测试卷(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 342.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-11 12:57:53 | ||
图片预览


文档简介
2021-2022学年苏科新版九年级上册数学《第2章
对称图形——圆》单元测试卷
一.选择题
1.在⊙O中,圆心角∠AOB=90°,点O到弦AB的距离为4,则⊙O的直径的长为( )
A.
B.
C.24
D.16
2.已知⊙O半径为3,A为线段PO的中点,则当OP=6时,点A与⊙O的位置关系为( )
A.点在圆内
B.点在圆上
C.点在圆外
D.不能确定
3.下列条件中,能确定圆的是( )
A.以已知点O为圆心
B.以1cm长为半径
C.经过已知点A,且半径为2cm
D.以点O为圆心,1cm为半径
4.下列语句,错误的是( )
A.直径是弦
B.相等的圆心角所对的弧相等
C.弦的垂直平分线一定经过圆心
D.平分弧的半径垂直于弧所对的弦
5.如图,四边形PAOB是扇形OMN的内接矩形,顶点P在弧MN上,且不与M,N重合,当P点在弧MN上移动时,矩形PAOB的形状、大小随之变化,则PA2+PB2的值( )
A.变大
B.变小
C.不变
D.不能确定
6.如图,⊙O的直径CD=20,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )
A.8
B.12
C.16
D.2
7.如图,⊙O的直径CD=12cm,AB是⊙O的弦,AB⊥CD,垂足为E,OE:OC=1:3,则AB的长为( )
A.2cm
B.4cm
C.6cm
D.8cm
8.如图,A,B,C是⊙O上的三点,AB,AC的圆心O的两侧,若∠ABO=20°,∠ACO=30°,则∠BOC的度数为( )
A.100°
B.110°
C.125°
D.130°
9.如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,AB=40m,点C是的中点,点D是AB的中点,且CD=10m,则这段弯路所在圆的半径为( )
A.25m
B.24m
C.30m
D.60m
10.给定下列图形可以确定一个圆的是( )
A.已知圆心
B.已知半径
C.已知直径
D.已知三个点
二.填空题
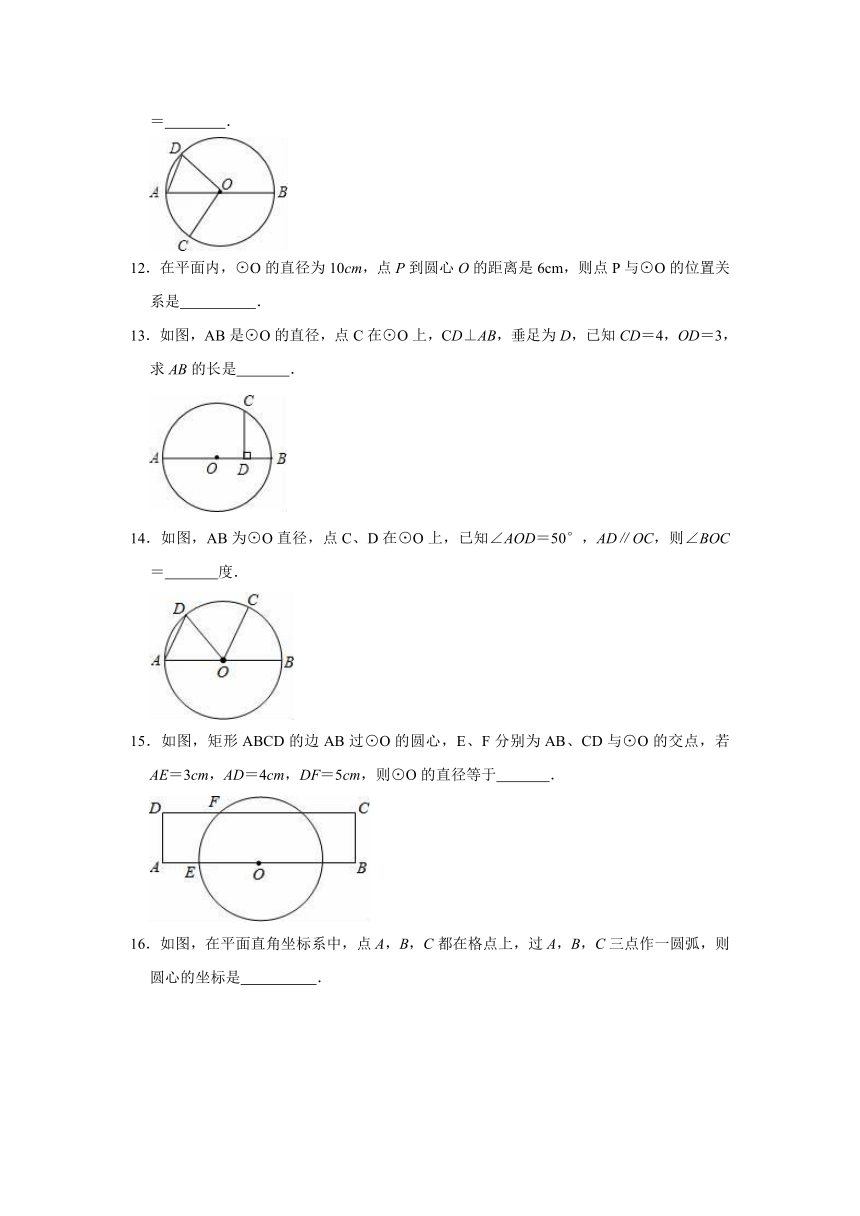
11.如图,AB是⊙O的直径,点C、D在⊙O上,∠BOC=110°,AD∥OC,则∠AOD=
.
12.在平面内,⊙O的直径为10cm,点P到圆心O的距离是6cm,则点P与⊙O的位置关系是
.
13.如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D,已知CD=4,OD=3,求AB的长是
.
14.如图,AB为⊙O直径,点C、D在⊙O上,已知∠AOD=50°,AD∥OC,则∠BOC=
度.
15.如图,矩形ABCD的边AB过⊙O的圆心,E、F分别为AB、CD与⊙O的交点,若AE=3cm,AD=4cm,DF=5cm,则⊙O的直径等于
.
16.如图,在平面直角坐标系中,点A,B,C都在格点上,过A,B,C三点作一圆弧,则圆心的坐标是
.
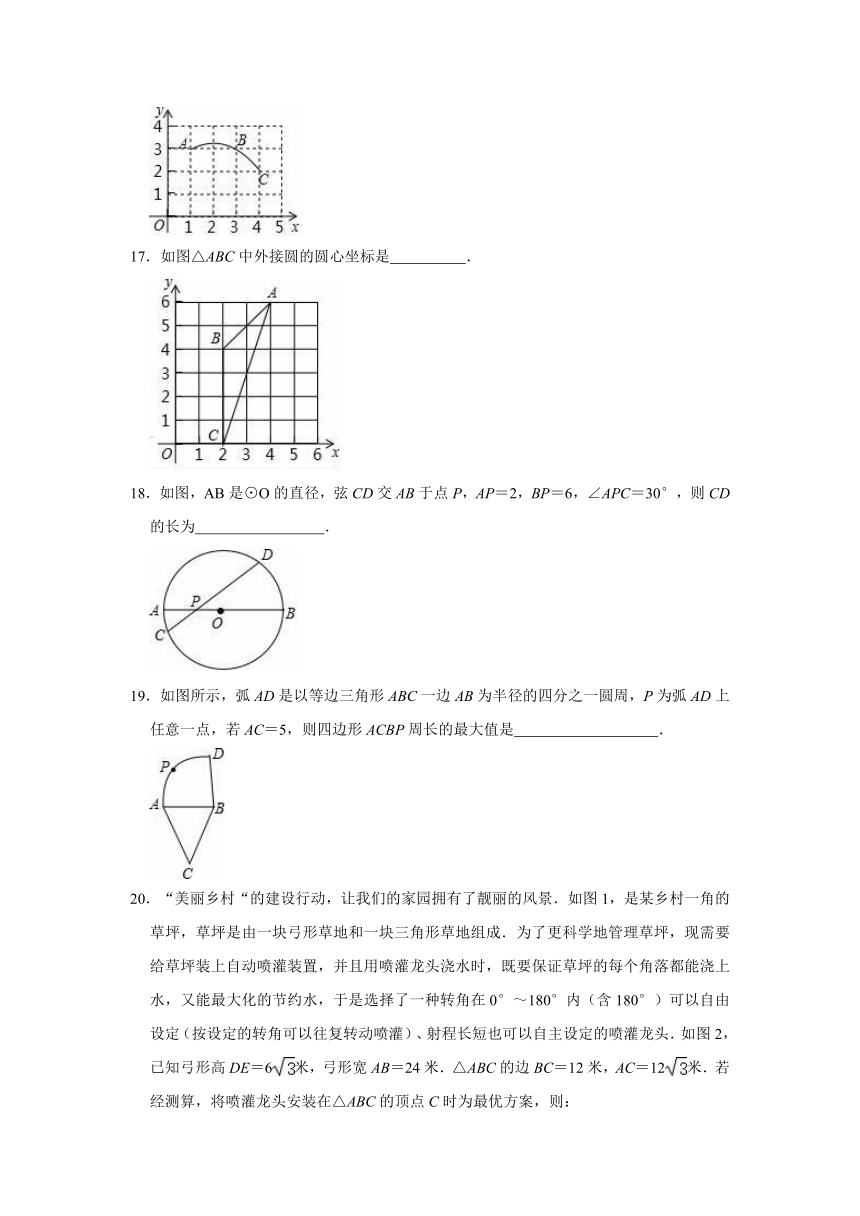
17.如图△ABC中外接圆的圆心坐标是
.
18.如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为
.
19.如图所示,弧AD是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧AD上任意一点,若AC=5,则四边形ACBP周长的最大值是
.
20.“美丽乡村“的建设行动,让我们的家园拥有了靓丽的风景.如图1,是某乡村一角的草坪,草坪是由一块弓形草地和一块三角形草地组成.为了更科学地管理草坪,现需要给草坪装上自动喷灌装置,并且用喷灌龙头浇水时,既要保证草坪的每个角落都能浇上水,又能最大化的节约水,于是选择了一种转角在0°~180°内(含180°)可以自由设定(按设定的转角可以往复转动喷灌)、射程长短也可以自主设定的喷灌龙头.如图2,已知弓形高DE=6米,弓形宽AB=24米.△ABC的边BC=12米,AC=12米.若经测算,将喷灌龙头安装在△ABC的顶点C时为最优方案,则:
(1)喷灌龙头的最小转角应设置为
度;
(2)喷灌龙头的最短射程应设置为
米.
三.解答题
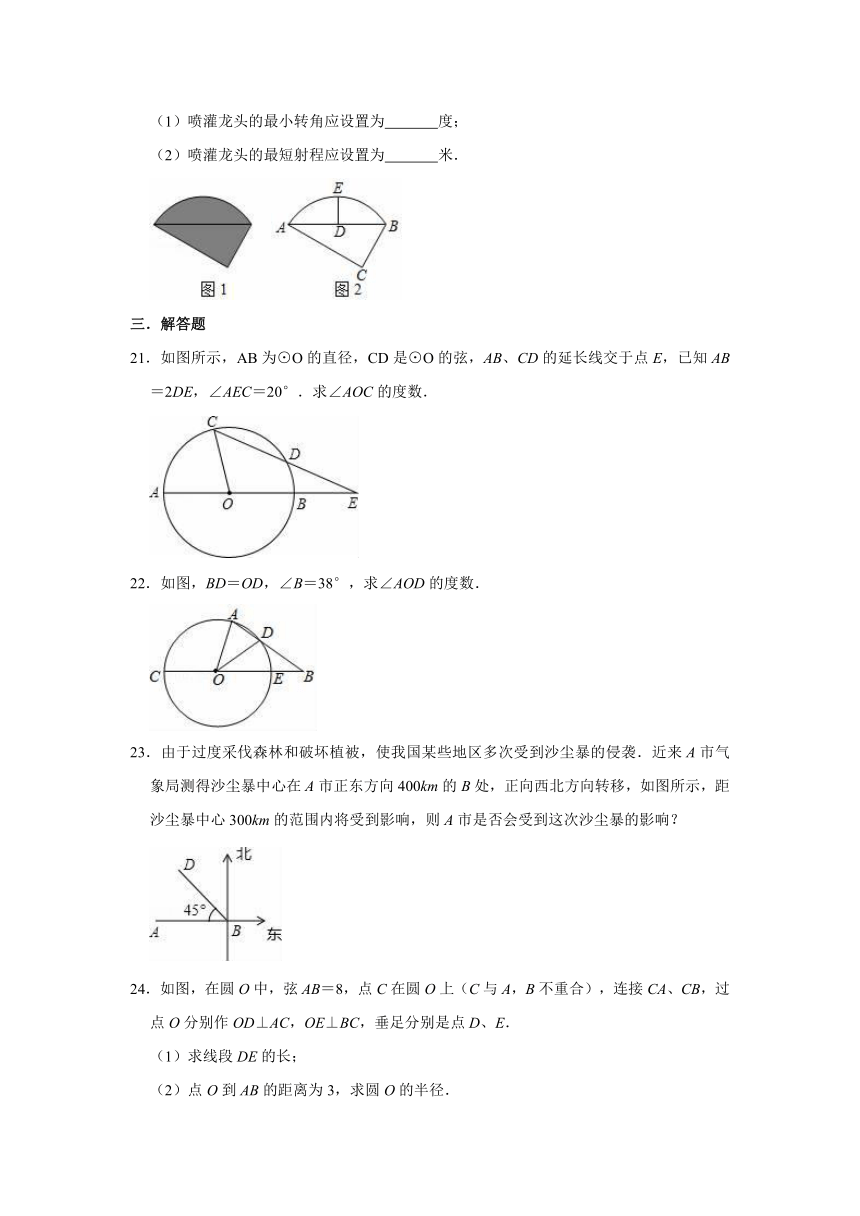
21.如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
22.如图,BD=OD,∠B=38°,求∠AOD的度数.
23.由于过度采伐森林和破坏植被,使我国某些地区多次受到沙尘暴的侵袭.近来A市气象局测得沙尘暴中心在A市正东方向400km的B处,正向西北方向转移,如图所示,距沙尘暴中心300km的范围内将受到影响,则A市是否会受到这次沙尘暴的影响?
24.如图,在圆O中,弦AB=8,点C在圆O上(C与A,B不重合),连接CA、CB,过点O分别作OD⊥AC,OE⊥BC,垂足分别是点D、E.
(1)求线段DE的长;
(2)点O到AB的距离为3,求圆O的半径.
25.如图,小虎牵着小狗上街,小虎的手臂与绳长共为2.5
m(手臂与拉直的绳子在一条直线上)手臂肩部距地面1.5
m.当小虎站立不动时,小狗在平整的地面上活动的最大区域是多少?并画出平面图.
26.⊙O中,直径AB和弦CD相交于点E,已知AE=1cm,EB=5cm,且∠DEB=60°,求CD的长.
27.如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
(1)求圆弧所在的圆的半径r的长;
(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?
参考答案与试题解析
一.选择题
1.解:如图,过点O作OC⊥AB,垂足为C,
∵∠AOB=90°,∠A=∠AOC=45°,
∴OC=AC,
∵CO=4,
∴AC=4,
∴OA=4,
∴⊙O的直径长为8.
故选:B.
2.解:∵OA==3,
∴OA=⊙O半径,
∴点A与⊙O的位置关系为:点在圆上.
故选:B.
3.解:∵圆心确定,半径确定后才可以确定圆,
∴D选项正确,
故选:D.
4.解:直径是弦,A正确,不符合题意;
在同圆或等圆中,相等的圆心角所对的弧相等,B错误,符合题意;
弦的垂直平分线一定经过圆心,C正确,不符合题意;
平分弧的半径垂直于弧所对的弦,D正确,不符合题意;
故选:B.
5.解:∵直角△PAB中,AB2=PA2+PB2,
又∵矩形PAOB中,OP=AB,
∴PA2+PB2=AB2=OP2.
故选:C.
6.解:连接OA,
∵⊙O的直径CD=20,OM:OC=3:5,
∴OC=10,OM=6,
∵AB⊥CD,
∴AM===8,
∴AB=2AM=16.
故选:C.
7.解:如图,
连接OA,
∵⊙O的直径CD=12cm,
∴OD=OA=OC=6,
∵OE:OC=1:3,
∴OE=2,
∵AB⊥CD,
∴AB=2AE,∠OEA=90°,
在Rt△OAE中,AE===4,
∴AB=2AE=8cm.
故选:D.
8.解:过A作⊙O的直径,交⊙O于D.
在△OAB中,OA=OB,
则∠BOD=∠ABO+∠OAB=2×20°=40°,
同理可得:∠COD=∠ACO+∠OAC=2×30°=60°,
故∠BOC=∠BOD+∠COD=100°.
故选:A.
9.解:∵OC⊥AB,
∴AD=DB=20m,
在Rt△AOD中,OA2=OD2+AD2,
设半径为r得:r2=(r﹣10)2+202,
解得:r=25m,
∴这段弯路的半径为25m
故选:A.
10.解:A、不能确定.因为半径不确定,故不符合题意;
B、不能确定.因为圆心的位置不确定,故不符合题意;
C、能确定,给定一直径,则圆心和半径确定,所以可以确定一个圆,故符合题意;
D、不能确定,不在同一直线上三点可以确定一个圆.故不符合题意;
故选:C.
二.填空题
11.解:∵∠BOC=110°,∠BOC+∠AOC=180°,
∴∠AOC=70°,
∵AD∥OC,OD=OA,
∴∠D=∠A=70°,
∴∠AOD=180°﹣2∠A=40°.
故答案为:40.
12.解:∵点P到圆心O的距离为6cm,
∴d=6cm,
∵⊙O的直径为10cm,
∴r=5,
∴d>r,
∴点P在圆外,
故答案为:点P在圆外.
13.解:连接OC,
∵CD=4,OD=3,
在Rt△ODC中,
∴OC===5,
∴AB=2OC=10,
故答案为:10.
14.解:∵OD=OA,
∴∠D=∠A,
而∠AOD=50°,
∴∠A=(180°﹣50°)=65°,
又∵AD∥OC,
∴∠BOC=∠A=65°.
故答案为:65.
15.解:连接OF,作FG⊥AB于点G.
则EG=DF﹣AE=5﹣3=2cm.
设⊙O的半径是R,
则OF=R,OG=R﹣2.
在直角△OFG中,OF2=FG2+OG2,
即R2=(R﹣2)2+42,
解得:R=5.
则直径是10cm.
故答案是:10.
16.解:根据垂径定理的推论:弦的垂直平分线必过圆心,
可以作弦AB和BC的垂直平分线,交点即为圆心.
如图所示,则圆心是(2,1).
故答案为:(2,1).
17.解:分别作三角形的三边的垂直平分线,可知相交于点(6,2),
即△ABC中外接圆的圆心坐标是(6,2).
故答案为:(6,2).
18.解:作OH⊥CD于H,连接OC,如图,
∵OH⊥CD,
∴HC=HD,
∵AP=2,BP=6,
∴AB=8,
∴OA=4,
∴OP=OA﹣AP=2,
在Rt△OPH中,∵∠OPH=30°,
∴∠POH=60°,
∴OH=OP=1,
在Rt△OHC中,∵OC=4,OH=1,
∴CH=,
∴CD=2CH=2.
故答案为:2
19.解:由于AC和BC值固定,点P在弧AD上,而B是圆心,所以PB的长也是定值,
因此,只要AP的长为最大值,
∴当P的运动到D点时,AP最长,
∵弧AD是以等边三角形ABC一边AB为半径的四分之一圆周,
∴∠DBA=90°,
∴由勾股定理得AD的长为5,
∴周长为5×3+5=15+5.
故答案为:15+5.
20.解:(1)∵AB=24米,BC=12米,AC=12米,
∴BC2+AC2=122+(12)2=576=242=AB2,
∴∠ACB=90°,
∴喷灌龙头的最小转角应设置为90°;
(2)如图3,作射线ED交AC于点M
∵AD=DB,ED⊥AB,是劣弧,
∴所在圆的圆心在射线DC上,
假设圆心为O,半径为r,连接OA,则OA=r,OD=r﹣6,AD=AB=12,
在Rt△AOD中,r2=122+(r﹣6)2,
解得:r=7,
∴OD=,
过点C作CN⊥AB,垂足为N,
∵∠ACB=90°,AB=24,BC=12,
∴sin∠BAC=,
∴∠BAC=30°,
∴CN=AC=6,AN=18,BN=6,
∴DM=×AD=4,
∴OD<MD,
∴点O在△ACB内部,
∴连接CO并延长交于点F,则CF为草坪上的点到C点的最大距离,
∵在上任取一点异于点F的点G,连接GO,GC,
∴CF=OC+OF=OC+OG>CG,
即CF>CG,
过O作OH⊥CN,垂足为H,则OH=DN=6,CH=6﹣=5,
∴OC===,
∴CF=OC+r=7+(米),
答:喷灌龙头的射程至少为(7+)米,
故答案为:(1)90;(2)7+.
三.解答题
21.解:连接OD,如图,
∵AB=2DE,
而AB=2OD,
∴OD=DE,
∴∠DOE=∠E=20°,
∴∠CDO=∠DOE+∠E=40°,
而OC=OD,
∴∠C=∠ODC=40°,
∴∠AOC=∠C+∠E=60°.
22.解:∵BD=OD,∠B=38°,
∴∠DOB=∠B=38°,
∴∠ADO=∠DOB+∠B=2×38°=76°,
∵OA=OD,
∴∠A=∠ADO=76°,
∴∠AOD=180°﹣∠A﹣∠ADO=180°﹣76°﹣76°=28°.
23.解:过A作AC⊥BD于C,由题意得AB=400km,
∠DBA=45°,所以AC=BC.
在Rt△ABC中,设AC=BC=x.
由勾股定理,得AC2+BC2=AB2,所以x2+x2=4002,
所以AC=x=200≈282.8(km).
282.8km<300km.
所以A市将受到这次沙尘暴的影响.
24.解:(1)∵OD经过圆心O,OD⊥AC,
∴AD=DC,
同理:CE=EB,
∴DE是△ABC的中位线,
∴DE=AB,
∵AB=8,
∴DE=4.
(2)过点O作OH⊥AB,垂足为点H,OH=3,连接OA,
∵OH经过圆心O,
∴AH=BH=AB,
∵AB=8,
∴AH=4,
在Rt△AHO中,AH2+OH2=AO2,
∴AO=5,即圆O的半径为5.
25.解:由题意可知AB=2.5m,AC=1.5m,
小狗在地平面上环绕跑圆的半径为=2.0(m),
小狗活动的区域是以2.0m为半径的圆,如图.
26.解:作OP⊥CD于P,连接OD,
∴CP=PD,
∵AE=1,EB=5,
∴AB=6,
∴OE=2,
在Rt△OPE中,OP=OE?sin∠DEB=,
∴PD==,
∴CD=2PD=2(cm).
27.解:(1)连接OA,
由题意得:AD=AB=30(米),OD=(r﹣18)
在Rt△ADO中,由勾股定理得:r2=302+(r﹣18)2,
解得,r=34(米);
(2)连接OA′,
∵OE=OP﹣PE=30米,
∴在Rt△A′EO中,由勾股定理得:A′E2=A′O2﹣OE2,即:A′E2=342﹣302,
解得:A′E=16(米).
∴A′B′=32(米).
∵A′B′=32>30,
∴不需要采取紧急措施.
对称图形——圆》单元测试卷
一.选择题
1.在⊙O中,圆心角∠AOB=90°,点O到弦AB的距离为4,则⊙O的直径的长为( )
A.
B.
C.24
D.16
2.已知⊙O半径为3,A为线段PO的中点,则当OP=6时,点A与⊙O的位置关系为( )
A.点在圆内
B.点在圆上
C.点在圆外
D.不能确定
3.下列条件中,能确定圆的是( )
A.以已知点O为圆心
B.以1cm长为半径
C.经过已知点A,且半径为2cm
D.以点O为圆心,1cm为半径
4.下列语句,错误的是( )
A.直径是弦
B.相等的圆心角所对的弧相等
C.弦的垂直平分线一定经过圆心
D.平分弧的半径垂直于弧所对的弦
5.如图,四边形PAOB是扇形OMN的内接矩形,顶点P在弧MN上,且不与M,N重合,当P点在弧MN上移动时,矩形PAOB的形状、大小随之变化,则PA2+PB2的值( )
A.变大
B.变小
C.不变
D.不能确定
6.如图,⊙O的直径CD=20,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )
A.8
B.12
C.16
D.2
7.如图,⊙O的直径CD=12cm,AB是⊙O的弦,AB⊥CD,垂足为E,OE:OC=1:3,则AB的长为( )
A.2cm
B.4cm
C.6cm
D.8cm
8.如图,A,B,C是⊙O上的三点,AB,AC的圆心O的两侧,若∠ABO=20°,∠ACO=30°,则∠BOC的度数为( )
A.100°
B.110°
C.125°
D.130°
9.如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,AB=40m,点C是的中点,点D是AB的中点,且CD=10m,则这段弯路所在圆的半径为( )
A.25m
B.24m
C.30m
D.60m
10.给定下列图形可以确定一个圆的是( )
A.已知圆心
B.已知半径
C.已知直径
D.已知三个点
二.填空题
11.如图,AB是⊙O的直径,点C、D在⊙O上,∠BOC=110°,AD∥OC,则∠AOD=
.
12.在平面内,⊙O的直径为10cm,点P到圆心O的距离是6cm,则点P与⊙O的位置关系是
.
13.如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D,已知CD=4,OD=3,求AB的长是
.
14.如图,AB为⊙O直径,点C、D在⊙O上,已知∠AOD=50°,AD∥OC,则∠BOC=
度.
15.如图,矩形ABCD的边AB过⊙O的圆心,E、F分别为AB、CD与⊙O的交点,若AE=3cm,AD=4cm,DF=5cm,则⊙O的直径等于
.
16.如图,在平面直角坐标系中,点A,B,C都在格点上,过A,B,C三点作一圆弧,则圆心的坐标是
.
17.如图△ABC中外接圆的圆心坐标是
.
18.如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为
.
19.如图所示,弧AD是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧AD上任意一点,若AC=5,则四边形ACBP周长的最大值是
.
20.“美丽乡村“的建设行动,让我们的家园拥有了靓丽的风景.如图1,是某乡村一角的草坪,草坪是由一块弓形草地和一块三角形草地组成.为了更科学地管理草坪,现需要给草坪装上自动喷灌装置,并且用喷灌龙头浇水时,既要保证草坪的每个角落都能浇上水,又能最大化的节约水,于是选择了一种转角在0°~180°内(含180°)可以自由设定(按设定的转角可以往复转动喷灌)、射程长短也可以自主设定的喷灌龙头.如图2,已知弓形高DE=6米,弓形宽AB=24米.△ABC的边BC=12米,AC=12米.若经测算,将喷灌龙头安装在△ABC的顶点C时为最优方案,则:
(1)喷灌龙头的最小转角应设置为
度;
(2)喷灌龙头的最短射程应设置为
米.
三.解答题
21.如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
22.如图,BD=OD,∠B=38°,求∠AOD的度数.
23.由于过度采伐森林和破坏植被,使我国某些地区多次受到沙尘暴的侵袭.近来A市气象局测得沙尘暴中心在A市正东方向400km的B处,正向西北方向转移,如图所示,距沙尘暴中心300km的范围内将受到影响,则A市是否会受到这次沙尘暴的影响?
24.如图,在圆O中,弦AB=8,点C在圆O上(C与A,B不重合),连接CA、CB,过点O分别作OD⊥AC,OE⊥BC,垂足分别是点D、E.
(1)求线段DE的长;
(2)点O到AB的距离为3,求圆O的半径.
25.如图,小虎牵着小狗上街,小虎的手臂与绳长共为2.5
m(手臂与拉直的绳子在一条直线上)手臂肩部距地面1.5
m.当小虎站立不动时,小狗在平整的地面上活动的最大区域是多少?并画出平面图.
26.⊙O中,直径AB和弦CD相交于点E,已知AE=1cm,EB=5cm,且∠DEB=60°,求CD的长.
27.如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
(1)求圆弧所在的圆的半径r的长;
(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?
参考答案与试题解析
一.选择题
1.解:如图,过点O作OC⊥AB,垂足为C,
∵∠AOB=90°,∠A=∠AOC=45°,
∴OC=AC,
∵CO=4,
∴AC=4,
∴OA=4,
∴⊙O的直径长为8.
故选:B.
2.解:∵OA==3,
∴OA=⊙O半径,
∴点A与⊙O的位置关系为:点在圆上.
故选:B.
3.解:∵圆心确定,半径确定后才可以确定圆,
∴D选项正确,
故选:D.
4.解:直径是弦,A正确,不符合题意;
在同圆或等圆中,相等的圆心角所对的弧相等,B错误,符合题意;
弦的垂直平分线一定经过圆心,C正确,不符合题意;
平分弧的半径垂直于弧所对的弦,D正确,不符合题意;
故选:B.
5.解:∵直角△PAB中,AB2=PA2+PB2,
又∵矩形PAOB中,OP=AB,
∴PA2+PB2=AB2=OP2.
故选:C.
6.解:连接OA,
∵⊙O的直径CD=20,OM:OC=3:5,
∴OC=10,OM=6,
∵AB⊥CD,
∴AM===8,
∴AB=2AM=16.
故选:C.
7.解:如图,
连接OA,
∵⊙O的直径CD=12cm,
∴OD=OA=OC=6,
∵OE:OC=1:3,
∴OE=2,
∵AB⊥CD,
∴AB=2AE,∠OEA=90°,
在Rt△OAE中,AE===4,
∴AB=2AE=8cm.
故选:D.
8.解:过A作⊙O的直径,交⊙O于D.
在△OAB中,OA=OB,
则∠BOD=∠ABO+∠OAB=2×20°=40°,
同理可得:∠COD=∠ACO+∠OAC=2×30°=60°,
故∠BOC=∠BOD+∠COD=100°.
故选:A.
9.解:∵OC⊥AB,
∴AD=DB=20m,
在Rt△AOD中,OA2=OD2+AD2,
设半径为r得:r2=(r﹣10)2+202,
解得:r=25m,
∴这段弯路的半径为25m
故选:A.
10.解:A、不能确定.因为半径不确定,故不符合题意;
B、不能确定.因为圆心的位置不确定,故不符合题意;
C、能确定,给定一直径,则圆心和半径确定,所以可以确定一个圆,故符合题意;
D、不能确定,不在同一直线上三点可以确定一个圆.故不符合题意;
故选:C.
二.填空题
11.解:∵∠BOC=110°,∠BOC+∠AOC=180°,
∴∠AOC=70°,
∵AD∥OC,OD=OA,
∴∠D=∠A=70°,
∴∠AOD=180°﹣2∠A=40°.
故答案为:40.
12.解:∵点P到圆心O的距离为6cm,
∴d=6cm,
∵⊙O的直径为10cm,
∴r=5,
∴d>r,
∴点P在圆外,
故答案为:点P在圆外.
13.解:连接OC,
∵CD=4,OD=3,
在Rt△ODC中,
∴OC===5,
∴AB=2OC=10,
故答案为:10.
14.解:∵OD=OA,
∴∠D=∠A,
而∠AOD=50°,
∴∠A=(180°﹣50°)=65°,
又∵AD∥OC,
∴∠BOC=∠A=65°.
故答案为:65.
15.解:连接OF,作FG⊥AB于点G.
则EG=DF﹣AE=5﹣3=2cm.
设⊙O的半径是R,
则OF=R,OG=R﹣2.
在直角△OFG中,OF2=FG2+OG2,
即R2=(R﹣2)2+42,
解得:R=5.
则直径是10cm.
故答案是:10.
16.解:根据垂径定理的推论:弦的垂直平分线必过圆心,
可以作弦AB和BC的垂直平分线,交点即为圆心.
如图所示,则圆心是(2,1).
故答案为:(2,1).
17.解:分别作三角形的三边的垂直平分线,可知相交于点(6,2),
即△ABC中外接圆的圆心坐标是(6,2).
故答案为:(6,2).
18.解:作OH⊥CD于H,连接OC,如图,
∵OH⊥CD,
∴HC=HD,
∵AP=2,BP=6,
∴AB=8,
∴OA=4,
∴OP=OA﹣AP=2,
在Rt△OPH中,∵∠OPH=30°,
∴∠POH=60°,
∴OH=OP=1,
在Rt△OHC中,∵OC=4,OH=1,
∴CH=,
∴CD=2CH=2.
故答案为:2
19.解:由于AC和BC值固定,点P在弧AD上,而B是圆心,所以PB的长也是定值,
因此,只要AP的长为最大值,
∴当P的运动到D点时,AP最长,
∵弧AD是以等边三角形ABC一边AB为半径的四分之一圆周,
∴∠DBA=90°,
∴由勾股定理得AD的长为5,
∴周长为5×3+5=15+5.
故答案为:15+5.
20.解:(1)∵AB=24米,BC=12米,AC=12米,
∴BC2+AC2=122+(12)2=576=242=AB2,
∴∠ACB=90°,
∴喷灌龙头的最小转角应设置为90°;
(2)如图3,作射线ED交AC于点M
∵AD=DB,ED⊥AB,是劣弧,
∴所在圆的圆心在射线DC上,
假设圆心为O,半径为r,连接OA,则OA=r,OD=r﹣6,AD=AB=12,
在Rt△AOD中,r2=122+(r﹣6)2,
解得:r=7,
∴OD=,
过点C作CN⊥AB,垂足为N,
∵∠ACB=90°,AB=24,BC=12,
∴sin∠BAC=,
∴∠BAC=30°,
∴CN=AC=6,AN=18,BN=6,
∴DM=×AD=4,
∴OD<MD,
∴点O在△ACB内部,
∴连接CO并延长交于点F,则CF为草坪上的点到C点的最大距离,
∵在上任取一点异于点F的点G,连接GO,GC,
∴CF=OC+OF=OC+OG>CG,
即CF>CG,
过O作OH⊥CN,垂足为H,则OH=DN=6,CH=6﹣=5,
∴OC===,
∴CF=OC+r=7+(米),
答:喷灌龙头的射程至少为(7+)米,
故答案为:(1)90;(2)7+.
三.解答题
21.解:连接OD,如图,
∵AB=2DE,
而AB=2OD,
∴OD=DE,
∴∠DOE=∠E=20°,
∴∠CDO=∠DOE+∠E=40°,
而OC=OD,
∴∠C=∠ODC=40°,
∴∠AOC=∠C+∠E=60°.
22.解:∵BD=OD,∠B=38°,
∴∠DOB=∠B=38°,
∴∠ADO=∠DOB+∠B=2×38°=76°,
∵OA=OD,
∴∠A=∠ADO=76°,
∴∠AOD=180°﹣∠A﹣∠ADO=180°﹣76°﹣76°=28°.
23.解:过A作AC⊥BD于C,由题意得AB=400km,
∠DBA=45°,所以AC=BC.
在Rt△ABC中,设AC=BC=x.
由勾股定理,得AC2+BC2=AB2,所以x2+x2=4002,
所以AC=x=200≈282.8(km).
282.8km<300km.
所以A市将受到这次沙尘暴的影响.
24.解:(1)∵OD经过圆心O,OD⊥AC,
∴AD=DC,
同理:CE=EB,
∴DE是△ABC的中位线,
∴DE=AB,
∵AB=8,
∴DE=4.
(2)过点O作OH⊥AB,垂足为点H,OH=3,连接OA,
∵OH经过圆心O,
∴AH=BH=AB,
∵AB=8,
∴AH=4,
在Rt△AHO中,AH2+OH2=AO2,
∴AO=5,即圆O的半径为5.
25.解:由题意可知AB=2.5m,AC=1.5m,
小狗在地平面上环绕跑圆的半径为=2.0(m),
小狗活动的区域是以2.0m为半径的圆,如图.
26.解:作OP⊥CD于P,连接OD,
∴CP=PD,
∵AE=1,EB=5,
∴AB=6,
∴OE=2,
在Rt△OPE中,OP=OE?sin∠DEB=,
∴PD==,
∴CD=2PD=2(cm).
27.解:(1)连接OA,
由题意得:AD=AB=30(米),OD=(r﹣18)
在Rt△ADO中,由勾股定理得:r2=302+(r﹣18)2,
解得,r=34(米);
(2)连接OA′,
∵OE=OP﹣PE=30米,
∴在Rt△A′EO中,由勾股定理得:A′E2=A′O2﹣OE2,即:A′E2=342﹣302,
解得:A′E=16(米).
∴A′B′=32(米).
∵A′B′=32>30,
∴不需要采取紧急措施.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
