2020-2021学年高二上学期数学人教B版(2019)选择性必修第一册第二章《平面解析几何》2.1坐标法教学课件(共16张PPT)
文档属性
| 名称 | 2020-2021学年高二上学期数学人教B版(2019)选择性必修第一册第二章《平面解析几何》2.1坐标法教学课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-10 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
2.1坐标法
教材分析
本节课选自《2019人教
B版高中数学选择性必修第一册》第二章《平面解析几何》第一节,本节课主要学习坐标法。在初中学习数轴及平面直角坐标系的基础上,结合向量的相关知识,通过两点间距离公式及中点公式的推导,体会坐标法的初步运用,并在这一过程中,进一步体会数形结合的思想,形成用代数的方法解决几何问题的能力。坐标法不仅是研究几何问题的重要方法,而且是一种广泛应用于其他领域的重要数学方法。通过坐标系,把点和坐标、曲线和方程联系起来,实现了形和数的统一。
给定一个平面,选定原点建立平面直角坐标系后,平面内点的位置可以用坐标来刻画。此时,平面内的直线是否可以通过直线上点的坐标来刻画?平面内其他几何对象能否也用类似的方法来描述?这些都是本章我们要探讨的问题,利用点的坐标来刻画几何对象,研究几何对象的性质以及探讨几何对象之间的关系,是解析几何的内容。
章节导语
学习目标
1.理解实数与数轴上的点的一一对应关系.
2.掌握数轴上两点形成的向量的坐标及两点间的距离公式、中点坐标公式.
3.探索并掌握平面直角坐标系中两点间的距离公式和中点坐标公式.
4.通过对两点间距离和中点坐标公式的探索,进一步体会坐标法在解决几何问题中的优越性.
1.数轴上的基本公式
(1)数轴的定义
给定了原点、单位长度与正方向的直线是数轴,数轴上的点与实数是一一对应的.
(2)数轴上的基本公式
温故知新
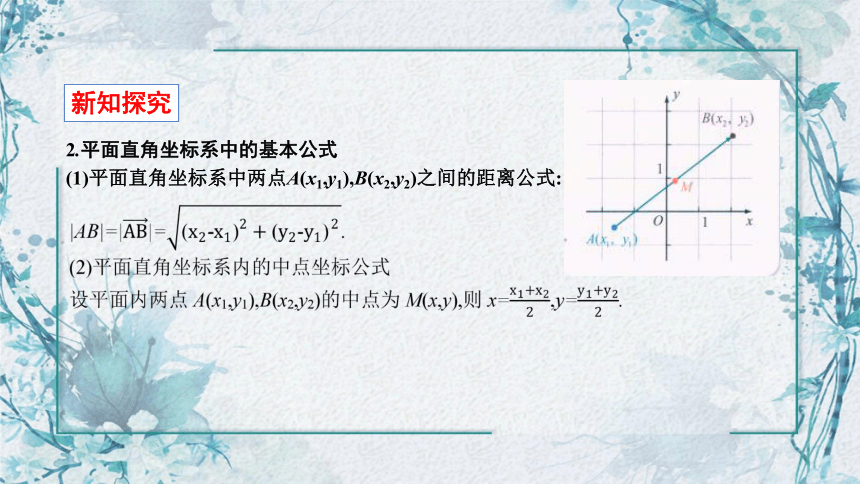
2.平面直角坐标系中的基本公式
(1)平面直角坐标系中两点A(x1,y1),B(x2,y2)之间的距离公式:
新知探究
说明:1.公式变形:
2.几何意义:两点的距离
3.两点间距离与A,B的顺序无关,仅与点的位置有关
4.距离公式是勾股定理的坐标形式;
公式应用
例1.
已知A(1,2),B(3,4),C(5,0)是△ABC的三个顶点,求这个三角形AB边上中线的长.
1.已知点A(4,12),在x轴上的点P与点A的距离等于13,求点P的坐标.
小试牛刀
解得x=9或x=-1.所以点P的坐标为(9,0)或(-1,0).
2.
P(x,y)关于G(x0,y0)的对称点的坐标是什么?
解析:P(x,y)关于G(x0,y0)的对称点的坐标为(2x0-x,2y0-y).
3.
已知A(1,3),B(5,2),点P在x轴上,则|AP|+|PB|的最小值为?
证明:取A为坐标原点,以AB
所在的直线为x轴,建立平面直角坐标系xOy,
依据平行四边形的性质
设点A,B,C,D
的坐标为
A(0,0),B(a,0),C(b,c),D(b-a,c),
已知□ABCD,求证:
坐标法
结论:平行四边形两条对角线的平方和等于它的四条边的平方和
所以
所以
即
方法总结
第一步:建立恰当的直角坐标系(避繁就简),设出点坐标.
第二步:列式,通过代数运算与变换,对数、代数式、方程等之间的关系进行讨论,解决代数问题
第三步:化简证明,把代数运算结果“翻译”成几何关系。
坐标法:在解决一些平面上的几何问题时,经常在平面上建立坐标系,以坐标系为桥梁,将几何问题转化为代数问题,通过代数运算研究几何图形的性质,这种方法称为坐标法.
如何选择坐标系:
1.将图形一边所在的直线或定直线作为x轴(或y轴);
2.对称图形,则取对称轴为x轴或y轴,若有直角,则取直角边所在直线
为坐标轴;
3.可将图形的一个定点或两个定点连线的中点作为原点.
例2.
已知四边形ABCD是一个长方形,AB=4,AD=1.判断线段CD上是否存在点P,使得AP?BP.如果存在,指出满足条件的P有多少个;如果不存在,说明理由.
归纳总结
数学思想方法
1.坐标法(几何与代数的转化)
2.数形结合
3.转化与化归
例
1.已知
A(1,2),B(3,4),C(5,0)是△ABC的三个顶点,求这个三角形
AB边上中线的长.
变式训练:
1.已知点
A(4,12),在
x轴上的点
P与点
A的距离等于
13,求点
P的坐标.
2.
P(x,y)关于
G(x0,y0)的对称点的坐标是什么?3.已知
A(1,3),B(5,2),点
P在
x轴上,则|AP|+|PB|的最小值为?
例
2.已知四边形
ABCD是一个长方形,AB=4,AD=1.判断线段
CD上是否存在点
P,使得
AP?BP.如果存在,指出满足条件的
P有多少个;如果不存在,说明理由.
课下作业:
2.1坐标法
教材分析
本节课选自《2019人教
B版高中数学选择性必修第一册》第二章《平面解析几何》第一节,本节课主要学习坐标法。在初中学习数轴及平面直角坐标系的基础上,结合向量的相关知识,通过两点间距离公式及中点公式的推导,体会坐标法的初步运用,并在这一过程中,进一步体会数形结合的思想,形成用代数的方法解决几何问题的能力。坐标法不仅是研究几何问题的重要方法,而且是一种广泛应用于其他领域的重要数学方法。通过坐标系,把点和坐标、曲线和方程联系起来,实现了形和数的统一。
给定一个平面,选定原点建立平面直角坐标系后,平面内点的位置可以用坐标来刻画。此时,平面内的直线是否可以通过直线上点的坐标来刻画?平面内其他几何对象能否也用类似的方法来描述?这些都是本章我们要探讨的问题,利用点的坐标来刻画几何对象,研究几何对象的性质以及探讨几何对象之间的关系,是解析几何的内容。
章节导语
学习目标
1.理解实数与数轴上的点的一一对应关系.
2.掌握数轴上两点形成的向量的坐标及两点间的距离公式、中点坐标公式.
3.探索并掌握平面直角坐标系中两点间的距离公式和中点坐标公式.
4.通过对两点间距离和中点坐标公式的探索,进一步体会坐标法在解决几何问题中的优越性.
1.数轴上的基本公式
(1)数轴的定义
给定了原点、单位长度与正方向的直线是数轴,数轴上的点与实数是一一对应的.
(2)数轴上的基本公式
温故知新
2.平面直角坐标系中的基本公式
(1)平面直角坐标系中两点A(x1,y1),B(x2,y2)之间的距离公式:
新知探究
说明:1.公式变形:
2.几何意义:两点的距离
3.两点间距离与A,B的顺序无关,仅与点的位置有关
4.距离公式是勾股定理的坐标形式;
公式应用
例1.
已知A(1,2),B(3,4),C(5,0)是△ABC的三个顶点,求这个三角形AB边上中线的长.
1.已知点A(4,12),在x轴上的点P与点A的距离等于13,求点P的坐标.
小试牛刀
解得x=9或x=-1.所以点P的坐标为(9,0)或(-1,0).
2.
P(x,y)关于G(x0,y0)的对称点的坐标是什么?
解析:P(x,y)关于G(x0,y0)的对称点的坐标为(2x0-x,2y0-y).
3.
已知A(1,3),B(5,2),点P在x轴上,则|AP|+|PB|的最小值为?
证明:取A为坐标原点,以AB
所在的直线为x轴,建立平面直角坐标系xOy,
依据平行四边形的性质
设点A,B,C,D
的坐标为
A(0,0),B(a,0),C(b,c),D(b-a,c),
已知□ABCD,求证:
坐标法
结论:平行四边形两条对角线的平方和等于它的四条边的平方和
所以
所以
即
方法总结
第一步:建立恰当的直角坐标系(避繁就简),设出点坐标.
第二步:列式,通过代数运算与变换,对数、代数式、方程等之间的关系进行讨论,解决代数问题
第三步:化简证明,把代数运算结果“翻译”成几何关系。
坐标法:在解决一些平面上的几何问题时,经常在平面上建立坐标系,以坐标系为桥梁,将几何问题转化为代数问题,通过代数运算研究几何图形的性质,这种方法称为坐标法.
如何选择坐标系:
1.将图形一边所在的直线或定直线作为x轴(或y轴);
2.对称图形,则取对称轴为x轴或y轴,若有直角,则取直角边所在直线
为坐标轴;
3.可将图形的一个定点或两个定点连线的中点作为原点.
例2.
已知四边形ABCD是一个长方形,AB=4,AD=1.判断线段CD上是否存在点P,使得AP?BP.如果存在,指出满足条件的P有多少个;如果不存在,说明理由.
归纳总结
数学思想方法
1.坐标法(几何与代数的转化)
2.数形结合
3.转化与化归
例
1.已知
A(1,2),B(3,4),C(5,0)是△ABC的三个顶点,求这个三角形
AB边上中线的长.
变式训练:
1.已知点
A(4,12),在
x轴上的点
P与点
A的距离等于
13,求点
P的坐标.
2.
P(x,y)关于
G(x0,y0)的对称点的坐标是什么?3.已知
A(1,3),B(5,2),点
P在
x轴上,则|AP|+|PB|的最小值为?
例
2.已知四边形
ABCD是一个长方形,AB=4,AD=1.判断线段
CD上是否存在点
P,使得
AP?BP.如果存在,指出满足条件的
P有多少个;如果不存在,说明理由.
课下作业:
