人教版八上高分笔记之导与练12.2.4用HL判断三角形全等(原卷+答案)
文档属性
| 名称 | 人教版八上高分笔记之导与练12.2.4用HL判断三角形全等(原卷+答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-09 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
12.2全等三角形的判定
用HL判定两个直角三角形全等
知识要点:
斜边和??
??分别相等的两个直角三角形全等,简写成?
??或??
2.两直角边对应相等的两个直角三角形?
依据是??
3.有一锐角和一直角边或斜边对应相等的两个直角三角形??
??,依据是??
或?
?
易错点睛:
如图,∠A=∠D=90°,AB=CD,BE=CF,求证:ΔABF≌ΔDCE.
【点睛】①误把BE=CF看作两三角形对应边;②误把HL用作SAS.
典型例题:
题型一
用”HL”判定两个直角三角形全等
例1
如图,在RtΔABC中,∠ACB=90°,CA=CB,D是AC上一点,点E在BC的延长,且AE=BD,BD的延长线与AE相交于点F.试猜想BF与AE有何特殊的位置关系,并说明理由.
变式练习:
1、如图,已知AD,AF分别是钝角三角形ABC和钝角三角形ABE的高,且AD=AF,AC=AE.求证:BC=BE.
题型二
用其他方法判定两个直角三角形全等
如图,在ΔABC中,AD为边BC上的中线,分别过点C,B作直线AD的垂线,垂足分别为E,F.求证:BF=CE.
知识点睛
对于证明两个直角三角形全等,一般三角形全等的判定方法“SSS”“SAS”“ASA”“AAS”同样适用,要根据所给条件灵活选用适当的方法.
变式练习:
[教材P42例5变式题]如图,AC⊥BC,AD⊥BD,AD=BC,CE⊥AB,DF⊥AB,垂足分别为E,F.求证:CE=DF.
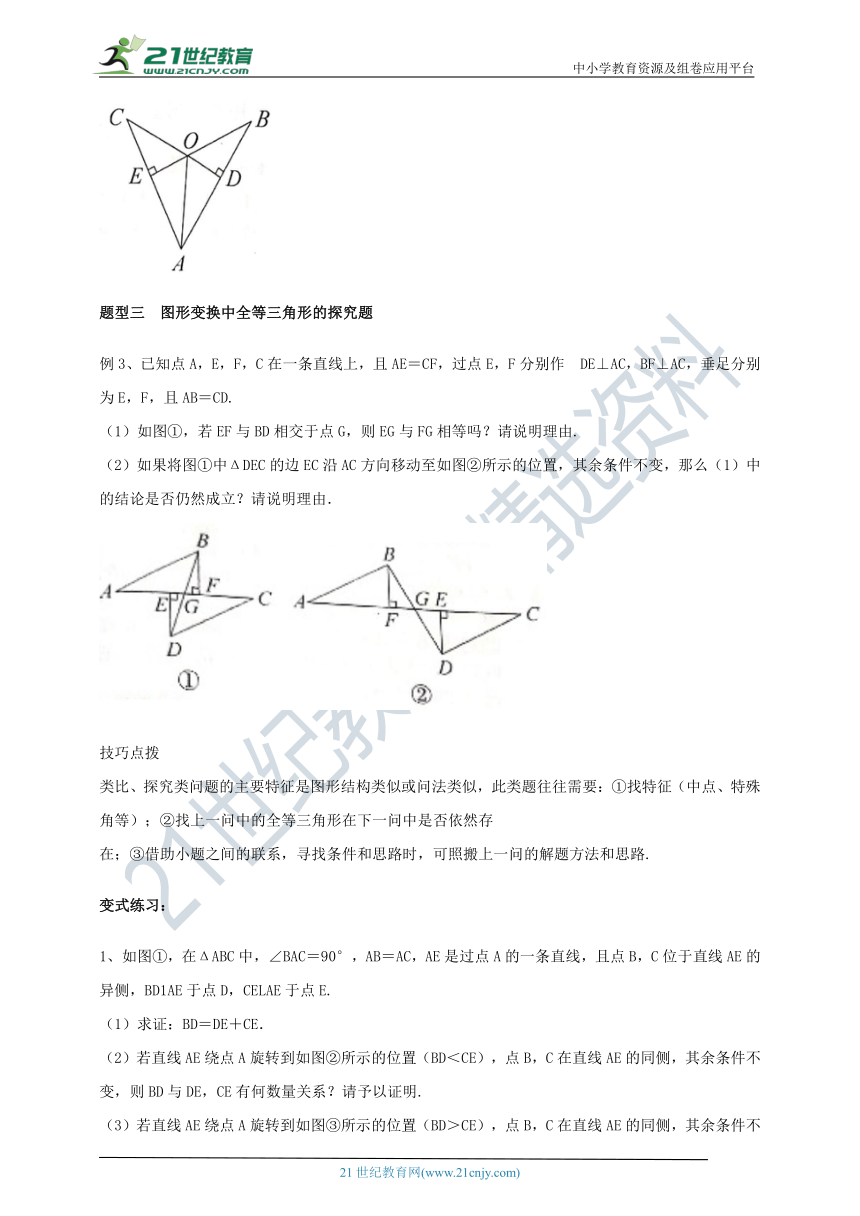
2、如图,CD⊥AB于点D,BE⊥AC于点E,BE,CD相交于点0,且AB=AC,连接AO.
(1)图中共有几对全等三角形?请一一列出.
(2)请选择一对全等三角形进行证明.
题型三
图形变换中全等三角形的探究题
例3、已知点A,E,F,C在一条直线上,且AE=CF,过点E,F分别作?DE⊥AC,BF⊥AC,垂足分别为E,F,且AB=CD.
(1)如图①,若EF与BD相交于点G,则EG与FG相等吗?请说明理由.
(2)如果将图①中ΔDEC的边EC沿AC方向移动至如图②所示的位置,其余条件不变,那么(1)中的结论是否仍然成立?请说明理由.
技巧点拨
类比、探究类问题的主要特征是图形结构类似或问法类似,此类题往往需要:①找特征(中点、特殊角等);②找上一问中的全等三角形在下一问中是否依然存
在;③借助小题之间的联系,寻找条件和思路时,可照搬上一问的解题方法和思路.
变式练习:
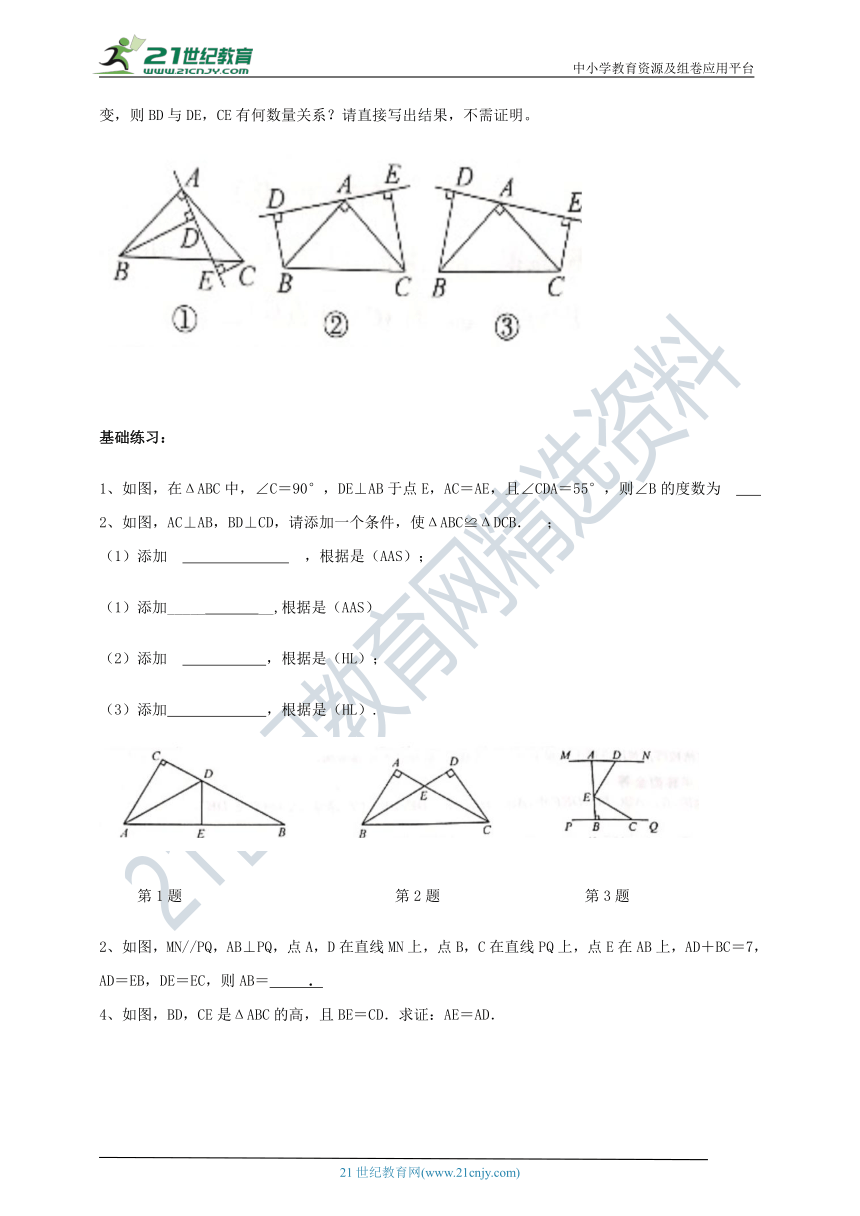
如图①,在ΔABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且点B,C位于直线AE的异侧,BD1AE于点D,CELAE于点E.
(1)求证:BD=DE+CE.
(2)若直线AE绕点A旋转到如图②所示的位置(BD<CE),点B,C在直线AE的同侧,其余条件不变,则BD与DE,CE有何数量关系?请予以证明.
(3)若直线AE绕点A旋转到如图③所示的位置(BD>CE),点B,C在直线AE的同侧,其余条件不变,则BD与DE,CE有何数量关系?请直接写出结果,不需证明。
基础练习:
如图,在ΔABC中,∠C=90°,DE⊥AB于点E,AC=AE,且∠CDA=55°,则∠B的度数为??
2、如图,AC⊥AB,BD⊥CD,请添加一个条件,使ΔABC≌ΔDCB.?;
(1)添加??
??,根据是(AAS);???
添加_____
__,根据是(AAS)
添加??
?,根据是(HL);
添加?
,根据是(HL).
第1题
第2题
第3题
如图,MN//PQ,AB⊥PQ,点A,D在直线MN上,点B,C在直线PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,则AB=
.
4、如图,BD,CE是ΔABC的高,且BE=CD.求证:AE=AD.
5、【教材变式】如图,在ΔABC中,D是AB的中点,DM⊥AC于点M,DN⊥BC于点N,且DM=DN.
(1)求证:AM=BN;
(2)求证:AC=BC.
综合探究
6、(1)【问题背景】如图1,已知∠ADB=∠AEC=90°,AD=AE,AB=AC.求证:EC=DB;
(2)【尝试应用】如图2,已知点A(2,2),点C在x轴正半轴上,点B在y轴的负半轴上,AB=AC.求OC-OB的值;
(3)【拓展创新】如图3,已知A(t,t),点D在x轴正半轴上,点B在y轴负半轴上,且∠ADB=∠ADx,直接写出OD+BD-OB的值为??
?(用含t的式子表示).
答案:
知识要点:
斜边和??一条直角边??分别相等的两个直角三角形全等,简写成?斜边、直角边??或??HL
2.两直角边对应相等的两个直角三角形?全等依据是??SAS
3.有一锐角和一直角边或斜边对应相等的两个直角三角形??全等??,依据是??AAS?或??ASA
易错点睛:
如图,∠A=∠D=90°,AB=CD,BE=CF,求证:ΔABF≌ΔDCE.
【点睛】①误把BE=CF看作两三角形对应边;②误把HL用作SAS.
证明略.
典型例题:
题型一
用”HL”判定两个直角三角形全等
例1
如图,在RtΔABC中,∠ACB=90°,CA=CB,D是AC上一点,点E在BC的延长,且AE=BD,BD的延长线与AE相交于点F.试猜想BF与AE有何特殊的位置关系,并说明理由.
解:猜想:BF⊥AE.理由:
∵∠ACB=90°,∴∠BCD=∠ACE=90°.
RtΔBDC≌RtΔAEC(HL)∴∠CBD=∠CAE.
∵∠CAE+∠E=90°,∴∠EBF+∠E=90°.
∴∠BFE=180°-∠EBF-∠E=180°-90°=90°,
∴BF⊥AE.
变式练习:
1、如图,已知AD,AF分别是钝角三角形ABC和钝角三角形ABE的高,且AD=AF,AC=AE.求证:BC=BE.
证明:∵AD,AF分别是钝角三角形ABC和钝角三角形ABE的高,
∴∠ADC=∠AFE=90°.
在RtΔADC和RtΔAFE中,
AC=AE,?AD=AF,
∴RtΔADC≌RtΔAFE(HL)∴CD=EF.
在RtΔABD和RtΔABF中,
AB=AB,?
AD=AF,
∴RtΔABD≌RtΔABF(HL)∴BD=BF.
∴BD-CD=BF-EF,即BC=BE.
题型二
用其他方法判定两个直角三角形全等
如图,在ΔABC中,AD为边BC上的中线,分别过点C,B作直线AD的
垂线,垂足分别为E,F.求证:BF=CE.
证明:∵CE⊥AF,BF⊥AF,∴∠CED=∠BFD=90°.
∵AD为边BC上的中线,∴BD=CD.
在ΔBFD和ΔCED中,∠BFD=∠CED,?∠BDF=∠CDE,BD=CD,
∴ΔBFD≌ΔCED(AAS)∴BF=CE.
知识点睛
对于证明两个直角三角形全等,一般三角形全等的判定方法“SSS”“SAS”“ASA”“AAS”同样适用,要根据所给条件灵活选用适当的方法.
变式练习:
[教材P42例5变式题]如图,AC⊥BC,AD⊥BD,AD=BC,CE⊥AB,DF⊥AB,垂足分别为E,F.求证:CE=DF.
证明:根据ΔBCE≌ΔADF?易证CE=DF.(略)
2、如图,CD⊥AB于点D,BE⊥AC于点E,BE,CD相交于点0,且AB=AC,连接AO.
(1)图中共有几对全等三角形?请一一列出.
(2)请选择一对全等三角形进行证明.
解:(1)4对.分别是
ΔADC≌ΔAEB,?
ΔBOD≌ΔCOE,?
ΔADO≌ΔAEO,?
ΔAOB≌ΔAOC.?
(2)选证ΔADC≌ΔAEB.(略)
题型三
图形变换中全等三角形的探究题
例3、已知点A,E,F,C在一条直线上,且AE=CF,过点E,F分别作?DE⊥AC,BF⊥AC,垂足分别为E,F,且AB=CD.
(1)如图①,若EF与BD相交于点G,则EG与FG相等吗?请说明理由.
(2)如果将图①中ΔDEC的边EC沿AC方向移动至如图②所示的位置,其余条件不变,那么(1)中的结论是否仍然成立?请说明理由.
解:(1)EG=FG.理由:
∵AE=CF,∴AE+EF=CF+EF,即AF=CE.?
∵BF⊥AC,DE⊥AC,∴∠AFB=∠CED=90°.?
在RtΔABF和RtΔCDE中,
AB=CD,?
AF=CE,?
∴RtΔABF≌RtΔCDE(HL)∴BF=DE.?
在ΔDEG和ΔBFG中,∠DGE=∠BGF,?∠DEG=∠BFG,?DE=BF,?
∴ΔDEG≌ΔBFG(AAS)∴EG=FG.?
(2)当ΔDEC的边EC沿AC方向移动至如图②所示的位置时,仍有EG=FG.理由:
∵AE=CF,∴AE-EF=CF-EF,即AF=CE.
同(1),可得EG=FG.
技巧点拨
类比、探究类问题的主要特征是图形结构类似或问法类似,此类题往往需要:①找特征(中点、特殊角等);②找上一问中的全等三角形在下一问中是否依然存
在;③借助小题之间的联系,寻找条件和思路时,可照搬上一问的解题方法和思路.
变式练习:
如图①,在ΔABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且点B,C位于直线AE的异侧,BD1AE于点D,CELAE于点E.
(1)求证:BD=DE+CE.
(2)若直线AE绕点A旋转到如图②所示的位置(BD<CE),点B,C在直线AE的同侧,其余条件不变,则BD与DE,CE有何数量关系?请予以证明.
(3)若直线AE绕点A旋转到如图③所示的位置(BD>CE),点B,C在直线AE的同侧,其余条件不变,则BD与DE,CE有何数量关系?请直接写出结果,不需证明。
证明:∵BD⊥AE,CE⊥AE,
∴∠ADB=∠AEC=90°.∴∠ABD+∠BAD=90°.?
又∠BAC=90°∴∠CAE+∠BAD=90°.
∴∠ABD=∠CAE.?
在ΔABD和ΔCAE中,∠ADB=∠CEA,?∠ABD=∠CAE,?AB=CA,
∴ΔABD≌ΔCAE(AAS)∴BD=AE,AD=CE.
∵AE=AD+DE,∴BD=DE+CE.
(2)解:BD=DE-CE.证明如下
∵BD⊥AE,CE⊥AE,∴∠ADB=∠AEC=90°.
∴∠ABD+∠BAD=90°
又∠BAC=90°,∴∠CAE+∠BAD=900
∴∠ABD=∠CAE.
在△ADB和△CEA中:∠ADB=∠CEA,
∠ABD=∠CAE,AB=CA
∴△ADB≌△CEA(AAS)∴BD=AE,AD=CE
∴BD=AE=DE-AAD=DE-CE
解:BD=DE-CE
基础练习:
如图,在ΔABC中,∠C=90°,DE⊥AB于点E,AC=AE,且∠CDA=55°,则∠B的度数为??20
2、如图,AC⊥AB,BD⊥CD,请添加一个条件,使ΔABC≌ΔDCB.?;
(1)添加??∠ABC=∠DCB??,根据是(AAS);???
添加_____∠ACB=∠DBC__,根据是(AAS)
添加??AB=CD?,根据是(HL);
添加??AC=BD,根据是(HL).
第1题
第2题
第3题
如图,MN//PQ,AB⊥PQ,点A,D在直线MN上,点B,C在直线PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,则AB=7.
4、如图,BD,CE是ΔABC的高,且BE=CD.求证:AE=AD.
证明:∵BD.CE是ΔABC的高,
∴∠BEC=∠AEC=∠ADB=∠CDB=90°,
在RtΔBEC和RtΔCDB中,?BC=BC,?BE=CD,
∴RtΔBEC≌RtΔCDB(HL),?
∴.BD=CE?
在ΔABD与ΔAEC中,∠AEC=∠ADB,∠A=∠A,BD=CE,
∴ΔABD≌ΔACE(AAS)∴AD=AE.
5、【教材变式】如图,在ΔABC中,D是AB的中点,DM⊥AC于点M,DN⊥BC于点N,且DM=DN.
(1)求证:AM=BN;
(2)求证:AC=BC.
证明:(1)连接CD,先证ΔDAM≌ΔDBN(HL),∴AM=BN;
(2)再证ΔCDM≌ΔCDN(HL),∴CM=CN,∴AC=BC.
综合探究
6、(1)【问题背景】如图1,已知∠ADB=∠AEC=90°,AD=AE,AB=AC.求证:EC=DB;
(2)【尝试应用】如图2,已知点A(2,2),点C在x轴正半轴上,点B在y轴的负半轴上,AB=AC.求OC-OB的值;
(3)【拓展创新】如图3,已知A(t,t),点D在x轴正半轴上,点B在y轴负半轴上,且∠ADB=∠ADx,直接写出OD+BD-OB的值为??2t?(用含t的式子表示).
解:(1)在RtΔADB和RtΔAEC中,AB=AC,AD=AE,
∴RtΔADB≌RtΔAEC(HL),∴EC=BD;
(2)过点A作AM⊥x轴于点M.AN⊥y轴于点N,
∵A(2.2),∴∠ANB=∠AMC=90°,AN=AM=2,
∵AB=AC,由(1)知BN=MC,∴OC-OB=OM+MC-(BN-ON)=OM+ON=4;
(3)在OD延长线上截取DC=DB,连接AC,
在ΔADB与ΔADC中.AD=AD,∠ADC=∠ADB.BD=DC.∴ΔADB≌ΔADC.∴AB=AC,由(2)知OC-OB=20M=21,
∴OD+DB-OB=OD+DC-OB=OC-OB=2t.?
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
12.2全等三角形的判定
用HL判定两个直角三角形全等
知识要点:
斜边和??
??分别相等的两个直角三角形全等,简写成?
??或??
2.两直角边对应相等的两个直角三角形?
依据是??
3.有一锐角和一直角边或斜边对应相等的两个直角三角形??
??,依据是??
或?
?
易错点睛:
如图,∠A=∠D=90°,AB=CD,BE=CF,求证:ΔABF≌ΔDCE.
【点睛】①误把BE=CF看作两三角形对应边;②误把HL用作SAS.
典型例题:
题型一
用”HL”判定两个直角三角形全等
例1
如图,在RtΔABC中,∠ACB=90°,CA=CB,D是AC上一点,点E在BC的延长,且AE=BD,BD的延长线与AE相交于点F.试猜想BF与AE有何特殊的位置关系,并说明理由.
变式练习:
1、如图,已知AD,AF分别是钝角三角形ABC和钝角三角形ABE的高,且AD=AF,AC=AE.求证:BC=BE.
题型二
用其他方法判定两个直角三角形全等
如图,在ΔABC中,AD为边BC上的中线,分别过点C,B作直线AD的垂线,垂足分别为E,F.求证:BF=CE.
知识点睛
对于证明两个直角三角形全等,一般三角形全等的判定方法“SSS”“SAS”“ASA”“AAS”同样适用,要根据所给条件灵活选用适当的方法.
变式练习:
[教材P42例5变式题]如图,AC⊥BC,AD⊥BD,AD=BC,CE⊥AB,DF⊥AB,垂足分别为E,F.求证:CE=DF.
2、如图,CD⊥AB于点D,BE⊥AC于点E,BE,CD相交于点0,且AB=AC,连接AO.
(1)图中共有几对全等三角形?请一一列出.
(2)请选择一对全等三角形进行证明.
题型三
图形变换中全等三角形的探究题
例3、已知点A,E,F,C在一条直线上,且AE=CF,过点E,F分别作?DE⊥AC,BF⊥AC,垂足分别为E,F,且AB=CD.
(1)如图①,若EF与BD相交于点G,则EG与FG相等吗?请说明理由.
(2)如果将图①中ΔDEC的边EC沿AC方向移动至如图②所示的位置,其余条件不变,那么(1)中的结论是否仍然成立?请说明理由.
技巧点拨
类比、探究类问题的主要特征是图形结构类似或问法类似,此类题往往需要:①找特征(中点、特殊角等);②找上一问中的全等三角形在下一问中是否依然存
在;③借助小题之间的联系,寻找条件和思路时,可照搬上一问的解题方法和思路.
变式练习:
如图①,在ΔABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且点B,C位于直线AE的异侧,BD1AE于点D,CELAE于点E.
(1)求证:BD=DE+CE.
(2)若直线AE绕点A旋转到如图②所示的位置(BD<CE),点B,C在直线AE的同侧,其余条件不变,则BD与DE,CE有何数量关系?请予以证明.
(3)若直线AE绕点A旋转到如图③所示的位置(BD>CE),点B,C在直线AE的同侧,其余条件不变,则BD与DE,CE有何数量关系?请直接写出结果,不需证明。
基础练习:
如图,在ΔABC中,∠C=90°,DE⊥AB于点E,AC=AE,且∠CDA=55°,则∠B的度数为??
2、如图,AC⊥AB,BD⊥CD,请添加一个条件,使ΔABC≌ΔDCB.?;
(1)添加??
??,根据是(AAS);???
添加_____
__,根据是(AAS)
添加??
?,根据是(HL);
添加?
,根据是(HL).
第1题
第2题
第3题
如图,MN//PQ,AB⊥PQ,点A,D在直线MN上,点B,C在直线PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,则AB=
.
4、如图,BD,CE是ΔABC的高,且BE=CD.求证:AE=AD.
5、【教材变式】如图,在ΔABC中,D是AB的中点,DM⊥AC于点M,DN⊥BC于点N,且DM=DN.
(1)求证:AM=BN;
(2)求证:AC=BC.
综合探究
6、(1)【问题背景】如图1,已知∠ADB=∠AEC=90°,AD=AE,AB=AC.求证:EC=DB;
(2)【尝试应用】如图2,已知点A(2,2),点C在x轴正半轴上,点B在y轴的负半轴上,AB=AC.求OC-OB的值;
(3)【拓展创新】如图3,已知A(t,t),点D在x轴正半轴上,点B在y轴负半轴上,且∠ADB=∠ADx,直接写出OD+BD-OB的值为??
?(用含t的式子表示).
答案:
知识要点:
斜边和??一条直角边??分别相等的两个直角三角形全等,简写成?斜边、直角边??或??HL
2.两直角边对应相等的两个直角三角形?全等依据是??SAS
3.有一锐角和一直角边或斜边对应相等的两个直角三角形??全等??,依据是??AAS?或??ASA
易错点睛:
如图,∠A=∠D=90°,AB=CD,BE=CF,求证:ΔABF≌ΔDCE.
【点睛】①误把BE=CF看作两三角形对应边;②误把HL用作SAS.
证明略.
典型例题:
题型一
用”HL”判定两个直角三角形全等
例1
如图,在RtΔABC中,∠ACB=90°,CA=CB,D是AC上一点,点E在BC的延长,且AE=BD,BD的延长线与AE相交于点F.试猜想BF与AE有何特殊的位置关系,并说明理由.
解:猜想:BF⊥AE.理由:
∵∠ACB=90°,∴∠BCD=∠ACE=90°.
RtΔBDC≌RtΔAEC(HL)∴∠CBD=∠CAE.
∵∠CAE+∠E=90°,∴∠EBF+∠E=90°.
∴∠BFE=180°-∠EBF-∠E=180°-90°=90°,
∴BF⊥AE.
变式练习:
1、如图,已知AD,AF分别是钝角三角形ABC和钝角三角形ABE的高,且AD=AF,AC=AE.求证:BC=BE.
证明:∵AD,AF分别是钝角三角形ABC和钝角三角形ABE的高,
∴∠ADC=∠AFE=90°.
在RtΔADC和RtΔAFE中,
AC=AE,?AD=AF,
∴RtΔADC≌RtΔAFE(HL)∴CD=EF.
在RtΔABD和RtΔABF中,
AB=AB,?
AD=AF,
∴RtΔABD≌RtΔABF(HL)∴BD=BF.
∴BD-CD=BF-EF,即BC=BE.
题型二
用其他方法判定两个直角三角形全等
如图,在ΔABC中,AD为边BC上的中线,分别过点C,B作直线AD的
垂线,垂足分别为E,F.求证:BF=CE.
证明:∵CE⊥AF,BF⊥AF,∴∠CED=∠BFD=90°.
∵AD为边BC上的中线,∴BD=CD.
在ΔBFD和ΔCED中,∠BFD=∠CED,?∠BDF=∠CDE,BD=CD,
∴ΔBFD≌ΔCED(AAS)∴BF=CE.
知识点睛
对于证明两个直角三角形全等,一般三角形全等的判定方法“SSS”“SAS”“ASA”“AAS”同样适用,要根据所给条件灵活选用适当的方法.
变式练习:
[教材P42例5变式题]如图,AC⊥BC,AD⊥BD,AD=BC,CE⊥AB,DF⊥AB,垂足分别为E,F.求证:CE=DF.
证明:根据ΔBCE≌ΔADF?易证CE=DF.(略)
2、如图,CD⊥AB于点D,BE⊥AC于点E,BE,CD相交于点0,且AB=AC,连接AO.
(1)图中共有几对全等三角形?请一一列出.
(2)请选择一对全等三角形进行证明.
解:(1)4对.分别是
ΔADC≌ΔAEB,?
ΔBOD≌ΔCOE,?
ΔADO≌ΔAEO,?
ΔAOB≌ΔAOC.?
(2)选证ΔADC≌ΔAEB.(略)
题型三
图形变换中全等三角形的探究题
例3、已知点A,E,F,C在一条直线上,且AE=CF,过点E,F分别作?DE⊥AC,BF⊥AC,垂足分别为E,F,且AB=CD.
(1)如图①,若EF与BD相交于点G,则EG与FG相等吗?请说明理由.
(2)如果将图①中ΔDEC的边EC沿AC方向移动至如图②所示的位置,其余条件不变,那么(1)中的结论是否仍然成立?请说明理由.
解:(1)EG=FG.理由:
∵AE=CF,∴AE+EF=CF+EF,即AF=CE.?
∵BF⊥AC,DE⊥AC,∴∠AFB=∠CED=90°.?
在RtΔABF和RtΔCDE中,
AB=CD,?
AF=CE,?
∴RtΔABF≌RtΔCDE(HL)∴BF=DE.?
在ΔDEG和ΔBFG中,∠DGE=∠BGF,?∠DEG=∠BFG,?DE=BF,?
∴ΔDEG≌ΔBFG(AAS)∴EG=FG.?
(2)当ΔDEC的边EC沿AC方向移动至如图②所示的位置时,仍有EG=FG.理由:
∵AE=CF,∴AE-EF=CF-EF,即AF=CE.
同(1),可得EG=FG.
技巧点拨
类比、探究类问题的主要特征是图形结构类似或问法类似,此类题往往需要:①找特征(中点、特殊角等);②找上一问中的全等三角形在下一问中是否依然存
在;③借助小题之间的联系,寻找条件和思路时,可照搬上一问的解题方法和思路.
变式练习:
如图①,在ΔABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且点B,C位于直线AE的异侧,BD1AE于点D,CELAE于点E.
(1)求证:BD=DE+CE.
(2)若直线AE绕点A旋转到如图②所示的位置(BD<CE),点B,C在直线AE的同侧,其余条件不变,则BD与DE,CE有何数量关系?请予以证明.
(3)若直线AE绕点A旋转到如图③所示的位置(BD>CE),点B,C在直线AE的同侧,其余条件不变,则BD与DE,CE有何数量关系?请直接写出结果,不需证明。
证明:∵BD⊥AE,CE⊥AE,
∴∠ADB=∠AEC=90°.∴∠ABD+∠BAD=90°.?
又∠BAC=90°∴∠CAE+∠BAD=90°.
∴∠ABD=∠CAE.?
在ΔABD和ΔCAE中,∠ADB=∠CEA,?∠ABD=∠CAE,?AB=CA,
∴ΔABD≌ΔCAE(AAS)∴BD=AE,AD=CE.
∵AE=AD+DE,∴BD=DE+CE.
(2)解:BD=DE-CE.证明如下
∵BD⊥AE,CE⊥AE,∴∠ADB=∠AEC=90°.
∴∠ABD+∠BAD=90°
又∠BAC=90°,∴∠CAE+∠BAD=900
∴∠ABD=∠CAE.
在△ADB和△CEA中:∠ADB=∠CEA,
∠ABD=∠CAE,AB=CA
∴△ADB≌△CEA(AAS)∴BD=AE,AD=CE
∴BD=AE=DE-AAD=DE-CE
解:BD=DE-CE
基础练习:
如图,在ΔABC中,∠C=90°,DE⊥AB于点E,AC=AE,且∠CDA=55°,则∠B的度数为??20
2、如图,AC⊥AB,BD⊥CD,请添加一个条件,使ΔABC≌ΔDCB.?;
(1)添加??∠ABC=∠DCB??,根据是(AAS);???
添加_____∠ACB=∠DBC__,根据是(AAS)
添加??AB=CD?,根据是(HL);
添加??AC=BD,根据是(HL).
第1题
第2题
第3题
如图,MN//PQ,AB⊥PQ,点A,D在直线MN上,点B,C在直线PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,则AB=7.
4、如图,BD,CE是ΔABC的高,且BE=CD.求证:AE=AD.
证明:∵BD.CE是ΔABC的高,
∴∠BEC=∠AEC=∠ADB=∠CDB=90°,
在RtΔBEC和RtΔCDB中,?BC=BC,?BE=CD,
∴RtΔBEC≌RtΔCDB(HL),?
∴.BD=CE?
在ΔABD与ΔAEC中,∠AEC=∠ADB,∠A=∠A,BD=CE,
∴ΔABD≌ΔACE(AAS)∴AD=AE.
5、【教材变式】如图,在ΔABC中,D是AB的中点,DM⊥AC于点M,DN⊥BC于点N,且DM=DN.
(1)求证:AM=BN;
(2)求证:AC=BC.
证明:(1)连接CD,先证ΔDAM≌ΔDBN(HL),∴AM=BN;
(2)再证ΔCDM≌ΔCDN(HL),∴CM=CN,∴AC=BC.
综合探究
6、(1)【问题背景】如图1,已知∠ADB=∠AEC=90°,AD=AE,AB=AC.求证:EC=DB;
(2)【尝试应用】如图2,已知点A(2,2),点C在x轴正半轴上,点B在y轴的负半轴上,AB=AC.求OC-OB的值;
(3)【拓展创新】如图3,已知A(t,t),点D在x轴正半轴上,点B在y轴负半轴上,且∠ADB=∠ADx,直接写出OD+BD-OB的值为??2t?(用含t的式子表示).
解:(1)在RtΔADB和RtΔAEC中,AB=AC,AD=AE,
∴RtΔADB≌RtΔAEC(HL),∴EC=BD;
(2)过点A作AM⊥x轴于点M.AN⊥y轴于点N,
∵A(2.2),∴∠ANB=∠AMC=90°,AN=AM=2,
∵AB=AC,由(1)知BN=MC,∴OC-OB=OM+MC-(BN-ON)=OM+ON=4;
(3)在OD延长线上截取DC=DB,连接AC,
在ΔADB与ΔADC中.AD=AD,∠ADC=∠ADB.BD=DC.∴ΔADB≌ΔADC.∴AB=AC,由(2)知OC-OB=20M=21,
∴OD+DB-OB=OD+DC-OB=OC-OB=2t.?
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
