人教版八上高分笔记之导与练12.3.1角的平分线的性质(原卷+答案)
文档属性
| 名称 | 人教版八上高分笔记之导与练12.3.1角的平分线的性质(原卷+答案) |  | |
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-09 21:59:46 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
12.3角的平分线的性质
角的平分线的性质
知识要点:
角的平分线上的点到角的两边的??
?相等.
2.三角形三条??
??的交点到三边的距离相等.
3.如图,根据角平分线的性质填空:
∵∠1=∠2,AD⊥CD,AB⊥BC,∴
=
?
(2)∵∠3=∠4,CD⊥AD,CB⊥AB,∴??
??=??
?
易错点睛:
如图,AD平分∠EAF,过点D作BCLAD,分别交AE,AF于点B,C.求证:BD=DC.
证明:∵AD平分∠EAF,BD⊥AD,CD⊥AD,
∴BD=CD.?
请指出上述证明过程中的错误之处.
【点睛】?误把BD,CD当作点D到AE,AF两边的距离而出错。
典型例题:
题型一
与角的平分线有关的尺规作图
例1、如图①,在ΔABC中,∠B=∠C,D是BA延长线上一点,E是AC的中点.
(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母.(不写作法,保留作图痕迹)
①作∠DAC的平分线AM;
②连接BE并延长交AM于点F.
(2)猜想与证明:试猜想AF与BC有怎样的位置关系和数量关系,并说明理由,
技巧点拨:两条线段之间的关系有位置关系和数量关系两种.位置关系包括垂直、平行等,数量关系包括相等、和差倍分等.当题目条件中的等线段、等角较多时,可考虑利用全等三角形进行证明.
变式练习:
已知:∠AOB.求作:∠AOB的平分线.
作法:(1)以点0为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(2)分别以点M,N为圆心,大于为半径画弧,两弧在ZAOB的内部相交于点C.
(3)画射线OC,射线OC即为所求(如图).请你根据提供的材料回答下列问题.
这种作已知角的平分线的方法的依据是?
.(填序号)
①“SSS”?②“SAS”?③“AAS”?④“ASA”
(2)请你证明OC为∠AOB的平分线.
2、如图,AB//CD,以点A为圆心,小于AC的长为半径画弧,分别交AB,AC于E,F两点,再分别以点E,F为圆心,大于的长为半径画弧,两弧交于点P,作射线AP交CD于点M.
(1)若∠ACD=135°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:ΔACN≌ΔMCN.?
题型二??角的平分线的性质的应用
1.利用角的平分线的性质求线段长度
例2、如图,在ΔABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB于点?E.若ΔBDE的周长是4cm,求AB的长.
解题策略:已知三角形的周长求某条线段的长时,若没有其他条件可得线段长度,则考虑进行转化,将三角形三边的长转化为一条线段的长.
变式练习:
1、如图,在RtΔABC中,∠C=90°,利用尺规在BC,BA上分别截取BE,
BD,使BE=BD;分别以点D,E为圆心,大于DE的长为半径画弧,两弧在LCBA的内部相交于点F;作射线BF交AC于点G.若CG=1,P为AB上一动点,则GP的最小值为(
)
A.无法确定
B.
C.1???????????D.2?
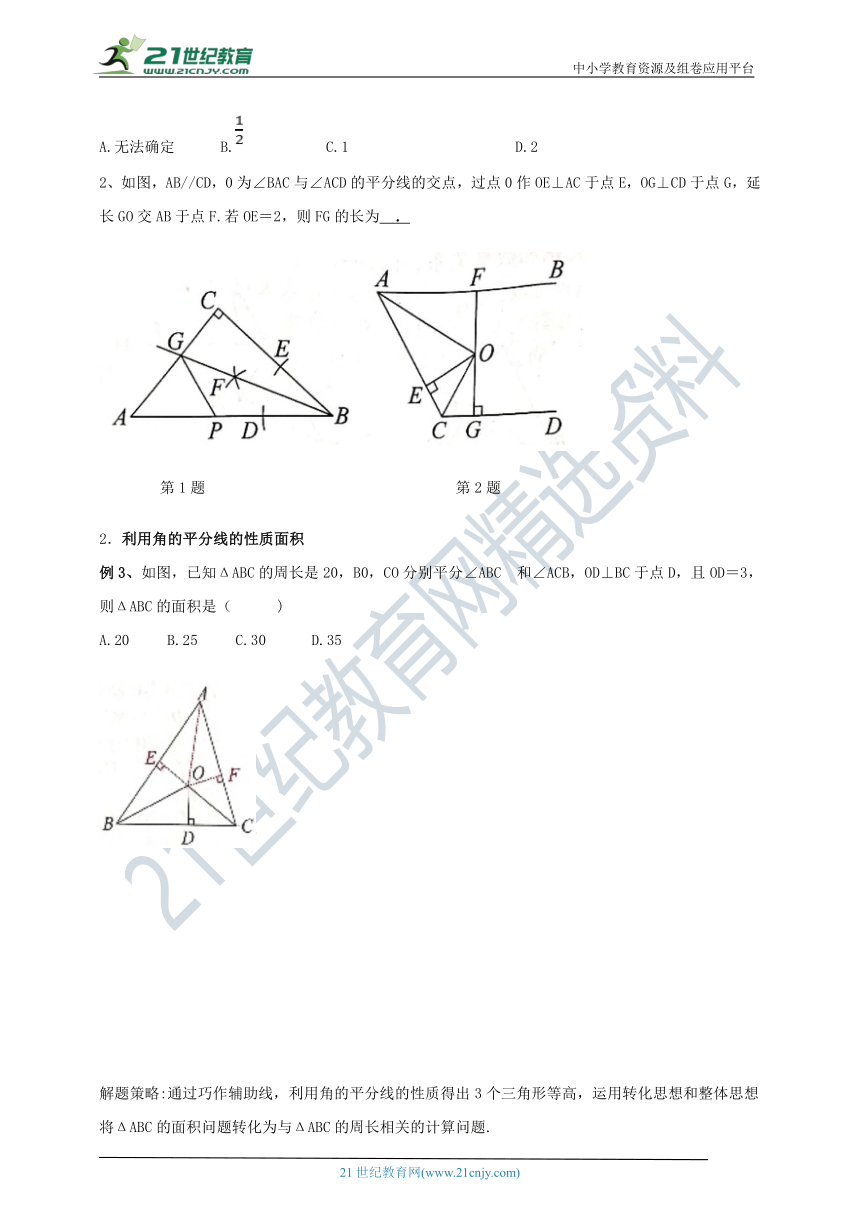
2、如图,AB//CD,0为∠BAC与∠ACD的平分线的交点,过点0作OE⊥AC于点E,OG⊥CD于点G,延长GO交AB于点F.若OE=2,则FG的长为
.
第1题
第2题
利用角的平分线的性质面积
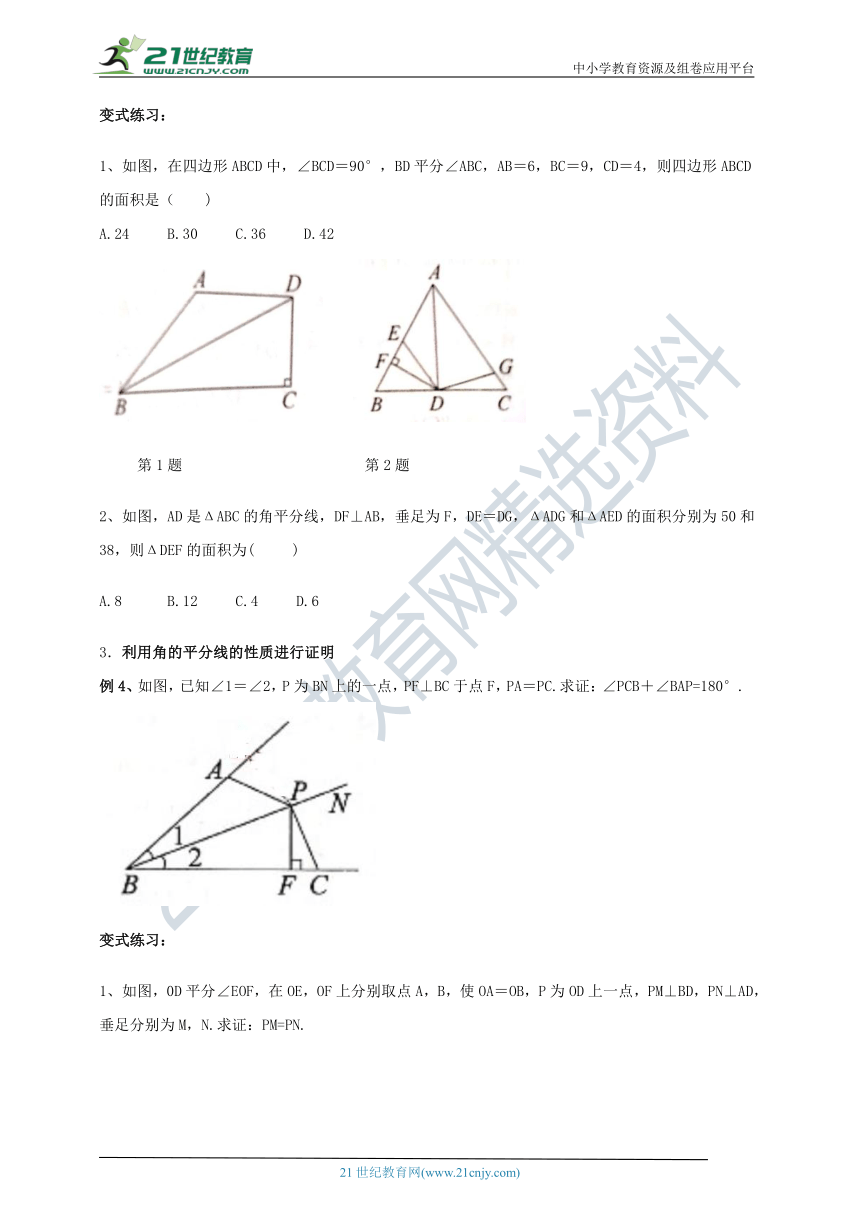
例3、如图,已知ΔABC的周长是20,B0,CO分别平分∠ABC?和∠ACB,OD⊥BC于点D,且OD=3,则ΔABC的面积是(?
)
A.20
B.25
C.30
D.35
解题策略:通过巧作辅助线,利用角的平分线的性质得出3个三角形等高,运用转化思想和整体思想将ΔABC的面积问题转化为与ΔABC的周长相关的计算问题.
变式练习:
如图,在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是(
?)
A.24
B.30
C.36
D.42
第1题
第2题
2、如图,AD是ΔABC的角平分线,DF⊥AB,垂足为F,DE=DG,ΔADG和ΔAED的面积分别为50和38,则ΔDEF的面积为(
)??
A.8
B.12
C.4
D.6
利用角的平分线的性质进行证明
例4、如图,已知∠1=∠2,P为BN上的一点,PF⊥BC于点F,PA=PC.求证:∠PCB+∠BAP=180°.?
变式练习:
如图,0D平分∠EOF,在OE,OF上分别取点A,B,使OA=OB,P为OD上一点,PM⊥BD,PN⊥AD,垂足分别为M,N.求证:PM=PN.?
2、如图,已知BF平分ΔABC的外角∠ABE,D为射线BF上一动点,AB与CD交于点P.若DA=DC,求证:∠ABC=∠ADC.
基础练习:
ΔABC的三边AB,BC,AC分别是6:4:4,点P为ΔABC三条角平分线的交点,则ΔABP,ΔBCP,ΔACP的面积比是??
2、如图,在ΔABC中,∠ACB=90°,AB=10,AC=8,CB=6,1是三条角平分线的交点,ID⊥BC于点D,则ID的长是___
__
第1题
第2题
第3题
3、如图,在RtΔABC中,∠C=90°,以点A为圆心,适当长为半径画弧,分别交AC,AB于点M.N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=3.AB=10,则ΔABD的面积是??
4、如图,在四边形ABCD中,∠B=∠D=90°,点E,F分别在AB,AD上,AE=AF,CE=CF.求证:CB=CD.
5、如图,在四边形ABCD中,∠B=90°,AB//CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.
(1)求证:AM⊥DM;
(2)求证:M为BC的中点.
综合题探究
6、(1)【感知】如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知BD、CD的数量关系为:?
(2)【探究】如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD=90°(1)中的结论是否仍然成立?请作出判断并给予证明。
(3)【应用】如图③,在四边形ABDC中,BD=CD,∠ABD+∠ACD=180°,∠ABD=90°,DE⊥AB,垂足为E.试判断AB,AC,BE的数量关系,并说明理由.
答案:
知识要点:
1.角的平分线上的点到角的两边的??距离??相等.
2.三角形三条??角平分线??的交点到三边的距离相等.
3.如图,根据角平分线的性质填空:
∵∠1=∠2,AD⊥CD,AB⊥BC,∴
AD
=
AB
?
(2)∵∠3=∠4,CD⊥AD,CB⊥AB,∴??CD??=??CB?
易错点睛:
如图,AD平分∠EAF,过点D作BCLAD,分别交AE,AF于点B,C.求证:BD=DC.
证明:∵AD平分∠EAF,BD⊥AD,CD⊥AD,
∴BD=CD.?
请指出上述证明过程中的错误之处.
【点睛】?误把BD,CD当作点D到AE,AF两边的距离而出错。
典型例题:
题型一
与角的平分线有关的尺规作图
例1、如图①,在ΔABC中,∠B=∠C,D是BA延长线上一点,E是AC的中点.
(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母.(不写作法,保留作图痕迹)
①作∠DAC的平分线AM;
②连接BE并延长交AM于点F.
(2)猜想与证明:试猜想AF与BC有怎样的位置关系和数量关系,并说明理由,
解:(1)如图②.
(2)AF//BC,AF=BC.理由:
∵∠ABC=∠C,∴∠DAC=∠ABC+∠C=2∠C.?
由作图可知∠DAC=2∠FAC,
∴∠C=∠FAC∴AF//BC.
∵E是AC的中点,∴AE=CE.
在ΔAEF和ΔCEB中,∠FAE=∠C,AE=CE,∠AEF=∠CEB,?
∴ΔAEF≌ΔCEB(ASA)∴AF=BC.
技巧点拨:两条线段之间的关系有位置关系和数量关系两种.位置关系包括垂直、平行等,数量关系包括相等、和差倍分等.当题目条件中的等线段、等角较多时,可考虑利用全等三角形进行证明.
变式练习:
已知:∠AOB.求作:∠AOB的平分线.
作法:(1)以点0为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(2)分别以点M,N为圆心,大于为半径画弧,两弧在ZAOB的内部相交于点C.
(3)画射线OC,射线OC即为所求(如图).请你根据提供的材料回答下列问题.
这种作已知角的平分线的方法的依据是?①.(填序号)
①“SSS”?②“SAS”?③“AAS”?④“ASA”
(2)请你证明OC为∠AOB的平分线.
解:由作图可知OM=ON,MC=NC.
在ΔOMC?和ΔONC中,
OM=ON,
OC=0C,
MC=NC,
∴ΔOMC≌ΔONC(SSS),∴∠MOC=∠NOC,
∴OC为∠AOB的平分线.
2、如图,AB//CD,以点A为圆心,小于AC的长为半径画弧,分别交AB,AC于E,F两点,再分别以点E,F为圆心,大于的长为半径画弧,两弧交于点P,作射线AP交CD于点M.
(1)若∠ACD=135°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:ΔACN≌ΔMCN.?
(1)解:∵AB//CD,
∴∠ACD+∠CAB=?180°?
又∠ACD=135°,
∴∠CAB=45°.
由作图可知,AM是∠CAB的平分线,
∴∠MAB=∠CAB=x45°=22.5°.
(2)证明:AM平分∠CAB,∴∠CAM=∠MAB.
∵AB//CD,∴∠MAB=∠CMA.∴∠CAM=∠CMA∴CN⊥AM,
∴∠ANC=∠MNC=90°.?
在ΔACN和ΔMCN中,?∠CAN=∠CMN,∠ANC=∠MNC,CN=CN,?
∴ΔACN≌ΔMCN(AAS).
题型二??角的平分线的性质的应用
1.利用角的平分线的性质求线段长度
例2、如图,在ΔABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB于点?E.若ΔBDE的周长是4cm,求AB的长.
解:∵∠C=90°,DE⊥AB,AD平分∠CAB,
∴∠C=∠DEA=90°,DC=DE.
在RtΔACD和RtΔAED中,
AD=AD,?
DC=DE,?
∴RtΔACD≌RtΔAED(HL).∴AC=AE.?
又AC=BC,∴AE=BC.∵ΔBDE的周长是4cm,
∴BD+DE+BE=BD+CD+BE=BC+BE=AE+BE=?AB=4cm,即AB=4?cm.?
解题策略:已知三角形的周长求某条线段的长时,若没有其他条件可得线段长度,则考虑进行转化,将三角形三边的长转化为一条线段的长.
变式练习:
1、如图,在RtΔABC中,∠C=90°,利用尺规在BC,BA上分别截取BE,
BD,使BE=BD;分别以点D,E为圆心,大于DE的长为半径画弧,两弧在LCBA的内部相交于点F;作射线BF交AC于点G.若CG=1,P为AB上一动点,则GP的最小值为(
C?
)
A.无法确定
B.
C.1???????????D.2?
2、如图,AB//CD,0为∠BAC与∠ACD的平分线的交点,过点0作OE⊥AC于点E,OG⊥CD于点G,延长GO交AB于点F.若OE=2,则FG的长为4.
第1题
第2题
利用角的平分线的性质面积
例3、如图,已知ΔABC的周长是20,B0,CO分别平分∠ABC?和∠ACB,OD⊥BC于点D,且OD=3,则ΔABC的面积是(?)
A.20
B.25
C.30
D.35
解析:如图,连接OA,过点0分别作OE⊥AB于点E,OF⊥AC于点F..
∵BO,CO分别平分∠ABC和∠ACB,OD⊥BC,∴OE=OF=OD=3.
∵ΔABC的周长是20,即AB+BC+AC=20,
∴SΔABC?=SΔAOB+S△BOC+S△AOC
=AB·OE+BC·0D+AC·OF
=0D·(AB+BC+AC)=x3x20=30.
答案:C
解题策略:通过巧作辅助线,利用角的平分线的性质得出3个三角形等高,运用转化思想和整体思想将ΔABC的面积问题转化为与ΔABC的周长相关的计算问题.
变式练习:
如图,在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是(
B?)
A.24
B.30
C.36
D.42
第1题
第2题
2、如图,AD是ΔABC的角平分线,DF⊥AB,垂足为F,DE=DG,ΔADG和ΔAED的面积分别为50和38,则ΔDEF的面积为(
D
)??
A.8
B.12
C.4
D.6
利用角的平分线的性质进行证明
例4、如图,已知∠1=∠2,P为BN上的一点,PF⊥BC于点F,PA=PC.求证:∠PCB+∠BAP=180°.?
证明:如图,过点P作PE⊥BA的延长线于点E.
∵∠1=∠2,PF⊥BC∴PE=PF.?
在RtΔAPE和RtΔCPF中,PA=PC,?PE=PF,?
∴RtΔAPE≌RtΔCPF(HL).
∴∠PAE=∠PCF.
∵∠PAE+∠BAP=180°,∴∠PCB+∠BAP=180°
解题策略:
上图中,∠1=∠2,AP=PC,∠PCB+∠BAP=180°,BF=(AB+BC)这四个条件可知二推二.
变式练习:
如图,0D平分∠EOF,在OE,OF上分别取点A,B,使OA=OB,P为OD上一点,PM⊥BD,PN⊥AD,垂足分别为M,N.求证:PM=PN.?
证明:∵OD平分∠EOF,
∴∠BOD=∠AOD.
在ΔBOD和ΔAOD?中:
OB=OA,?∠BOD=∠AOD,OD=0D,?
∴ΔBOD≌ΔAOD(SAS).?
∴∠BDO=∠ADO,即DO平分∠BDA.?
又P为DO上一点,且PM⊥BD,PN⊥AD,
∴PM=PN.?
2、如图,已知BF平分ΔABC的外角∠ABE,D为射线BF上一动点,AB与CD交于点P.若DA=DC,求证:∠ABC=∠ADC.
证明:如图,过点D分别作DM⊥BE于点M,DN⊥AB于点N.
又BF平分∠ABE,
∴DM=DN.
在RtΔCDM和RtΔADN中,
DC=DA,
DM=DN,
∴RtΔCDM≌RtΔADN(HL).
∴∠DCM=∠DAN.
∴∠DPB=∠ABC+∠DCM,∠APC=∠ADC+∠DAN,且∠DPB=∠APC,
∴∠ABC=∠ADC.
基础练习:
ΔABC的三边AB,BC,AC分别是6:4:4,点P为ΔABC三条角平分线的交点,则ΔABP,ΔBCP,ΔACP的面积比是??3:2:2
2、如图,在ΔABC中,∠ACB=90°,AB=10,AC=8,CB=6,1是三条角平分线的交点,ID⊥BC于点D,则ID的长是___2__
第1题
第2题
第3题
3、如图,在RtΔABC中,∠C=90°,以点A为圆心,适当长为半径画弧,分别交AC,AB于点M.N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=3.AB=10,则ΔABD的面积是??15
4、如图,在四边形ABCD中,∠B=∠D=90°,点E,F分别在AB,AD上,AE=AF,CE=CF.求证:CB=CD.
证明:连接AC,在ΔAEC和ΔAFC中,AE=AF,CE=CF.AC=AC
ΔAEC≌ΔAFC(SSS)
∴∠CAE=∠CAF
∵∠B=∠D=900
∴CB=CD
5、如图,在四边形ABCD中,∠B=90°,AB//CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.
(1)求证:AM⊥DM;(2)求证:M为BC的中点.
证明:(1)∵AB//CD.
∴∠BAD+∠ADC=180°.
∵AM平分∠BAD.DM平分/ADC,
∴2∠MAD+2∠ADM=180°.
∴∠MAD+∠ADM=90°,∴∠AMD=90°,即AM_DM;??
过点M作MNLAD交AD于点N,
∵∠B=90°,AB//CD,∴BM⊥AB,CM⊥CD,
∵AM平分∠BAD.DM平分∠ADC,
∴BM=MN.MN=CM·∵BM=CM,即M为BC的中点.
综合题探究
6、(1)【感知】如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知BD、CD的数量关系为:?BD=CD
(2)【探究】如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD=90°(1)中的结论是否仍然成立?请作出判断并给予证明。
(3)【应用】如图③,在四边形ABDC中,BD=CD,∠ABD+∠ACD=180°,∠ABD=90°?
DE⊥AB,垂足为E.试判断AB,AC,BE的数量关系,并说明理由.
解:(2)结论仍然成立,理由:如图②,过点D分别作DE⊥AB于点E,DF⊥AC
的延长线于点E
∵AD平分∠BAC,∴DE=DF.
∵∠ABD+∠ACD=180°,∠ACD+∠FCD=180°,?
∵∠ABD=∠FCD.?
在ΔDEB和ΔDFC中,∠EBD=∠FCD,∠DEB=∠F=90°,?DE=DF,?
∴ΔDEB≌ΔDFC(AAS),∴BD=CD.
(3)AB=AC+2BE.理由:如图③,过点D作DF⊥AC的延长线于点F,连接AD.
∵∠ABD+∠ACD=180°,∠ACD+∠FCD=180°.?
∴∠ABD=∠FCD.?
在ΔDEB和ΔDFC中?∠EBD=∠FCD,∠DEB=∠F=90°,?BD=CD,?
∴ΔDEB≌ΔDFC(AAS),
∴DE=DF.BE=CF.
在RtΔADF和RtΔADE中
AD=AD,
DF=DE,
RtΔADF≌RtΔADE(HL),
∴AF=AE,
∴AB=AE+BE=AF+BE=AC+CF+BE=AC+2BE.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
12.3角的平分线的性质
角的平分线的性质
知识要点:
角的平分线上的点到角的两边的??
?相等.
2.三角形三条??
??的交点到三边的距离相等.
3.如图,根据角平分线的性质填空:
∵∠1=∠2,AD⊥CD,AB⊥BC,∴
=
?
(2)∵∠3=∠4,CD⊥AD,CB⊥AB,∴??
??=??
?
易错点睛:
如图,AD平分∠EAF,过点D作BCLAD,分别交AE,AF于点B,C.求证:BD=DC.
证明:∵AD平分∠EAF,BD⊥AD,CD⊥AD,
∴BD=CD.?
请指出上述证明过程中的错误之处.
【点睛】?误把BD,CD当作点D到AE,AF两边的距离而出错。
典型例题:
题型一
与角的平分线有关的尺规作图
例1、如图①,在ΔABC中,∠B=∠C,D是BA延长线上一点,E是AC的中点.
(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母.(不写作法,保留作图痕迹)
①作∠DAC的平分线AM;
②连接BE并延长交AM于点F.
(2)猜想与证明:试猜想AF与BC有怎样的位置关系和数量关系,并说明理由,
技巧点拨:两条线段之间的关系有位置关系和数量关系两种.位置关系包括垂直、平行等,数量关系包括相等、和差倍分等.当题目条件中的等线段、等角较多时,可考虑利用全等三角形进行证明.
变式练习:
已知:∠AOB.求作:∠AOB的平分线.
作法:(1)以点0为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(2)分别以点M,N为圆心,大于为半径画弧,两弧在ZAOB的内部相交于点C.
(3)画射线OC,射线OC即为所求(如图).请你根据提供的材料回答下列问题.
这种作已知角的平分线的方法的依据是?
.(填序号)
①“SSS”?②“SAS”?③“AAS”?④“ASA”
(2)请你证明OC为∠AOB的平分线.
2、如图,AB//CD,以点A为圆心,小于AC的长为半径画弧,分别交AB,AC于E,F两点,再分别以点E,F为圆心,大于的长为半径画弧,两弧交于点P,作射线AP交CD于点M.
(1)若∠ACD=135°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:ΔACN≌ΔMCN.?
题型二??角的平分线的性质的应用
1.利用角的平分线的性质求线段长度
例2、如图,在ΔABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB于点?E.若ΔBDE的周长是4cm,求AB的长.
解题策略:已知三角形的周长求某条线段的长时,若没有其他条件可得线段长度,则考虑进行转化,将三角形三边的长转化为一条线段的长.
变式练习:
1、如图,在RtΔABC中,∠C=90°,利用尺规在BC,BA上分别截取BE,
BD,使BE=BD;分别以点D,E为圆心,大于DE的长为半径画弧,两弧在LCBA的内部相交于点F;作射线BF交AC于点G.若CG=1,P为AB上一动点,则GP的最小值为(
)
A.无法确定
B.
C.1???????????D.2?
2、如图,AB//CD,0为∠BAC与∠ACD的平分线的交点,过点0作OE⊥AC于点E,OG⊥CD于点G,延长GO交AB于点F.若OE=2,则FG的长为
.
第1题
第2题
利用角的平分线的性质面积
例3、如图,已知ΔABC的周长是20,B0,CO分别平分∠ABC?和∠ACB,OD⊥BC于点D,且OD=3,则ΔABC的面积是(?
)
A.20
B.25
C.30
D.35
解题策略:通过巧作辅助线,利用角的平分线的性质得出3个三角形等高,运用转化思想和整体思想将ΔABC的面积问题转化为与ΔABC的周长相关的计算问题.
变式练习:
如图,在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是(
?)
A.24
B.30
C.36
D.42
第1题
第2题
2、如图,AD是ΔABC的角平分线,DF⊥AB,垂足为F,DE=DG,ΔADG和ΔAED的面积分别为50和38,则ΔDEF的面积为(
)??
A.8
B.12
C.4
D.6
利用角的平分线的性质进行证明
例4、如图,已知∠1=∠2,P为BN上的一点,PF⊥BC于点F,PA=PC.求证:∠PCB+∠BAP=180°.?
变式练习:
如图,0D平分∠EOF,在OE,OF上分别取点A,B,使OA=OB,P为OD上一点,PM⊥BD,PN⊥AD,垂足分别为M,N.求证:PM=PN.?
2、如图,已知BF平分ΔABC的外角∠ABE,D为射线BF上一动点,AB与CD交于点P.若DA=DC,求证:∠ABC=∠ADC.
基础练习:
ΔABC的三边AB,BC,AC分别是6:4:4,点P为ΔABC三条角平分线的交点,则ΔABP,ΔBCP,ΔACP的面积比是??
2、如图,在ΔABC中,∠ACB=90°,AB=10,AC=8,CB=6,1是三条角平分线的交点,ID⊥BC于点D,则ID的长是___
__
第1题
第2题
第3题
3、如图,在RtΔABC中,∠C=90°,以点A为圆心,适当长为半径画弧,分别交AC,AB于点M.N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=3.AB=10,则ΔABD的面积是??
4、如图,在四边形ABCD中,∠B=∠D=90°,点E,F分别在AB,AD上,AE=AF,CE=CF.求证:CB=CD.
5、如图,在四边形ABCD中,∠B=90°,AB//CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.
(1)求证:AM⊥DM;
(2)求证:M为BC的中点.
综合题探究
6、(1)【感知】如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知BD、CD的数量关系为:?
(2)【探究】如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD=90°(1)中的结论是否仍然成立?请作出判断并给予证明。
(3)【应用】如图③,在四边形ABDC中,BD=CD,∠ABD+∠ACD=180°,∠ABD=90°,DE⊥AB,垂足为E.试判断AB,AC,BE的数量关系,并说明理由.
答案:
知识要点:
1.角的平分线上的点到角的两边的??距离??相等.
2.三角形三条??角平分线??的交点到三边的距离相等.
3.如图,根据角平分线的性质填空:
∵∠1=∠2,AD⊥CD,AB⊥BC,∴
AD
=
AB
?
(2)∵∠3=∠4,CD⊥AD,CB⊥AB,∴??CD??=??CB?
易错点睛:
如图,AD平分∠EAF,过点D作BCLAD,分别交AE,AF于点B,C.求证:BD=DC.
证明:∵AD平分∠EAF,BD⊥AD,CD⊥AD,
∴BD=CD.?
请指出上述证明过程中的错误之处.
【点睛】?误把BD,CD当作点D到AE,AF两边的距离而出错。
典型例题:
题型一
与角的平分线有关的尺规作图
例1、如图①,在ΔABC中,∠B=∠C,D是BA延长线上一点,E是AC的中点.
(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母.(不写作法,保留作图痕迹)
①作∠DAC的平分线AM;
②连接BE并延长交AM于点F.
(2)猜想与证明:试猜想AF与BC有怎样的位置关系和数量关系,并说明理由,
解:(1)如图②.
(2)AF//BC,AF=BC.理由:
∵∠ABC=∠C,∴∠DAC=∠ABC+∠C=2∠C.?
由作图可知∠DAC=2∠FAC,
∴∠C=∠FAC∴AF//BC.
∵E是AC的中点,∴AE=CE.
在ΔAEF和ΔCEB中,∠FAE=∠C,AE=CE,∠AEF=∠CEB,?
∴ΔAEF≌ΔCEB(ASA)∴AF=BC.
技巧点拨:两条线段之间的关系有位置关系和数量关系两种.位置关系包括垂直、平行等,数量关系包括相等、和差倍分等.当题目条件中的等线段、等角较多时,可考虑利用全等三角形进行证明.
变式练习:
已知:∠AOB.求作:∠AOB的平分线.
作法:(1)以点0为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(2)分别以点M,N为圆心,大于为半径画弧,两弧在ZAOB的内部相交于点C.
(3)画射线OC,射线OC即为所求(如图).请你根据提供的材料回答下列问题.
这种作已知角的平分线的方法的依据是?①.(填序号)
①“SSS”?②“SAS”?③“AAS”?④“ASA”
(2)请你证明OC为∠AOB的平分线.
解:由作图可知OM=ON,MC=NC.
在ΔOMC?和ΔONC中,
OM=ON,
OC=0C,
MC=NC,
∴ΔOMC≌ΔONC(SSS),∴∠MOC=∠NOC,
∴OC为∠AOB的平分线.
2、如图,AB//CD,以点A为圆心,小于AC的长为半径画弧,分别交AB,AC于E,F两点,再分别以点E,F为圆心,大于的长为半径画弧,两弧交于点P,作射线AP交CD于点M.
(1)若∠ACD=135°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:ΔACN≌ΔMCN.?
(1)解:∵AB//CD,
∴∠ACD+∠CAB=?180°?
又∠ACD=135°,
∴∠CAB=45°.
由作图可知,AM是∠CAB的平分线,
∴∠MAB=∠CAB=x45°=22.5°.
(2)证明:AM平分∠CAB,∴∠CAM=∠MAB.
∵AB//CD,∴∠MAB=∠CMA.∴∠CAM=∠CMA∴CN⊥AM,
∴∠ANC=∠MNC=90°.?
在ΔACN和ΔMCN中,?∠CAN=∠CMN,∠ANC=∠MNC,CN=CN,?
∴ΔACN≌ΔMCN(AAS).
题型二??角的平分线的性质的应用
1.利用角的平分线的性质求线段长度
例2、如图,在ΔABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB于点?E.若ΔBDE的周长是4cm,求AB的长.
解:∵∠C=90°,DE⊥AB,AD平分∠CAB,
∴∠C=∠DEA=90°,DC=DE.
在RtΔACD和RtΔAED中,
AD=AD,?
DC=DE,?
∴RtΔACD≌RtΔAED(HL).∴AC=AE.?
又AC=BC,∴AE=BC.∵ΔBDE的周长是4cm,
∴BD+DE+BE=BD+CD+BE=BC+BE=AE+BE=?AB=4cm,即AB=4?cm.?
解题策略:已知三角形的周长求某条线段的长时,若没有其他条件可得线段长度,则考虑进行转化,将三角形三边的长转化为一条线段的长.
变式练习:
1、如图,在RtΔABC中,∠C=90°,利用尺规在BC,BA上分别截取BE,
BD,使BE=BD;分别以点D,E为圆心,大于DE的长为半径画弧,两弧在LCBA的内部相交于点F;作射线BF交AC于点G.若CG=1,P为AB上一动点,则GP的最小值为(
C?
)
A.无法确定
B.
C.1???????????D.2?
2、如图,AB//CD,0为∠BAC与∠ACD的平分线的交点,过点0作OE⊥AC于点E,OG⊥CD于点G,延长GO交AB于点F.若OE=2,则FG的长为4.
第1题
第2题
利用角的平分线的性质面积
例3、如图,已知ΔABC的周长是20,B0,CO分别平分∠ABC?和∠ACB,OD⊥BC于点D,且OD=3,则ΔABC的面积是(?)
A.20
B.25
C.30
D.35
解析:如图,连接OA,过点0分别作OE⊥AB于点E,OF⊥AC于点F..
∵BO,CO分别平分∠ABC和∠ACB,OD⊥BC,∴OE=OF=OD=3.
∵ΔABC的周长是20,即AB+BC+AC=20,
∴SΔABC?=SΔAOB+S△BOC+S△AOC
=AB·OE+BC·0D+AC·OF
=0D·(AB+BC+AC)=x3x20=30.
答案:C
解题策略:通过巧作辅助线,利用角的平分线的性质得出3个三角形等高,运用转化思想和整体思想将ΔABC的面积问题转化为与ΔABC的周长相关的计算问题.
变式练习:
如图,在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是(
B?)
A.24
B.30
C.36
D.42
第1题
第2题
2、如图,AD是ΔABC的角平分线,DF⊥AB,垂足为F,DE=DG,ΔADG和ΔAED的面积分别为50和38,则ΔDEF的面积为(
D
)??
A.8
B.12
C.4
D.6
利用角的平分线的性质进行证明
例4、如图,已知∠1=∠2,P为BN上的一点,PF⊥BC于点F,PA=PC.求证:∠PCB+∠BAP=180°.?
证明:如图,过点P作PE⊥BA的延长线于点E.
∵∠1=∠2,PF⊥BC∴PE=PF.?
在RtΔAPE和RtΔCPF中,PA=PC,?PE=PF,?
∴RtΔAPE≌RtΔCPF(HL).
∴∠PAE=∠PCF.
∵∠PAE+∠BAP=180°,∴∠PCB+∠BAP=180°
解题策略:
上图中,∠1=∠2,AP=PC,∠PCB+∠BAP=180°,BF=(AB+BC)这四个条件可知二推二.
变式练习:
如图,0D平分∠EOF,在OE,OF上分别取点A,B,使OA=OB,P为OD上一点,PM⊥BD,PN⊥AD,垂足分别为M,N.求证:PM=PN.?
证明:∵OD平分∠EOF,
∴∠BOD=∠AOD.
在ΔBOD和ΔAOD?中:
OB=OA,?∠BOD=∠AOD,OD=0D,?
∴ΔBOD≌ΔAOD(SAS).?
∴∠BDO=∠ADO,即DO平分∠BDA.?
又P为DO上一点,且PM⊥BD,PN⊥AD,
∴PM=PN.?
2、如图,已知BF平分ΔABC的外角∠ABE,D为射线BF上一动点,AB与CD交于点P.若DA=DC,求证:∠ABC=∠ADC.
证明:如图,过点D分别作DM⊥BE于点M,DN⊥AB于点N.
又BF平分∠ABE,
∴DM=DN.
在RtΔCDM和RtΔADN中,
DC=DA,
DM=DN,
∴RtΔCDM≌RtΔADN(HL).
∴∠DCM=∠DAN.
∴∠DPB=∠ABC+∠DCM,∠APC=∠ADC+∠DAN,且∠DPB=∠APC,
∴∠ABC=∠ADC.
基础练习:
ΔABC的三边AB,BC,AC分别是6:4:4,点P为ΔABC三条角平分线的交点,则ΔABP,ΔBCP,ΔACP的面积比是??3:2:2
2、如图,在ΔABC中,∠ACB=90°,AB=10,AC=8,CB=6,1是三条角平分线的交点,ID⊥BC于点D,则ID的长是___2__
第1题
第2题
第3题
3、如图,在RtΔABC中,∠C=90°,以点A为圆心,适当长为半径画弧,分别交AC,AB于点M.N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=3.AB=10,则ΔABD的面积是??15
4、如图,在四边形ABCD中,∠B=∠D=90°,点E,F分别在AB,AD上,AE=AF,CE=CF.求证:CB=CD.
证明:连接AC,在ΔAEC和ΔAFC中,AE=AF,CE=CF.AC=AC
ΔAEC≌ΔAFC(SSS)
∴∠CAE=∠CAF
∵∠B=∠D=900
∴CB=CD
5、如图,在四边形ABCD中,∠B=90°,AB//CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.
(1)求证:AM⊥DM;(2)求证:M为BC的中点.
证明:(1)∵AB//CD.
∴∠BAD+∠ADC=180°.
∵AM平分∠BAD.DM平分/ADC,
∴2∠MAD+2∠ADM=180°.
∴∠MAD+∠ADM=90°,∴∠AMD=90°,即AM_DM;??
过点M作MNLAD交AD于点N,
∵∠B=90°,AB//CD,∴BM⊥AB,CM⊥CD,
∵AM平分∠BAD.DM平分∠ADC,
∴BM=MN.MN=CM·∵BM=CM,即M为BC的中点.
综合题探究
6、(1)【感知】如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知BD、CD的数量关系为:?BD=CD
(2)【探究】如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD=90°(1)中的结论是否仍然成立?请作出判断并给予证明。
(3)【应用】如图③,在四边形ABDC中,BD=CD,∠ABD+∠ACD=180°,∠ABD=90°?
DE⊥AB,垂足为E.试判断AB,AC,BE的数量关系,并说明理由.
解:(2)结论仍然成立,理由:如图②,过点D分别作DE⊥AB于点E,DF⊥AC
的延长线于点E
∵AD平分∠BAC,∴DE=DF.
∵∠ABD+∠ACD=180°,∠ACD+∠FCD=180°,?
∵∠ABD=∠FCD.?
在ΔDEB和ΔDFC中,∠EBD=∠FCD,∠DEB=∠F=90°,?DE=DF,?
∴ΔDEB≌ΔDFC(AAS),∴BD=CD.
(3)AB=AC+2BE.理由:如图③,过点D作DF⊥AC的延长线于点F,连接AD.
∵∠ABD+∠ACD=180°,∠ACD+∠FCD=180°.?
∴∠ABD=∠FCD.?
在ΔDEB和ΔDFC中?∠EBD=∠FCD,∠DEB=∠F=90°,?BD=CD,?
∴ΔDEB≌ΔDFC(AAS),
∴DE=DF.BE=CF.
在RtΔADF和RtΔADE中
AD=AD,
DF=DE,
RtΔADF≌RtΔADE(HL),
∴AF=AE,
∴AB=AE+BE=AF+BE=AC+CF+BE=AC+2BE.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
